Задача трёх узников
Задача трёх узников — парадокс теории вероятностей, имеющий общую природу с парадоксом Монти Холла. Этот парадокс впервые опубликовал Мартин Гарднер в 1959 году.
Формулировка
Трое заключённых, A, B и С заключены в одиночные камеры и приговорены к смертной казни. Губернатор случайным образом выбирает одного из них и милует его. Стражник, охраняющий заключённых, знает, кто помилован, но не имеет права сказать этого. Заключённый A просит стражника сказать ему имя того (другого) заключённого, кто точно будет казнён: «Если B помилован, скажи мне, что казнён будет C. Если помилован C, скажи мне, что казнён будет B. Если они оба будут казнены, а помилован я, подбрось монету, и скажи имя B или C».
Стражник говорит заключённому A, что заключённый B будет казнён. Заключённый A рад это слышать, поскольку он считает, что теперь вероятность его выживания стала 1/2, а не 1/3, как была до этого. Заключённый A тайно говорит заключённому С, что B будет казнен. Заключённый С также рад это слышать, поскольку он всё ещё полагает, что вероятность выживания заключённого А — 1/3, а его вероятность выживания возросла до 2/3. Как такое может быть?
Решение
Правильный ответ заключается в том, что заключённый A не получил информацию о своей собственной судьбе. Заключённый A до того, как спросить стражника, оценивает свои шансы как 1/3, так же как B и C. Когда стражник говорит, что B будет казнён, это всё равно, что вероятность того, что С помилован (вероятность 1/3) или A помилован (вероятность 1/3), и монета, выбиравшая между B и C, выбрала B. (Вероятность — 1/2; в целом вероятность того, что назван B — 1/6, поскольку A помилован). Поэтому, узнав, что B будет казнён, заключённый A оценивает шансы на помилование таким образом: его шансы теперь — 1/3, но теперь, зная, что B точно будет казнён, шансы С на помилование теперь 2/3.
Математическая формулировка
Обозначим A , B {\displaystyle A,B} и C {\displaystyle C} как события, означающие, что соответствующий заключённый будет помилован, и b {\displaystyle b} событие, означающее, что охранник назовёт имя B. Тогда, используя теорему Байеса вероятность помилования заключённого A:
P ( A ∣ b ) = P ( b ∣ A ) P ( A ) P ( b ∣ A ) P ( A ) + P ( b ∣ B ) P ( B ) + P ( b ∣ C ) P ( C ) = {\displaystyle P(A\mid b)={\frac {P(b\mid A)P(A)}{P(b\mid A)P(A)+P(b\mid B)P(B)+P(b\mid C)P(C)}}=} = 1 2 × 1 3 1 2 × 1 3 + 0 × 1 3 + 1 × 1 3 = 1 3 . {\displaystyle ={\frac {{\tfrac {1}{2}}\times {\tfrac {1}{3}}}{{\tfrac {1}{2}}\times {\tfrac {1}{3}}+0\times {\tfrac {1}{3}}+1\times {\tfrac {1}{3}}}}={\tfrac {1}{3}}.}Интуитивное решение
Заключённый A имеет шансы на помилование 1/3. Знание того, кто из B и C будет казнён, не меняет этого шанса. После того как заключённый А узнает, что B будет казнён, он осознаёт, что если он сам не помилован, то шанс того, что C будет помилован, теперь 2/3.
Материалы для понимания
Так же, как с проблемой Монти Холла, здесь будет полезно посмотреть на эту проблему с разных точек зрения.
Список возможных случаев
Могут возникнуть следующие случаи:
- A помилован, и стражник объявляет, что B будет казнён: 1/3×1/2=1/6 от всех случаев
- A помилован, и стражник объявляет, что C будет казнён: 1/3×1/2=1/6 от всех случаев
- B помилован, и стражник объявляет, что C будет казнён: 1/3 от всех случаев
- C помилован, и стражник объявляет, что B будет казнён: 1/3 от всех случаев
С оговоркой, что в ситуации когда А помилован (вероятность такой ситуации 1/3) стражник случайно выбирает имя казнённого, получается шанс 1/2, что он скажет «B» и 1/2 что он скажет «C». Это означает что вероятности: 1/6 в то время как (1/3 [А действительно помилован] * 1/2 [стражник называет B]), стражник называет B, потому что A помилован, и (1/3 [А действительно помилован] * 1/2 [стражник называет C]) стражник называет C, потому что A помилован. Всего это составляет 1/3 от всех случаев (1/6 + 1/6) когда А помилован.
Теперь ясно, что стражник отвечает «Казнён будет B» на вопрос заключенного А (это случаи 1 и 4) в 1/2 от всех случаев; 1/3 — вероятность того, что С помилован, но A всё равно будет казнён (случай 4); и только 1/6 — вероятность того, что A помилован (случай 1). Следовательно, шансы С: (1/3)/(1/2)=2/3, шансы A: (1/6)/(1/2)=1/3.
Основной загвоздкой здесь является то, что стражник не может говорить имя того, кто будет помилован. Если исключить это условие, исходную задачу можно переформулировать так: заключённый просит стражника сказать ему судьбу одного из двух заключённых B и С, не уточняя, кто будет казнён. В этом случае стражник подбрасывает монету, чтобы выбрать между B и С, и затем говорит судьбу одного из них. При такой формулировке возможны следующие случаи.
- A помилован, стражник говорит: B будет казнён (1/6)
- A помилован, стражник говорит: C будет казнён (1/6)
- B помилован, стражник говорит: B помилован (1/6)
- B помилован, стражник говорит: C будет казнён (1/6)
- C помилован, стражник говорит: B будет казнён (1/6)
- C помилован, стражник говорит: C помилован (1/6)
Все исходы имеют равную вероятность — 1/6. Итак: стражник в этой ситуации все равно выбирает из 6 случаев, и он всё ещё не может раскрыть карты и сказать, кто же помилован. В случае 3, стражник не может сказать, что B помилован, поэтому он скажет, что C будет казнён (что в общем-то будет правдой, ведь если помилован B, заключенные A и C будут казнены). Также и в случае 6, когда помилован C, но стражник, не имеющий права этого говорить, назовёт одного из тех, кто будет казнен — он назовёт заключённому А имя заключённого B. Это доводит вероятность случаев 4 и 5 до 1/3, что приводит нас к изначальным результатам.
В чём парадокс?
Люди думают, что вероятность 1/2, потому что они игнорируют суть вопроса, который заключённый A задаёт стражнику. Если бы стражник мог ответить на вопрос «Будет ли заключенный B казнен?», тогда в случае положительного ответа вероятность казни А действительно бы уменьшалась с 2/3 до 1/2.
То ограничение, которое есть в оригинальной задаче трёх узников, делает вопрос заключённого A бесполезным, ведь с вероятностью 100 % будут казнены два заключённых. То есть, даже если А помилован, ему назовут любое имя; если A приговорён к казни, то, значит, с ним вместе будет казнён ещё один заключённый, его имя и назовут заключённому А.
Получается, заключённый А своим вопросом просто узнаёт тот факт, что один из заключённых B и С будет казнён, что и так ясно из условий задачи.
Ссылки
- Mosteller, F. (англ.): Fifty Challenging Problems in Probability. Dover 1987 (reprint), ISBN 0-486-65355-2, p. 28-29 (restricted online version в «Книгах Google»)
- Richard Isaac: Pleasures of Probability. Springer 1995, ISBN 9780387944159, p. 24-27 (restricted online version в «Книгах Google»)
ru.wikipedia.org
1 − 2 + 3 − 4 + … это:
1 − 2 + 3 − 4 + … Первые 15000 частичных сумм ряда 0 + 1 − 2 + 3 − 4 + …
Первые 15000 частичных сумм ряда 0 + 1 − 2 + 3 − 4 + …
В математике, 1 − 2 + 3 − 4 + … — это числовой ряд, слагаемые которого по модулю представляют собой последовательные натуральные числа и имеют чередующийся знак. Частичная сумма с номером m этого ряда описывается выражением:
Такой числовой ряд расходится, то есть частичные суммы (1, −1, 2, −2, ...) не стремятся ни к какому конечному пределу. Тем не менее, в середине 18-го века Леонард Эйлер предложил выражение, которое он охарактеризовал как парадоксальное:
Математический аппарат, позволяющий интерпретировать это выражение, был разработан гораздо позже. Начиная с 1890 года, Чезаро, Борель и другие математики строго сформулировали методы получения обобщённых сумм расходящихся рядов, а также дополнили идеи Эйлера новыми интерпретациями. Многие из этих методов для суммы 1 − 2 + 3 − 4 + … дают результат, равный 1⁄4. Суммирование по Чезаро является одним из немногих методов, который не позволяет определить сумму 1 − 2 + 3 − 4 + …. Таким образом, чтобы получить конечную сумму обобщенным методом суммирования для этого ряда, требуется иной подход, например применение суммирования методом Абеля.
Ряд 1 − 2 + 3 − 4 + … тесно связан с рядом Гранди (1 − 1 + 1 − 1 + …). Эйлер трактовал эти ряды как два частных случая ряда 1 − 2n + 3n − 4n + …, который он изучал для произвольного n, работая над Базельской проблемой, и получил функциональные уравнения для функций, известных ныне как эта-функция Дирихле и дзета-функция Римана.
Содержание
|
Расходимость
Члены последовательности (1, −2, 3, −4, …) не стремятся к нулю, поэтому по необходимому условию сходимости рядов ряд 1 − 2 + 3 − 4 + … расходится. Для дальнейшего рассмотрения будет полезным более подробно рассмотреть расходимость этого ряда. По определению, сходимость или расходимость бесконечного ряда определяется сходимостью или расходимостью последовательности его частичных сумм, а частичными суммами ряда 1 − 2 + 3 − 4 + … являются[1]:8:
1 = 1, 1 − 2 = −1, 1 − 2 + 3 = 2, 1 − 2 + 3 − 4 = −2, 1 − 2 + 3 − 4 + 5 = 3, 1 − 2 + 3 − 4 + 5 − 6 = −3, …Эта последовательность замечательна тем, что в ней присутствует каждое целое число — даже ноль, если учитывать пустую частичную сумму — и таким образом множество значений членов этой последовательности счётно.[2]:23. Эта последовательность частичных сумм показывает, что ряд не сходится ни к какому конкретному числу (для любого x можно найти член, после которого все последующие частичные суммы будут находиться вне интервала [x-1, x+1]), и поэтому ряд 1 − 2 + 3 − 4 + … расходится.
Эвристика для суммирования
Стабильность и линейность
Поскольку члены 1, −2, 3, −4, 5, −6, … подчиняются простой закономерности, ряд 1 − 2 + 3 − 4 + … можно преобразовать сдвигом и почленным сложением с целью приписать ему некоторое числовое значение. Если выражение s = 1 − 2 + 3 − 4 + … для какого-то обычного числа s имеет смысл, то следующее формальное преобразование позволяет утверждать, что его значение в некотором смысле равно s = 1⁄4:[1]:6.
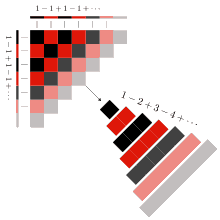
 При сложении четырёх копий 1 − 2 + 3 − 4 + …,, используя только сдвиги и почленное сложение, единица.
При сложении четырёх копий 1 − 2 + 3 − 4 + …,, используя только сдвиги и почленное сложение, единица.
Поэтому . Справа этот вывод проиллюстрирован графически.
Несмотря на то, что ряд 1 − 2 + 3 − 4 + … расходится и не имеет суммы в обычном смысле, выражение s = 1 − 2 + 3 − 4 + … = 1⁄4 даёт естественный ответ, если такая сумма может быть определена. Обобщённое определение «суммы» расходящегося ряда называется методом суммирования, который позволяет находить суммы для некоторого подмножества всех последовательностей. Существует множество методов обобщенного суммирования рядов (некоторые из них описаны ниже), которые обладают некоторыми свойствами обычного суммирования рядов. Выше было доказано следующее: если применить любой метод обобщенного суммирования, являющийся линейным и стабильным, который позволит получить сумму ряда 1 − 2 + 3 − 4 + …, то эта сумма составит 1⁄4. Более того, поскольку:
такой метод даст и сумму для ряда Гранди, которая будет равна 1 − 1 + 1 − 1 + … = 1⁄2.
Произведение Коши
В 1891 году Эрнесто Чезаро выразил надежду, что анализ расходящихся рядов выльется в исчисление, указывая: «Уже пишут (1 − 1 + 1 − 1 + …)2 = 1 − 2 + 3 − 4 + … и утверждают, что обе стороны равны 1⁄4.»[3]:130. Для Чезаро это выражение было применением теоремы, опубликованную им годом ранее, и которую можно считать первой теоремой в истории суммируемых расходящихся рядов. Детали этого метода суммирования изложены ниже; основная идея состоит в том, что 1 − 2 + 3 − 4 + … является произведением Коши 1 − 1 + 1 − 1 + … на 1 − 1 + 1 − 1 + ….
 1 − 2 + 3 − 4 + … как произведение Коши ряда 1 − 1 + 1 − 1 + … на самого себя
1 − 2 + 3 − 4 + … как произведение Коши ряда 1 − 1 + 1 − 1 + … на самого себя
Произведение Коши для двух бесконечных последовательностей определено даже если они обе расходятся. В случае, когда Σan = Σbn = Σ(−1)n, члены произведения Коши получаются из конечной диагональной суммы:
И тогда результирующая последовательность:
Поэтому метод суммирования, который сохраняет произведение Коши и даёт сумму 1 − 1 + 1 − 1 + … = 1⁄2,, также даст сумму 1 − 2 + 3 − 4 + … = 1⁄4. С использованием результатов, полученных в предыдущей секции, из этого вытекает эквивалентность суммируемости 1 − 1 + 1 − 1 + … и 1 − 2 + 3 − 4 + … при использовании методов суммирования, являющихся линейными, стабильными и сохраняющих произведение Коши.
Теорема Чезаро - это только пример. Ряд 1 − 1 + 1 − 1 + … является суммируемым по Чезаро в слабом смысле, и называется (C, 1)-суммируемым, в то время как 1 − 2 + 3 − 4 + … требует более сильной формы теоремы Чезаро[1]:3[4]:52-55 и называется (C, 2)-суммируемым. Поскольку все формы метода суммирования по Чезаро являются линейными и стабильными, значения сумм соответствуют вычисленным выше.
Частные методы
Метод Чезаро и Гёльдера
 Data about the (H, 2) sum of 1⁄4
Data about the (H, 2) sum of 1⁄4
Чтобы найти сумму по Чезаро (C, 1) для 1 − 2 + 3 − 4 + …, если она существует, нужно вычислить среднее арифметическое частичных сумм ряда. Частичные суммы таковы:
1, −1, 2, −2, 3, −3, …,и их среднее арифметическое составляет:
1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, ….Последовательность не сходится, поэтому 1 − 2 + 3 − 4 + … не является суммируемой по Чезаро.
Есть два широко известных обобщения суммирования методом Чезаро: концептуально более простое среди них является последовательностью методов (H, n) для натуральных чисел n, где сумма (H, 1) — это сумма по Чезаро, а высшие методы получаются многократным применением метода суммирования по Чезаро. В примере выше, чётные средние сходятся к 1⁄2, в то время как нечётные равны нулю, поэтому среднее арифметическое средних арифметических сходится к среднему между нулём и 1⁄2, что составляет1⁄4[1]:9 [4]:17-18 Поэтому 1 − 2 + 3 − 4 + … является (H, 2), дающим сумму 1⁄4.
«H» — это сокращение от фамилии Отто Гёльдера, который в 1882 году доказал первым то, что сейчас математики расценивают как связь между суммированием методом Абеля и суммированием(H, n); ряд 1 − 2 + 3 − 4 + … использовался им в качестве первого примера.[3]:118 [5]:10 Тот факт, что 1⁄4 является суммой (H, 2) последовательности 1 − 2 + 3 − 4 + … гарантирует, что это также и абелева сумма; это будет непосредственно доказано ниже.
Другое часто формулируемое обобщение суммирования методом Чезаро — это последовательность методов (C, n). Было доказано, что суммирование (C, n) и (H, n) дают одинаковые результаты, но имеют разную историю. В 1887 году Чезаро близко подошёл к тому, чтобы дать определение суммированию (C, n), но ограничился приведением нескольких примеров. В частности, он получил сумму 1⁄4 для 1 − 2 + 3 − 4 + …, методом, который может быть переформулирован как (C, n), но не воспринимался таковым в своё время. Он формально определил методы (C, n) в 1890 году, для формулирования своей теоремы, гласящей что произведение Коши (C, n)-суммируемого и (C, m)-суммируемого рядов являются (C, m + n + 1)-суммируемыми.[3]:123-128
Суммирование по Абелю
 Некоторые значения 1−2x+3x²+…; 1/(1 + x)²; и пределы при стремлении к единице
Некоторые значения 1−2x+3x²+…; 1/(1 + x)²; и пределы при стремлении к единице
В отчёте 1749 года Эйлер признавал, что ряд расходится, но всё равно планировал найти его сумму:
…когда было сказано, что сумма ряда 1−2+3−4+5−6 и т. д. составляет 1⁄4, это должно было показаться парадоксальным. Складывая 100 членов этого ряда, мы получаем −50, однако сумма 101 члена даёт +51, что очень сильно отличается от 1⁄4 и отличается ещё сильнее с увеличением числа членов. Но я уже раньше замечал, что необходимо дать слову sum более широкое значение….[6]:2
Эйлер предлагал обобщение понятия «сумма ряда» несколько раз. В случае для 1 − 2 + 3 − 4 + …, его идеи похожи на то, что сейчас называется методом суммирования Абеля:
…более нет сомнений, что сумма ряда 1−2+3−4+5 + и т. д. — 1⁄4; поскольку это вытекает из раскрытия формулы 1⁄(1+1)2, значение которой, несомненно, 1⁄4. Идея становится понятнее при рассмотрении обобщённого ряда 1 − 2x + 3x² − 4x³ + 5x4 − 6x5 + &c. возникающего при раскрытии выражения 1⁄(1+x)2, которому этот ряд будет эквивалентен после того как мы присвоим x = 1.[6]:3, 25
Есть много способов увидеть, что как минимум для абсолютных значений |x| < 1, Эйлер прав в том, что
Можно раскрыть правую часть по Тейлору, либо применить формальный процесс деления многочленов столбиком[7]:23. Начиная с левой части, можно использовать общую эвристику, приведённую выше, и перемножить (1+x) на себя[8], или возвести в квадрат ряд 1 − x + x2 − …. Эйлер, по-видимому, также предложил почленно продифференцировать этот ряд[6]:3, 26.
С современной точки зрения, последовательность 1 − 2x + 3x² − 4x³ + … не определяет функцию в точке x = 1, поэтому это значение не может быть просто подставлено в результирующее выражение. Поскольку функция определена для всех |x| < 1, можно вычислять предел при стремлении x к единице, и это будет определением абелевой суммы:
Эйлер и Борель
 Суммирование по Эйлеру 1⁄2 − 1⁄4
Суммирование по Эйлеру 1⁄2 − 1⁄4
Эйлер применил к последовательностям другой подход: преобразование Эйлера, одно из своих изобретений. Чтобы вычислить преобразование Эйлера, начинают с последовательности положительных членов — в данном случае 1, 2, 3, 4, …. Первый член этой последовательности обозначен a0.
Далее нужно получить последовательность конечных разностей среди 1, 2, 3, 4, …; это просто 1, 1, 1, 1, …. Первый элемент этой новой последовательности обозначается Δa0. Преобразование Эйлера также зависит от разности разностей и более высоких итераций, но все разности среди 1, 1, 1, 1, ... равны 0. В таком случае преобразование Эйлера для 1 − 2 + 3 − 4 + … определяется следующим образом:
В современной терминологии, 1 − 2 + 3 − 4 + … называется суммируемым по Эйлеру, с суммой равной 1⁄4.
Суммируемость по Эйлеру также предполагает ещё один вид суммируемости. Представляя 1 − 2 + 3 − 4 + … как
получается сходящийся в каждой точке ряд:
Таким образом, борелева сумма ряда 1 − 2 + 3 − 4 + … составляет[4]:59:
Разделение шкал
Саичев и Войчинский пришли к значению 1 − 2 + 3 − 4 + … = 1⁄4, применяя два физических принципа: отбрасывание бесконечно малых и разделение шкал. Точнее, эти принципы помогли им сформулировать широкое семейство «методов φ-суммирования», все из которых дают сумму 1⁄4:
- Если φ(x) — это функция, первая и вторая производная которой непрерывно интегрируема на (0, ∞), такая что φ(0) = 1 и пределы φ(x) и xφ(x) при стремлении к +∞ оба равны нулю, то[9]:260-264:
Этот результат является обобщением абелева суммирования которое получается заменой φ(x) = exp(−x). Общее утверждение может быть доказано при помощи группирования по парам членов ряда по m и преобразовывая выражение в интеграл Римана. Относительно последнего шага, в соответствующем доказательстве для 1 − 1 + 1 − 1 + … применяется теорема Лагранжа о среднем значении, но здесь требуется более сильная форма Лагранжа теоремы Тейлора.
Обобщения ряда
 Выдержки из стр.233 работы E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum. Эйлер суммирует ряды подобного типа, около 1755.
Выдержки из стр.233 работы E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum. Эйлер суммирует ряды подобного типа, около 1755.
Трёхкратное произведение Коши для ряда 1 − 1 + 1 − 1 + … даёт ряд 1 − 3 + 6 − 10 + …, - знакочередующийся ряд из треугольных чисел, его абелева и эйлерова суммы равны 1⁄8.[10]:313 Четырёхкратное произведение Коши ряда 1 − 1 + 1 − 1 + … даёт ряд 1 − 4 + 10 − 20 + …, - знакочередующийся ряд из тетраэдральных чисел, абелева сумма которого равна 1⁄16.
Другое обобщение ряда 1 − 2 + 3 − 4 + … возможно в несколько другом направлении: это семейство рядов 1 − 2n + 3n − 4n + … для других значений n. При положительных n подобный ряд имеет следующую абелеву сумму:
где Bn — числа Бернулли. Для чётных n, это сводится к
Последняя сумма стала объектом насмешек со стороны Нильса Абеля в 1826:
«Расходящиеся ряды — это всецело работа дьявола, и стыд тому, кто пытается найти какие-либо доказательства относительно них. Можно получить из них, что захочешь, и это они породили так много горя и парадоксов. Можно ли представить что-либо более ужасное, чем сказать, что
0 = 1 − 2n + 3n − 4n + и т. д. где n — положительное число. Здесь есть над чем посмеяться, друзья.» [11]:80Учитель Чезаро, Эжен Каталан, также пренебрежительно относился к расходящимся рядам. Под влиянием Каталана, Чезаро изначально характеризовал «условные формулы» для ряда 1 − 2n + 3n − 4n + ... как «абсурдные выражения», и в 1883 Чезаро выражал общепринятый взгляд, что эти формулы ошибочны, но могут в чём-то быть формально полезны. Наконец, в своей работе Sur la multiplication des séries 1890 года Чезаро пришёл к современному подходу, начиная с определений[3]:120-128.
Ряды были также исследованы для нецелых значений n; они дают эта-функцию Дирихле. Отчасти мотивацией Эйлера к изучению рядов, связанных с рядом 1 − 2 + 3 − 4 + …, стало функциональное уравнение для эта-функции, которое непосредственно ведёт к функциональному уравнению для дзета-функции Римана. Эйлер уже был знаменит нахождением значений этих функций для положительных чётных целых чисел (включая решение базельской проблемы), и попытался найти значения и для положительных нечётных целых чисел (включая постоянную Апери) — эта проблема не разрешена по сей день. Работать методами Эйлера с эта-функцией несколько проще, потому что её ряды Дирихле везде суммируемы по Абелю; ряды Дирихле дзета-функции гораздо сложнее суммировать там, где они расходятся[6]:20-25. К примеру, 1 − 2 + 3 − 4 + … в дзета-функции соответствует знакопостоянный ряд 1 + 2 + 3 + 4 + …, который используется в современной физике, но требует гораздо более сильных методов суммирования.
Примечания
- ↑ 1 2 3 4 Hardy G.H. Divergent Series. — Clarendon Press, 1949. — ISBN LCCN 91-75377
- ↑ Beals Richard Analysis: an introduction. — Cambridge UP, 2004. — ISBN 0-521-60047-2
- ↑ 1 2 3 4 Ferraro, Giovanni (June 1999). «The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics». Archive for History of Exact Sciences 54 (2): 101–135. DOI:10.1007/s004070050036.
- ↑ 1 2 3 Weidlich John E. Summability methods for divergent series. — Stanford M.S. theses, 1950.
- ↑ Tucciarone, John (January 1973). «The development of the theory of summable divergent series from 1880 to 1925». Archive for History of Exact Sciences 10 (1-2): 1–40. DOI:10.1007/BF00343405.
- ↑ 1 2 3 4 Euler, Leonhard; Lucas Willis; and Thomas J Osler Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series. The Euler Archive (2006). Архивировано из первоисточника 10 июля 2012. Проверено 22 марта 2007. ; Работа была написана в 1749 году, но изначально издана только в 1968-м: Euler, Leonhard (1768). «Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques». Memoires de l'academie des sciences de Berlin 17: 83–106.
- ↑ Lavine Shaughan Understanding the Infinite. — Harvard UP, 1994. — ISBN 0-674-92096-1
- ↑ Vretblad Anders Fourier Analysis and Its Applications. — Springer, 2003. — ISBN 0-387-00836-5
- ↑ Saichev, A.I., and W.A. Woyczyński Distributions in the physical and engineering sciences, Volume 1. — Birkhaüser, 1996. — ISBN 0-8176-3924-1
- ↑ Kline, Morris (November 1983). «Euler and Infinite Series». Mathematics Magazine 56 (5): 307–314. DOI:10.2307/2690371.
- ↑ Grattan-Guinness Ivor The development of the foundations of mathematical analysis from Euler to Riemann. — MIT Press, 1970. — ISBN 0-262-07034-0
- Ряды
- Математические парадоксы
Wikimedia Foundation. 2010.
dic.academic.ru
Соотношение
У этого термина существуют и другие значения, см. Отношение.Соотношение в математике (отношение, пропорция) — это взаимосвязь между двумя числами одного рода[1] (предметами, действиями, явлениями, свойствами (признаками), понятиями, объектами, например, людьми (студентами), чайными ложками, единицами чего-либо одинаковой размерности), обычно выражаемое как «a к b» или a: b, а иногда выражаемое арифметически как безразмерное отношение (результат деления) двух чисел[2], непосредственно отображающее, сколько раз первое число содержит второе (не обязательно целое).[3]
Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого. Например, предположим, что у кого-то есть 8 апельсинов и 6 лимонов в вазе для фруктов, соотношение апельсинов и лимонов составит 4:3 (что эквивалентно 8:6), а соотношение лимонов и апельсинов составит 3:4. Кроме того, количество апельсинов относительно общего количества фруктов составит 4:7 (что эквивалентно 8:14). Соотношение 4:7 можно преобразовать в дробь 4/7, показывающую, какую долю от общего числа фруктов составляют апельсины.
Обозначения и термины
Соотношение чисел A и B можно представить как:[2]
- отношение A к B
- A:B
- долю A (рациональное число), которая представляет собой результат деления A на B
- A B {\displaystyle {\tfrac {A}{B}}}
Числа A и B в данном контексте иногда называют членами (terms), где A — антецедент, а B — консеквент.
Пропорция, выражающая равенство соотношений A:B и C:D, записывается как A:B=C:D или A:B::C:D. Читается:
A относится к B как C относится к D.И в данном случае, A, B, C, D называются членами пропорции. A и D — крайние члены пропорции, а B и C — средние члены. Равенство трёх и более соотношений называется непрерывной пропорцией (continued proportion, ряд отношений).[2]
Иногда в соотношениях три и более членов. Например, размеры предмета с сечением два к четырём и длиной десять сантиметров составят 2:4:10.
История и этимология
 В Викисловаре есть статья «соотношение»
В Викисловаре есть статья «соотношение»
Невозможно проследить истоки концепции соотношения, поскольку идеи, из которых она развилась, должны были быть известны дописьменным культурам. Например, идея того, что одна деревня вдвое больше другой, настолько базовая, что была бы понятна даже в доисторическом обществе.[4]
Для обозначения отношения греки использовали термин др.-греч. λόγος, которое латиняне передавали как ratio («разумное основание»; как в слове «рациональный») или как proportio. (Рациональное число можно представить как результат отношения двух целых чисел.) Более современная интерпретация евклидова значения ближе к «вычисление» или «расчёт».[3] Боэций («Основы арифметики», «Основы музыки», начало VI в.) использовал слово proportio (наряду с ratio, comparatio и habitudo) для обозначения отношения и proportionalitas (перевод др.-греч. ἀναλογία) для обозначения пропорции (отношения отношений)[5]. Такое терминоупотребление (в связи с широчайшей распространённостью «Арифметики» и «Музыки» Боэция) практиковалось и в Средние века.
Евклид объединил в «Началах» результаты из более ранних источников. Пифагорейцы развили теорию соотношения и пропорции в приложении к числам[6]. Пифагорейская концепция числа включая лишь то, что сейчас называют рациональными числами, что навело сомнения на применимость теории в геометрии, где, как также обнаружили пифагорейцы, существуют несоизмеримые размеры, соответствующие иррациональным числам. Открытие теории отношений, не предполагавшей соизмеримость, вероятно, принадлежит Евдоксу Книдскому. В Книге VII «Начал» приведена и более ранняя теория отношений соизмеримых величин[7].
Существование нескольких теорий выглядит ненужным усложнением для современного взгляда, поскольку соотношения, во многом, определяются результатом деления. Однако, это довольно недавнее открытие, что можно увидеть на примере того, что современные учебники по геометрии до сих пор используют различную терминологию для соотношений (ratio) и результатов деления (quotient, частное). Причин для этого две. Во-первых, существовало вышеупомянутое нежелание признавать иррациональные числа как истинные числа. Во-вторых, нехватка широко используемых символов (обозначений) для замены уже устоявшейся терминологии соотношений задержало полное принятие дробей как альтернативы вплоть до XVI века.[8]
Определения Евклида
В книге V «Начал» Евклида 18 определений, касающихся соотношений[9]. Кроме того, Евклид использует идеи, которые были в настолько широком употреблении, что он не даёт им определений. Первые два определения гласят, что часть количества есть другое количество, которое «измеряет» его, и наоборот, кратное для количества есть другое количество, измеряемое им. В современных терминах, это означает, что кратное для количества есть это количество, умноженное на целое число, большее единицы, а часть количества (то есть делитель) при умножении на число, большее единицы, даёт то количество.
Эвклид не даёт определения слова «измерять». Тем не менее, можно предположить, что, если количество принимается за единицу измерения, а другое количество представлено как общее количество таких единиц измерения, то первое количество измеряет второе. Заметим, эти определения повторяются почти слово в слово как определения 3 и 5 в книге VII.
Определение 3 разъясняет, что такое соотношение в общем смысле. Оно не является математически строгим и некоторые исследователи приписывают его редакторам, а не самому Евклиду.[10] Евклид определяет соотношение между двумя количествами одного вида, например двух отрезков или двух площадей, но не соотношение длины к площади. Определение 4 указывает это ещё более строго. Оно утверждает, что соотношение между двумя количествами существует, если есть кратное для каждого, превышающее другое. В современных терминах: соотношение между количествами p и q существует, если существуют целые числа m и n такие, что mp>q и nq>m. Это условие известно как аксиома Архимеда.
Определение 5 наиболее сложное и трудное для понимания. Оно объясняет, что означает равенство для двух соотношений. Сегодня можно просто заявить, что соотношения равны, если равны результаты деления членов, но Евклид не признавал существование результатов деления для несоизмеримых величин, поэтому для него такое определение было бы бессмысленным. Поэтому требовалось более тонкое определение для случая количеств, не измеряющих друг друга напрямую. Хотя может быть невозможно присвоить соотношению рациональное значение, но вполне возможно сравнить соотношение с рациональным числом. А именно, для двух количеств p и q, а также рационального числа m/n, мы можем сказать, что соотношение p к q меньше, равно или больше m/n, когда np меньше, равно или больше mq, соответственно. Евклидово определение равенства можно сформулировать так: два соотношения равны, когда они одинаково себя ведут, будучи одновременно меньше, равны или больше любого рационального числа. В современной нотации это выглядит так: для данных количеств p, q, r и s выполняется p:q::r:s, если для любых положительных целых чисел m и n выполняется отношение npmq, np=mq, np>mq в соответствии с nrms, nr=ms, nr>ms. Есть примечательное сходство между этим определением и теорией Дедекиндова сечения, используемого в современной теории иррациональных чисел[11].
Определение 6 гласит, что количества с одинаковым соотношением пропорциональны или состоят в пропорции. Евклид использует греческое слово ἀναλόγον (analogon), с тем же корнем, что и λόγος, от которого произошло слово «аналог».
Определение 7 объясняет, что значит для соотношения быть меньше или больше другого, и основывается на идеях из определения 5. В современной нотации: для данных количеств p, q, r и s выполняется p:q>r:s, если существуют положительные целые числа m и n такие, что np>mq и nr≤ms.
Как и в случае с определением 3, определение 8 некоторыми исследователями рассматривается как позднее включение редакторов. Оно гласит, что три члена p, q и r находятся в пропорции, если p:q::q:r. Это расширяется на 4 члена p, q, r и s как p:q::q:r::r:s и т. д. Последовательности, обладающие таким свойством, что соотношения последовательных членов равны, называются геометрическими прогрессиями. Определения 9 и 10 применяют это, говоря, что, если p, q и r состоят в пропорции, то p:r есть двойное отношение (duplicate ratio, отношение квадратов) для p:q, а если p, q, r и s находятся в пропорции, то p:s есть тройное отношение (triplicate ratio, отношение кубов) для p:q. Если p, q и r находятся в пропорции, то q называется средним пропорциональным (или геометрическим средним) для p и r. Подобным образом, если p, q, r и s находятся в пропорции, то q и r называют средними пропорциональными для p и s.
Процентное соотношение
Если умножить все количества в соотношении на одно и то же число, то соотношение не изменится. Например, соотношение 3:2 есть то же самое, что 12:8. Обычно члены пропорции уменьшают до наименьшего общего знаменателя либо выражают их в долях ста (процент). Иногда для удобства сравнения соотношения представляют в виде n:1 или 1:n.
Если смесь содержит вещества A, B, C и D в соотношении 5:9:4:2, то в ней 5 частей A приходится на каждые 9 частей B, 4 части C и 2 части D. Поскольку 5+9+4+2=20, то всего смесь содержит 5/20 A (5 частей из 20), 9/20 B, 4/20 C и 2/20 D. Если эти числа, деленные на общую сумму, умножить на 100, то получаем проценты: 25 % A, 45 % B, 20 % C и 10 % D (эквивалентно написанию соотношения в виде 25:45:20:10).
Пропорции
Если два или более количества, состоящих в пропорциональном соотношении, являются всеми количествами, задействованными в конкретной ситуации, например, два яблока и три апельсина в корзине, в которой нет других фруктов, то можно сказать, что «целое» содержит пять частей, состоящих из двух частей яблок и трёх частей апельсинов. В данном случае, 2 5 {\displaystyle {\tfrac {2}{5}}} , или 40 % целого, — это яблоки, а 3 5 {\displaystyle {\tfrac {3}{5}}} , или 60 % целого, — это апельсины. Такое сравнение определённого количества с «целым» иногда называют пропорцией. Пропорции иногда выражают в процентах, как указано выше.
Другие применения
- Соотношения часто используются для простых растворов в химии и биологии (степень разбавления).
- Шансы выигрыша в играх выражают в виде соотношения.
- Возможны соотношения количеств, измеряемых в разных единицах измерения.
ru.wikipedia.org
Хэлп ми плиз!
1. Случайная величина принимает все нечетные значения от -3 до 5 с равными вероятностями. Найдите ее математическое ожидание.
2. В таблице дано распределение случайной величины X. Чему равно E(X)?
Значение 1 2 3 4 5 6 7 8
Вероятность 0,16 0,19 0,02 0,06 0,11 0,06 0,15 0,25
3. Игральную кость бросили 64 раза. Найдите математическое ожидание, дисперсию и стандартное отклонение случайной величины X, равной числу выпадения четного числа очков.
4*. Серию испытаний Бернулли проводят дважды. В первый раз вероятность успеха была равна , а во второй раз вероятность успеха равнялась . В обоих случаях случайная величина S — число наступивших успехов. В каком из случаев ожидаемый разброс величины S больше?
Jurasea / vikkiv
1)
-3 , -1 , +1 , +3, +5 ←Xi
0.2,0.2,0.2,0.2,0.2 ←Pi
E(X) = M = ∑Pi•Xi = 0.2•(-3-1+1+3+5) = 0.2•5 = 1
2)
E(X) = M = ∑Pi•Xi = (0.16•1)+(0.19•2)+...+(0.25•8)
E(X) = M = 0.16+0.38+0.06+...+0.36+1.05+2 = 4.8
3) По Бернулли:
Четное значение в одном опыте : p=1/2
Противоположное событие : q=1-p=1-1/2=1/2
n=64
M=n•p=64•1/2=32 [математическое ожидание]
D=σ²=n•p•q=64•1/2•1/2=16 [дисперсия]
σ=√D=√16=4 [стандартное отклонение]
4)
Так ведь данные на самом-то деле отсувствуют, для решения нет вероятностей успехов первого и второго раза.
Что означает равенство 2 -1= √3?
Почему бы вам не использовать в своих примерах знак ≡ вместо = ? По крайне мере ваши записи не выглядели бы настолько несуразно. — 3 года назадМихаил белодедов
Если в прямоугольном треугольнике гипотенуза равна двум, а один из катетов имеет единичную длину, то оставшийся катет неизбежно должени иметь длину корень квадратный из трёх. Другого разумного объяснения я не вижу.
Spin
Если это равенство получилось в результате расчетов, то думаю, что такое равенство означает, что в расчетах была допущена ошибка.
Левая сторона равенства равна 1 (2-1=1), правая корень из трех. Ясно, что левая и правая стороны равенства не равны, значит и равенство не выполняется.
Или ошибка в том, что вместо знака "равно" надо было ставить знак "не равно".
bolshoyvopros.ru
Категория годности к военной службе . Что означают графы 1 2 3 и тд ?
Просто дед
Категории годности обозначаются буквами, а не цифрами. А цифры добавляются к буквам для большей информативности.
-----------------------------------------------------------------
17. Врачи-специалисты по результатам медицинского освидетельствования граждан при первоначальной постановке на воинский учет и призыве на военную службу дают заключение о годности к военной службе по следующим категориям:
А - годен к военной службе;
Б - годен к военной службе с незначительными ограничениями;
В - ограниченно годен к военной службе;
Г - временно не годен к военной службе;
Д - не годен к военной службе.
---------------------------------------------------------------------
А и Б призываются, остальные нет. Д это совсем исключаются с воинского учета. С категорией В зачисляют в запас. Ну а Г это просто отсрочка по состоянию здоровья максимум на 1 год.
 Шалом что значит
Шалом что значит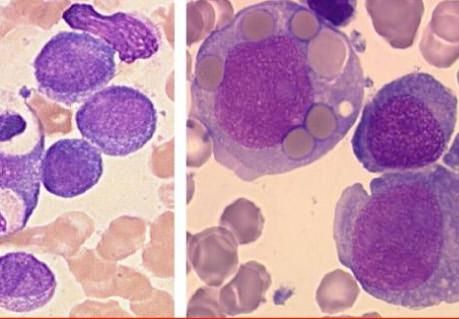 Цитограмма без особенностей что это значит
Цитограмма без особенностей что это значит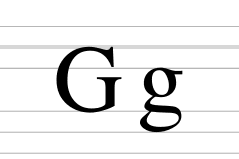 Что значит g
Что значит g Что значит ip
Что значит ip Что значит lte в телефоне
Что значит lte в телефоне Что значит nfc в телефоне
Что значит nfc в телефоне Чистота бриллианта 5 5 что значит
Чистота бриллианта 5 5 что значит 666 Что значит
666 Что значит Что значат кольца на пальцах
Что значат кольца на пальцах Что значит авторизация
Что значит авторизация Снятся пауки что это значит
Снятся пауки что это значит 21 21 Что значит время на часах
21 21 Что значит время на часах