Формула интерполяции между двумя значениями

Интерполяция

Обратная интерполяция

/ Material_studentam_po_RGR_BZhD / Как выполнить интерполяцию

1.4. Интерполяционная формула Лагранжа

Подскажите как использовать формулу интерполяции и какую в решении задач по термодинамике (теплотехнике)

Интерполяция (координат)

Определения

Пример

В языках программирования

Способы интерполяции

Смежные концепции

Применение интерполяции для составления таблиц

Предметный указатель

1.4.1.Организация ручных вычислений по формуле Лагранжа

1.4.2. Реализация алгоритма интерполяции по формулам Лагранжа в среде программы Microsoft Excel

Fortran

C++

Интерполяция методом ближайшего соседа

Интерполяция многочленами

Обратное интерполирование (вычисление x при заданной y)

Интерполяция функции нескольких переменных

Другие способы интерполяции

У этого термина существуют и другие значения, см. Интерполяция. О функции, см.: Интерполянт.

Интерполя́ция, интерполи́рование (от лат. inter–polis — «разглаженный, подновлённый, обновлённый; преобразованный») — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Термин «интерполяция» впервые употребил Джон Валлис в своём трактате «Арифметика бесконечных» (1656).

В функциональном анализе интерполяция линейных операторов представляет собой раздел, рассматривающий банаховы пространства как элементы некоторой категории.

Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.

Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса — Торина (Riesz-Thorin theorem) и теорема Марцинкевича (Marcinkiewicz theorem), являющиеся основой для множества других работ.

Рассмотрим систему несовпадающих точек x i {\displaystyle x_{i}} ( i ∈ 0 , 1 , … , N {\displaystyle i\in {0,1,\dots ,N}} ) из некоторой области D {\displaystyle D} . Пусть значения функции f {\displaystyle f} известны только в этих точках:

y i = f ( x i ) , i = 1 , … , N . {\displaystyle y_{i}=f(x_{i}),\quad i=1,\ldots ,N.}

Задача интерполяции состоит в поиске такой функции F {\displaystyle F} из заданного класса функций, что

F ( x i ) = y i , i = 1 , … , N . {\displaystyle F(x_{i})=y_{i},\quad i=1,\ldots ,N.}

Точки x i {\displaystyle x_{i}} называют узлами интерполяции, а их совокупность — интерполяционной сеткой.
Пары ( x i , y i ) {\displaystyle (x_{i},y_{i})} называют точками данных или базовыми точками.
Разность между «соседними» значениями Δ x i = x i − x i − 1 {\displaystyle \Delta x_{i}=x_{i}-x_{i-1}} — шагом интерполяционной сетки. Он может быть как переменным, так и постоянным.
Функцию F ( x ) {\displaystyle F(x)} — интерполирующей функцией или интерполянтом.

1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений x {\displaystyle x} определяет соответствующие значения f {\displaystyle f} :

x {\displaystyle x} f ( x ) {\displaystyle f(x)}


0
1	0,8415
2	0,9093
3	0,1411
4	−0,7568
5	−0,9589
6	−0,2794

Интерполяция помогает нам узнать, какое значение может иметь такая функция в точке, отличной от указанных точек (например, при x = 2,5).

К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.

2. Найти промежуточное значение (способом линейной интерполяции).

6000	15.5
6378	?
8000	19.2

? = 15.5 + ( 6378 − 6000 ) 8000 − 6000 ∗ ( 19.2 − 15.5 ) 1 = 16.1993 {\displaystyle ?=15.5+{\frac {(6378-6000)}{8000-6000}}*{\frac {(19.2-15.5)}{1}}=16.1993}

Пример линейной интерполяции для функции y = 3 x + x 2 {\displaystyle y=3x+x^{2}} . Пользователь может ввести число от 1 до 10.

program interpol integer i real x, y, xv, yv, yv2 dimension x(10) dimension y(10) call prisv(x, i) call func(x, y, i) write(*,*) 'enter number : ' read(*,*) xv if ((xv >= 1).and.(xv xv)) then yv2 = ((xv - x(i)) * (y(i+1) - y(i)) / (x(i+1) - x(i))) + y(i) end if end do end subroutine

int main() { system("COLOR 0A"); double ob, x1, x2, y1, y2, p1, p2, pi, skolko, status; system("echo Интерполяция X1 - X2 "); system("echo Ввести число: "); cin >> ob; system("echo Например 62, C1 = 60, L1 = 1.31, C2 = 80, L2 = 1.29"); cout > x1; cout > x2; cout > y1; cout > y2; p1 = y1 - x1; p2 = y2 - x2; pi = p2 / p1; skolko = ob - x1; status = x2 + (pi * skolko); cout

Простейшим способом интерполяции является интерполяция методом ближайшего соседа.

На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).

Линейная интерполяция
Интерполяционная формула Ньютона
Метод конечных разностей
ИМН-1 и ИМН-2
Многочлен Лагранжа (интерполяционный многочлен)
Схема Эйткена
Сплайн-функция
Кубический сплайн

Полином Лагранжа
Обратное интерполирование по формуле Ньютона
Обратное интерполирование по формуле Гаусса

Билинейная интерполяция
Бикубическая интерполяция

Рациональная интерполяция
Тригонометрическая интерполяция

Экстраполяция — методы нахождения точек за пределами заданного интервала (продление кривой)
Аппроксимация — методы построения приближённых кривых

ru.wikipedia.org

на классе функций из пространства C2 [a, b], графики которых проходят через точки массива (xi, yi), i = 0, 1, . . . , m.

Решение. Среди всех функций, которые проходят через опорные точки (xi, f(xi)) и принадлежат упомянутому пространству, именно кубический сплайн S(x), удовлетворяющий краевым условиям S00(a) = S00(b) = 0, предоставляет экстремум (минимум) функционала I(f).

Часто на практике возникает задача о поиске по заданному значению функции значения аргумента. Эта задача решается методами обратной интерполяции. Если заданная функция монотонна, то обратную интерполяцию проще всего осуществить путем замены функции аргументом и наоборот и последующего интерполирования. Если заданная функция не монотонна, то этим приемом воспользоваться нельзя. Тогда, не меняя ролями функцию и аргумент, записываем ту или иную интерполяционную формулу; используя известные значения аргумента и, считая функцию известной, решаем полученное уравнение относительно аргумента.

Оценка остаточного члена при использовании первого приема будет такая же, как и при прямой интерполяции, только производные от прямой функции нужно заменить производными от обратной функции. Оценим ошибку второго метода. Если нам задана функция f(x) и Ln (x) — интерполяционный многочлен Лагранжа, построенный для этой функции по узлам x0, x1, x2, . . . , xn, то

f(n+1)(ξ)

f (x) − Ln (x) =(n + 1)! (x− x0) . . . (x− xn) .

Предположим, что нам надо найти значение x¯, при котором f (¯x) = y¯ (y¯ задано). Будем решать уравнение Ln (x) = y¯ . Получим некоторое значение x¯. Подставляя в предыдущее уравнение, получим:

•Назад•Первая•Предыдущая•Следующая•Последняя•Перейти•Предметный указатель

Mn+1

	f(n+1)(ξ)
f (x¯) − Ln (x¯) = f (x¯) − y¯ = f (x¯) − f (¯x) =				$n (x¯) .
f (x¯) − Ln (x¯) = f (x¯) − y¯ = f (x¯) − f (¯x) =			(n + 1)!	$n (x¯) .
Применяя формулу Лангранжа, получим
(x¯ − x¯) f0 (η) =	f(n+1)(ξ)
		$n (x¯) ,
	(n + 1)	$n (x¯) ,
где η находится между x¯ и x¯. Если [a, b] — интервал, который содержит x¯ и x¯ и min							f0 (x)		= m	= 0, то
		x		[a,b]	\|	\|	1	6

из последнего выражения вытекает:

|x¯ − x¯| 6m1 (n + 1)! |$n (x¯)| .

При этом, конечно, предполагается, что уравнение Ln (x) = y¯ мы решили точно.

Теория интерполяции имеет применение при составлении таблиц функций. Получив такую задачу, математик должен решить перед началом вычислений ряд вопросов. Должна быть избрана формула, по которой будут проводиться вычисления. Эта формула может изменяться от участка к участку. Обычно формулы для вычисления значений функции бывают громоздкими и потому их используют для получения некоторых опорных значений и потом, путем субтабулирования, сгущают таблицу. Формула, которая дает опорные значения функции, должна обеспечивать нужную точность таблиц с учетом следующего субтабулирования . Если нужно составить таблицы с постоянным шагом, то сначала надо определить ее шаг.

•Назад•Первая•Предыдущая•Следующая•Последняя•Перейти•Предметный указатель

Чаще всего таблицы функций составляются так, чтобы была возможной линейная интерполяция (то есть интерполяция с использованием первых двух членов формулы Тейлора). В этом случае остаточный член будет иметь вид

R1 (x) =f00 (ξ)h2t(t − 1).

Здесь ξ принадлежит интервалу между двумя соседними табличными значениями аргумента, в котором находится x, а t заключен между 0 и 1. Произведение t(t − 1) принимает наибольшее по модулю

значение при t = 12.Это значение равняется14. Итак,

\|R1 (x)\| 6	M2h2
	8 , где M2 = max \|f00 (ξ)\| .

Чтобы ошибка интерполяции не превышала по абсолютной величине a, необходимо выбрать h , ко-

торое удовлетворяло бы условию h 6	8a	.

	M2

Нужно помнить, что рядом с этой ошибкой — ошибкой метода, при практическом вычислении промежуточных значений будут возникать еще неустранимая погрешность и погрешность округлений. Как мы видели раньше, неустранимая погрешность при линейной интерполяции будет равной погрешности табулированных значений функции. Погрешность округления будет зависеть от вычислительных средств и от программы вычислений.

•Назад•Первая•Предыдущая•Следующая•Последняя•Перейти•Предметный указатель

разделенные разности второго порядка, 8 первого порядка,8

сплайн, 15

узлы интерполяции, 4

•Назад•Первая•Предыдущая•Следующая•Последняя•Перейти•Предметный указатель

StudFiles.ru

Формула для интерполяции табличных данных

Используется во 2-ом действии, когда количество НХР (Q, т) из условия имеет промежуточное значение между 100 т и 300 т.

(Исключение: если Q по условию равно 100 или 300 – то интерполяция не нужна).

где

y_o - Ваше исходное количество НХР из условия, в тоннах

(соответствует букве Q)

y₁ – меньшее ближайшее к Вашему значение количества НХР, в тоннах

(из табл.11-16, как правило равно 100).

y₂ – большее ближайшее к Вашему значение количества НХР, в тоннах

(из табл.11-16, как правило равно 300).

x₁ – табличное значение глубины распространения облака зараженного воздуха (Г_т), соответственно y₁(x₁расположено напротив y₁), км.

x₂ – табличное значение глубины распространения облака зараженного воздуха (Г_т), соответственно y₂(x₂расположено напротив y₂), км.

x₀– искомое значение Г_т соответствующее y_o(по формуле).

Пример.

Условие:

НХР – хлор; Q = 120 т;

Вид СВСП (степень вертикальной стойкости воздуха) – инверсия.

Найти Г_т - табличное значение глубины распространения облака зараженного воздуха.

Решение:

Просматриваем таблицы 11-16 и находим данные соответствующие вашему условию (хлор, инверсия).

Подходит таблица 11.

Выбираем значения y₁, y_2, x₁, x₂. Важно – скорость ветра берем 1 м/с., температуру берем – 20 оС.
Подставляем выбранные значения в формулу и находим x₀.

Важно – расчет правильный, если x₀будет иметь значение где-то междуx₁, x₂.

Ответ: Г_т = х₀ = 90,38 км.

StudFiles.ru

Предложенный Лагранжем алгоритм построения интерполирующих

функций по таблицам (1) предусматривает построение интерполяционного многочлена Ln(x) в виде

Ln (x)= l0 (x)+ l1 (x)+...+ ln (x)		(11)
где li(x) - многочлен степениn, для которого выполняются условия
Y	, если i = k,	(12)
li(xk) = i	если i ≠ k.
0,

Очевидно, что выполнение для (10) условий (11) определяет выполнение условий (2) постановки задачи интерполяции.

Многочлены li(x) записываются следующим образом

Отметим, что ни один множитель в знаменателе формулы (14) не равен нулю. Вычислив значения констант сi, можно использовать их для вычисления значений интерполируемой функции в заданных точках.

Формула интерполяционного многочлена Лагранжа (11) с учётом формул (13) и (14) может быть записана в виде

Ln (x)= ∑n

qi (x − x0 )(x − x1 )•K• (x − xi −1 )(x − xi +1 )•K• (x − xn )

(15)

i=0

Непосредственное применение формулы Лагранжа приводит к большому числу однотипных вычислений. Для таблиц небольшой размерности эти вычисления могут быть выполнены как вручную, так и в среде программ

Microsoft Excel или OpenOffice.org Calc.

На первом этапе рассмотрим алгоритм вычислений, выполняемых вручную. В дальнейшем эти же вычисления следует повторить в среде

Microsoft Excel или OpenOffice.org Calc.

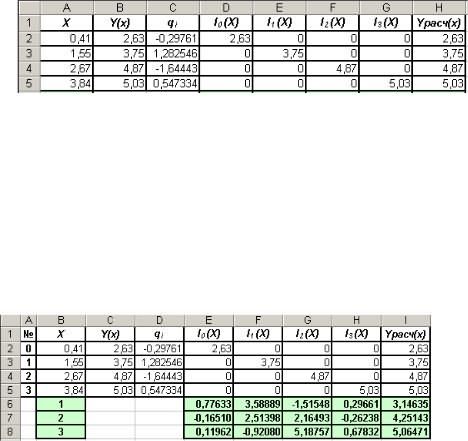
На рис. 6 приведён пример исходной таблицы интерполируемой функции, определяемой четырьмя узлами.

Рис.6. Таблица, содержащая исходные данные для четырёх узлов интерполируемой функции

В третий столбец таблицы запишем вычисляемые по формулам (14) значения коэффициентов qi. Ниже приведена запись этих формул для n=3.

q0=Y0/(x0-x1)/(x0-x2)/(x0-x3)q1=Y1/(x1-x0)/(x1-x2)/(x1-x3)(16) q2=Y2/(x2-x0)/(x2-x1)/(x2-x3)q3=Y3/(x3-x0)/(x3-x1)/(x3-x2)

Следующим шагом в реализации ручных вычисления являются вычисления значений li(x) (j=0,1,2,3), выполняемые по формулам (13).

Запишем эти формулы для рассматриваемого нами варианта таблицы с четырьмя узлами:

l0(x)=q0(x-x1)·(x-x2)·(x-x3),

l1(x)=q1(x-x0)·(x-x2)·(x-x3),

l2(x)=q2(x-x0)·(x-x1)·(x-x3),(17) l3(x)=q3(x-x0)·(x-x1)·(x-x2).

Вычислим значения многочленов li(xj) (j=0,1,2,3) и запишем их в ячейки таблицы. Значения функцииYрасч(x), согласно формуле (11) будут получены в результате суммирования значенийli(xj) по строкам.

Формат таблицы, включающей столбцы вычисленных значений li(xj) и столбец значенийYрасч(x), показан на рис.8.

Рис. 8. Таблица с результатами ручных вычислений, выполненных по формулам (16), (17) и (11) для всех значений аргумента xi

Выполнив формирование таблицы, приведённой на рис. 8, по формулам (17) и (11) можно вычислить значение интерполируемой функции для любого значения аргумента Х. Например, дляХ=1 вычисляем значенияli(1) (i=0,1,2,3):

l0(1)= 0,7763; l1(1)= 3,5889; l2(1)=-1,5155;l3(1)= 0,2966.

Суммируя значения li(1) получим значениеYинтерп(1)=3,1463.

Реализация алгоритма интерполяции начинается, как и при ручных вычислениях с записи формул для вычисления коэффициентов qi На рис. 9 приведена столбцы таблицы с заданными значениями аргумента, интерполируемой функции и коэффициентовqi. Справа от этой таблицы приведены формулы, записываемые в ячейки столбцаС для вычисления значений коэффициентовqi.

вС2: "=B2/((A2-A3)*(A2-A4)*(A2-A5))"Æ q0

вС3: "=B3/((A3-A4)*(A3-A5)*(A3-A2))"Æ q1

вС4: "=B4/((A4-A5)*(A4-A2)*(A4-A3))"Æ q2

вС5: "=B5/((A5-A2)*(A5-A3)*(A5-A4))"Æ q3

Рис. 9 Таблица коэффициентов qi и вычислительные формулы

После ввода формулы q0 в ячейку С2 она протягивается по ячейкам от С3 до С5. После чего формулы в этих ячейках корректируются в соответствии с (16) к виду, приведённому на рис. 9.

Yрасч(xi),

Реализуя формулы (17), запишем формулы для вычисления значений li(x) (i=0,1,2,3) в ячейки столбцов D, E, F и G. В ячейкуD2 для вычисления значенияl0(x0) запишем формулу:

=$C$2*($A2-$A$3)*($A2-$A$4)*($A2-$A$5),

здесь $C$2 - абсолютная ссылка на ячейку со значениемq0, $A2 - ссылка на ячейку, в которую записано значениеx0. Протянув эту формулу по столбцу,

получим значения l0 (xi) (i=0,1,2,3).

Формат ссылки $A2 позволяет протянуть формулу по столбцамE, F, G для формирования вычислительных формул для вычисленияli(x0) (i=1,2,3). При протягивании формулы по строке индекс столбца аргументах не меняется. Для вычисленияli(x0) (i=1,2,3) после протягивания формулыl0(x0) необходимо выполнить их корректировку по формулам (17).

Встолбце Н поместим формулы Excel для суммированияli(x) по формуле

(11)алгоритма.

На рис. 10 показана таблица, реализованная в среде программы Microsoft Excel. Признаком правильности записанных в ячейки таблицы формул и выполненных вычислительных операций являются полученная диагональная матрица li(xj) (i=0,1,2,3),(j=0,1,2,3),повторяющая результаты, приведённые на рис. 8, и столбец значений совпадающих со значениями интерполируемой функции в узлах исходной таблицы.

Рис. 10. Таблица значений li(xj) (j=0,1,2,3) иYрасч(xj)

Для вычисления значений в некоторых промежуточных точках достаточно

вячейки столбца А, начиная с ячейкиА6, ввести значения аргументаХ, для которых требуется определить значения интерполируемой функции. Выделить

впоследней (5-й)строке таблицы ячейки отl0(xn) доYрасч(xn) и протянуть формулы, записанные в выделенных ячейках до строки, содержащей последнее

заданное значение аргумента х.

На рис. 11 приведена таблица, в которой выполнены вычисления значения функции в трёх точках: х=1, х=2 и х=3. В таблицу введён дополнительный столбец с номерами строк таблицы исходных данных.

Рис. 11. Вычисление значений интерполируемых функции по формулам Лагранжа

Для большей наглядности отображения результатов интерполяции построим таблицу, включающую столбец упорядоченных по возрастанию значений аргумента Х, столбец исходных значений функцииY(X) и столбец

StudFiles.ru

Иван шестакович

Самое простое, но и часто не достаточно точная интерполяция - это линейная. Когда у тебя есть уже две известные точки (Х1 У1) и (X2 Y2) а надо найти значения У дня некоторого Х который находится между Х1 и Х2. Тогда формула проста.
У=(У2-У1)*(Х-Х1)/(Х2-Х1)+У1
Кстати эта формула работает и при значениях Х вне пределов промежутка Х1..Х2, но это уже называется экстрополяцией и при значительном расстоянии от этого промежутка дает очень большую погрешность.
Есть много других мат. методов интерполяции - советую почитать учебник или порыться и инете.
Не исключен так же метод графической интерполяции - в ручную нариовать график через известные точки и для требуемго Х находить из графика У. ;)

Роман

У тебя есть два значения. И примерно зависимость (линейтная, квадратичная, ..)
График этой функции проходит через твои две точки. Тебе нужно значение где-то между. Ну и выражаешь!
Например. В таблеце при температуре 22 градуса давление насыщеных паров 120000 Па, а при 26 124000 Па. Тогда при температуре 23 градуса 121000 Па.

li(x)=qi(x-x0)(x-x1)·…·(x-xi-1)(x-xi+1)…(x-xn).

Здесь qj - константа, значение которой определяется с учётом (12) как

, (i = 0,1,2,...,n)

− x0 )...(xi − xi−1 )(xi − xi+1 )...(xi − xn )

Есть сетка координат на карте (изображении).
На ней есть некоторые известные опорные точки (n>3), имеющие по два значения x,y - координаты в пикселах, и координаты в метрах.
Необходимо найти промежуточные значения координат в метрах, зная координаты в пикселах.
Линейная интерполяция не подходит - слишком большая погрешность за пределами линии.
Вот так: (Xc - коорд. в метрах по ох, Xp - коорд. в пикселах по ох, Xc3 - искомое значение по ох)
Xc3= (Xc1-Xc2)/(Xp1-Xp2)*(Xp3-Xp2)+Xc2
Yc3= (Yc1-Yc2)/(Yp1-Yp2)*(Yp3-Yp2)+Yc2

Как найти такую же формулу для нахождения Xc и Yc, учитывая не две (как тут), а N известных опорных точек?

Joka fern lowd

Судя по выписанным формулам, оси систем координат в пикселах и в метрах совпадают?
То есть независимо интерполируется Xp -> Xc и независимо Yp -> Yc. Если нет, то надо использовать двумерную интерполяцию Xp,Yp->Xc и Xp,Yp->Yc, что несколько усложняет задачу.
Далее подразумевается, что координаты Xp и Xc связаны некоторой зависимостью.
Если характер зависимости известен (или предполагается, например, предполагаем, что Xc=a*Xp^2+b*Xp+c), то можно получить параметры этой зависимости (для приведенной зависимости a, b, c) с помощью регрессионного анализа (Метод наименьших квадратов) . В этом методе, если задаться определенной зависимостью Xc(Xp) можно получить формулу для параметров зависимости от опорных данных. Этот метод позволяет, в частности, найти и линейную зависимость, наилучшим образом удовлетворяющую данному набору данных.
Недостаток: В этом методе координаты Xc, полученные по данным опорных точек Xp, могут отличаться от заданных. Как например, аппроксимационная прямая проведенная по экспериментальным точкам, не проходит точно через сами эти точки.
Если же требуется точное соответствие и характер зависимости неизвестен, нужно использовать интерполяционные методы. Простейшим математически является интерполяционный полином Лагранжа, точно проходящий через опорные точки. Однако в силу высокой степени этого полинома при большом числе опорных точек и плохого качества интерполяции, лучше его не использовать. Преимуществом является сравнительно простая формула.
Лучше использовать интерполяцию сплайнами. Суть этого метода в том, что на каждом участке между двумя соседними точками, исследуемая зависимость интерполируется полиномом, а в точках сшивки двух интервалов записываются условия гладкости. Преимуществом этого метода является качество интерполяция. Недостатками -- практически невозможно вывести общую формулу, приходится находить коэффициенты полинома на каждом участке алгоритмически. Другим недостатком является сложность обобщения на двумерную интерполяцию.