Механический смысл производной определение

7.Производная. Геометрический и механический смысл производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Производная.Рассмотрим некоторую функцию y = f ( x ) в двух точках x₀ и x₀ + : f ( x₀ ) и f ( x₀ + ). Здесь через обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f ( x₀ + )  f ( x₀ ) называется приращением функции.Производной функции y = f ( x ) в точке x₀ называется предел:

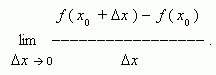
Если этот предел существует, то функция f ( x ) называется дифференцируемой в точке x₀. Производная функции f ( x ) обозначается так:

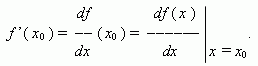
Геометрический смысл производной.Рассмотрим график функции y = f ( x ):

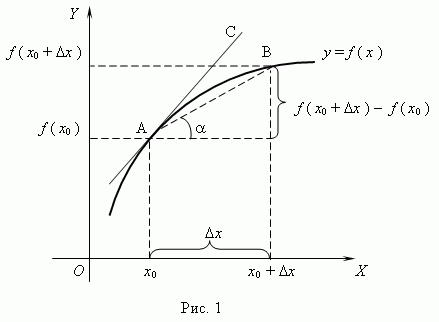
Из рис.1 видно, что для любых двух точек A и B графика функции:

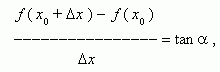
где - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.В этом и состоит геометрический смысл производной.

Уравнение касательной.Выведем уравнение касательной к графику функции в точке A ( x₀ , f ( x₀ ) ). В общем случае уравнение прямой с угловым коэффициентом f ’( x₀ ) имеет вид:

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда, b = f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо b, мы получим уравнение касательной:

y =f ( x₀ ) + f ’( x₀ ) · ( x – x₀ ) .

Механический смысл производной.Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t₀ до t₀ + точка перемещается на расстояние: x ( t₀ + ) x ( t₀ ) = , а её средняя скорость равна:v_a =  . При 0 значение средней скорости стремится к определённой величине, которая называетсямгновенной скоростью v ( t₀ ) материальной точки в момент времени t₀ . Но по определению производной мы имеем:

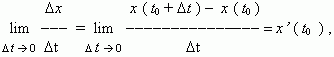
отсюда,v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).

8.Таблица производных и правила дифференцирования

О том, что такое производная, мы рассказали в статье «Геометрический смысл производной». Если функция задана графиком, её производная в каждой точке равна тангенсу угла наклона касательной к графику функции. А если функция задана формулой — вам помогут таблица производных и правила дифференцирования, то есть правила нахождения производной.

StudFiles.ru

§ 2. Определение производной.

Пусть функция y=f(x)определена на интервале (a;b). Рассмотрим значение аргумента(a;b). Дадим аргументу приращение∆x0, так чтобы выполнялось условие (x₀+∆x)a;b). Обозначим соответствующие значения функции через y₀иy₁:

y₀=f(x₀), y₁=f(x₀+∆x).При переходе отx₀кx₀+∆xфункция получит приращение

∆y = y₁- y₀ = f(x₀+∆x)-f(x₀).Если при стремлении∆xк нулю существует предел отношения приращения функции∆y к вызвавшему его приращению аргумента ∆x,

т.е. существует предел

= ,

то этот предел называется производной функции y=f(x)в точкеx₀. Итак, производная функцииy=f(x)в точкеx=x₀есть предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Производная функцииy=f(x)в точкеxобозначается символами(x) или(x). Используются также обозначения,,,. В последних трёх обозначениях подчёркивается то обстоятельство, что производная берётся по переменнойx.

Если функция y=f(x)имеет производную в каждой точке некоторого интервала, то на этом интервале производная(x) есть функция аргументаx.

§ 3. Механический и геометрический смысл производной.

Уравнения нормали и касательной к графику функции.

Как было показано в § 1, мгновенная скорость точки есть

v=.

Но это означает, что скорость vесть производная от пройденного путиSпо времениt,

v=. Таким образом, если функцияy=f(x)описывает закон прямолинейного движения материальной точки, гдеyесть путь, пройденный материальной точкой от момента начала движения до момента времениx, то производная(x) определяет мгновенную скорость точки в момент времениx. В этом и заключается механический смысл производной.

В § 1 был найден также угловой коэффициент касательной к графику функции y=f(x)k=tgα= . Это соотношение означает, что угловой коэффициент касательной равен производной(x). Говоря более строго, производная(x) функцииy=f(x), вычисленная при значении аргумента, равномx, равна угловому коэффициенту касательной к графику этой функции в точке, абсцисса которой равнаx. В этом состоит геометрический смысл производной.

Пусть при x=x₀функцияy=f(x)принимает значениеy₀=f(x₀), и график этой функции имеет касательную в точке с координатами (x₀;y₀). Тогда угловой коэффициент касательной

k = (x₀). Используя известное из курса аналитической геометрии уравнение прямой, проходящей через заданную точку в заданном направлении (y-y₀=k(x-x₀) ), запишем уравнение касательной:

Прямая, проходящая через точку касания перпендикулярно касательной, называется нормалью к кривой. Так как нормаль перпендикулярна касательной, то её угловой коэффициент k_нормсвязан с угловым коэффициентом касательнойkизвестным из аналитической геометрии соотношением:k_норм = ─, т.е. для нормали, проходящей через точку с координатами (x₀;y₀),k_норм= ─. Следовательно, уравнение этой нормали имеет вид:

(при условии, что).

§ 4. Примеры вычисления производной.

Для того чтобы вычислить производную функции y=f(x)в точкеx, необходимо:

- аргументу xдать приращение ∆x;

- найти соответствующее приращение функции ∆y=f(x+∆x) -f(x);

- составить отношение ;

- найти предел этого отношения при ∆x→0.

Пример 4.1. Найти производную функции y=C=const.

Аргументу xдаём приращение ∆ x.

Каково бы ни было x, ∆y=0: ∆y=f(x+∆x) ─f(x)=С─С=0;

Отсюда =0 и =0, т.е.=0.

Пример 4.2. Найти производную функции y=x.

∆ y=f(x+∆x) ─f(x)= x+∆x– x=∆ x;

=1, =1, т.е.=1.

Пример 4.3. Найти производную функции y=x2.

∆ y= (x+∆ x)2–x2= 2 x∙∆ x+ (∆ x)2;

= 2 x+ ∆ x, = 2 x, т.е.=2x.

Пример 4.4. Найти производную функции y=sinx.

∆ y=sin(x+∆x) – sin x = 2sincos(x+);

= ;

== cosx, т.е. = cos x.

Пример 4.5. Найти производную функции y=.

;

=, т.е.=.

StudFiles.ru

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t₀. К этому моменту точка прошла путь s=s(t₀). Определим скорость v материальной точки в момент времени t₀.

Для этого рассмотрим какой-нибудь другой момент времени t₀+Δt. Ему соответствует пройденный путь s=s(t₀+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t₀+Δt)–s(t).

Рассмотрим отношение 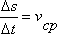. Оно называется средней скоростью в промежутке времени Δt. Средняя скорость не может точно охарактеризовать быстроту перемещения точки в моментt₀ (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt.

Итак, скоростью движения в данный момент времени t₀ (мгновенной скоростью) называется предел средней скорости в промежутке от t₀ до t₀+Δt, когда Δt→0:

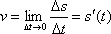т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

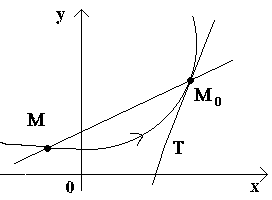
Пусть имеем кривую и на ней фиксированную точку М₀ (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M₀M. Если точка М начинает перемещаться по кривой, а точка М₀ остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М₀ с любой стороны секущая стремится занять положение определенной прямой М₀Т, то прямая М₀Тназывается касательной к кривой в данной точке М₀.

Т.о., касательной к кривой в данной точке М₀ называется предельное положение секущей М₀М, когда точка М стремится вдоль кривой к точкеМ₀.

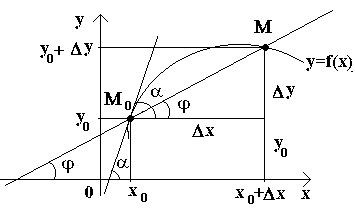Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х₀ функция принимает значение y₀=f(x₀). Этим значениям x₀ и y₀ на кривой соответствует точка М₀(x₀; y₀). Дадим аргументу x₀ приращение Δх. Новому значению аргумента соответствует наращенное значение функции y₀+Δ y=f(x₀–Δx). Получаем точку М(x₀+Δx; y₀+Δy). Проведем секущую М₀М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение 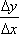и заметим, что .

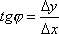Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М₀. Тогда секущая М₀М будет стремиться занять положение касательной к кривой в точке М₀, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

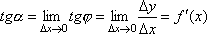
т.е. f '(x) = tg α .

Т.о., геометрически у '(x₀) представляет угловой коэффициент касательной к графику этой функции в точке x₀, т.е. при данном значении аргумента x, производная равна тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке М₀ (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х2 в точке М(-1; 1).

Ранее мы уже видели, что (x2)' = 2х. Но угловой коэффициент касательной к кривой есть tg α = y'|_x=-1 = – 2.

studopedia.ru

Геометрический, механический, экономический смыл производной

Определение производной.

Лекция №7-8

Список используемой литературы

1 Ухоботов, В. И. Математика: Учебное пособие.- Челябинск: Челяб. гос. ун-т, 2006.- 251 с.

2 Ермаков, В.И. Сборник задач по высшей математике. Учебное пособие. –М.: ИНФРА-М, 2006. – 575 с

3 Ермаков, В.И. Общий курс высшей математики. Учебник. –М.: ИНФРА-М, 2003. – 656 с.

Тема «Производная»

Цель:объяснить понятие производной, проследить зависимость междунепрерывностью и дифференцируемостью функции, показать применимость использования производной на примерах.

Ключевые слова: производная, приращение аргумента, приращение функции.

Вопросы:

1.Определение производной. Геометрический, механический, экономический смысл производной.

2.Зависимость между непрерывностью и дифференцируемостью функции.

3.Вычисление производной. Основные правила дифференцирования.

4.Основные формулы дифференцирования. Таблица производных.

Пусть y=f(x) непрерывная функция от х. Дадим аргументу х приращение 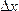, тогда функция y получит приращение 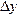. Составим отношение 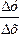. Это отношение есть некоторая функция от 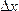. Может случиться, что эта функция имеет предел при 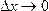, т.е. существует

Этот предел называется производной от данной функции yи обычно обозначается через 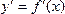или. .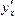

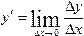Отсюда вытекает такое определение:

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Обозначение 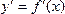ввел Лагранж,

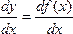Лейбниц, Ньютон.

Геометрический смысл производной: для данной функции y=f(x) ее производная 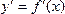для каждого значения х равна угловому коэффициенту касательной к графику функции в соответствующей точке.

Физический смысл производной: для функции 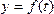, меняющейся со временем t, производная 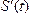есть скорость изменения функции S в данный момент t.

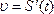Экономический смысл производной: пусть предприятие выпускает однородную продукцию. Тогда издержки производства y можно считать функцией количества выпускаемой продукции x, y=f(x).

Предположим, что количество выпускаемой продукции изменилось на 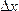, тогда издержки производства изменяются на .

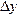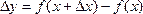Разделим приращение издержек производства на приращение выпускаемой продукции

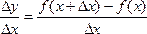(1).

Это равенство выражает среднее приращение издержек производства на единицу приращенной продукции, перейдем к пределy:

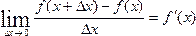Этот предел в экономике называется предельными издержками производства.

studopedia.ru

Определение производной. Геометрический и механический смысл производной, уравнение касалельной к графику функции.

Нужен краткий ответ (без лишней воды)

Мертвый_белый_снег

Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции.
Геометрический?
Касательная к функции в точке... .
Условие возрастания функции: f ' (x) > 0.
Условие убывания функции: f ' (x) < 0.
Точка перегиба (необходимое условие) : f ' ' (x0) = 0.
Выпуклость вверх: f ' ' (x) Выпуклость вниз: f ' ' (x) >0
Уравнение нормали: у=f(x0)-(1/f `(x0))(x-x0)
Механический?
скорость это производная по расстоянию, ускорение производная по скорости и вторая производна по расстоянию.. .
Уравнение касательной к графику функции f в точке x0
y=f(x0)+f `(x0)(x-x0)

Пользователь удален

Если сеществует предел отношения дельта y к дельта x приращения функции дельта y к вызвавшему его приращению аргумента дельта x, когда дельта x стремиться к нулю, то этот предел называется производной функции y = f(x) в данной точке х и обозначается y' или f'(x)
Скорость v прямолинейного движения есть производная пути s по времени t: v = ds/dt. В этом состоит механический смысл производной.
Угловои коэффициент касательной к кривой y = f(x) в точке с абсциссой х нулевое есть производная f'(x нулевого). В этом состоит геометрический смысл производной.
Касательной кривой в точке М нулевое называется прямая М нулевое Т, угловой коэффициент которой равен пределу углового коэффициента секущей М нулевое М один, когда дельта х стремится к нулю.
tg фи = lim tg альфа при дельта х стремится к нулю = lim (дельта х/ дельта у) при дельта х стремится к нулю
Из геометрического смысла производной уравнение касательной примет вид:
у - у нулевое = f'(x нулевого)(х - х нулевое)