Среднее арифметическое
У этого термина существуют и другие значения, см. среднее значение.Сре́днее арифмети́ческое (в математике и статистике) множества чисел — сумма всех чисел, делённая на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ {\displaystyle {\bar {x}}} , произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и x ¯ {\displaystyle {\bar {x}}} в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда x ¯ {\displaystyle {\bar {x}}} (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + ⋯ + x n ) . {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n}).}Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры
- Для трёх чисел необходимо сложить их и разделить на 3:
- Для четырёх чисел необходимо сложить их и разделить на 4:
Или проще 5+5=10, 10:2. Потому что мы складывали 2 числа, а значит, сколько чисел складываем, на столько и делим.
Непрерывная случайная величина
Для непрерывно распределённой величины f ( x ) {\displaystyle f(x)} среднее арифметическое на отрезке [ a ; b ] {\displaystyle [a;b]} определяется через определённый интеграл:
f ( x ) ¯ [ a ; b ] = 1 b − a ∫ a b f ( x ) d x {\displaystyle {\overline {f(x)}}_{[a;b]}={\frac {1}{b-a}}\int _{a}^{b}f(x)dx}Некоторые проблемы применения среднего
Отсутствие робастности
Основная статья: Робастность в статистикеХотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Основная статья: Окупаемость инвестицийЕсли числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года всего на $5.1, средний рост в 8,2 % даёт конечный результат $35.1:
[$30 (1 — 0.1) (1 + 0.3) = $30 (1 + 0.082) (1 + 0.082) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: [$30 (1 + 0.1) (1 + 0.1) = $36.3].
Сложный процент в конце 2 года: 90 % * 130 % = 117 % , то есть общий прирост 17 %, а среднегодовой сложный процент 117 % ≈ 108.2 % {\displaystyle {\sqrt {117\%}}\approx 108.2\%} , то есть среднегодовой прирост 8,2 %.
Направления
Основная статья: Статистика направленийПри расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 1 ∘ + 359 ∘ 2 = {\displaystyle {\frac {1^{\circ }+359^{\circ }}{2}}=} 180°. Это число неверно по двум причинам.
- Во-первых, угловые меры определены только для диапазона от 0° до 360° (или от 0 до 2π при измерении в радианах). Таким образом, ту же пару чисел можно было бы записать как (1° и −1°) или как (1° и 719°). Средние значения каждой из пар будут отличаться: 1 ∘ + ( − 1 ∘ ) 2 = 0 ∘ {\displaystyle {\frac {1^{\circ }+(-1^{\circ })}{2}}=0^{\circ }} , 1 ∘ + 719 ∘ 2 = 360 ∘ {\displaystyle {\frac {1^{\circ }+719^{\circ }}{2}}=360^{\circ }} .
- Во-вторых, в данном случае, значение 0° (эквивалентное 360°) будет геометрически лучшим средним значеним, так как числа отклоняются от 0° меньше, чем от какого-либо другого значения (у значения 0° наименьшая дисперсия). Сравните:
- число 1° отклоняется от 0° всего на 1°;
- число 1° отклоняется от вычисленного среднего, равного 180°, на 179°.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
ru.wikipedia.org
Среднее значение
Сре́днее значе́ние — числовая характеристика множества чисел или функций (в математике); — некоторое число, заключённое между наименьшим и наибольшим из их значений.
Основные сведения
Исходным пунктом становления теории средних величин явилось исследование пропорций школой Пифагора. При этом не проводилось строгого различия между понятиями средней величины и пропорции. Значительный толчок развитию теории пропорций с арифметической точки зрения был дан греческими математиками — Никомахом Герасским (конец I — начало II в. н. э.) и Паппом Александрийским (III в. н. э.). Первым этапом развития понятия средней является этап, когда средняя стала считаться центральным членом непрерывной пропорции. Но понятие средней как центрального значения прогрессии не даёт возможности вывести понятие средней по отношению к последовательности n членов, независимо от того, в каком порядке они следуют друг за другом. Для этой цели необходимо прибегнуть к формальному обобщению средних. Следующий этап — переход от непрерывных пропорций к прогрессиям — арифметической, геометрической и гармонической (англ.)[1].
В истории статистики впервые широкое употребление средних величин связано с именем английского учёного У. Петти. У. Петти один из первых пытался придать средней величине статистический смысл, связав её с экономическими категориями. Но описания понятия средней величины, его выделения, Петти не произвёл. Родоначальником теории средних величин принято считать А. Кетле. Он одним из первых начал последовательно разрабатывать теорию средних величин, пытаясь подвести под неё математическую базу. А. Кетле выделял два вида средних величин — собственно средние и средние арифметические. Собственно средние представляют вещь, число, действительно существующие. Собственно средние или средние статистические должны выводиться из явлений однокачественных, одинаковых по своему внутреннему значению. Средние арифметические — числа, дающие возможно близкое представление о многих числах, различных, хотя и однородных[2].
Каждый из видов средней может выступать либо в форме простой, либо в форме взвешенной средней. Правильность выбора формы средней вытекает из материальной природы объекта исследования. Формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются. Когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторений индивидуальных значений признака присутствует в расчётных формулах степенных средних. В этом случае они называются формулами взвешенных средних.[3]
Иерархия средних значений в математике
- среднее значение функции — понятие, определяемое многими способами.
- Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
- среднее степенное — частный случай средних Колмогорова при ϕ ( x ) = x α {\displaystyle \phi (x)=x^{\alpha }} . Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
- среднее арифметическое ( α = 1 {\displaystyle \alpha =1} );
- среднее квадратическое ( α = 2 {\displaystyle \alpha =2} );
- среднее гармоническое ( α = − 1 {\displaystyle \alpha =-1} );
- по непрерывности при α → 0 {\displaystyle \alpha \to 0} доопределяется среднее геометрическое, которое также является Колмогоровским средним при ϕ ( x ) = log x {\displaystyle \phi (x)=\log x}
- среднее степенное — частный случай средних Колмогорова при ϕ ( x ) = x α {\displaystyle \phi (x)=x^{\alpha }} . Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
- Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
- Среднее взвешенное — обобщение средней величины на случай произвольной линейной комбинации:
- Среднее арифметическое взвешенное.
- Среднее геометрическое взвешенное.
- Среднее гармоническое взвешенное.
- среднее хронологическое — обобщает значения признака для одной и той же единицы или совокупности в целом, изменяющихся во времени.
- среднее логарифмическое, определяемое по формуле a ¯ = a 1 − a 2 ln ( a 1 / a 2 ) {\textstyle {\bar {a}}={\frac {a_{1}-a_{2}}{\ln(a_{1}/a_{2})}}} , используется в теплотехнике
- среднее логарифмическое, определяемое в электроизоляции соответствии с ГОСТ 27905.4-88 определяется как l o g a ¯ = log a 1 + l o g a 2 + . . . + . . . l o g a n a 1 + a 2 + . . . + a n {\textstyle log{\bar {a}}={\frac {\log a_{1}+loga_{2}+...+...loga_{n}}{a_{1}+a_{2}+...+a_{n}}}} (логарифм по любому основанию)[4]
В теории вероятностей и статистике
Основная статья: Показатели центра распределения- непараметрические средние — мода, медиана.
- среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.
ru.wikipedia.org
Символ
У этого термина существуют и другие значения, см. Символ (значения).Си́мвол (др.-греч. σύμβολον — «(условный) знак, сигнал») — это знак, изображение какого-нибудь предмета или животного, для обозначения качества объекта[1]; условный знак каких-либо понятий, идей, явлений 2.
Иногда знак и символ различаются, поскольку, в отличие от знака, символу приписывают более глубокое социально-нормативное (духовное) измерение[2][3].
История
Понятие символа тесно соприкасается с такими категориями, как художественный образ, аллегория и сравнение. Например, в эпоху поздней античности крест стал символом христианства[4][неавторитетный источник?]. В новейшее время свастика стала символом национал-социализма.
Ф. И. Гиренок обращал внимание, что в современной культуре стерта разница «между знаком и символом», между тем как спецификой символа является указание на сверхреальное[5].
А. Ф. Лосев определял символ как «субстанциальное тождество идеи и вещи»[6]. Всякий символ заключает в себе образ, но не сводится к нему, поскольку подразумевает присутствие некоего смысла, нераздельно слитого с образом, но ему не тождественного. Образ и смысл образуют два элемента символа, немыслимые друг без друга. Посему символы существуют как символы (а не как вещи) только внутри интерпретаций[7].
В XX веке неокантианец Кассирер обобщил понятие символа и отнес к «символическим формам» широкий класс культурных явлений, таких как язык, миф, религия, искусство и наука, посредством которых человек упорядочивает окружающий его хаос. Ранее ещё Кант доказывал, что искусство, будучи интуитивным способом представления, носит символический характер[8].
ru.wikipedia.org
Подскажите значение данного символа.
Интересует что конкретно означает пентаграмма вписанная в круг солнечных лучей

Дядя никита
Почитав ответы других, сразу видно что люди видят в пентаграмме сразу же символ Дьявола ))) Люди не хотят знать, их страх перед сатаной заменяет им знания.
Пентаграмма, а ещё и в кругу - древний защитный знак. И правильная пентаграмма стоит на двух концах. Как я вижу на картинке, никакой перевернутой пентаграммы на картинке нет. Просто стилизировали простую пентаграмму в круге, чем-то типа лучей, щупалец, пламенем (?)
По идее это даже не только защитный знак, но ещё и символ победы духовного над материальным. Это четыре алхимических элемента, плюс эфир.
А перевернутая пентаграмма как раз символизирует наоборот - победу материального над духовным. И вообще, нельзя путать Сатанизм с Дьяволопоклонничеством. Это две разные вещи и люди любят грести всё под одну гребёнку, потому что у них нет знаний, а есть страхи, домыслы, догадки и фантазии.
Lonesome crow
Самый знаменитый маг XX века Алистер Кроули трактовал перевернутую пентаграмму как представленный в виде солнечных лучей дух, который оживляет материю-Землю. Другие эзотерики утверждают, что перевернутая пентаграмма изливает энергию с неба на землю и, следовательно, является символом материалистических тенденций, тогда как обычная пентаграмма направляет энергию вверх, являясь символом духовных исканий человечества.
Lar_ka
Ой, у масонов так много разных символов.. .
Скорее всего, это нечто каббалистическое.
И зачем вы сатанинскими символами интересуетесь-то? ! Выбросьте его из головы - и дело с концом, как говорится.
Читайте также
![Символ медицины чаша со змеей значение Символ медицины чаша со змеей значение]() Символ медицины чаша со змеей значение
Символ медицины чаша со змеей значение![Расчет среднего значения Расчет среднего значения]() Расчет среднего значения
Расчет среднего значения![Обозначение среднего значения Обозначение среднего значения]() Обозначение среднего значения
Обозначение среднего значения![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского- 7 Треф значение
![Славянские имена мальчиков и их значение Славянские имена мальчиков и их значение]() Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия![Амбициозный значение слова Амбициозный значение слова]() Амбициозный значение слова
Амбициозный значение слова![Старинные русские слова и их значение Старинные русские слова и их значение]() Старинные русские слова и их значение
Старинные русские слова и их значение![Амир значение имени характер и судьба Амир значение имени характер и судьба]() Амир значение имени характер и судьба
Амир значение имени характер и судьба![Балда значение слова Балда значение слова]() Балда значение слова
Балда значение слова
 Символ медицины чаша со змеей значение
Символ медицины чаша со змеей значение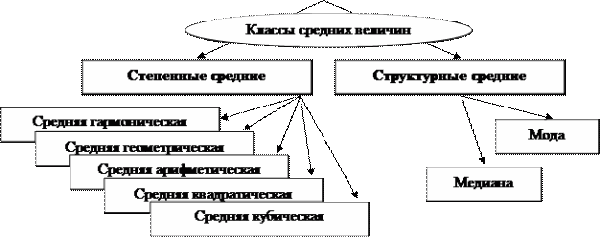 Расчет среднего значения
Расчет среднего значения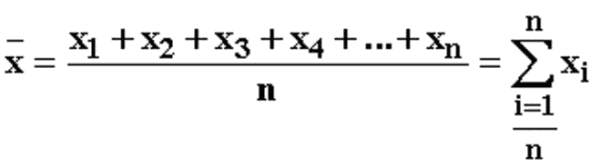 Обозначение среднего значения
Обозначение среднего значения Аутентичность значение слова
Аутентичность значение слова Чувак значение слова с еврейского
Чувак значение слова с еврейского Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение Барыга значение слова википедия
Барыга значение слова википедия Амбициозный значение слова
Амбициозный значение слова Старинные русские слова и их значение
Старинные русские слова и их значение Амир значение имени характер и судьба
Амир значение имени характер и судьба Балда значение слова
Балда значение слова