Область значений это:
Область значений Запрос «Отображение» перенаправляется сюда. Cм. также другие значения.В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
|
Определения
- Нестрогое определение: функция — это «закон», по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
- Строгое определение: функция или отображе́ние — это бинарное отношение, обладающее свойством:
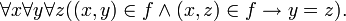
- Функция называется инъективной, если

Обозначения
 ,
,  или
или  для отображения F множества X в множество Y;
для отображения F множества X в множество Y;
- Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или
 .).
.). - Множество Y называется о́бластью значе́ний отображения F.(обозначается E(F), или
 ).
).
- Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или
 , y = F(x) или
, y = F(x) или  или
или  . Используется также обратная польская запись: y = xF, а иногда y = xF.
. Используется также обратная польская запись: y = xF, а иногда y = xF.
- Элементы x называют аргументами функции, а соответствующие элементы y — значениями функции.
Связанные определения
- Пусть дано отображение
 , и
, и  . Тогда суже́нием функции F на M называется функция
. Тогда суже́нием функции F на M называется функция  , определяемая равенством
, определяемая равенством  . Это определение подчёркивает, что фиксация области определения является частью определения функции.
. Это определение подчёркивает, что фиксация области определения является частью определения функции.
- F является продолжением функции
 на множество
на множество  . Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
. Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
- Пусть
 . Тогда о́бразом множества M называется подмножество множества Y, определяемое равенством
. Тогда о́бразом множества M называется подмножество множества Y, определяемое равенством  .
.
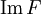 .
.
- Пусть задано отображение
 ,
,  и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент
и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент  должен иметь ровно один образ, но элемент
должен иметь ровно один образ, но элемент  может не иметь прообразов либо иметь один или несколько.
может не иметь прообразов либо иметь один или несколько.
- Например, пусть дана функция
 , где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
, где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
- Например, пусть дана функция
- Пусть задано отображение
 , и
, и  . Тогда множество
. Тогда множество  называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
- Например, пусть
 , и F(x) = sinx. Тогда
, и F(x) = sinx. Тогда  .
.
- Например, пусть
- Пусть
 . Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством
. Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством  .
.
- Например, пусть
 , и F(x) = cosx. Тогда
, и F(x) = cosx. Тогда ![F\left(\left[0,\;\frac{\pi}{2}\right]\right)=[0,\;1]](data:image/gif;base64,R0lGODdhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=) ,
, ![F^{-1}([0,\;1])=\bigcup\limits_{n\in\Z}\left[-\frac{\pi}{2}+2\pi n,\;\frac{\pi}{2}+2\pi n\right]](data:image/gif;base64,R0lGODdhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=) .
.
- Например, пусть
Свойства
Свойства прообразов и образов
 ;
; ;
; ;
; . Заметим отсутствие равенства в этом случае.
. Заметим отсутствие равенства в этом случае.
Классы функций
При необходимости можно различать отображения в зависимости от природы множеств X и Y. Если X и Y — числовые множества, такие, как 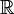 или
или 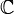 , то отображение называют функцией. Если X или Y многомерны, например,
, то отображение называют функцией. Если X или Y многомерны, например, 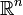 или
или 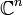 , то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
, то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
Вариации и обобщения
- многозначная функция
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Пусть даны множества 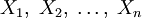 и множество Y, тогда упорядоченное множество всех кортежей
и множество Y, тогда упорядоченное множество всех кортежей 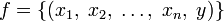 называется функцией n аргументов тогда и только тогда, когда для любых
называется функцией n аргументов тогда и только тогда, когда для любых 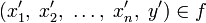 и
и 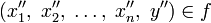 из
из 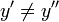 следует, что
следует, что ![x_{n}' \neq x_{n}'',\forall x\in [1,\;n]\cap\Z](http://i.zna4enie.ru/3/kak-oboznachaetsja-oblast-opredelenija-funkcii_40.png) .[1]
.[1]
Примечания
- ↑ Кудрявцев Л. Д. Курс математического анализа. — том 1. — М.: Высшая школа, 1981. — с. 8.
См. также
- Композиция функций
- График функции
- Сюръективность
- Инъективность
- Биективность
- Функция с множеством значений {0, 1}
- Функциональное уравнение
Литература
- Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Wikimedia Foundation. 2010.
dic.academic.ru
Область определения функции
Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Определение
Если на множестве X {\displaystyle X} задана функция, которая отображает множество X {\displaystyle X} в другое множество, то множество X {\displaystyle X} называется областью определения или областью задания функции.
Более формально, если задана функция f {\displaystyle f} , которая отображает множество X {\displaystyle X} в Y {\displaystyle Y} , то есть: f : X → Y {\displaystyle f\colon X\to Y} , то
- множество X {\displaystyle X} называется областью определения[1] или областью задания[2] функции f {\displaystyle f} и обозначается D ( f ) {\displaystyle D(f)} или d o m f {\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).
Иногда рассматривают функции, определенные на подмножестве D {\displaystyle D} некоторого множества X {\displaystyle X} . В этом случае множество X {\displaystyle X} иногда называют областью отправления функции f {\displaystyle f} [3].
Примеры
Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.
Числовые функции
Числовые функции — это функции, относящиеся к следующим двум классам:
- вещественнозначные функции вещественного переменного — это функции вида f : R → R {\displaystyle f\colon \mathbb {R} \to \mathbb {R} } ;
- а также комплекснозначные функции комплексного переменного вида f : C → C {\displaystyle f\colon \mathbb {C} \to \mathbb {C} } ,
где R {\displaystyle \mathbb {R} } и C {\displaystyle \mathbb {C} } — множества вещественных и комплексных чисел соответственно.
Тождественное отображение
Область определения функции f ( x ) = x {\displaystyle f(x)=x} совпадает с областью отправления ( R {\displaystyle \mathbb {R} } или C {\displaystyle \mathbb {C} } ).
Гармоническая функция
Область определения функции f ( x ) = 1 / x {\displaystyle f(x)=1/x} представляет собой комплексную плоскость без нуля:
d o m f = C ∖ { 0 } {\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}} ,поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.
Дробно-рациональные функции
Область определения функции вида
f ( x ) = a 0 + a 1 x + ⋯ + a m x m b 0 + b 1 x + ⋯ + b n x n {\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}}представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения
b 0 + b 1 x + ⋯ + b n x n = 0 {\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0} .Эти точки называются полюсами функции f {\displaystyle f} .
Так, например, f ( x ) = 2 x x 2 − 4 {\displaystyle f(x)={\frac {2x}{x^{2}-4}}} определен на всех точках, где знаменатель не обращается в ноль, то есть, где x 2 − 4 ≠ 0 {\displaystyle x^{2}-4\neq 0} . Таким образом d o m f {\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и -2.
Мера
Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.
Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.
Например, определённый интеграл представляет собой функцию ориентированного промежутка.
Функционал
Пусть F = { f ∣ f : X → R } {\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}} — семейство отображений из множества X {\displaystyle X} в множество R {\displaystyle \mathbb {R} } . Тогда можно определить отображение вида F : F → R {\displaystyle F\colon \mathbb {F} \to \mathbb {R} } . Такое отображение называется функционалом.
Если, например, фиксировать некоторую точку x 0 ∈ X {\displaystyle x_{0}\in ~X} , то можно определить функцию F ( f ) = f ( x 0 ) {\displaystyle F(f)=f(x_{0})} , которая принимает в «точке» f {\displaystyle f} то же значение, что и сама функция f {\displaystyle f} в точке x 0 {\displaystyle x_{0}} .
ru.wikipedia.org
Область (значения) это:
Область (значения) В Викисловаре есть статья «область»
В Викисловаре есть статья «область»
О́бласть — некоторая часть большей структуры. Термин о́бласть может означать:
В географии- Административная область
- Область (административная единица) — единица федерального деления в России или административно-территориального деления в ряде других стран.
- Зоогеографическая область — регион Земли, выделяющийся особенностями фаунистического состава.
- Историческая область — территория, составлявшая в исторической ретроспективе политическое единство.
- Историко-культурная область — территория с исторически сложившимися сходными культурно-бытовыми особенностями населения.
- Физико-географическая область — часть физико-географической страны, расположенная в пределах одной природной зоны и имеющая морфоструктурную и литологическую однородность.
- Область (топология) — открытое связное подмножество.
См. также
- Домен (область)
| Cписок значений слова или словосочетания со ссылками на соответствующие статьи. Если вы попали сюда из другой статьи Википедии, пожалуйста, вернитесь и уточните ссылку так, чтобы она указывала на статью. |
- Многозначные термины
Wikimedia Foundation. 2010.
dic.academic.ru
Как найти область определения и область значения функции x+8/x-4
Артур ройспих
а хрен знает) ну или вот )))))))))))))
.
одно из важнейших математических
понятий. Напомним, что функцией называют та-
кую зависимость переменной у от переменной х,
при которой каждому значению переменной х
соответствует единственное значение перемен-
ной у.
Переменную х называют независимой переменной
или аргументом. Переменную у называют зависимой
переменной. Говорят также, что переменная у явля-
ется функцией от переменной х. Значения зависи-
мой переменной называют значениями функции.
Если зависимость переменной у от переменной х
является функцией, то коротко это записывают
так: y=f(x). (Читают: у равно f от х. ) Символом
f(x) обозначают значение функции, соответствую-
щее значению аргумента, равному х.
Пусть, например, функция задается формулой
у=2х2 - 6. Тогда можно записать, что f(x) = 2х2 - 6.
Найдем значения функции для значений х, равных,
например, 1, 2,5, -3, т. е. найдем f(1), f (2,5), f(-3):
f(1) = 2 • 1 2 - 6 = - 4;
f(2,5) = 2 • 2,52 - 6 = 6,5;
f(-3) = 2 • (-3)2-6 = 12.
- 3 -
Все значения независимой переменной образу-
ют область определения функции. Все значения,
которые принимает зависимая переменная, образу-
ют область значений функции.
Если функция задана формулой и ее область оп-
ределения не указана, то считают, что область оп-
ределения функции состоит из всех значений аргу-
мента, при которых формула имеет смысл. Напри-
мер, областью определения функции f (х) = 5х + х2
является множество всех чисел; областью определе-
Рис. 1
чисел, кроме -3.
Область определения функции, описывающей
реальный процесс, зависит от конкретных условий
его протекания. Например, зависимость длины I
железного стержня от температуры нагревания t
выражается формулой l = l0(1 + at), где l0 — на-
чальная длина стержня, а а — коэффициент ли-
нейного расширения. Указанная формула имеет
смысл при любых значениях t. Однако областью
определения функции l = f(t) является промежуток
в несколько десятков градусов, для которого спра-
ведлив закон линейного расширения.
Напомним, что графиком функции называют
множество всех точек координатной плоскос-
ти, абсциссы которых равны значениям аргу-
мента, а ординаты — соответствующим зна-
чениям функции.
На рисунке 1 изображен график
функции у = f(x), областью определе-
ния которой является промежуток
[-3; 7]. С помощью графика можно
найти, например, что f(-3) = -2,
f(0) = 2,5, f(2) = 4, f(5) = 2. Наи-
меньшее значение функции равно -2,
а наибольшее равно 4; при этом лю-
бое число от -2 до 4 является значе-
нием данной функции. Таким обра-
зом, областью значений функции
y = f(x) служит промежуток [-2; 4].
Мы изучили некоторые важные виды функций:
линейную функцию, т. е. функцию, задаваемую
формулой у =kx - b, где k и b — некоторые числа;
прямую пропорциональность — частный случай
линейной функции, она задается формулой y=kx
- 4 -
Рис. 2
Рис. 3
б)
Графиком функции y = kx + b слу-
жит прямая (рис. 2). Ее областью
определения является множество
всех чисел. Область значений этой
ласть
Читайте также
![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского- 7 Треф значение
![Славянские имена мальчиков и их значение Славянские имена мальчиков и их значение]() Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия![Амбициозный значение слова Амбициозный значение слова]() Амбициозный значение слова
Амбициозный значение слова![Старинные русские слова и их значение Старинные русские слова и их значение]() Старинные русские слова и их значение
Старинные русские слова и их значение![Амир значение имени характер и судьба Амир значение имени характер и судьба]() Амир значение имени характер и судьба
Амир значение имени характер и судьба![Балда значение слова Балда значение слова]() Балда значение слова
Балда значение слова![Бит может принимать значения Бит может принимать значения]() Бит может принимать значения
Бит может принимать значения![Тимур значение имени характер Тимур значение имени характер]() Тимур значение имени характер
Тимур значение имени характер![Города федерального значения россии список Города федерального значения россии список]() Города федерального значения россии список
Города федерального значения россии список
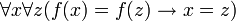
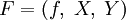 ,
, 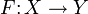 или
или 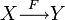 для отображения F множества X в множество Y;
для отображения F множества X в множество Y;
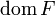 .).
.).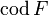 ).
). , y = F(x) или
, y = F(x) или 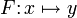 или
или 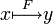 . Используется также обратная польская запись: y = xF, а иногда y = xF.
. Используется также обратная польская запись: y = xF, а иногда y = xF.
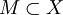 . Тогда суже́нием функции F на M называется функция
. Тогда суже́нием функции F на M называется функция 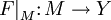 , определяемая равенством
, определяемая равенством 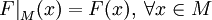 . Это определение подчёркивает, что фиксация области определения является частью определения функции.
. Это определение подчёркивает, что фиксация области определения является частью определения функции.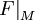 на множество
на множество 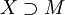 . Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
. Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.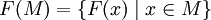 .
.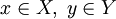 и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент
и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент 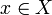 должен иметь ровно один образ, но элемент
должен иметь ровно один образ, но элемент 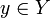 может не иметь прообразов либо иметь один или несколько.
может не иметь прообразов либо иметь один или несколько.
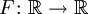 , где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
, где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.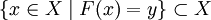 называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
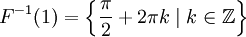 .
.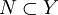 . Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством
. Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством 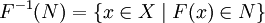 .
.
![F\left(\left[0,\;\frac{\pi}{2}\right]\right)=[0,\;1]](http://i.zna4enie.ru/e/kak-oboznachaetsja-oblast-opredelenija-funkcii_25.png) ,
, ![F^{-1}([0,\;1])=\bigcup\limits_{n\in\Z}\left[-\frac{\pi}{2}+2\pi n,\;\frac{\pi}{2}+2\pi n\right]](http://i.zna4enie.ru/b/kak-oboznachaetsja-oblast-opredelenija-funkcii_26.png) .
.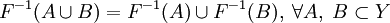 ;
;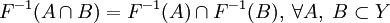 ;
;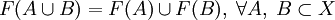 ;
;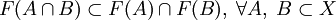 . Заметим отсутствие равенства в этом случае.
. Заметим отсутствие равенства в этом случае. Аутентичность значение слова
Аутентичность значение слова Чувак значение слова с еврейского
Чувак значение слова с еврейского Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение Барыга значение слова википедия
Барыга значение слова википедия Амбициозный значение слова
Амбициозный значение слова Старинные русские слова и их значение
Старинные русские слова и их значение Амир значение имени характер и судьба
Амир значение имени характер и судьба Балда значение слова
Балда значение слова Бит может принимать значения
Бит может принимать значения Тимур значение имени характер
Тимур значение имени характер Города федерального значения россии список
Города федерального значения россии список