Что такое система счисления?
|
Система счисления— это совокупность приемов и правил, по которым числа записываются и читаются. |
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7. 102 + 5. 101 + 7. 100 + 7. 10—1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
|
Основание позиционной системы счисления— количество различных цифр, используемых для изображения чисел в данной системе счисления. |
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1qn-1+ an-2qn-2+ ... + a1q1+ a0q0+ a-1q-1+ ... + a-mq-m,
где ai — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно. Например:
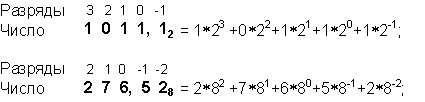
Какие системы счисления используют специалисты для общения с компьютером?
Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
-
двоичная (используются цифры 0, 1);
-
восьмеричная (используются цифры 0, 1, ..., 7);
-
шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:
|
|
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.
StudFiles.ru
Понятие системы счисления
 Системой счисления (или нумерацией) называют совокупность приёмов построения, обозначения и наименования чисел. Каждая система счисления включает:
Системой счисления (или нумерацией) называют совокупность приёмов построения, обозначения и наименования чисел. Каждая система счисления включает:
1) определённый набор символов (цифр) для записи чисел; эти символы составляют конечный алфавит;
2) определённый способ чтения (наименования) чисел.
Каждой цифре в записи числа однозначно сопоставляется количество, выражаемое этой цифрой. Это количество будем называть количественным эквивалентом цифры[1].
По способу определения количественного эквивалента цифры в записи числа все системы счисления можно разбить на два класса: непозиционные и позиционные.
 Система счисления называется непозиционной, если каждой цифре и в любом месте в записи числа однозначным образом сопоставлен некоторый количественный эквивалент. Таким образом, в непозиционных системах счисления местоположение цифры в записи числа (позиция) не влияет на её количественный эквивалент.
Система счисления называется непозиционной, если каждой цифре и в любом месте в записи числа однозначным образом сопоставлен некоторый количественный эквивалент. Таким образом, в непозиционных системах счисления местоположение цифры в записи числа (позиция) не влияет на её количественный эквивалент.
Примером непозиционной системы счисления является римская система[2]. Количественные эквиваленты цифр римской системы счисления равны: (I) = l; (V) = 5; (X) = 10; (L) = 50; (С) = 100; (D) = 500; (М) = 1000.
Количественный эквивалент числа в римской системе счисления определяется по следующему правилу: если в записи числа слева от символа находится символ, имеющий не меньший количественный эквивалент, то этот количественный эквивалент включается в сумму со знаком «плюс», в противном случае - со знаком «минус». Например,количественные эквиваленты чисел CCXXXIX и DCCXL равны: …….(CCXXXIX) = 10 - 1 + 10 + 10 + 10 + 100 + 100 = 239,
(DCCXL) = 50 –10 + 100 + 100 + 500 = 740.
Исторически вначале появились непозиционные системы счисления. Общим недостатком этих систем счисления является трудность записи в них больших чисел: либо эти записи слишком громоздки, либо алфавит цифр весьма велик. Именно поэтому непозиционные системы счисления в вычислительной технике практически не нашли применения.
 Система счисления называется позиционной, если количественный эквивалент цифры определяется не только видом самой цифры, но и её местоположением в записи числа - позицией.
Система счисления называется позиционной, если количественный эквивалент цифры определяется не только видом самой цифры, но и её местоположением в записи числа - позицией.
Примером такой системы является широко используемая нами десятичная система. При смене позиции (места) цифры в числе меняется её количественный эквивалент. Например, у числа 333,3 первая цифра справа означает «три десятых долей единицы», вторая «три единицы», третья – «три десятка», а четвёртая – «три сотни». Сама же запись 333,3 означает сокращённую запись выражения 300 + 30 + + 3 + 0,3 = 3×102 + 3×101 + 3×100 + 3×10 –1 = 333,3.
Любая позиционная система счисления характеризуется своим основанием.
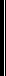 Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание системы можно принять любое натуральное число – два, три, четыре и т.д.
Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание системы можно принять любое натуральное число – два, три, четыре и т.д.
Наиболее широкое использование имеют следующие системы счисления:
· десятичная (используются цифры 0, 1, 2, ..., 9);
· двоичная (используются цифры 0, 1);
· восьмеричная (используются цифры 0, 1, 2, ..., 7);
· шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, 2, ..., 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).
Любое число А в позиционной системе счисления можно записать в общем виде[3]:
А(p) = 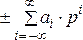 ,
,
где ai – цифра в i-том разряде записи числа в системе счисления с основанием р.
Для определения номера разряда (значения i) используется простое правило (см. рис. 4.7): первый слева от запятой разряд (точка отсчёта) является нулевым; номера остальных разрядов равны их порядковому номеру относительно нулевого разряда: влево (целая часть числа) – со знаком «+» (при записи опускается); вправо (дробная часть числа) – со знаком «–». Например,
324,54(10) = 3×102 + 2×101 + 4×100 + 5×10–1 + 4×10–2,
1101,01(2) = 1×23 + 1×22 + 0×21 +1×20 + 0×2–1 + 1×2–2,
352,51(8) = 3×82 + 5×81 + 2×80 + 5×8-1 + 1×8–2,
A4C,3F(16) = 10×162 + 4×161 + 12×160 + 3×16–1 + 15×16–2.

Рис. 4.7. Принцип нумерации разрядов записи числа
studopedia.ru
Обсуждение:Система счисления
СОК
Вот какой вопрос... как и где используют СОК (систему остаточных классов), ну например, при построении всяческих электронных систем?! и вот ещё... при разработке разных сумматоров, множительных устройств, вычитательных и тому подобных, я столкнулся с тем, что часто употребляется фраза типа - такое-то устройство относиться к области выч. техники и электроники и может быть использовано для построения средств аппаратурного контроля и цифровых устройств, работающих в системе остаточных классов. Как растолковать сие предложение?! Неужели эта область настолько распространена и востребована в мире, что в ней происходит постоянное патентообновление?! или это просто отголоски прошлого и в принцыпе это бесперспективное занятие, я имею ввиду изобретение всё более и более простых выч. устройст как в унитарных так и в позиционных кодах. Понятно, что тежи суматоры используют, да пускай даже, для постороения таймеров и тому подобных, я уже не говорю о более сложных системах, но неужели имеет большое значение, будет ли использован трёх или двух уровневый сумматор, не ужели эта 1 времени которая, будет сэкономлена при использовании двууровневого сумматора, а не трёх, так важна?! Ведь появляются всё новые и новые способы обработки информации, а мы всё сумматоры и сумматоры...
На основе СОК в советские времена была построена СОК-ЭВМ (СОК-компьютер), которая для задач некоторых типов показала хорошие результаты, но широкого распространения эти СОК-ЭВМ не получили.92.243.166.4 22:33, 29 октября 2008 (UTC)
Нужно добавить ссылки на 5Э53 и проект "Алмаз", чтобы было понятнее: http://www.pcweek.ru/themes/detail.php?ID=69856 http://www.pcweek.ru/themes/detail.php?ID=69914 http://www.electronics.ru/issue/2004/2/18
Не хватает
Надо бы дописать про перевод дробных чисел.
Не хватает нормального определения. 94.137.50.254 08:06, 30 мая 2011 (UTC)
Если уж добавлять, то про нецелые основания.
Дробные числа переводятся по тому же алгоритму, что и целые. Например, "0,25" в десятичной системе -- это два в минус второй степени, то есть, в соответствии с правилами записи в двоичной позиционной системе, "0,01". Нетрудно видеть, что полученное число при умножении на десятичную четвёрку (которая в двоичном виде выглядит как "100") даёт обычную единицу. Этого и следовало ожидать. Труднее будет (исключительно психологически!) при переводе тех дробей, которые в десятичной системе привычно коротки, а в других -- дают бесконечные "хвосты". Зато одна третья в троичной системе выглядит просто замечательно (догадайтесь, как).
А вот нецелые основания -- это поинтереснее. А ещё интереснее, если основание иррациональное... Но я такие вещи видел только однажды и то краем глаза.
Нужен раздел про традиционные системы счисления разных народов
--Nxx 16:16, 23 марта 2006 (UTC)
Русская Словесная Система Счисления (РССС), в определённых пределах, является непозиционной системой счисления. Например, десятичное число 12310 в русской словесной системе счисления "сто двадцать три" позволяет произвольно менять числа местами, т. е., если эти три числа поменять местами в любом порядке, то число не изменится: "сто+двадцать+три=123", "двадцать+три+сто=123", ..., "три+сто+двадцать=123". В такой системе в сумматор можно "засыпать" слагаемые, записанные в любом порядке, сумма от этого не изменяется. Это свойство используется в документах, в которых требуется указывать "число прописью". 92.243.166.4 00:20, 30 октября 2008 (UTC)92.243.182.100 16:23, 23 апреля 2009 (UTC) Андрей Куликов 16:24, 2 ноября 2009 (UTC)
Отрицательное основание
Также ни слова про системы счисления с отрицательным основанием. В таких системах счисления не нужен знак для обозначения отрицательных чисел.
Добавил статью по этому поводу, см. Нега-позиционная система счисления. Пельмень 10:11, 3 мая 2008 (UTC)
Если в определении позиционных систем счисления снять с основания системы b ограничение в виде модуля, то такое определение включает в себя и положительные позиционные системы счисления и отрицательные позиционные (нега-позиционные) системы счисления. Пельмень - молодец!92.243.166.4 23:55, 29 октября 2008 (UTC)92.243.166.4 01:31, 30 октября 2008 (UTC)
Единичная система счисления
Может стоить написать про единичную систему счисления? Ведь это тоже способ записи чисел. В англоязычной статье, кстати, про нее есть информация.
Всё украдено до нас. Унарная система счисления. ManN 11:02, 19 июля 2007 (UTC)В той статье указано, что "Дробные числа записываются в виде дроби из двух целых чисел", но нет упоминания, что любое число, записанное в виде десятичной дроби (в одну строку с разделительным знаком- точкой или запятой) можно обозначить и используя только одну цифру, например: 111,1 = 3,1 (инфолиократ) 178.122.63.246 12:08, 1 мая 2011 (UTC)
Если в определении позиционных систем счисления расширить область возможных значений оснований с b>1 до b=>1, то такое определение включает в себя и единичную систему счисления.92.243.166.4 00:33, 30 октября 2008 (UTC)
Задача какое минимальное основание должна иметь система счисления, если в ней могут быть записанны числа:10,21,201,1201?объяснить ответ 85.174.112.146 12:13, 25 октября 2008 (UTC)
Если эти числа записаны в десятичной системе счисления, то, казалось бы, что b=10, но в условии сказано "минимальное основание", подходит и b=1/2 и b=1/3 и b=1/4 и ... и b=1/n и b=1/(n+1) ... , так как этот ряд возможных оснований бесконечен, то для любого из возможных оснований всегда найдётся ещё меньшее основание, т. е. в такой постановке задача решения не имеет.
Если эти числа записаны в троичной системе счисления, то, казалось бы, что b=3, но в условии сказано "минимальное основание", подходит и b=1/2 и b=1/3 и b=1/4 ... и b=1/n и b=1/(n+1) ... , так как этот ряд возможных оснований бесконечен, то для любого из возможных оснований всегда найдётся ещё меньшее основание, т. е. и в такой постановке задача решения не имеет.92.243.166.4 01:24, 30 октября 2008 (UTC)
Нецелочисленные системы счисления
Скажите, где подробно можно почитать про системы счисления с нецелым основанием? И про системы с иррациональным основанием.
Простейшим примером систем счисления c нецелочисленным иррациональным основанием являются натуральные логарифмы.92.243.166.4 00:02, 30 октября 2008 (UTC) Так как в определении позиционных систем счисления нет ограничения на нецелые основания, то в это определение входят все положительные позиционные системы счисления с основаниями большими единицы, в том числе и нецелочисленные, кроме отрицательных оснований.92.243.166.4 01:36, 30 октября 2008 (UTC)
Если считать половинами, третями, четвертями и т. д., то это будут: половинная позиционная система счисления, третичная позиционная система счисления, четвертичная позиционная система счисления и т. д.. Если в определении позиционных систем счисления снять ограничение и разрешить значения оснований из области действительных положительных чисел меньших 1, то такое определение включает в себя все эти системы.
Очевидно, что в определении позиционных систем счисления нужно снять ограничения с области возможных значений оснований систем счисления и расширить область их определения до всех действительных чисел, такое определение включает в себя нега-позиционные системы счисления (с отрицательными основаниями.92.243.166.4 01:28, 30 октября 2008 (UTC)
Очевидно также, что теоретически основаниями систем счисления могут быть и комплексные числа.92.243.166.4 00:52, 30 октября 2008 (UTC)
Во-первых, описанию таких систем счисления место в статье позиционная система счисления, так как в статье система счисления дается лишь краткое описание основного общепринятого понятия позиционных систем счисления (среди прочих систем счисления). Во-вторых, системы счисления с нецелочисленными основаниями являются довольно специальным обобщением общепринятого понятия, поэтому в статье позиционная система счисления оно должно быть описано в разделе обобщений. Maxal 02:46, 21 мая 2009 (UTC)Инструменты перевода систем
Указано как из 1 системы перевести в другую, но не указано чем можно. Fractaler 11:00, 15 октября 2009 (UTC)
Ручкой и бумагой можно. Либо вообще только мозгом... infovarius 17:47, 15 октября 2009 (UTC) Люди сказывали, что есть некие демоны, так они без ручек и бумаг именно что вообще только своим мозгом. Вроде кулькуляторами звать. Fractaler 13:12, 17 октября 2009 (UTC) В уме переводить довольно просто, например любое двуразрядное число любой позиционной системы я могу перевести в десятичную (с другими надо упражняться, пока с 16-ричной получается немного). Advisor ГоворитьОценить 17:47, 31 октября 2009 (UTC)Позиционные системы счисления
Повторю сказанное в Обсуждение:Позиционная система счисления:
Согласно ВП:ПУ, изложение фактов в статье должно идти от простого к сложному, в порядке важности и известности. Под позиционными системами счисления обычно понимаются b-ричные системы счисления, где b — натуральное число. … Системы счисления с отрицательными основаниями, нецелыми основаниями, несколькими основаниями и т.д. являются обобщениями общепринятого понятия и изучаются лишь в специальной литературе. Поэтому их упоминание в данной статье возможно лишь в разделе обобщений, подробное же описание должно идти в отдельных тематических статьях. Не нужно пытаться определять обычные позиционные системы счисления с точки зрения этих специальных обобщений, навешивая ярлыки такие как одинарная, показательная, целочисленная, что она определяется двумя равными основаниями и т.д. Таким подробностям самое место в специальных тематических статьях (типа комбинированная система счисления), где они ни у кого не вызовут нареканий.В дополнение замечу, что статья Система счисления является обзорной, и в ней тем более неуместна детальная информация об очень специальных обобщениях. Maxal 17:08, 31 октября 2009 (UTC) Новые тонкости прошу обсуждать в "Обсуждение:Новая система счисления" 178.122.105.94 06:54, 17 декабря 2011 (UTC).
- Коллеги, вы если начнете воевать, а не совместно редактировать, дайте знать, ок?--Victoria 17:19, 31 октября 2009 (UTC)
изложение фактов в статье должно идти от простого к сложному, но диалога с Андреем Куликовым пока как-то не получается - имею ввиду удаление моего кодирования 1 цифрой любых чисел в одну строку, как записываются т.н. десятичные дроби. В связи с вышеизложенным, прошу рассмотреть, является ли заслуживающей внимания 100-ричная система счисления. Внимание! Данная ссылка устаревшая, на нее можно попасть через новый квантофорум http://quantrinas.myff.ru/viewtopic.php?id=1092#p151671 93.84.85.43 18:18, 23 апреля 2012 (UTC). Новая, работающая ссылка: http://quantoforum.ru/mathematics/753-novaya-sistema-schisleniya-0-100-1000-10000-ili-i-aleforichnaya-perspek 178.120.145.81 05:45, 3 июля 2014 (UTC) (не говоря уже о 1000 ричной и 10000-ричной, миллионоричной, в которой, проще всего использовать для визуального различия вместо одной цифры три "сторичных" с верхним и нижним индексом ...), ведь число (разрядов) знаков в больших числах уменьшается соответственно в 2, 3 или 4 раза. Для нежелающих глянуть на Квантофоруме тему, приведу такой например набор латинских букв= соответствующих цифр c учетом начертания (
полужирныйкурсивподчеркнутыйзачеркнутый
даже более простые (не тройные, а двойные их комбинации), не говоря уже о цвете, позволяют получить отличие в записях одного и того же символа.
): a..z 1..25 a..z 25..50 A..Z 51..75 A..Y 76..99, а последняя цифра ..Z может обозначать не 100, а 00 (именно двойной ноль, при переводе в 10ричную систему счисления или наоборот) Предвижу обычные возражения, как было c Обратный факториал мол это тривиально (хотя далеко не все так считают, например на uforum.uz и на Квантофорум Матрица Математика есть одноименная тема) З павагай, инфолиократ178.122.63.246 13:01, 1 мая 2011 (UTC) 178.122.163.31 14:50, 6 июня 2011 (UTC)
Неточности в "Древнеегипетская система счисления"
В пункте 4.1 статьи "Система счисления" на мой взгляд допущена неточность. Цитирую: "Для обозначения чисел 0, 1, 10, 102, 103, 104, 105, 106, 107 использовались специальные цифры." Во всех источниках, которые я читал по этой системе не указан символ, которым древние египтяне обозначали символ 0. Так же упоминание о наличии этого символа присутствует только в данной статье. Если можно, укажите ссылку на изображение этой цифры в древнеегипетской записи, или, если таковой нет, исправьте пожалуйста статью. Заранее спасибо 93.73.34.35 17:43, 7 февраля 2010 (UTC)Aleksss
Четверичная и пятеричная
Наиболее употребляемыми в настоящее время позиционными системами являются: ... 4 — четверичная; 5 — пятеричная;Это где они на практике в настоящее время широко употребляются? --Insolor 20:42, 13 июля 2011 (UTC)
Отчёт бота WebCite Archiver
Бот WebCite Archiver просмотрел текст статьи и внёс в неё следующие изменения. 1 шаблонов {{citeweb}} были дополнены ссылками на только что созданную архивную копию материала. Оставшиеся ссылки были пропущены по различным причинам. Далее приведена детальная информация.
Детальная информацияСледующие ссылки были пропущены, так как они указывают на сайты, архивирование которых службой WebCite имеет технические сложности:
- http://books.google.com/books?id=TmbajGgliYYC&printsec=frontcover&hl=ru&source=gbs_v2_summary_r&cad=0#v=onepage&q=&f=false
Следующие ссылки были успешно архивированы:
Ссылка Ссылка на архивную копию| http://news.bbc.co.uk/2/hi/americas/4143968.stm | http://www.webcitation.org/611umbKKZ |
Спасибо за внимание! WebCite Archiver 17:06, 18 августа 2011 (UTC)
100-ричная система счисления (1000 и 10000 и др.) участник: инфолиократ
http://quantoforum.ru/category-58/753-novaya-sistema-schisleniya-0-100-1000-10000-ili-i-aleforichnaya-perspek Для нежелающих пройти по ссылке, приведенной выше. В качестве цифр новой системы счисления используются только латинские буквы, которых ровно 25. 178.122.111.238 10:07, 5 мая 2013 (UTC) Предложена, в соответствии со статьей Системы наименования чисел в вики МАТ=МАТИКА удобная легкозапоминающаяся оригинальная система названий чисел. См. основную статью: Именные названия степеней тысячи 178.122.99.61 20:18, 12 марта 2014 (UTC) Очевидно, что перевод чисел из одной системы счисления в другую сводится к простой записи 100 чисел цифр=латинских букв двухзначным числом из 10 цифр и наоборот. Естественно, что в отличие от двоичной и шестнадцатиричной системы счисления количество знакомест (цифр) для записи числа уменьшается не в четыре раза, а только в два. С учетом общепринятых навыков применения верхних и нижних индексов каждый желающий может сгененрировать 1 000 000 (миллионоричную систему счисления), тогда легкозапоминающаяся оригинальная система названий чисел позволит арабскими цифрами обозначать число миллионов миллионов, что в свою очередь позволит одной арабской цифрой одной латинской буквой с такими же верхними и нижними индексами записывать круглые числа с шестьюдесятью нулями. Хотя это и не гугол. но для практических целей всего лишь четырех знакомест будет достаточно. З павагай да сусветнатуральнага (всемирнонатуральное число) 178.120.37.78 03:28, 10 января 2016 (UTC) Мiкола iнфолiякрат участник: инфолиократ 178.122.175.34 07:35, 5 апреля 2014 (UTC)
Никаких "новых" систем счисления здесь быть не должно. Википедия новые идеи не продвигает. --Bopsulai 06:32, 10 января 2016 (UTC)Перестановки
Обсуждаемая правка: [1].@Admarkov: почему (5,3,1,2,4) неправильно? Если посчитать число инверсий, получится:
- число элементов меньших 5, но стоящих правее 5, равно 4;
- число элементов меньших 4, но стоящих правее 4, равно 0;
- число элементов меньших 3, но стоящих правее 3, равно 2;
- число элементов меньших 2, но стоящих правее 2, равно 0.
Так что получается (4,0,2,0), как и требовалось. — Алексей Копылов 19:40, 23 июня 2017 (UTC)
@Alexei Kopylov: Правильно считать инверсии так:
Например для (5,3,1,2,4)
- число элементов меньших 5, но стоящих правее 5, равно 4;
- число элементов меньших 3, но стоящих правее 3, равно 2;
- число элементов меньших 1, но стоящих правее 1, равно 0;
- число элементов меньших 2, но стоящих правее 2, равно 0.
Получается (4,2,0,0)
Я написал программу на с++, которая перебирает перестановки в лексикографическом порядке встроенной функцией next_permutation(). Действительно, сотая перестановка (при нумерации с 0) - это (5,1,4,2,3). Своим алгоритмом, описанным выше, я составил вектор инверсий для вашей перестановки (5,3,1,2,4), получилось (4,2,0,0). Переведя это число из факториальной системы в десятичную, я получил номер 108. И действительно, в качестве 108-ой перестановки (при нумерации с 0) программа (напоминаю, что алгоритм не мой, а встроенный в язык с++) вывела (5,3,1,2,4). Кроме того, те же ответы дал мне студент математико-механического факультета СПбГУ. Именно эта трактовка была дана нам на лекции и использована на практике. Исходя из всего этого у меня почти не осталось сомнений в том, что моя трактовка соответствия между числами в факториальной системе и перестановками верна, а Ваша нет.
Извиняюсь, если что-то делаю не так, я пока не умею правильно работать на Википедии. -- Admarkov 20:49, 23 июня 2017 (UTC)
- Если перебирать перестановки в лексикографическом порядке, то получится действительно, ваша перестановка. Но, если считать перестановки, как написано в тексте, то получится (5,3,1,2,4). Конечно можно считать инверсии и по вашему способу, но тогда в тексте должен быть описан этот способ, а то сейчас получается письмо дяди Фёдора. — Алексей Копылов 22:22, 23 июня 2017 (UTC)
ru.wikipedia.org
Что такое система счисления? плиз помогите...
Максим ю. Волков
Системы счисления
Для начала проведём границу между числом и цифрой. Число — это некоторая абстрактная сущность для описания количества (определение из Википедии) . Цифры — это знаки, используемые для записи чисел. Цифры бывают разные, самыми распространёнными являются арабские цифры, представляемые известными нам знаками от нуля (0) до девяти (9); менее распространены римские цифры, мы их можем иногда встретить на циферблате часов или в обозначении века (XIX век) .
Итак запомним: число — это абстрактная мера количества, цифра — это знак для записи числа.
Существует множество способов записи чисел с помощью цифр. Эти способы грубо можно разделить на три части:
позиционные системы счисления;
смешанные системы счисления;
непозиционные системы счисления.
Позиционные системы счислений мы рассмотрим более подробно ниже. Расскажем вкратце о смешанных и непозиционных системах счислениях.
Денежные знаки - это пример смешанной системы счисления. Сейчас в России используются монеты и купюры следующих номиналов: 1 коп. , 5 коп. , 10 коп. , 50 коп. , 1 руб. , 2 руб. , 5 руб. , 10 руб. , 50 руб. , 100 руб. , 500 руб. , 1000 руб. и 5000 руб. Чтобы получить некоторую сумму в рублях, нам нужно использовать некоторое количество денежных знаков различного достоинства. Предположим, что мы покупаем пылесос, который стоит 6379 руб. Чтобы расплатиться, нам потребуется шесть купюр по тысяче рублей, три купюры по сто рублей, одна пятидесятирублёвая купюра, две десятки, одна пятирублёвая монета и две монеты по два рубля. Если мы запишем количество купюр или монет начиная с 1000 руб. и заканчивая одной копейкой, заменяя нулями пропущенные номиналы, то мы получим число, представленное в смешанной системе счисления; в нашем случае — 603121200000.
В непозиционных системах счисления величина числа не зависит от положения цифр в представлении чисел. Если бы мы перемешали цифры в числе 603121200000, то мы бы не смогли понять, сколько стоит пылесос; в непозиционной системе цифры числа можно перемешивать, при этом сумма не изменяется. Ярким примером непозиционной системы счисления является римская система.
Алексей бараев
Систе́ма счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.
Система счисления:
* даёт представления множества чисел (целых или вещественных)
* даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)
* отражает алгебраическую и арифметическую структуру чисел.
Системы счисления подразделяются на позиционные, непозиционные и смешанные.
Вшивамвпyдру шолптынаxу
метод записи чисел, представление чисел с помощью письменных знаков. наиболее известны
1 - единичная счёт на пальцах, зарубки, узелки «на память» и др. ;
2 - двоичная используетсяв дискретной математике, информатике, программировании;
3 - троичная;
4 - четверичная;
8 - восьмеричная;
10 - десятичная используется повсеместно;
12 - двенадцатеричная (счёт дюжинами) ;
16 - шестнадцатеричная используется в программировании, информатике, а также в шрифтах;
60 — шестидесятеричная единицы измерения времени, измерение углов и, в частности, координат, долготы и широты.
Читайте также
![Структурное и функциональное определения операционной системы Структурное и функциональное определения операционной системы]() Структурное и функциональное определения операционной системы
Структурное и функциональное определения операционной системы- Политическая система определение
- Определение информационной системы
![Система определение Система определение]() Система определение
Система определение![Поисковая система это определение Поисковая система это определение]() Поисковая система это определение
Поисковая система это определение![Определение группы крови по системе аво Определение группы крови по системе аво]() Определение группы крови по системе аво
Определение группы крови по системе аво![Система целей управления персоналом является основой определения Система целей управления персоналом является основой определения]() Система целей управления персоналом является основой определения
Система целей управления персоналом является основой определения![Экономическая система определение Экономическая система определение]() Экономическая система определение
Экономическая система определение![1 Структурное и функциональное определения операционной системы 1 Структурное и функциональное определения операционной системы]() 1 Структурное и функциональное определения операционной системы
1 Структурное и функциональное определения операционной системы![Нервная система определение Нервная система определение]() Нервная система определение
Нервная система определение![Электрический ток определение Электрический ток определение]() Электрический ток определение
Электрический ток определение![Автомобиль определение Автомобиль определение]() Автомобиль определение
Автомобиль определение
 Структурное и функциональное определения операционной системы
Структурное и функциональное определения операционной системы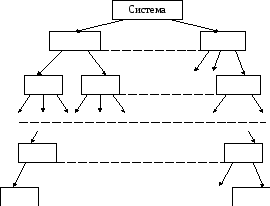 Система определение
Система определение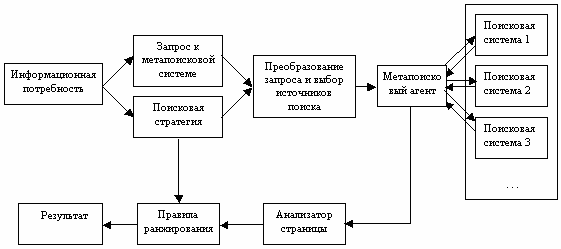 Поисковая система это определение
Поисковая система это определение Определение группы крови по системе аво
Определение группы крови по системе аво Система целей управления персоналом является основой определения
Система целей управления персоналом является основой определения Экономическая система определение
Экономическая система определение 1 Структурное и функциональное определения операционной системы
1 Структурное и функциональное определения операционной системы Нервная система определение
Нервная система определение Электрический ток определение
Электрический ток определение Автомобиль определение
Автомобиль определение