Теория графов: основные определения
Теория графов – раздел математики, используемый в информатике и программировании, экономике, логистике, химии.
Что такое граф
Часто для описания строения систем используют графические схемы. Элементы в них изображают кружками, точками, квадратами и т. п., а связи между элементами – линиями или стрелками. При этом ни то, как изображаются элементы, ни длина или форма линий не важны – имеет значение только, какие элементы соединены. Итак, граф – это пара вида (A, M), где A – конечное множество вершин, а M – множество ребер – линий, связывающих некоторые вершины.
Основные понятия теории графов
У ориентированного графа или орграфа (см. рисунок ниже) ребра ориентированы, называются дугами и изображаются стрелками. Дуга может быть обозначена упорядоченной парой вершин, которые она связывает, – начальной и конечной.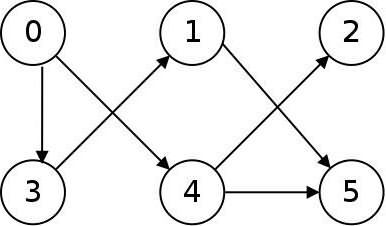
У неориентированного графа (см. рисунок ниже) ребра изображаются линиями без ориентации. Соответственно, пара вершин, которую связывает ребро, является неупорядоченной. Обе эти вершины есть концы ребра.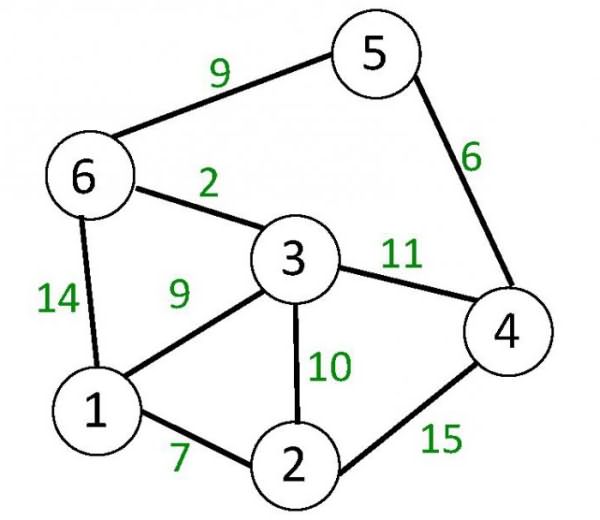
Если вершины a и b – концы ребра (или начало и конец дуги) графа, то говорят, что вершины a и b инцидентны этому ребру (дуге), также ребро (дуга) инцидентно вершинам a и b. Если вершины a и b – концы ребра, то они (a и b) называются смежными.
Чаще всего рассматривают графы, ребра которых имеют один тип – являются ориентированными или нет.
Если ребра имеет одинаковые начало и конец, то их называют кратными ребрами, а граф, в котором они присутствуют, называется мультиграфом.
Теория графов также использует понятие «петля» – ребро, выходящее и заходящее в одну и ту же вершину. Граф, в котором есть петли, называется псевдографом.
Чаще всего встречаются неориентированные графы, у которых нет кратных ребер и нет петель. Такие графы называются обыкновенными. Они не имеют кратных ребер, поэтому можно отождествить ребро и соответствующую пару вершин.
Каждая вершина орграфа характеризуется:
- Полустепенью исхода. Это количество дуг, выходящих из нее.
- Полустепенью захода. Это количество дуг, которые входят в данную вершину.
Сумма полустепеней захода орграфа, а также сумма полустепеней исхода равны общему количеству дуг графа.
У неориентированного графа каждая вершина характеризуется степенью вершины. Так называется количество ребер, которые инцидентны вершине. Общая сумма степеней вершин графа есть количество ребер, умноженное на два: каждое ребро будет давать вклад, который равен двум.
Вершина со степенью 0 называется изолированной.
Висячей вершиной является вершина со степенью 1.
Теория графов называет пустым графом такой, в котором нет ни одного ребра. Полный граф – это обыкновенный граф, в котором смежны любые 2 вершины.
Взвешенные графы – это графы, вершинам или ребрам (дугам) которых или и вершинам, и ребрам (дугам) сразу, приписываются некоторые числа. Они называются весами. На втором рисунке показан неориентированный граф, ребра которого взвешены.
Графы: изоморфизм
Понятие изоморфизма используется в математике. В частности, теория графов определяет его так: два графа U и V изоморфны, если в этих графах существует биекция между множествами их вершин: каждые 2 вершины в графе U соединены ребром в том и только том случае, если в графе V связаны ребром те же вершины (которые могут по-другому называться). На рисунке ниже показаны два изоморфных графа, в которых между вершинами, окрашенными в одинаковые цвета и в первом, и во втором графе, существует вышеописанная биекция.
Пути и циклы
Путем в неориентированном или ориентированном графе является последовательность ребер, где каждое следующее начинается в вершине, в которой заканчивается предыдущее. Простой путь – такой, в котором все вершины, исключая, может быть, начальную и конечную, и ребра различны. Циклом в орграфе называется путь, у которого совпадают начальная и конечная вершины и который включает не менее одного ребра. Циклом в неориентированном графе является путь, который содержит не менее трех различных ребер. На втором рисунке циклом является, например, путь (3, 1), (6, 3), (1, 6).
Теория графов в программировании используется для построения граф-схем алгоритмов.
syl.ru
Основные понятия и определения теории графов
При составлении структурных матриц удобно пользоваться графом схемы. Теория графов и их применение к анализу электрических схем достаточно подробно освещены в работах[26,.31]. Поэтому для основательного изучения этого вопроса рекомендуется читателям обратиться к этим работам. Здесь же приводятся в краткой форме некоторые концепции и свойства графов, дается обзор структурных матриц, их взаимосвязь, т.е. те понятия, которые могут потребоваться при описании алгоритмов машинного анализа схем.
Граф схемы G представляет собой множество ветвей V и вершинY. Каждому элементу схемы соответствует ветвь графа. Каждому узлу соединения элементов в схеме соответствует вершина графа. Граф схемы может быть направленным иненаправленным. В направленном графе каждая ветвь имеет стрелку в том направлении, в котором принимается положительное направление тока через эту ветвь. Эта стрелка указывает также положительное направление напряжения ветви - стрелка направлена от вывода с положительным потенциалом. На рис. 3.1 изображена схема (а), ее направленный (б) и ненаправленный граф (в).
Приведем ряд определений графа, которые потребуются в дальнейшем изложении. Подграфом графа называется подмножество ветвей графа ViÎ V. Вершина и ветвь инцидентны друг другу, если вершина есть конечная точка ветви. Последовательностью ветвей являются ветви графа или подграфа, которые упорядочены так, что каждая пара соседних ветвей vi, vi+1, являются инцидентными общей вершине. Например; а, в, f, k, c, в, е, d на рис. 3.1. Кратностьветви - число обходов ветви в последовательности. В предыдущем примере ветвь "в" является двукратной, а остальные ветви однократными. Однократная последовательность содержит только ветви с кратностью, равной единице (например, а, в, е, d, к). Замкнутая однократная последовательность - это последовательность, в которой первая и последняя ветви имеют общую вершину (например: с, d, е, j, к, f, в). В противном случае однократная последовательность является разомкнутой. Степень вершины есть число ветвей, инцидентных этой вершине. Путь есть подграф, ветви которого образуют разомкнутую однократную последовательность, степень вершин в котором не превышает 2. Контур есть подграф, ветви которого образуют замкнутую однократную последовательность, степень всех вершин в котором равна 2. Граф является связным если существует путь между двумя любыми вершинами. Если это условие не выполняется, то граф является не связным. На рис. 3.2. изображена схема и ее граф, состоящие из двух изолированных подграфов. Деревом Т связного графа G называется подграф, который содержит все вершины графа, но не содержит контуров. Количество деревьев может быть конечное множество. На рис. 3.1,г изображено одно из множества деревьев графа. Ветви, принадлежащие дереву Т, называются ветвями дерева. Ветви, не принадлежащие дереву Т, называются хордами (связями). Все хорды, соответствующие данному дереву Т, образуют подграф, называемый дополнением дерева ТC.
Можно показать, что для связного графа с n вершинами любое дерево имеет n - 1 ветвей. Если граф является несвязным и состоит из p изолированных подграфов, то дерево несвязного графа имеет n - р ветвей. Соответственно, количество хорд графа, имеющего общее количество ветвей q, равно q – n + p. Число r = n - р называется еще рангом графа. Число q – n + p называется связностью графа. Сечением называется такое множество ветвей графа G, удаление которых понижает ранг графа на единицу. Другими словами, сечение делит связной граф на два изолированных подграфа. Например, на рис.3.1,в ветви а, в, е, к образуют сечение, т.к. их удаление делит граф на два изолированных подграфа, а ранг графа станет равным 7 - 2 = 5. Приведем еще ряд определений теории графов, широко применяемые при анализе электрических схем. Граф G является неразделимым, если каждый подграф графа G имеет, по крайней мере, две вершины, общие с его дополнением. Все остальные графы разделимы. Примером разделимого графа является несвязный граф. Связной граф является разделимым, если он содержит, по крайней мере, один подграф, имеющий только одну вершину, общую с его дополнением. Например, граф, изображенный на рис. 3.3,а. Такая вершина называется вершиной сечения по которой связной граф разделяется на два несвязных подграфа. С неразделимостью графа тесно связано понятие циклической связности.Граф циклически связный, если его любые две вершины находятся в контуре.
Дуальные графы. Граф G2 дуален графу G1, если r1 = q2 a r2 = q1, т.е. ранг первого графа равен числу ветвей второго графа и наоборот. Графически дуальность графов можно пояснить таким образом, когда вершина одного графа, соответствует контуру другого графа (см. рис. 3.3,6). Дуальными графы могут быть только планарные. Граф G является планарным, если он может геометрически изображен на плоскости так, чтобы не было двух ветвей, имеющих общую точку, которая не являлась бы вершиной. На рис. 3.3,в изображен непланарный граф, который соответствует трехфазной мостовой схеме.
Приведенный здесь обзор основных понятий теории линейных графов имеет большое значение при анализе электрических цепей. Он позволяет читателю сформулировать наглядную геометрическую интерпретацию основных законов цепей: к контурам применим ЗНК, к сечениям применим ЗТК. На понятии дерева базируются большинство алгоритмов формирования систем линейно-независимых уравнений Кирхгофа. Каждому дереву Т графа G соответствует своя система линейно-независимых контуров и своя система линейно-независимых сечений. Или, как принято в литературе, система главных контуров и система главных сечений. Из определения дерева следует, что каждая хорда дополнения дерева ТС замыкает путь по ветвям дерева, который является главным контуром этой хорды по ветвям относительно выбранного дерева. Системе хорд соответствует система главных контуров. Положительное направление обхода контура совпадает с направлением хорды Количество главных контуров равно q – n + p.
Главное сечение образуется следующим образом: удаление любой ветви дерева делит дерево на две части, соответственно множества вершин на два подмножества. Главное сечение образуется этой ветвью дерева и хордами, вершины которых принадлежат разным подмножествам. Положительное направление сечения выбирается согласно направлению ветви дерева. Количество главных сечений равно n + p.
Графы позволяют получить геометрическую интерпретацию структуры электрических схем. При машинном анализе схем используется алгебраическое отображение структуры схем с помощью следующих структурных матриц: матрицы инциденции А, матрицы контуров В, матрицы сечений Q.
Матрица инциденций. Для направленного графа с n узлами и q ветвями матрицей инциденций является матрица размером n ´ q
Aa = [aij],
где aij = 1, если ветвь j инцидентна узлу i и стрелка направлена от узла i;
aij = -1, если ветвь j инцидентна узлу i и стрелка направлена к узлу i;
aij = 0, если ветвь j не инцидентна узлу i. Например, для графа рис.3.1,b:
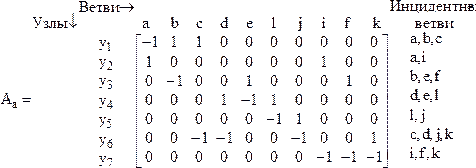
Т.к. каждая ветвь инцидентна двум вершинам, то каждый столбец структурной матрицы содержит только два ненулевых элемента (+1 и -1). Следовательно, сумма элементов в каждом столбце равна нулю. Сумма всех строк матрицы также равна нулю, т.е. строки структурной матрицы А линейно зависимы (одна из них равна сумме остальных строк с обратным знаком). Вычеркнув одну из строк матрицы А, получим сокращенную матрицу А размером (n-1)´q с линейно-независимыми строками. Эта матрица именуется далее редуцированной матрицей. инциденций. Матрицу А можно представить следующим образом:
A = [AT | AL] (3,8)
где субблок AT содержит столбцы, соответствующие ветвям дерева, а субблок АL - хордам. Из матричной алгебры известно, что для любой n´m матрицы максимальное количество линейно независимых строк и линейно независимых столбцов равны. Можно показать, что линейно независимые столбцы матрицы А соответствуют ветвям дерева, т.е. столбцы субблока линейно независимы. Рассмотрим субграф Т, состоящий из ветвей дерева. Для этого субграфа матрица АT является редуцированной матрицей инциденций размером (n-1)´(n-1). Т.к. субблок Т связан, то n-1 строк матрицы АT линейно независимы. Соответственно n-1 столбцов матрицы АT линейно независимы.
Матрица контуров. Для направленного графа G с q-ветвями и nk контурами матрицей контуров является матрица размером nk´q
Ba = [bij]
где bij = 1, если ветвь j входит в контур i и направление ветви совпадает с направлением обхода контура; bij = -1; если ветвь j входит в контур i и направление ветви противоположно направлению обхода контура; bij = 0, если ветвь j не входит в контур i. Количество контуров может быть сравнительно большим и матрица Ba содержит линейно независимые строки. Ниже будет показано, что ранг матрицы контуров связного графа равен q-n+1.
Из полной матрицы контуров можно выделить субматрицу с линейно независимыми строками, которая называется базовой матрицей контуров Вб. Извсех базовых матриц при анализе цепей широко используется матрица главных контуров В. При соответствующей расстановке столбцов и строк, матрица главных контуров может быть представлена в канонической форме
B = [BT | I] (3.9)
где: Вт субблок "контуры-ветви дерева" порядка (q-n+1)´(n-1); I - единичный субблок порядка (q-n+1)´(q-n+1). Из присутствия единичной матрицы следует, что строки матрицы В линейно независимы.
Если порядок следования столбцов матриц А и В одинаков, т.е. они взаимно соответствуют одним ветвям, то произведение строки матрицы А на транспонированную строку В равно нулю. Это исходит из определения контура как замкнутой однократной последовательности ветвей со степенью вершин равной 2. Если узел j принадлежит контуру i, то узлу j и контуру i инцидентны две общие ветви. Причем ориентация их относительно узла и контура противоположно. Тогда указанное выше произведение содержит два простых слагаемых (±1) с разным знаком. Отсюда следует ортогональность матриц А, В,
А × В' = 0 или В × А' = 0 (3.10)
где штрихом обозначены транспонированные матрицы.
Теперь можно подтвердить утверждение, что любая матрица Ва содержит
q – n + 1 линейно независимых строк. Пусть матрица Вa имеет количество строк больше q – n + 1, которую можно расчленить следующим образом
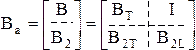 (3.11)
(3.11)
Тогда с учетом (3.8)
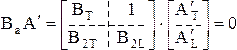 (3.12)
(3.12)
отсюда получим
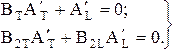 (3.13)
(3.13)
или
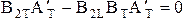 ; (3.14)
; (3.14)
т.к. 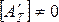 , то матрица А¢T имеет обратную. Умножим (3.14) на
, то матрица А¢T имеет обратную. Умножим (3.14) на 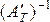 , получим:
, получим:
В2T = В2L×ВT,
следовательно
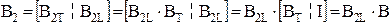 ,
,
т.е. строки матрицы В2 является линейной комбинацией строк В.
Для графа рис. 3.1,6 при выбранном дереве, состоящем из ветвей b, e, d, j, k, i, матрица главных контуров имеет вид:
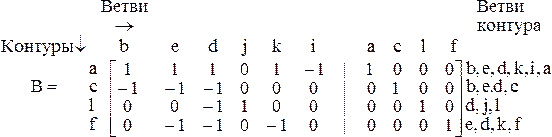
Здесь приняты обозначения главных контуров по обозначениям соответствующих хорд.
Матрица сечений. Для направленного графа G с q ветвями и nC сечениями матрицей сечении является матрица размером nC ´ q
Qa = [qij],
где qij = 1, если ветвь j входит в сечение i и направление ветви совпадает c прнятым положительным направлением сечения; qij = -1, если ветвь j входит в сечение i и направление ветви противоположно положительному направлению сечения; qij = 0, если ветвь j не входит в i-ое сечение. Ранг матрицы сечения равен n-1, т.е. из полной матрицы сечения Qa можно выделить субматрицу с n - 1 линейно независимыми строками, которая называется базовой матрицей сечения Qб. Из всех базовых матриц при анализе цепей широко используется матрица главных сечений. При соответствующей расстановке строк и столбцов, матрица главных сечений может быть представлена в канонической форме
Q = [I | QL] (3,15)
где I - единичный субблок размером (n-1)´(n-1); QL- субблок "сечения- ветви хорды" размером (n-1)´(q-n+1). Наличие единичного блока означает также то, что строки матрицы Q являются линейно независимыми.
Для графа рис. 3.1,6 при выбранном дереве, состоящем из ветвей b, e, d, j, k, i, матрица главных сечений имеет вид:
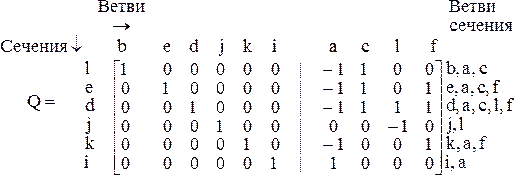
Обозначения главных сечений совпадают с обозначениями соответствующих ветвей дерева.
Легко показать, что любые контур и сечение имеют количество общих ветвей равным 2m [26]. Из них m ветвей имеют одинаковую ориентацию и в контуре и в сечении, т.е. их направление либо совпадает, либо противоположно с положительным направлением сечения и контура. Другие m ветвей имеют разную ориентацию в контуре и в сечении. Если, приэтом, порядок следования столбцов матриц В и Q одинаков, то произведение строки одной матрицы на транспонированную строку другой матрицы имеет m положительных и m отрицательных слагаемых, общая сумма которых равна нулю. Отсюда следует ортогональность матриц В и Q:
B × Q¢ = 0 или Q × B¢ = 0 (3.16)
где штрихом обозначена транспонированная матрица. Из (3.9, 3.15) следует:
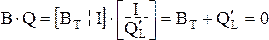
следовательно
BT = -Q¢L или QL = -B¢T (3.17)
Далее примем обозначение
T = BT = -QL (3.18)
Или

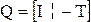
Покажем, что любая матрица Q содержит (n-1) линейно независимых строк. Представим Qa
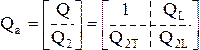
Тогда
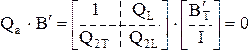 ,
,
отсюда
B¢T + QL = 0, Q2T × B¢T + Q2L = 0;
Или
Q2L = Q2T × QL
Тогда

т.е. строки матрицы Q2 являются линейной комбинацией строк Q.
В соответствии с первым законом Кирхгофа алгебраическая сумма токов ветвей, инцидентных данной вершине равна нулю. Пусть токи ветвей образуют вектор столбец i порядка q´1. Если порядок следования столбцов матрицы А и токов ветвей в векторе совпадают, т.е. взаимно соответствуют одним и тем же ветвям, то уравнение ЗТК в обобщенной форме имеет вид [26]:
A×i = 0 (3.19)
Применительно к сечениям первый закон Кирхгофа трактуется следующим образом: сумма токов сечения равна нулю. Обобщенная форма записи ЗТК имеет вид [26]:
Q×iv = 0 (3.20)
Второй закон Кирхгофа устанавливает, что алгебраическая сумма напряжений в каждом контуре схемы равна нулю. Пусть напряжения всех ветвей образуют вектор столбец u порядка q´1. Если порядок следования столбцов матрицы А и напряжений ветвей в векторе совпадают, т.е. взаимно соответствуют одним и тем же ветвям, то уравнение ЗНК в обобщенной форме имеет вид[26]:
B×u = 0 (3.21)
Т.к. сумма линейно независимых контуров и сечений равна q. Таким образом, ранг системы структурных уравнений (3.20, 3.21) равен q.
Множество ветвей дерева разбивается на два подмножества - ветви дерева и хорды (ветви дополнения). Соответственно этому вектор напряжений (токов) ветвей можно разбить на два подвектора - вектор напряжений (токов) ветвей дерева и вектор напряжений (токов) хорд:
u = (uD, uX)¢, i = (iD, iX)¢.
Тогда из (3.9, 3.15, 3.20, 3.21) следует:
uX = -BT×uD (3.22)
или
uX = Q¢L×uD = -T¢×uD (3.23)
iD = -QL×iX (3.24)
или
iD = B¢T×iX = T×iX (3.25)
Из (3.23 и 3.25) следует, что напряжение всех ветвей схемы можно выразить через напряжение ветвей дерева, а токи всех ветвей через токи хорд (или контурные токи).
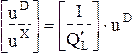 или u = Q¢×uD (3.26)
или u = Q¢×uD (3.26)
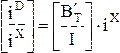 или i = B¢×iX (3.27)
или i = B¢×iX (3.27)
Уравнение (3.27) является частным случаем более общего контурного преобразования[2б], описываемого следующим выражением:
I = Ba×iK (3.28),
где Вa - некоторая матрица контуров; iK - вектор контурных токов.
Аналогично уравнение (3.26) является частным случаем более общего преобразования, называемого преобразованием сечений, и описывается формулой:
u = Qa×uS (3.29)
где Qa - некоторая матрица сечений; uS - вектор напряжений сечений.
Переменные iK и uS являются координатами, определяющими состояние схемы в q-мерном векторном пространстве.
Машинный анализ электрических схем заключается в выборе фундаментального дерева, в получении и преобразовании структурных матриц, формировании на их основе расчетной системы уравнений. В [12] описана реализация алгоритма получения структурных матриц В, Q с помощью преобразования матрицы инциденции А. Сам алгоритм получения матрицы А достаточно прост. Исходной информацией для него является таблица соответствия, которая представляет собой таблицу, содержащую обозначения ветвей и инцидентных им вершим, т.е. это, по сути, та же матрица инциденций в сжатой табличной форме. Развернуть ее в матрицу не представляет труда.
Учитывая, что столбцы субблока АT (3.8) являются линейно независимыми и они соответствуют ветвям дерева, то выделение ветвей дерева сводится к выделению в матрице А линейно независимых столбцов. Для поиска линейно независимых столбцов можно воспользоваться методам Гаусса[32]. Из (3.8, 3.9, 3.10) следует:
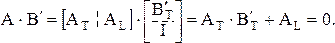
т.к. [AT] ¹ 0, то 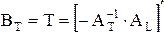 (3.30)
(3.30)
Дополняя матрицу Т единичными субблоками, можно получить матрицу главных контуров и матрицу главных сечений.
Итак, матричный метод получения В и Q состоит из следующих шагов:
1) формирование матрицы инциденции А из таблицы соответствия;
2) выделение линейно независимых столбцов в матрице А;
3) обращение субблока 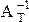 ;
;
4) выполнение матричного произведения 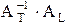 .
.
Хотя этот метод прост в реализации, однако он неэффективен. Это связано с необходимостью хранения промежуточных матриц А и 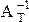 , которые являются разреженными (слабозаполненными ненулевыми элементами) и произведение разреженных матриц
, которые являются разреженными (слабозаполненными ненулевыми элементами) и произведение разреженных матриц 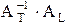 . Размер матрицы А и
. Размер матрицы А и 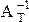 равен (n´q) и (n´n), коэффициент заполнения А равен
равен (n´q) и (n´n), коэффициент заполнения А равен 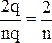
Итак, полная система уравнений электрической схемы включает уравнения ветвей (3.1) и структурные уравнения (3.6, 3.7). Эта система содержит 2q скалярных уравнения. В ряде случаев полную систему уравнений целесообразно преобразовать к системе порядка q, записанной относительно совместной сиcтемы координат - контурных токов и напряжений сечений. Расположим ветви графа в таком положении, чтобы сначало следовали i-ветви, а затем е-ветви. Представим уравнения ветвей в обобщенной операторной форме:
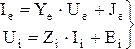 (3.31)
(3.31)
где Zi, Ye - соответственно матрицы обобщенных сопротивлений i-ветвей и проводимостей e-ветвей; J, Е - вектор значений задающих источников в операторной форме.
В соответствии с принятым расположением ветвей структурные уравнения (3.6, 3.7) можно записать в следующей форме:
 (3.32)
(3.32)
где Вi, Be - соответствующие субблоки матрицы контуров;
Qi, Qe - соответствующие субблоки матрицы сечений.
Подставив в (3.32) уравнения ветвей (3.31) и используя контурное преобразование (3.28) и преобразование сечения (3.29) получим результирующую систему уравнений в совместной системе координат (IК, US ):
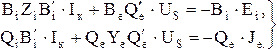 (3.33)
(3.33)
Или в матричной форме:
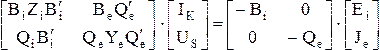 (3.34)
(3.34)
Система (3.34) содержит q уравнений
Определив по (3.34) переменные Iк, Us, напряжения и токи всех ветвей определяются по (3.28, 3.29).
Если графсхемы содержит только i-ветви, то уравнение (3.34) вырождается в результирующее уравнение относительно однородной системы координат (Iк) -уравнение контуров:
B×Z×B¢×Iк = -B×E (3.35)
Система (3.35) содержит n – q + 1 уравнение.
Если граф схемы содержит только е-ветви, то уравнение (3.34) вырождается в результирующее уравнение относительно однородной системы координат (US) - уравнение сечений
Q×Y×Q¢×Us =-Q×J (3.36)
В частном случае, когда ветвями дерева являются только е-ветви, а хордами i-ветви, субблоки Bi, Qe являются единичными (3.9, 3.15). Тогда система (3.34) примет вид:
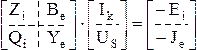 (3.37)
(3.37)
Использование той или иной формы записи результирующей системы уравнений и, соответственно, ее порядок зависят от выбранного метода анализа, распределения ветвей графа между е- и i-ветвями.
Особенностью больших схем является то, что соответствующие им структурные матрица являются разреженными, т.е. слабозаполненными ненулевыми элементами. Математические операции с такими матрицами являются неэффективными из-за действий с нулевыми элементами. Кроме большого времени вычислений может возникнуть трудность с размещением их в памяти машины. Например, уже для сравнительно небольшой схемы, изображенной на рис. 3.1,а коэффициент заполнения (отношение количества ненулевых элементов к общему количеству элементов) матрицы контуров В равен 17/40. Конечно, хранить в памяти машины полные матрицы контуров и сечений нет необходимости. Достаточно хранить только субблок Т размером (q-n+1)´(n-1). Избежать трудностей можно, если в памяти машины вместо (q-n+1)´(n-1) элементов этого субблока хранить только ненулевые элементы. Одной из форм такого хранения является представление матриц контуров и сечений структурными списками. Структурные списки используются двух видов. В первом случае элементами списков являются номера ветвей с соответствующим знаком. Во втором случае элементами списков являются адреса ненулевых элементов по номеру столбца (строки) матрицы с соответствующим знаком. Например, матрица главных контуров представлена контурными списками вида:
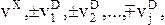
где vX - номер ветви хорды или номер строки матрица контуров; vD- номер ветви дерева или номер столбца матрицы контуров.
Аналогично может быть представленаматрица главныхсечений.Такое представление возможно только для целочисленных матриц, элементами которых являются простые числа 0, I, -I. При таком представлении структурных матриц умножение на них заменяется последовательным сложением тех элементов вектора сомножителя, которые соответствуют номеру ветви (столбца).
studopedia.ru
Основные определения теории графов
История и применение
Глава 3. Введение в теорию графов
Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждении о кенигсбергских мостах (1736 г.) Однако, она не находила применения в течение почти 100 лет. Интерес к теории возник благодаря исследованиям электрических сетей, моделей кристаллов и структур молекул. В 1847 г. Кирхгофом была разработана теория деревьев, которая послужила важным аналитическим средством для исследования электрических цепей. Законы Кирхгофа для напряжений и токов в цепи полностью определяются контурами и сечениями графа этой цепи и не зависят от природы используемых элементов. Поэтому тщательное изучение понятий контура, сечения и дерева графа дало толчок многим открытиям в теории цепей и, кроме того, внесло большой вклад в теорию графов.
Характерно то, что в терминах графов формулируются многие понятия и задачи прикладных областей: теории игр и программирования, теории передачи сообщений, транспортных сетей, электрических цепей, организационной структуры общества, а также биологии и психологии. В области вычислительной техники теория графов занимает особое место. Она предоставляет большие возможности для построения эффективных алгоритмов и анализа их сложности, дает готовые решения многим задачам вычислительной техники, например, для задачи оптимизации компиляторов. В то же время исследования в каждой из прикладных областей приводят к развитию самой теории графов.
Граф – математический объект, описываемый двумя множествами: G=( V, E ), где V – так называемое множество вершин, а E – множество дуг.
Элементами множества дуг являются упорядоченные пары вершин, т.е. E={ ( a, b): aÎV, bÎV }, т.о. множество Е является подмножеством декартова произведения V´V. Порядок вершин в парах может и не учитываться, тогда элементы множества Е называют ребрами, а сам граф – неориентированным графом, в противном случае – ориентированным или Орграфом. В некоторых случаях рассматриваются так называемые смешанные графы, в них множество Е состоит из элементов обоих видов: дуг и ребер.
Обозначим вершины v1, v2, v3, ¼, а ребра e1, e2, e3, ¼. Вершины vi и vj, определяющие ребро ek, называются концевыми вершинами ребра ek=(vi, vj), а в случае орграфа – началом и концом дуги ek соответственно. Говорят также, что ребро ek (дуга) инцидентно вершинам vi, vj или, что вершины vi, vj инцидентны ребру (дуге) ek. Такие вершины называют смежными. Ребра называют смежными в случае, когда они имеют общую концевую вершину. Например, ek=(vi, vj) и em=(vi, vl) – смежные ребра.
В множестве ребер графа допускается более, чем одно ребро с одинаковыми концевыми вершинами. Такие ребра называются параллельными или кратными. Например: ek=(vi, vj) и em=(vi, vj) – кратные ребра.
Если обе концевые вершины ребра совпадают, то такое ребро называется петлей. Например: ek=(vi, vi) – петля.
Граф без петель и параллельных ребер называется простым, в противном случае – мультиграфом.
Граф, не имеющий ребер, называется пустым, а не имеющий вершин (а значит и ребер) – нуль‑графом.
Простой граф, у которого любая пара вершин смежна, называется полным.
Количество вершин в графе называется порядком графа.
Степенью или валентностью вершины называется число инцидентных ей ребер. Будем обозначать степень вершины vi – deg(vi). Вершина нулевой степени называется изолированной. Вершина степени 1 называется висячей, а ребро, инцидентное ей, называется висячим ребром. Заметим, что петля добавляет двойку к степени вершины.
§ 3.3. Способы задания графов
Рассмотрим три способа задания графов: графический, аналитический и матричный.
1) Графический способ.
Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.
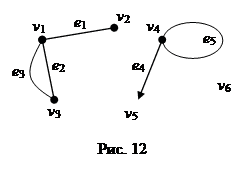 На рисунке 12 изображен смешанный граф с вершинами v1, v2,¼, v6, ребрами e1, e2, e3, e5 и дугой e4. Смежные вершины v1, v2, инциденты ребру e1. Вершины v1, v3, инциденты параллельным ребрам e2 и e3. Вершине v4 инциденты петля e5 и дуга e4, причем v4 является началом дуги e4, а v5 – концом этой дуги. Степень вершины v1 равна 3, вершины v2 – 1, вершины v3 – 2, вершины v4 – 3, вершины v5 – 1, вершины v6 – 0. Таким образом, вершины v2 и v5 – висячие, а вершина v6 – изолированная. В случае дуги e4 точнее было бы говорить о полустепенях исхода и захода вершин v4 и v5, а именно: полустепень исхода вершины v4 равна 3, вершины v5 – 0, полустепень захода вершины v4 равна 2, вершины v5 – 1.
На рисунке 12 изображен смешанный граф с вершинами v1, v2,¼, v6, ребрами e1, e2, e3, e5 и дугой e4. Смежные вершины v1, v2, инциденты ребру e1. Вершины v1, v3, инциденты параллельным ребрам e2 и e3. Вершине v4 инциденты петля e5 и дуга e4, причем v4 является началом дуги e4, а v5 – концом этой дуги. Степень вершины v1 равна 3, вершины v2 – 1, вершины v3 – 2, вершины v4 – 3, вершины v5 – 1, вершины v6 – 0. Таким образом, вершины v2 и v5 – висячие, а вершина v6 – изолированная. В случае дуги e4 точнее было бы говорить о полустепенях исхода и захода вершин v4 и v5, а именно: полустепень исхода вершины v4 равна 3, вершины v5 – 0, полустепень захода вершины v4 равна 2, вершины v5 – 1.
2) Аналитический способ.
Граф задают перечислением элементов множества вершин и множества ребер. Для графа, изображенного на рисунке 12, эти множества: V={v1, v2, v3, v4, v5, v6} и Е={e1, e2, e3, e4, e5}, где e1=(v1, v2), e2=(v1, v3), e3=(v1, v3), e4=(v4, v5), и e5=(v4, v4).
3) Матричный способ.
Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности.
а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом:

Таким образом, для графа на рисунке 12 матрица инциденций такова:
| e1 | e2 | e3 | e4 | e5 | |
| v1 | |||||
| v2 | |||||
| I= | v3 | ||||
| v4 | |||||
| v5 | -1 | ||||
| v6 |
По этой матрице легко судить о наличии в графе параллельных ребер (два одинаковых столбца), петли (одна единица в столбце), дуги (значения разных знаков в столбце), изолированной вершины (нулевая строка), висячих вершин (одно ненулевое значение в строке).
б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так:  . Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:
. Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:
| v1 | v2 | v3 | v4 | v5 | v6 | |
| v1 | ||||||
| v2 | ||||||
| S= | v3 | |||||
| v4 | ||||||
| v5 | ||||||
| v6 |
По виду этой матрицы также несложно судить о наличии в графе кратных ребер, дуг, петель, висячих и изолированных вершин.
Понятно, что любая квадратная матрица с целыми неотрицательными коэффициентами может быть интерпретирована как граф, а значит, изучение графов можно свести к изучению матриц такого типа. Вообще изучение графов можно расширить, рассматривая матрицы не только с целыми, но и с неотрицательными вещественными элементами. Такие матрицы, например, могут соответствовать графу, представляющему схему дорог, в котором расстояние между вершинами vi и vj равно длине соответствующей дороги. Подобные матрицы называют обычно матрицами весов.
Представление графов матрицами очень удобно при решении задач на компьютере.
studopedia.ru
4. Основы теории графов
4.1. Основные понятия и определения
Пусть дано множество V = {v1, v2, …, vn} и в V определено семейство U = {u1, u2, …, um} пар элементов uk= {vi, vj}, (k = 1, m) произвольной кратности и упорядочения. Пара {V, U} именуется: граф. Графы, как правило, обозначают прописными латинскими буквами, например, G, H. Принято также писать G(V, U) для того, чтобы определить некоторый конкретный граф G.
Элементы v1, v2, …,vn называются вершинами графа, а пары uk= {vi, vj}, (k = 1, m) — ребрами.
Определению графа можно дать следующую интерпретацию. Пусть имеем описание графа:
G(V,Е) = {{ v1, v2, …, v6}, { { v1, v3 }, v5, v1, {v3, v4},
v2, v3, {v3, v3 }}}.
Это описание можно отобразить графически, как показано на рисунке 4.1. На этом рисунке некоторые ребра отмечены стрелкой, а соответствующие им пары вершин в описании графа выделены угловыми скобками. Это связано с тем, что для некоторого произвольного ребра можно принимать или не принимать во внимание порядок расположения его концов.
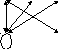
 v1 v4 v2
v1 v4 v2
V6
v3 v5
Рисунок 4.1
Если этот порядок не существенен, то ребро называется неориентированным, в противном случае ребро называется ориентированным. Ориентированные ребра называются также дугами.
Для ориентированного ребра определены понятия начальной и конечной вершины. Начальная вершина записывается в начале пары вершин, определяющих дугу,а конечная — в конце. Так на рисунке 4.1 ребра v5, v1 и v2, v3 являются дугами. Они представлены упорядоченными парами вершин и, в связи с этим, обозначены так же, как обозначаются упорядоченные множества.
Ребра {v1, v3}, {v3, v4} неориентированы. Для любого неориентированного ребра полагают, что {vi, vj} = {vj, vi} так же, как и в случае неупорядоченных множеств. Ребро {vi, vi} называется петлей. На рисунке 4.1 имеем петлю {v3, v3}. Петли обычно не ориентированы.
Граф, у которого все ребра неориентированы, называется неориентированным. Неориентированное ребро может быть эквивалентно паре ориентированных ребер, если это возможно по условию задачи.
Граф, у которого все ребра ориентированы, называется ориентированнымили орграфом.
На рисунке 4.1 приведен смешанный граф, т.е. содержащий как ориентированные, так и неориентированные ребра и петлю.
Многие теоремы и определения в теории графов могут быть отнесены как к ориентированным, так и к неориентированным графам. В таких случаях для обозначения ребер применяют круглые скобки, например, ребро {v3, v4} в графе рисунок 4.1 можно обозначать (v3, v4) либо (v4, v3), а ребро v5, v1 — соответственно как (v5, v1), указав при этом, что данное ребро представляет дугу. Принято также обозначение всех ребер круглыми скобками как в случае ориентированных графов, так неориентированных, если совершенно ясно о каком из типов этих графов идет речь в тексте.
Некоторые вершины графа G могут не войти в список пар. Такие вершины именуются изолированными. В рассмотренном примере это вершина v6. Граф, у которого все вершины изолированы, именуется нуль‑графом. Множество ребер такого графа пусто.
Антиподом нуль‑графа является полный граф. Ребрами полного графа являются всевозможные пары его вершин.
Как в случае ориентированного графа, так и в случае неориентированного — говорят, что ребро инцидентно паре определяющих его вершин.
Одной и той же паре вершин можно поставить в соответствие множество инцидентных ребер. Такие ребра называются кратными. Так на рисунке 4.2 представлена пара вершин (vi, vj), инцидентных трем различным ребрам u1, u2, u3. Одно из них направлено, а два — нет.
 u1
u1
vi u2 vj
u3
Рисунок 4.2
Граф называется плоским, если он может быть изображен на плоскости так, что все пересечения ребер есть его вершины. Так графы, представленные на рисунках 4.1 и 4.2 плоские. Примеры не плоских графов будут рассмотрены ниже в разделе 4.3.
Если граф G представлен конечным множеством ребер, то он называется конечным, независимо от числа вершин. В противном случае, граф называется бесконечным.
Граф H называется частью графа G или частичным графом H G, если множество его вершин V(H) содержится в множестве вершин V(G) графа G и все ребра H являются ребрами G. Частным, но важным типом частичных графов являются подграфы.
Пусть A — подмножество множества вершин V графа G. Подграф G(A) графа G есть такая часть графа, множеством вершин которого является A, а ребрами — все ребра из G, оба конца, которых лежат в A.
Для любой частиH графа определена дополнительная часть H (дополнение), состоящая из всех тех ребер, которые не принадлежат H и всех инцидентных им вершин.
StudFiles.ru
Читайте также
![Соответствие между понятиями и их определениями Соответствие между понятиями и их определениями]() Соответствие между понятиями и их определениями
Соответствие между понятиями и их определениями![Российский законодатель дает определения понятию информация Российский законодатель дает определения понятию информация]() Российский законодатель дает определения понятию информация
Российский законодатель дает определения понятию информация- Основные подходы к определению сущности права
![Определение понятия популяция человека в экологии Определение понятия популяция человека в экологии]() Определение понятия популяция человека в экологии
Определение понятия популяция человека в экологии- Дать определение понятию индустриализация
![Двигатель определение Двигатель определение]() Двигатель определение
Двигатель определение![Акт определение Акт определение]() Акт определение
Акт определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Машина определение Машина определение]() Машина определение
Машина определение![Определение ph воды Определение ph воды]() Определение ph воды
Определение ph воды![Обжалование определения Обжалование определения]() Обжалование определения
Обжалование определения![Определение цены деления шприца Определение цены деления шприца]() Определение цены деления шприца
Определение цены деления шприца
 Соответствие между понятиями и их определениями
Соответствие между понятиями и их определениями Российский законодатель дает определения понятию информация
Российский законодатель дает определения понятию информация Определение понятия популяция человека в экологии
Определение понятия популяция человека в экологии Двигатель определение
Двигатель определение Акт определение
Акт определение Болезнь определение
Болезнь определение Машина определение
Машина определение Определение ph воды
Определение ph воды Обжалование определения
Обжалование определения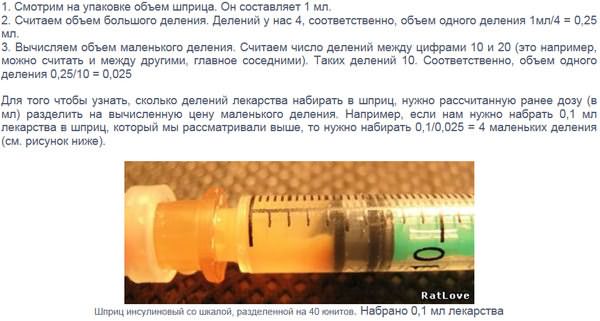 Определение цены деления шприца
Определение цены деления шприца