Способы определения положения центров тяжести
Центр параллельных сил и центр тяжести
Теорема Вариньона (общий случай)
Вопросы
Лекция 8
Покажем, что для любой системы сил, имеющей равнодействующую, справедлива следующая теорема Вариньона: момент равнодействующей относительно любого центра О равен сумме моментов всех сил системы относительно того же центра.
Доказательство.
 |
Пусть на тело действует некоторая система сил (А!, А@, А#, . . . ,А%), имеющая равнодействующую К , линия действия которой проходит через некоторую точку С. Приложим в этой точке силу -К, равную равнодействующей, но направленную в противоположную сторону.
Тогда система сил (А!, А@, А#, . . . ,А%,-К) будет находиться в равновесии и для нее будет выполняться условие (1.10):
Ьн=0, т.е. 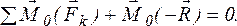
Учитывая, что 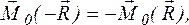 получаем
получаем 
 что и требовалось доказать.
что и требовалось доказать.
2. Центр параллельных сил и центр тяжести.
Вернемся к вопросу о сложении параллельных сил, рассмотренному в пятой лекции. Там было показано, что система двух параллельных и одинаково направленных сил А! и А@ имеют равнодействующую К=А!+А@, линия действия которой проходит через точку С, определяемую соотношением (1.5):
 |

Очевидно, что если повернуть силы А! и А@ на один и тот же угол а в одну и ту же сторону, то на этот же угол повернется и их равнодействующая, причем ее линия действия будет проходить через ту же точку С , так как в определяющее положение точки С выражение (1.5) входят только модули сил F1 и F2 .
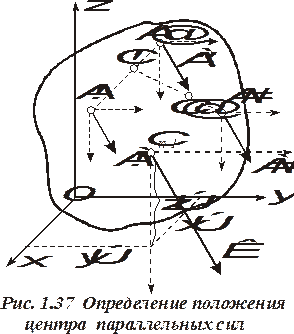 |
Рассмотрим теперь систему параллельных и одинаково направленных сил (А!, А@,А#,...,А%), приложенных в точках A1(x1,y1,z1), A2(x2,y2,z2),. . ., An(xn,yn,zn) твердого тела (рис.1.34). Эта система сил имеет равнодействующую К=СА$, а ее линия действия проходит через точку Сn-1, положение которой найдем, определяя последовательно положения точек С1, С2,...,Сn-1 с помощью выражений
 , записанных для k=1,2,3, . , n -1 (1.18)
, записанных для k=1,2,3, . , n -1 (1.18)
Так как в равенства (1.18) входят только модули рассматриваемых сил, положение точки Сn-1 относительно точек А1, А2, А3, . . . , Аn не изменится при любых одинаковых изменениях ориентации сил системы.
Определение: точка, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил на один и тот же угол в одну и ту же сторону, называется центром параллельных сил.
Найдем координаты этого центра в произвольной декартовой системе координат. Воспользуемся тем, что его положение не зависит от направления сил и направим все силы системы параллельно оси z (рис.1.34). Тогда по теореме Вариньона 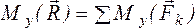 . Учитывая, что
. Учитывая, что 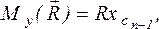
 , получаем
, получаем 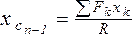 .
.
Применяя теорему Вариньона относительно оси x и относительно оси z (в последнем случае направив все силы параллельно оси y) получаем аналогичные формулы для 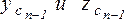 :
:
 . ( 1.19)
. ( 1.19)
Полученные формулы используем для определения положения центров тяжести тел, находящихся в однородном гравитационном поле земного тяготения. Действительно, силы тяжести отдельных частиц тела, размеры которого малы по сравнению с радиусом Земли, образуют систему параллельных сил, аналогичную рассмотренной выше. Назовем равнодействующую сил тяжести отдельных частиц тела весом этого тела и будем обозначать его буквой З. Центром тяжести будем называть центр параллельных сил тяжести 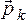 отдельных частиц тела и обозначать его буквой Р. В новых обозначениях формулы (1.19) перепишутся в виде:
отдельных частиц тела и обозначать его буквой Р. В новых обозначениях формулы (1.19) перепишутся в виде:
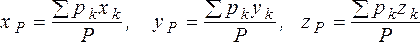 (1.20)
(1.20)
Для однородных тел вес pk отдельных частиц тела пропорционален объемам этих частиц : pk=g vk, а вес тела пропорционален объему тела P=g V (g - вес единицы объема). Подставляя данные выражения в (1.20), после сокращения на g , получаем формулы для определения центра тяжести объема:
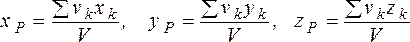 (1.21)
(1.21)
Для однородных плоских пластин и изделий из однородных линейных элементов (например, из однородной проволоки постоянного сечения), вводя вес единицы площади и вес единицы длины, аналогичных образом получаем формулы для определения центра тяжести площади и центра тяжести линии:
 (1.22)
(1.22)
где S - площадь всей пластины, sk - площади ее частей.
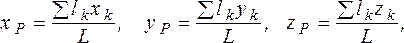 (1.23)
(1.23)
где L - длина всей линии, lk - длина ее частей.
3. Способы определения положения центров тяжести.
а) Способ симметрии. Если однородное тело имеет плоскость симметрии, ось симметрии или центр симметрии, то его центр тяжести находится соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.
б) Способ разбиения. Если тело можно разбить на конечное число частей, для которых положения центров тяжести известны, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам (1.21) - (1.23).
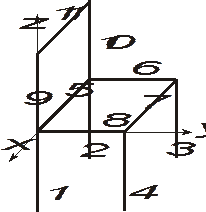 |
Пример 1. Найти координаты центра тяжести тела, имеющего вид стула, состоящего из стержней одинаковой длины и веса. Длина стержня равна l = 44 см.
Решение. Так как тело имеет плоскость симметрии и центр тяжести лежит в этой плоскости, то xc=-22 см. Остальные координаты определяем по формулам (1.23).
yc=[(l3+l4+l7)44+(l6+l8)]/(11·44)=16см.
zc=[-22(l1+l2+l3+l4)+l1144+(l9+l10)]/(11·44)=0.
в) Интегрирование. Если тело не удается разбить на несколько частей, положение центров тяжести которых известны, то тело разбивают на произвольные малые объемы Dvk иформулы (1.21) принимают вид:
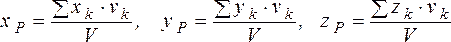 , (1.24)
, (1.24)
где xk, yk, zk - координаты некоторой точки, расположенной внутри объема Dvk
Переходя в формулах (1.24) к пределу при Dvk ® 0, получаем:
 (1.25)
(1.25)
Аналогичным образом, переходя в формулах (1.22) и (1.23) к пределу, получаем интегральные выражения для определения координат центров тяжести площадей и линий:
 (1.26)
(1.26)
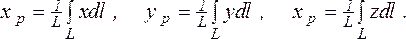 (1.27)
(1.27)
 |
Пример 2. Найдем положение центра тяжести дуги окружности АВ радиуса R c центральным углом 2а. В силу симметрии центр тяжести лежит на оси x. Для определения координаты y выделим на дуге элемент длиной dl = Rdф, положение которого определяется углом ф. Координата x этого элемента равна x = = Rcosф, длина АВ=L=R2а. тогда согласно (1.27):
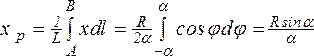 .
.
г) Способ дополнения (способ отрицательных масс). Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы. При этом центры тяжести тел без вырезов и центры тяжести самих вырезов должны быть известны.
 |
Пример 3. Дана однородная квадратная пластина ABDE со стороной а. Найти внутри квадрата такую точку С, чтобы она была центром тяжести площади, которая получится, если из квадрата вырезать равнобедренный треугольник ACB.
Решение: В силу симметрии xc=a/2. Для определения ус используем метод дополнения. Пусть S - площадь квадрата с вырезом, S1 , y1 - площадь квадрата без выреза и координата y его центра тяжести, S2 , y2 - площадь и координата y центра тяжести треугольника АСВ. Согласно (1.22): yc=å Skyk / S=(S1y1 - S2y2)/ S = (a2 a/2-0,5ayc yc/3)/(a2- 0,5ayc), 2yc2 - 6yc+3=0 , откуда ус= 0,61а (второй корень yc=2,4a не подходит по смыслу).
Лекция 9
Вопросы
studopedia.ru
§ 18. Силовое поле. Центр тяжести твердого тела
Область, в каждой точке которой на помещенную туда материальную частицу действует сила, зависящая от координат этой точки, называется силовым полем.
Например, на каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила тяжести. Эти силы образуют поле сил тяжести. Силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполняются эти два условия, называют однородным полем тяжести.
Равнодействующую сил тяжести ![]() ,
, ![]() ,…,
,…,![]() действующих на частицы тела, обозначим через
действующих на частицы тела, обозначим через ![]() (рис. 39). Модуль этой силы называется весом тела и определяется равенством
(рис. 39). Модуль этой силы называется весом тела и определяется равенством
![]() . (41)
. (41)
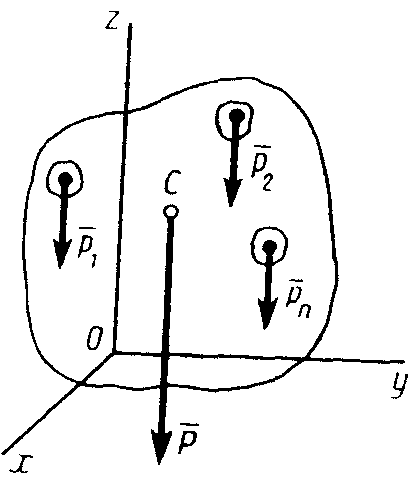
Рис. 39
При повороте тела силы ![]() остаются параллельными друг другу. Следовательно, равнодействующая
остаются параллельными друг другу. Следовательно, равнодействующая ![]() сил
сил ![]() будет при любых положениях тела проходить через одну и ту же точку С, являющуюся центром параллельных сил тяжести
будет при любых положениях тела проходить через одну и ту же точку С, являющуюся центром параллельных сил тяжести ![]() . Эта точка называется центром тяжести тела. Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы тела, при любом положении тела в пространстве.
. Эта точка называется центром тяжести тела. Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы тела, при любом положении тела в пространстве.
Координаты центра тяжести, как центра параллельных сил, определяются формулами (40); следовательно,
![]() ,
, ![]() ,
,![]() , (42)
, (42)
где xk,yk,zk – координаты точек приложения сил тяжести ![]() .
.
Отметим, что центр тяжести – это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).
§19. Координаты центров тяжести однородных тел
Для однородного тела вес pk любой его части и вес Р всего тела пропорциональны соответственно объемам vk этой части и V всего тела, т.е.
![]() ,
, ![]() ,
,
где – вес единицы объема.
Подставив эти значения Р и рk в формулы (42), получим
![]() ,
, ![]() ,
,![]() . (43)
. (43)
Как видно, положение центра тяжести однородного тела зависит только от его геометрической формы. Поэтому точку С, координаты которой определяются формулами (43), называют центром тяжести объема V.
Путем аналогичных рассуждений легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее
![]() ,
, ![]() , (44)
, (44)
где S – площадь пластины, sk – площади ее частей. Точку, координаты которой определяются формулами (44), называют центром тяжести площади S.
Точно также получаются формулы для координат центра тяжести линии:
![]() ,
, ![]() ,
, ![]() , (45)
, (45)
где L – длина линии, ℓk – длина ее частей.
Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.
§20. Способы определения координат центров тяжести тел
Исходя из полученных выше формул, можно указать способы определения координат центров тяжести тел.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии. Из свойств симметрии следует, что центр тяжести однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелепипеда, шара лежит в геометрическом центре (центре симметрии) этих тел.
2. Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести тела можно вычислить по формулам (42) – (45).
3. Дополнение. Этот способ применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
4. Интегрирование. Тело разбивают на произвольно малые объемы Δvk, для которых формулы (49) принимают вид
![]() ,
, ![]() ,
,![]() . (46)
. (46)
где xk,yk,zk – координаты некоторой точки, лежащей внутри объема Δvk. Затем в равенствах (46) переходят к пределу, устремляя все Δvkк нулю. Тогда суммы обращаются в интегралы и формулы (46) дают в пределе
![]() ,
,![]() ,
,![]() . (47)
. (47)
Аналогично для координат центров тяжести площадей и линий получаем:
![]() ,
, ![]() . (48)
. (48)
и
![]() ,
, ![]() ,
, ![]() . (49)
. (49)
5. Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации (самолет, тепловоз и т.п.) определяют экспериментально.
StudFiles.ru
/ шпоргалка / Статика / 20-22 билет
20. Координатыцентров тяжести однородных тел. Способы их определения.
Для однородного тела вес phлюбой его части пропорционален объему υhэтой части: pk=γυk, а вес Р всего тела пропорционален объему Vэтого тела, т. е. P=γV, где γ — вес единицы объема.
xc = 1/V Συk∙ xk;
yc = 1/V Συk∙ yk;
zc = 1/V Συk∙ zk.
Положение центра тяжести однородного тела зависит только от его геометрической формы, а от величины γ не зависит. По этой причине точку С, координаты которой определяются формулами, называют центром тяжести объема V.
Путем аналогичных рассуждений легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее.
xc = 1/S Σsk ∙ xk;
yc = 1/S Σsk ∙yk;
где S— площадь всей пластины; sk— площади ее частей.
Точку, координаты которой определяются формулами, называют центром тяжести площади S.
Точно так же получаются формулы для координат центра тяжести линии:
xc = 1/L Σlk∙ xk;
yc = 1/L Σlk∙ yk;
zc = 1/L Σlk∙ zk.
где L— длина всей линии; lk— длины ее частей.
Центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.
Центр тяжести треугольника лежит в точке пересечения его медиан.
CE = 1/3 BE.
Центр тяжести дуги. Окружности.
xc=2 Rsinα/α.
Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.
Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам. При этом число слагаемых в каждой из сумм будет равно числу частей, на которые разбито тело.
Дополнение. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
Интегрирование. Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают сначала на произвольные малые объемы Δυk, для которых формулы (60) принимают вид
xc = 1/V ΣΔυk∙ xk;
где xk, yk, zk— координаты некоторой точки, лежащей внутри объема Δυk. Затем в равенствах переходят к пределу, устремляя все Δυkк нулю, т. е. стягивая эти объемы в точки. Тогда стоящие в равенствах суммы обращаются в интегралы, распространенные на весь объем тела, и формулы дают в пределе:
xc = 1/V ![]() x dυ;yc = 1/V
x dυ;yc = 1/V ![]() y dυ;zc = 1/V
y dυ;zc = 1/V ![]() z dυ;
z dυ;
Аналогично для, координат центров тяжести площадей и линий получаем в пределе из формул:
xc = 1/S![]() x ds; yc = 1/S
x ds; yc = 1/S ![]() y dυ.
y dυ.
xc = 1/L ![]() x dl; yc = 1/L
x dl; yc = 1/L ![]() y dl; zc = 1/L
y dl; zc = 1/L ![]() z dl.
z dl.
Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации (самолет, паровоз и т. п.) можно определять экспериментально. Один из возможных экспериментальных методов (метод подвешивания) состоит в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, на которой подвешено тело, будет каждый раз давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела. Другим возможным способом экспериментального определения
центра тяжести является метод взвешивания.
21. Трение скольжения.
Трение – сопротивление, возникающее при перемещении одного тела по поверхности другого.
Трение скольжения – сила, возникающая при скольжении одного тела по поверхности другого.
Fпр = ƒo ∙ N,
где Fпр – предельная сила; ƒo – статистический коэффициент; N – сила нормального давления.
F = ƒ ∙ N,
где ƒ – динамический коэффициент.
Реакции шероховатых связей.
tgφo = ƒo
22. Трение качения.
Трение качения - сопротивление, возникающее при качении одного тела по поверхности другого.
Коэффициентом трения качения - линейная величина k, измеряется обычно в сантиметрах. Значение коэффициента kзависит от материала тел и определяется опытным путем.
Величина RN умноженная на k – момент трения качения. Растет до некоторой величины, с ростом вращающего момента F∙h
StudFiles.ru
Способы определения координат центра тяжести.
1. Симметрия.Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
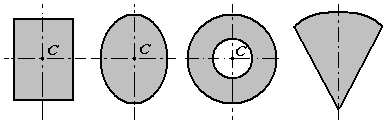
2. Разбиение.Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести и площадь известны.
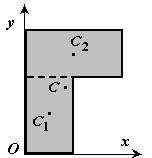

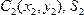

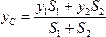
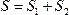
3. Дополнение.Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
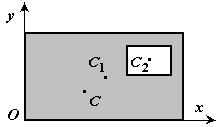

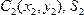
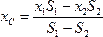
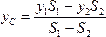

Центры тяжести некоторых однородных тел.
1)Центр тяжести дуги окружности.Рассмотрим дугу АВ радиуса R с центральным углом 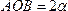 . В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 37).
. В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 37).
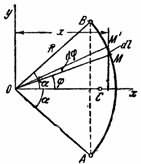
Рис.37
Найдем координату xC по формуле  . Для этого выделим на дуге АВ элемент ММ длиною
. Для этого выделим на дуге АВ элемент ММ длиною 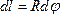 , положение которого определяется углом φ. Координата х элемента ММ’ будет
, положение которого определяется углом φ. Координата х элемента ММ’ будет 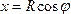 . Подставляя эти значения x и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
. Подставляя эти значения x и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
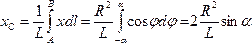
где L - длина дуги АВ, равная 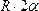 . Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном
. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном
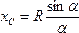
где угол α измеряется в радианах.
2) Центр тяжести площади треугольника. Разобьем площадь треугольника ABD (рис. 38) прямыми, параллельными AD, на узкие полоски; центры тяжести этих полосок будут лежать на медиане BE треугольника.
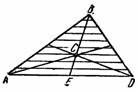
Рис.38
Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан.
При этом, как известно, 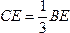
Пример 1.Определим центр тяжести однородного тела, изображённого на рис. 40.
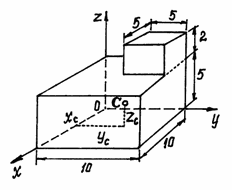
Рис.40
Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:
x1=5 см; y1=5 см; z1=2,5 см;
x2=2,5 см; y2=7,5 см; z2=6 см.
Объёмы их: V1=5·10·10=500 см3; V2=5·5·2=50 см3.
Поэтому координаты центра тяжести тела
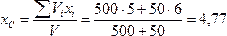 см;
см;
 см;
см;
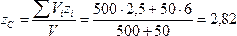 см;
см;
Пример 3.У квадратного листа 20x20 см вырезано квадратное отверстие 5x5 см (рис.42). Найдем центр тяжести листа.
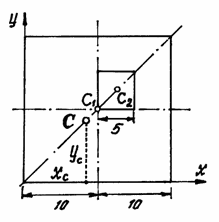
Рис.42
В этой задаче удобнее разделить тело на две части: большой квадрат и квадратное отверстие. Только площадь отверстия надо считать отрицательной. Тогда координаты центра тяжести листа с отверстием:
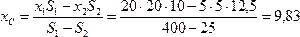 см
см
координата 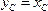 , так как тело имеет ось симметрии (диагональ).
, так как тело имеет ось симметрии (диагональ).
studopedia.ru
Читайте также
![Определение степени тяжести вреда здоровью при дтп Определение степени тяжести вреда здоровью при дтп]() Определение степени тяжести вреда здоровью при дтп
Определение степени тяжести вреда здоровью при дтп- Классификация факторов по способу определения
![Способы определения площади ожога Способы определения площади ожога]() Способы определения площади ожога
Способы определения площади ожога![Полярный способ определения координат Полярный способ определения координат]() Полярный способ определения координат
Полярный способ определения координат![Способы определения падежей Способы определения падежей]() Способы определения падежей
Способы определения падежей![Способы определения времени рефлекса Способы определения времени рефлекса]() Способы определения времени рефлекса
Способы определения времени рефлекса![Понятие функции способы задания функции область определения Понятие функции способы задания функции область определения]() Понятие функции способы задания функции область определения
Понятие функции способы задания функции область определения![Способы определения сторон горизонта Способы определения сторон горизонта]() Способы определения сторон горизонта
Способы определения сторон горизонта![Определение центра тяжести Определение центра тяжести]() Определение центра тяжести
Определение центра тяжести![Человек определение в обществознании Человек определение в обществознании]() Человек определение в обществознании
Человек определение в обществознании![Автомобиль определение Автомобиль определение]() Автомобиль определение
Автомобиль определение![3 Закон ньютона определение 3 Закон ньютона определение]() 3 Закон ньютона определение
3 Закон ньютона определение
 Определение степени тяжести вреда здоровью при дтп
Определение степени тяжести вреда здоровью при дтп Способы определения площади ожога
Способы определения площади ожога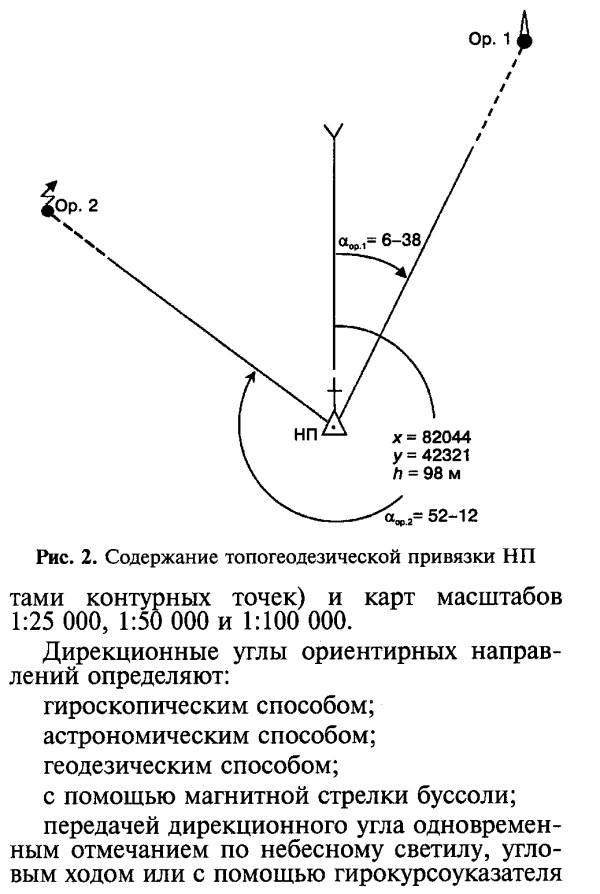 Полярный способ определения координат
Полярный способ определения координат Способы определения падежей
Способы определения падежей Способы определения времени рефлекса
Способы определения времени рефлекса Понятие функции способы задания функции область определения
Понятие функции способы задания функции область определения Способы определения сторон горизонта
Способы определения сторон горизонта Определение центра тяжести
Определение центра тяжести Человек определение в обществознании
Человек определение в обществознании Автомобиль определение
Автомобиль определение 3 Закон ньютона определение
3 Закон ньютона определение