Геометрическая формула определения вероятности события
Классическая формула определения вероятности события
Вероятность некоторого события А может быть найдена, как отношение количества исходов, благоприятствующих событию А к общему количеству исходов опыта, удовлетворяющих схеме случаев.
Р(А) = m/n, (1)
где n – общее количество исходов опыта, удовлетворяющих схеме случаев;
m – количество исходов, благоприятствующих событию А.
Схема случаев подразумевает три обязательных условия применения классической формулы:
1) исходы опыта должны быть несовместными;
2) исходы опыта должны образовывать полную группу;
3) исходы опыта должны быть равновозможными.
Пример 7
Определить вероятность того, что будет произведен выстрел при игре в русскую рулетку. Для ещё не игравших в эту азартную (но не виртуальную) игру сообщим правила. В восьми зарядный револьвер вставляется один патрон. Барабан раскручивается случайным образом, и игроки по очереди нажимают на курок, приставив дуло к своему виску.
Решение. Вероятность того, что револьвер выстрелит с первой попытки Р(А)=1/8, так как всего возможно восемь исходов (восемь положений барабана), все восемь исходов равновозможны и несовместны.
Пример 8
Монета подбрасывается два раза. Найти вероятность того, что хотя бы один раз монета упадет гербом вверх.
Этот пример часто называют «примером с ошибкой Д’Аламбера», так как при его решении известный французский математик и философ (1717 – 1783) допускал важную методологическую ошибку.
Д’Аламбер считал, что возможны три несовместных исхода, образующих полную группу:
– монета дважды упала цифрой вверх;
– монета дважды упала гербом вверх;
– по одному разу наблюдались герб и цифра.
Из этих исходов поставленному вопросу благоприятствуют последние два исхода. В результате искомая вероятность «по Д’Аламберу» равна 2/3. Однако это решение ошибочно.
Причина ошибки заключается в том, что перечисленные выше исходы не являются равновозможными. Первые два исхода можно получить единственным способом: обязательно цифра при первом подбрасывании и обязательно цифра при втором подбрасывании (для первого исхода), обязательно герб при первом подбрасывании и обязательно герб при втором подбрасывании (для второго исхода). Третий исход Д’Аламбера можно получить двумя путями: сначала цифра – потом герб или сначала герб – потом цифра, т.е. он будет наблюдаться в два раза чаще, чем любой из предыдущих исходов.
Решение. Равновозможных исходов, соответствующих «схеме случаев», необходимо рассматривать четыре: ЦЦ, ГГ, ГЦ, ЦГ (здесь использованы следующие обозначения: «Г» - монета упала гербом вверх, «Ц» - монета упала вверх цифрой).
Интересующему событию (монета хотя бы один раз упала гербом вверх) благоприятствуют три последних исхода. Таким образом, искомая вероятность равна 3/4.
Классическую формулу определения вероятности нельзя применять, если:
1) не выполняется схема случаев;
2) числитель и знаменатель дроби стремятся к бесконечности.
Рассмотрим пример.
Пример 9
На линии электропередачи длиной 80 км произошел обрыв провода (рис. 15). Считая, что возможность обрыва в любом месте линии одинакова, определить вероятность того, что обрыв произошел на участке СВ длиной 20 км.
АВ = L = 80км, СВ = l = 20км.
 Решение:
Решение:
Количество возможных исходов опыта (мест обрыва) на участке СВ бесконечно велико, так как оно равно числу точек, которое можно поставить на этом участке. Также бесконечным является количество возможных мест обрыва на всей линии АВ. Поэтому классическую формулу вычисления вероятности использовать нельзя (её применение даёт в результате неопределенность). Несложно предположить, что если бы участок СВ составлял половину длины всей ЛЭП, то вероятность обрыва на этом участке составляла бы 0,5, причем независимо от того, где расположен этот участок (в начале ЛЭП, в её конце или в середине) и является ли он цельным или разрывным. Для участка, составляющего 25% длины ЛЭП, ответ равен 0,25 и т.д. Таким образом, вероятность Р(С) обрыва на участке СВ может быть найдена как отношение длины этого участка к длине всей линии:
Р(С) = l/L = 20/80 = 1/4 = 0,25.
В наиболее общем виде формула имеет вид:
Р(А) = mes d/mes D. (2)
Иначе говоря, геометрическая вероятность определяется как отношение меры mes d области d, благоприятствующей событию А, к мереmes D всей области D.
Понятие мера (mes) применяется в теории множеств и является обобщением понятий длина отрезка, площадь плоской фигуры и объём тела на множества более общей природы. Для задач, рассматриваемых в рамках настоящего курса, мерой области являются:
1) для линий – их длина: Р(А) = l/L;
2) для плоских фигур – площадь: Р(А) = s/S;
3) для тел – объем: Р(А) = v/V,
где малыми буквами обозначены меры областей, благоприятствующих рассматриваемому событию, а большими – меры всей области.
Пример 10
 Произошел перерыв электроснабжения цеха в течение периода наблюдения, равного одним суткам. Считая, что возможность отключения электроэнергии в любое время суток одинакова, определить вероятность того, что момент отключения пришелся на одну из рабочих смен общей длительностью 16 ч.
Произошел перерыв электроснабжения цеха в течение периода наблюдения, равного одним суткам. Считая, что возможность отключения электроэнергии в любое время суток одинакова, определить вероятность того, что момент отключения пришелся на одну из рабочих смен общей длительностью 16 ч.
Решение: Условие задачи можно представить в виде линейной схемы (рис. 16), поэтому целесообразно воспользоваться геометрической формулой определения вероятности события. Обозначив искомую вероятность Р(А), получаем ответ:
Р(А) = l/L= ТР/Т = 16ч/24ч = 2/3.
 Этот пример показывает, что в геометрической формуле понятие «длина» не следует понимать буквально, в зависимости от условий задачи «длина» может измеряться не только в метрах, но и в других единицах.
Этот пример показывает, что в геометрической формуле понятие «длина» не следует понимать буквально, в зависимости от условий задачи «длина» может измеряться не только в метрах, но и в других единицах.
Пример 11
По диаграмме Венна (рис. 17) определить вероятность события А.
Решение: По геометрической формуле вычисления вероятностиР(А) = s/S
Ввиду того, что основу диаграммы составляет «единичный» квадрат (стороны равны единице), S=1.
Следовательно, Р(А) = s, т.е. на диаграмме Венна вероятности событий численно равны площадям фигур, обозначающих эти события.
Геометрическая формула неприменима, если нарушается условие равновозможности появления события в любой части рассматриваемой области (линии, плоской фигуры, тела).
studopedia.ru
Вероятность события

Глава 3
Вероятность - второе фундаментальное понятие в теории вероятностей после случайного события. С помощью него строятся все вероятностные схемы случайных явлений.
Вероятность реального события есть мера его объективной возможности. Это определение вероятности скорее философское, чем математическое. Для того, чтобы понятие вероятности стало математическим, нужно ввести его как количественную характеристику событий. Математических определений вероятности существует несколько. Все они прошли длительный путь развития, дополняют и обобщают друг друга. Формирование понятия вероятности не закончено до сих пор. Исторически несомненно, что вероятность появилась как идеальное понятие, отражающее свойства относительной частоты при массовых статистических исследованиях.
3.1 Относительная частота события и ее свойства
Рассмотрим опыт E, который можно повторять неоднократно (теоретически - неограниченное число раз). В результате опыта может появиться событие A.
Определение. Относительной частотой события A называется отношение числа µ опытов, в которых появилось событие A, к общему числу n проведенных опытов.
Относительная частота события A обозначается символом P (A). Таким образом,
P (A) = µn.
Практика указывает на то, что для широкого круга явлений при неограниченном увеличении числа опытов n относительная частота события стабилизируется, приближаясь к некоторому постоянному числу, в том смысле, что большие отклонения ее от этого числа наблюдаются тем реже, чем больше n.
Так, при бросании монеты относительная частота выпадений орла колеблется около числа 1/2.
Относительная частота имеет следующие свойства:
1.P (I) = 1, так как µ = n.
2.P ( ) = 0, так как µ = 0.
3.0 ≤ P (A) ≤ 1, так как 0 ≤ µ ≤ n, 0 ≤ µn ≤nn.
14

4. P (A + B) = P (A) + P (B), если A и B несовместны, так как
P (A + B) = µ1 + µ2 =µ1 +µ2 = P (A) + P (B).n n n
Здесь µ1 - число опытов, в которых появилось событие A, µ2 - то же для события B. Так как события A и B несовместны, то число опытов, в которых появилась сумма A + B, равно µ1 + µ2.
3.2Статистическое определение вероятности
Пусть опыт E проводится многократно в стабильных условиях, в результате чего наблюдается событие A и вычисляется его относительная частота.
Определение. Вероятностью события называется число, около которого колеблется относительная частота этого события, приближаясь к нему при увеличении числа опытов.
Вероятность события A обозначается символом P (A). Это идеальная характеристика события, отражающая свойства относительной частоты, поэтому вероятности приписываются те же свойства 1-4,что имеются у относительной частоты:
1.P (I) = 1.
2.P ( ) = 0.
3.0 ≤ P (A) ≤ 1.
4.P (A + B) = P (A) + P (B), если A и B несовместны.
Замечание. Статистическое определение вероятности не дает однозначного способа вычисления вероятности события (в этом его несовершенство), но дает возможность найти
оценку этой вероятности:
P (A) ≈ P (A) = µn.
Чем больше n, тем точнее это приближенное равенство. На практике за вероятность события принимается относительная частота этого события при достаточно большом числе n проведенных опытов.
3.3Аксиоматическое определение вероятности
Напомним, что элементарным событием ω называется непосредственный исход эксперимента E. Множество всех элементарных событий образует пространство элементарных событий Ω. Под событием в аксиоматической схеме понимается сумма (объединение) какого-либомножества элементарных событий ωi:
X
A = ωi.
i
Пример. E - бросание игральной кости, A - событие, означающее выпадение четного числа очков. A = ω2 + ω4 + ω6, где ωi - элементарное событие, означающее выпадение i очков.
15

Все рассматриваемые в схеме события образуют множество событий F , называемое полем (Field), иначе - алгеброй, к которому предъявляются следующие требования, обеспечивающие применение понятия вероятности:
1.F содержит достоверное и невозможное события.
2.Если события A1, A2, . . . (конечное или счетное множество) принадлежат F , то F принадлежат сумма, произведение и дополнение этих событий.
Понятие вероятности строится для всех событий алгебры F .
Аксиоматическое определение вероятности. Вероятностью называется числовая функция P (A) события A, определенная на алгебре F , имеющая свойства 1-4:
X X
1) P (I) = 1; 2) P ( ) = 0; 3) 0 ≤ P (A) ≤ 1; 4) P Ak = P (Ak), если события
k k
A1, A2, . . . (конечное или счетное множество) попарно несовместны.
3.4 Классическое определение вероятности
События называются равновозможными, если по условиям эксперимента ни одно из этих событий не является предпочтительным по отношению к другим с точки зрения возможности их появления.
Определение. Эксперимент E назовемклассическим, если он приводит к множеству событий, удовлетворяющих трем условиям:
1.они попарно несовместны;
2.образуют полную группу;
3.равновозможные.
Эти события называются случаями илиисходами и обозначаются ω. Они могут быть элементарными событиями.
Определение. Исход ω называетсяблагоприятным (иначе - благоприятствующим) событию A, если ω влечет A: ω A.
Определение. Если эксперимент E является классическим, то вероятностью события A называется отношение числа m исходов, благоприятствующих событию A, к общему числу n исходов.
Классическое определение, в отличие от аксиоматического, является конструктивным и дает следующую меру возможности события:
P (A) = mn .
Легко проверяется, что вероятность события, определенная по классической схеме, удовлетворяет свойствам 1-4,которые в общем случае объявлены аксиомами, а здесь следуют из формулы.
Недостатком классического определения является его малая применимость, так как классические эксперименты встречаются редко - в искусственно созданных ситуациях.
Пример. Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента - разрядники?
16

Пусть событие А - 3 выбранных наудачу студентов - разрядники. Общее число случаев выбора 3 студентов из 30 равно n = C303 , так как комбинации из 30 студентов по 3 представляют собой сочетания, ибо отличаются только составом студентов. Точно так же число случаев, благоприятствующих событию A, равно m = C103 . Итак,
|
P (A) = |
m |
= |
10 · 9 · 8 |
: |
30 · 29 · 28 |
= |
61 |
≈ |
0, 030. |
||||||||||
|
n |
1 |
· |
2 |
· |
3 |
1 |
· |
2 |
· |
3 |
203 |
||||||||
Пример. В лифт на1-мэтаже девятиэтажного дома вошли 4 человека, каждый из которых может выйти независимо друг от друга на любом этаже с2-гопо9-й.Какова вероятность того, что все пассажиры выйдут: а) на6-мэтаже; б) на одном этаже?
а) Пусть событие A - все пассажиры выйдут на 6-мэтаже. Каждый пассажир может выйти со2-гопо9-йэтаж 8 способами. По правилу произведения общее число способов выхода четырех пассажиров из лифта равно n = 8 · 8 · 8 · 8 = 84. Число случаев, благоприятствующих событию A, равно m = 1. Таким образом,
|
P (A) = |
m |
= |
1 |
= 0, 00024. |
|
n |
4 |
|||
|
8 |
б) Пусть событие B - все пассажиры выйдут на одном этаже. Теперь событию B будут благоприятствовать m = 8 случаев (все пассажиры выйдут или на 2-мэтаже, или на3-м,
..., или на 9-мэтаже). Поэтому
|
P (B) = |
m |
= |
8 |
= |
1 |
= 0, 00195. |
|
|
n |
4 |
3 |
|||||
|
8 |
8 |
||||||
3.5 Геометрическое определение вероятности
Рассмотрим на оси абсцисс отрезок Q и внутри него отрезок q : q Q.
Рис. 3.1: Иллюстрация геометрического определения вероятности
На отрезке Q случайно выбирается точка X. Этот выбор можно интерпретировать как бросание случайной точки X на отрезок Q. При этом попадание X на Q считается достоверным событием, а попадание на отрезок q - случайным. Далее предполагается, что равновозможно попадание X на q, где бы отрезок q ни находился внутри отрезка Q при условии, что длина q - фиксирована. Пусть событие A = (X q). Тогда по определению
P (A) = µ(q) . µ(Q)
Здесь µ - мера множества, а в данном случае мера отрезка - его длина.
17

Данная формула распространяется на плоский и пространственный случаи, но тогда под мерой понимается соответственно площадь или объем рассматриваемых областей.
Вероятность, определенная из геометрических соображений, также обладает всеми четырьмя свойствами, присущими другим определениям вероятности.
Понятие меры в математике также является аксиоматически определяемым. Мерой, заданной на некотором множестве называется неотрицательная функция, обладающая следующими свойствами:
1.Для любого элемента множества мера неотрицательна и однозначно определена.
2.Мера аддитивна, т.е. для объединения непересекающихся элементов множества мера будет равна сумме мер слагаемых.
Пример. Два лица А и В условились встретиться в определенном месте, договорившись только о том, что каждый является туда в любой момент времени между 11 и 12ч и ждет в течение 30 мин. Если партнер к этому времени еще не пришел или уже успел покинуть установленное место, встреча не состоится. Найти вероятность того, что встреча состоится.
Рис. 3.2: Геометрическая вероятность
Обозначим моменты прихода в определенное место лиц А и В соответственно через x и y. В прямоугольной системе координат Oxy возьмем за начало отсчета 11ч, а за единицу измерения - 1ч. По условию 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Этим неравенством удовлетворяют координаты любой точки, принадлежащей квадрату OKLM со стороной, равной 1 (рис. 3.2). Событие C - встреча двух лиц - произойдет, если разность между x и y не превзойдет 0,5ч (по абсолютной величине), т.е. |y − x| ≤ 0, 5.
Решение последнего неравенства есть полоса x − 0, 5 ≤ y ≤ x + 0, 5, которая внутри квадрата на рис.3.2 представляет заштрихованную область g. По формуле геометрической
18
вероятности
|
1 − 2 · |
1 |
· 0, 52 |
||||
|
P (C) = |
µ(g) |
= |
Sg |
= |
2 |
= 0, 75, |
|
12 |
||||||
|
µ(G) |
SG |
|||||
так как площадь области g равна площади квадрата G без суммы площадей двух угловых (не заштрихованных) треугольников.
19
StudFiles.ru
Классическое определение вероятности
Пусть произведено некоторое испытание. Каждый из возможных результатов испытания назовем элементарным исходом(элементарным событием). Те элементарные исходы, в которых интересующее нас событие наступает, назовемблагоприятными исходами. Предположим, что все элементарные исходы несовместны, равновозможны и образуют полную группу.
Определение. Вероятностью события![]() назовем отношение числа благоприятных этому событию исходов испытания к общему числу всех равновозможных несовместных элементарных событий, образующих полную группу:
назовем отношение числа благоприятных этому событию исходов испытания к общему числу всех равновозможных несовместных элементарных событий, образующих полную группу:
![]() ,
,
![]() – число благоприятных исходов,
– число благоприятных исходов,
![]() – общее число элементарных исходов.
– общее число элементарных исходов.
Свойство 1.Вероятность достоверного события равна 1.
Д оказательство.Если событие достоверно, то
оказательство.Если событие достоверно, то![]() и
и![]() .
.
Свойство 2.Вероятность невозможного события равна 0.
Д оказательство.Если событие невозможно, то
оказательство.Если событие невозможно, то![]() и
и![]() .
.
Свойство 3.Вероятность случайного события есть положительное число, заключенное между 0 и 1:![]() .
.
Итак, вероятность любого события удовлетворяет соотношению:
![]() .
.
Основные формулы комбинаторики
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов какого-либо конечного множества. При вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее часто употребляемые из них.
Перестановками называют комбинации, состоящие из одних и тех же![]() различных элементов и отличающихся только порядком их расположения. Число всех возможных перестановок равно:
различных элементов и отличающихся только порядком их расположения. Число всех возможных перестановок равно:
![]() .
.
По определению ![]() .
.
Пример 6.
Сколькими способами можно разместить на полке 5 книг?
Решение.![]() .
.
Размещенияминазывают комбинации, составленные из![]() различных элементов по
различных элементов по![]() элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений равно:
элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений равно:
![]() .
.
Пример 7.
Учащемуся необходимо сдать 4 экзамена на протяжении 8 дней. Сколькими способами это можно сделать?
Решение.![]() .
.
Сочетаниями называют комбинации, составленные из![]() различных элементов по
различных элементов по![]() элементов, которые отличаются хотя бы одним элементом. Число сочетаний равно:
элементов, которые отличаются хотя бы одним элементом. Число сочетаний равно:
![]() .
.
Пример 8.
Сколькими способами из 30 человек можно выбрать комиссию, состоящую из 3 человек?
Решение. ![]() .
.
Свойства:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() (число всех подмножеств из
(число всех подмножеств из![]() элементов равно
элементов равно![]() ).
).
При решении задач комбинаторики используют следующее основное правило комбинаторики(правило умножения):
Пусть требуется выполнить одно за другим ![]() действий. Если первое действие можно выполнить
действий. Если первое действие можно выполнить![]() способами, второе –
способами, второе –![]() способами и т.д.,
способами и т.д.,![]() -е действие –
-е действие –![]() способами, то все
способами, то все![]() действий вместе могут быть выполнены
действий вместе могут быть выполнены![]() способами.
способами.
Пример 9.
 Из Киева до Новгорода можно добраться
Из Киева до Новгорода можно добраться![]() способами.
способами.
Пример 10.
Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если цифры не повторяются?
Решение.6 цифр, 0 не может быть первой цифрой. Отсюда имеем:
![]() чисел.
чисел.
Пример 11.
Учащемуся необходимо сдать 4 экзамена за 8 дней. Сколькими способами это можно сделать, если известно, что последний экзамен будет сдаваться на восьмой день?
Решение.
![]() .
.

Пример 12.
В некотором государстве нет двух одинаковых по количеству и расположению зубов жителей. Указать максимально возможное количество жителей этого государства.
Решение.
I способ.
 беззубый 1
беззубый 1
с 1-м зубом 32
![]()
с 3-мя зубами ![]()
……………….
с 32-мя зубами ![]()
IIспособ.
2 способа заполнения каждой ячейки. Всю челюсть можно заполнить
способа заполнения каждой ячейки. Всю челюсть можно заполнить
![]()
 .
.
32 раза
StudFiles.ru
Классическое определение вероятности.
Как было сказано выше, при большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A , т.е. .
Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности).
Два события называются равновероятными (или равновозможными ), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.
Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
События E 1 , E 2 , ..., E N в данном опыте образуют полную группу , если в результате опыта должно произойти хотя бы одно из них.
Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.
Очевидно, любое событие A и противоположное ему событие образуют полную группу.
Событие B называется благоприятствующим событию A , если наступление события B влечет за собой наступление события A .
Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A .
Пусть события E 1 , E 2 , ..., E N в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N . Итак, мы приходим к следующему определению.
Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
Это определение вероятности часто называют классическим . Можно показать, что классическое определение удовлетворяет аксиомам вероятности.
Пример 1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным. ( Решение )
Пример 2. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность р того, что оба шара окажутся белыми? ( Решение )
Пример 3. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара? ( Решение )
Геометрическое определение вероятности . Пусть в некоторую область случайным образом бросается точка T , причем все точки области W равноправны в отношении попадания точки T . Тогда за вероятность попадания точки T в область A принимается отношение
[image] , (1.5)
где S ( A ) и S (W) — геометрические меры (длина, площадь, объем и т.д.) областей A и W соответственно.
Условная вероятность.
Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной ; если же налагаются и другие дополнительные условия, то вероятность события называют условной . Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А .
Условной вероятностью (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
.
Вчастности,отсюдаполучаем
.
Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий , то вероятность события А вычисляется по формуле
.
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий , вероятности появления которых . Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами. Тогда по формуле полной вероятности
Если событие А произошло, то это может изменить вероятности гипотез .
По теореме умножения вероятностей
,
откуда
.
Аналогично, для остальных гипотез
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез называются апостериорными вероятностями, тогда как - априорными вероятностями.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.
Числовые характеристики дискретных случайных величин
Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины .
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
,
где – возможные значения случайной величины , а – соответствующие вероятности.
Замечание. Вышеприведенная формула справедлива для дискретной случайной величины, число возможных значений которой конечно. Если же случайная величина имеет счетное число возможных значений, то для нахождения математического ожидания используют формулу:
,
причем это математическое ожидание существует при выполнении соответствующего условия сходимости числового ряда в правой части равенства.
Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной:
.
2. Постоянный множитель можно вынести за знак математического ожидания:
.
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
.
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
.
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Пусть производится независимых испытаний, в каждом из которых вероятность появления события постоянна и равна . Тогда справедлива следующая теорема.
Теорема. Математическое ожидание числа появлений события в независимых испытаниях равно произведению числа испытаний на вероятность появления этого события в каждом испытании:
.
Разность между случайной величиной и ее математическим ожиданием называется отклонением .
Теорема. Математическое ожидание отклонения равно нулю:
.
Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величиной от ее математического ожидания:
.
Дисперсия имеет размерность, равную квадрату размерности случайной величины.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
.
Свойства дисперсии
1. Дисперсия постоянной величины равно нулю:
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
.
3. Дисперсия суммы двух независимых случайных величин равно сумме дисперсий этих случайных величин:
.
Следствие. Дисперсия суммы нескольких взаимно независимых случайных величин равно сумме дисперсий этих величин.
4. Дисперсия разности двух независимых случайных величин равно сумме дисперсий этих случайных величин:
.
Теорема. Дисперсия числа появлений события в независимых испытаниях, в каждом из которых вероятность появления события постоянна, равна произведению числа испытаний на вероятность появления и вероятность непоявления этого события в одном испытании:
.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
.
Размерность среднего квадратического отклонения совпадает с размерностью самой случайной величины.
Законы распределения дискретных случайных величин
Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения.
При табличном способе задания закона распределения первая строка таблицы содержит возможные значения случайной величины (обычно в порядке возрастания), а вторая – соответствующие вероятности ( ):
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Бернулли: Дискретная случайная величина имеет биномиальный закон распределения (закон распределения Бернулли), если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, …, n с вероятностями, вычисляемыми по формуле Бернулли:
| xi | … | m | … | n | ||
| pi | qn | … | … | pn |
где q=1-p ; - число сочетаний из n элементов по m .
Пример 2. На некотором участке дороги 60% водителей соблюдают предусмотренный правилами скоростной режим. Составить закон распределения числа водителей, соблюдающих установленные ограничения по скорости, из пяти проехавших.
Случайная величина Х – число водителей, соблюдающих установленные ограничения по скорости из пяти проехавших. В n=5 независимых испытаниях вероятность того, что скоростной режим не нарушен, по условию постоянна и равна: p=0,6 . Следовательно, вероятность нарушения: q=1-0,6=0,4 . Тогда биномиальный закон распределения числа водителей имеет вид:
| xi | ||||||
| pi | 0,01024 | 0,0768 | 0,2304 | 0,3456 | 0,2592 | 0,07776 |
Пуассона: Дискретная случайная величина имеет закон распределенияПуассона с параметром , если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, … с вероятностями, вычисляемыми по формуле Пуассона. Т. к. вероятность наступления события в каждом испытании мала (при ), закон распределения Пуассона еще называют законом редких событий.
| xi | … | m | … | |
| pi | … | … |
Пример 3. Вероятность попадания в цель при одном выстреле равна 0,015. Сделано 600 выстрелов. Какова вероятность того, что число попаданий в цель не меньше 7 и не большее 10?
В данном случае . Предполагая закон распределения Пуассона, имеем:
| xi | |||
| pi | 0,1171 | 0,1318 | 0,1186 |
Следовательно, .
studopedia.ru
Читайте также
![Закон джоуля ленца формула и определение Закон джоуля ленца формула и определение]() Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение![Акт определение Акт определение]() Акт определение
Акт определение![Двигатель определение Двигатель определение]() Двигатель определение
Двигатель определение![Определение цены деления шприца Определение цены деления шприца]() Определение цены деления шприца
Определение цены деления шприца![Определение высоты объекта Определение высоты объекта]() Определение высоты объекта
Определение высоты объекта![Определение ph воды Определение ph воды]() Определение ph воды
Определение ph воды![Легальное определение юридического лица дано Легальное определение юридического лица дано]() Легальное определение юридического лица дано
Легальное определение юридического лица дано![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Деталь определение Деталь определение]() Деталь определение
Деталь определение![Машина определение Машина определение]() Машина определение
Машина определение![Места массового скопления людей определение Места массового скопления людей определение]() Места массового скопления людей определение
Места массового скопления людей определение![Определение надежности Определение надежности]() Определение надежности
Определение надежности
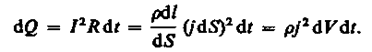 Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение Акт определение
Акт определение Двигатель определение
Двигатель определение Определение цены деления шприца
Определение цены деления шприца Определение высоты объекта
Определение высоты объекта Определение ph воды
Определение ph воды Легальное определение юридического лица дано
Легальное определение юридического лица дано Болезнь определение
Болезнь определение Деталь определение
Деталь определение Машина определение
Машина определение Места массового скопления людей определение
Места массового скопления людей определение Определение надежности
Определение надежности