Случайные величины
Определение. Случайной величиной называют такую величину, которая в результате эксперимента принимает какое-либо одно значение из множества ее возможных значений, причем до эксперимента невозможно предсказать, какое именно.
Случайными величинами являются, например, количество очков, выпадающих при бросании игрального кубика, число посетителей аптеки в течение дня, количество яблок на дереве и т. д.
Случайными величинами являются также температура больного в некоторое наугад выбранное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента и т. д.
О![]()
![]()
![]() днако с математической точки зрения между такими случайными величинами, как, например, число посетителей аптеки в течение дня (обозначим эту случайную величину X1) и рост наугад выбранного студента из некоторой группы студентов (величина Х2), имеется принципиальное различие, а именно: для величины X1можно перечислить все ее возможные значения (1, 2, 3, 4, 5, 6, ...), тогда как для величины Х2этого сделать нельзя, поскольку эта величина в результате измерения может принять любое значение из отрезка, где
днако с математической точки зрения между такими случайными величинами, как, например, число посетителей аптеки в течение дня (обозначим эту случайную величину X1) и рост наугад выбранного студента из некоторой группы студентов (величина Х2), имеется принципиальное различие, а именно: для величины X1можно перечислить все ее возможные значения (1, 2, 3, 4, 5, 6, ...), тогда как для величины Х2этого сделать нельзя, поскольку эта величина в результате измерения может принять любое значение из отрезка, где
и — соответственно минимальный и максимальный рост студентов группы.
Случайные величины принято обозначать прописными буквами латинского алфавита — X, Y, Z и т. д., а их возможные значения — соответствующими строчными буквами с числовыми индексами. Например, значения случайной величины xобозначают следующим образом:x1,x2,x3и т. д.
Понятие дискретных и непрерывных случайных величин
Определение. Случайная величина называется дискретной, если совокупность всех ее возможных значений представляет собой конечное или бесконечное, но обязательно счетное множество значений, т. е. такое множество, все элементы которого могут быть (по крайней мере, теоретически) пронумерованы и выписаны в соответствующей последовательности.
Определение. Случайная величина называется непрерывной, если множество ее возможных значений представляет собой некоторый конечный или бесконечный промежуток числовой оси.
Исходя из этих определений, такие из перечисленных выше случайных величин, как количество очков, выпадающих при бросании игрального кубика, число посетителей аптеки в течение дня, количество яблок на. дереве, являются дискретными случайными величинами, а такие, как температура больного в фиксированное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента, — непрерывными величинами.
Дискретные случайные величины
Рассмотрим подробнее дискретные случайные величины, причем, как правило, будем ограничивать рассмотрение такими случайными величинами, у которых количество возможных значений конечно.
Наиболее полную информацию о дискретной случайной величине дает закон распределения этой величины.
Определение. Законом распределения дискретной случайной величины называется соответствие между всеми возможными значениями этой случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины часто задают в виде двухстрочной таблицы, в первой строке которой перечислены все возможные значения этой величины (как правило, в порядке возрастания), а во второй — соответствующие этим значениям вероятности таблице 1:
|
X |
X1 |
X2 |
… |
Xn |
|
P |
P1 |
P2 |
… |
Pn |
Пример 2.Имеется десять студенческих групп, насчитывающих соответственно 12, 10, 11, 8, 12, 9, 10, 8, 10 и 11 студентов. Составить закон распределения случайной величины X, определяемой как число студентов в наугад выбранной группе.
Решение. Возможными значениями рассматриваемой случайной величины Х являются следующие (в порядке возрастания):
8, 9, 10, 11 и 12.
Поскольку случайная величина Х принимает значение, равное 8, в том случае, если наугад выбранной группой окажется группа из 8 студентов (назовем это событием А), вероятность того, что случайная величина Х примет значение ![]() , равна вероятности этого случайного события:
, равна вероятности этого случайного события:![]() .
.
Вероятность же случайного события А в соответствии с классическим определением вероятности равна ![]() поскольку из 10 групп две насчитывают по 8 студентов.
поскольку из 10 групп две насчитывают по 8 студентов.
Таким образом, для вероятности значения ![]() получаем:
получаем:
![]() .
.
Аналогично можно найти вероятности остальных значений случайной величины X:
![]()
что позволяет составить искомый закон распределения (таблица 2):
|
X |
8 |
9 |
10 |
11 |
12 |
|
P |
0,2 |
0,1 |
0,3 |
0,2 |
0,2 |
Закон распределения дискретной случайной величины может быть задан также с помощью формулы, позволяющей для каждого возможного значения этой величины определить соответствующую вероятность.
StudFiles.ru
Дискретные и непрерывные случайные величины
Как правило, при изготовлении продукции на процесс её производства оказывает влияние множество различных факторов, в результате чего наблюдается разброс значений показателей качества продукцию. Таким образом, показатели качества изготовляемой продукции или оказываемых услуг следует рассматривать как случайные величины.
Случайной величиной называется такая величина, которая в результате испытаний в границах определенного интервала может принимать различные числовые значения (согласно СТБ ГОСТ Р 50779.10 случайная величина - переменная, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей).
Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные значения и не могут принимать значения промежуточные между ними. Например, количество негодных деталей в партии может быть только целым положительным числом 1, 2, 3 и т.д., но не может быть 1,3; 1,7 и т.п.
Непрерывной случайной величинойназывается такая величина, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала.
Например, действительные размеры деталей, обработанных на станке, являются случайными величинами непрерывного типа, так как они могут принять любое численное значение в определенных границах.
Возможности случайных величин принимать при испытаниях те или иные численные значения оцениваются при помощи вероятностей.
Совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей для каждого из значений, называется распределением случайных величин(согласно СТБ ГОСТ Р 50779.10 распределение – это функция, определяющая вероятность того, что случайная величина примет какое-либо заданное значение или будет принадлежать заданному множеству значений).
Распределение случайной величины можно представить в табличном, графическом виде и при помощи статистических оценок.
При представлении распределения случайной величины в табличном виде каждому номеру исследуемой единицы продукции (номеру измерения) соответствует значение показателя качества для данной единицы продукции (результат измерения).
При представлении распределения случайной величины в графическом виде строят график распределения в координатах значение случайной величины – вероятность (частота, частость) значения случайной величины.
На рисунке ниже показаны графики распределения дискретной и непрерывной случайных величин.
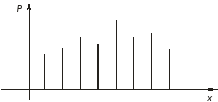
Рисунок - График распределения дискретной случайной величины
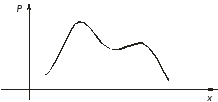
Рисунок - График распределения непрерывной случайной величины
Различают теоретические и эмпирические распределения случайных величин. В теоретических распределениях оценка возможных значений случайной величины производится при помощи вероятностей, а в эмпирических — при помощи частот или частостей, полученных в результате испытаний.
Следовательно, эмпирическим распределением случайной величиныназывается совокупность экспериментальных ее значений, расположенных в порядке возрастания, с указанием частот или частостей для каждого из значений(согласно СТБ ГОСТ Р 50779.10 распределение частот – это эмпирическое отношение между значениями признака и его частотами или его относительными частотами).
Таблица. Пример табличного представления теоретического распределения дискретной случайной величины
|
X |
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
P(X) |
P(X1) |
P(X2) |
P(X3) |
P(X4) |
P(X5) |
P(Xi)=1 |
Таблица. Пример табличного представления эмпирического распределения дискретной случайной величины
|
X |
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
mx |
1/30 |
3/30 |
15/30 |
6/30 |
5/30 |
mxi=1 |
Графически эмпирическое распределение дискретной случайной величины можно представить в виде столбиковой диаграммы, образуемой набором столбцов равной ширины, высоты которых пропорциональны частотам дискретных значений случайной величины.
Рисунок - Столбиковая диаграмма дискретной случайной величины.
Если случайная величина является непрерывной, то возникают некоторые сложности с представлением ее распределения в виде таблицы или графика. Поэтому на практике при изучении случайных величин непрерывного типа полученные значения разбивают на равные интервалы с таким расчетом, чтобы значение интервала было несколько больше погрешности измерения исследуемой величины. Затем подсчитывают частоты не по действительным значениям случайной величины, а по интервалам. Поэтому таблица эмпирического распределения случайной величины непрерывного типа будет иметь следующий вид.
Таблица. Эмпирическое распределение случайной величины непрерывного типа.
|
Интервал значений Х |
Среднее арифметическое значение |
Частота fi |
Частость mi |
|
160,031 - 160,033 |
160,032 |
3 |
0,03 |
|
160,033 - 160,035 |
160,034 |
3 |
0,03 |
|
160,035 - 160,037 |
160,036 |
5 |
0,05 |
|
160,037 - 160,039 |
160,038 |
26 |
0,26 |
|
160,039 - 160,041 |
160,040 |
31 |
0,31 |
|
160,041 - 160,043 |
160,042 |
19 |
0,19 |
|
160,043 - 160,045 |
160,044 |
8 |
0,08 |
|
160,045 - 160,047 |
160,046 |
5 |
0,05 |
|
fi= 100 |
mi= 1 |
Эмпирическое распределение случайной непрерывной величины графически может быть представлено в виде гистограммы распределения, полигона частот или полигона кумулятивных частот.
Гистограмма распределения представляет собой совокупность соприкасающихся прямоугольников, основания которых равны интервалам разбиения непрерывной случайной величины, а площади пропорциональны частотам, с которыми значения случайной величины попадают в эти интервалы (согласно СТБ ГОСТ Р 50779.10 гистограмма (распределения) – это графическое представление распределения частот для количественного признака, образуемое соприкасающимися прямоугольниками, основаниями которых служат интервалы классов, а площади пропорциональны частотам этих классов).

Рисунок - Гистограмма распределения случайной непрерывной величины.
Полигон частот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны серединам интервалов разбиения, а ординаты – соответствующим частотам.
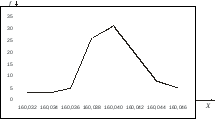
Рисунок - Полигон частот случайной непрерывной величины.
Полигон кумулятивных частот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам интервалов разбиения, а ординаты – либо кумулятивным частотам, либо кумулятивным частостям (кумулятивным относительным частотам).
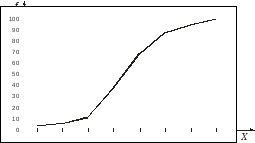
Рисунок - Полигон кумулятивных частот случайной непрерывной величины.
При теоретических описаниях случайных величин непрерывного типа используется функция распределения. Теоретическое распределение случайной непрерывной величины графически может быть представлено в виде интегральной, обратной интегральной, дифференциальной функций распределения и функции интенсивности.
Пусть Х — случайная величина, а х — какое-либо действительное число (при этом Х < х). Событию Х < х отвечает вероятность Р(Х < х), которая является функцией F(х), т.е.
Р(Х < х) = F(х)
F(Х) называется функцией распределения вероятностей случайной величины или интегральной функцией распределения.
Для дискретной случайной величины интегральная функция распределения F(Х) легко определяется по таблице или графику.
Таким образом, для приведенного выше примера распределения дискретной случайной величины (при Х < 4):
F(X) = Р(Х) = P(Х=1) + P(Х=2) + P(Х=3) = 1/30 + 4/30 +15/30 = 19/30
График интегральной функции распределения дискретной случайной величины будет иметь вид ступенчатой кривой. Ординаты кривой для любого значения Х будут представлять сумму вероятностей предшествующих значений.

Рисунок - Интегральная функция распределения дискретной случайной величины
Вероятность того, что случайная величина при испытаниях окажется в границах двух заданных значений х1 и х2 (х2 > х1) равна приращению интегральной функции на этом участке, т.е.
Р(х1≤ Х ≤ х2) = Р(Х < х2) — Р(Х < х1) = F(Х2) — F(Х1)
Если обратиться к выше приведенному примеру распределения дискретной случайной величины, то при х1= 2 и х2 = 3:
Р(2≤Х≤3) = Р(Х < 3) — Р(Х < 2)= F(Х2) — F(Х1)= 4/30—1/30 = 3/30
Для непрерывной случайной величины график интегральной функции распределения будет иметь вид монотонно возрастающей кривой. На практике с помощью интегральной функции распределения определяют теоретические частоты распределения.

Рисунок - Интегральная функция распределения
непрерывной случайной величины
Обратная интегральная функция распределения равна разности между единицей и интегральной функции распределения.
Плотностью распределения (дифференциальной функцией распределения) случайной величины называют первую производную от интегральной функции распределения:
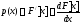
Для аналитического описания непрерывной случайной величины в теории надежности используют функцию интенсивности, равную отношению дифференциальной функции распределения к обратной интегральной функции распределения:
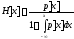

Рисунок - Функция интенсивности непрерывной случайной величины.
StudFiles.ru
Тема 3.
Случайные величины и функции распределения
Понятие случайной величины.
Понятие случайной величины
Функция распределения случайной величины, ее свойства
Случайные величины с дискретным распределением
Понятие случайной величины с дискретным распределением
Закон распределения дискретной случайной величины.
Примеры дискретных распределений
Случайные величины с абсолютно непрерывным распределением
Понятие случайной величины с абсолютно непрерывным распределением
Закон распределения абсолютно непрерывной случайной величины. Плотность, ее свойства
Примеры абсолютно непрерывных распределений
Понятие случайного вектора.
Понятие случайного вектора
Независимые случайные величины
Совместное распределение случайных величин
Понятие случайной величины.
С момента возникновения теории вероятностей ее основной задачей было изучение не вероятностных свойств экспериментов со случайными исходами, а связанных с этими экспериментами числовых величин, которые естественно назвать случайными величинами. Например, мы можем интересоваться не парами чисел на верхних гранях кубиков, а их суммой; числом успехов или числом неудач до первого успеха в схеме Бернулли.
Часто в литературе можно встретить вариации на тему следующего определения: Случайной величиной называют переменную величину, которая в зависимости от исходов испытания принимает значения, зависящие от случая.
Таким образом, случайная величина – это числовая величина, значение которой зависит от того, какой именно (элементарный) исход произошел в результате эксперимента со случайным исходом. Множество всех значений, которые случайная величина может принимать, называют множеством возможных значений этой случайной величины.
Мы приведем более строгое определение, поскольку понятие случайной величины является одним из тех ключевых понятий, которые связывают теорию вероятностей с математическим анализом и составляют понятийную основу математической статистики.
Определение. Случайной величиной называется функция Х = Х(ω), определенная на пространстве элементарных событий Ω, для которых событие {Х < х} = {ω: Х(ω) < х} принадлежит σ-алгебре событий A для любого вещественного х.
Условие {Х < х} єA дает возможность рассматривать вероятности событий {Х < х}, поскольку вероятности определены только на множествах из А. Кроме того, через события {Х < х}, х є (-∞, ∞ ) с помощью известных операций над событиями можно выразить сколь угодно сложное событие, связанное со случайной величиной Х. Такое событие также будет принадлежать σ-алгебре событий A и, следовательно, для него определена вероятность.
Замечание. Таким образом, случайная величина – это функция, областью определения которой является пространство элементарных событий Ω, а множеством значений – числовое множество, возможно, все множество действительных чисел R.
σ-алгебра событий A – это область определения вероятности, если рассматривать ее как функцию.
Замечание. «Термин «случайная величина» несколько неточен, более подходящим был бы термин «Функция случая» , независимой переменной является точка в пространстве элементарных событий, т.е. исход эксперимента или случай». (В.Феллер «Введение в теорию вероятностей», гл. IX)
Случайные величины обозначаются буквами греческого алфавита:(кси),(эта), или заглавными буквами латинского алфавита X, Y, …Значения случайной величины будем записывать в виде конечной или бесконечной последовательностиx1,x2,,xn,; y1,y2,,yn,
Замечание. Ранее мы ввели понятие вероятности применительно к некоторым событиям. Теперь мы переходим к разговору о функциях. Самое очевидное событие, которое можно связать с понятием функции – это принятие ею некоторого значения (конкретного или принадлежащего промежутку)
Для исследования вероятностных свойств случайной величины необходимо знать правило, позволяющее находить вероятность того, что случайная величина примет значение из подмножества ее значений. Любое такое правило называют законом распределения вероятностей или распределением (вероятностей) случайной величины. (при этом слово «вероятностей» обычно опускают)
Общим законом распределения, присущим всем случайным величинам, является функция распределения.
Определение. Вся совокупность вероятностей Р{Х < х}, х є (-∞, ∞ ) задает закон распределения случайной величины Х в общем случае. Часто для краткости закон распределения случайной величины называют просто распределением случайной величины.
Определение. Функция F(x) = Р{Х < х}, х є (-∞, ∞ ) называется функцией распределения случайной величины Х.
Значение функции распределения в точке х равно вероятности события {Х < х}, то есть события, состоящего из тех и только тех элементарных исходов ω, для которых Х < х.
Обычно говорят, что значение функции распределения в точке х равно вероятности того, что случайная величина Х примет значение, меньшее х.
Геометрически это означает следующее: F(x) – вероятность того, что случайная величина Х примет значение, которое изображается точкой на числовой прямой, расположенной слева от точки х.
Замечание. Функцию распределения называют также интегральной функцией, или интегральным законом распределения случайной величины Х
Функция распределения обладает следующими свойствами:
-
0≤ F(x)≤1 (т.к. по определению, функция распределения является вероятностью)
-
F(x1 ) ≤ F(x2 ) при x1 < x2 (т.е. F(x) – неубывающая функция)
-
lim F(x) = 0 при x → - ∞ , lim F(x) = 1 при x → + ∞
-
P (x1 ≤ X ≤ x2) = F(x1 ) - F(x2)
-
F(x) – непрерывная слева функция, т.е. F(x) = F(x - 0), где F(x - 0) = lim F(y) при y → x - 0 (левосторонний предел)
Замечание. Для того, чтобы подчеркнуть, какой именно случайной величине принадлежит функция распределения F(x), этой функции иногда приписывают нижний индекс, обозначающий конкретную случайную величину. Например, FX(x) = Р{Х < х}
Замечание. В некоторых изданиях функция распределения определяется как F(x) = Р{Х ≤ х}. Такое определение ничего не меняет по существу понятия функции распределения, меняется лишь последнее, пятое свойство. Функция в таком случае оказывается непрерывной справа.
Отступление: «Что такое функция?»
Пусть нам даны два множества Х и Y, причем Y – числовое множество. И пусть задано правило f, по которому каждому элементу (точке) множества Х ставится в соответствие (один и только один) элемент (число) множества Y. Правило f вместе с множествами X и Y задают функцию f. Запись y=f(x) означает, что к некоторой точке x множества X применили правило f, и в результате получили точку y из множества Y. X называется аргументом (независимой переменной), а y – значением (зависимой переменной) функции f в точке х. Множество Х называется областью определения (областью задания) функции, говорят, что функция задана на этом множестве, множество Y называется множеством значений функции. Множество Х совершенно необязательно является числовым множеством. Так, случайная величина – это функция , заданная на нечисловом пространстве элементарных событий.
StudFiles.ru
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, причем какое именно заранее неизвестно.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями. Этот закон задается в виде таблицы, формулы или графика.
Для дискретных случайных величин одним из наиболее употребительных является так называемый биномиальный закон распределения, к которому приводит схема Бернулли повторения испытаний. Формула (8) и является аналитическим выражением этого закона.
Пример 11.
По каналу связи передается сообщение с помощью кода, состоящего из двух знаков. Вероятность появления первого равна 2/3. Передано три знака. Найти закон распределения для появлений первого знака.
Решение.
По условию n=4, р=2/3, q=1/3. Возможные значения числа появлений первого знака: 0, 1, 2 и 3. Найдем их вероятности по формуле (8):
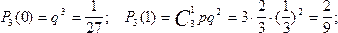
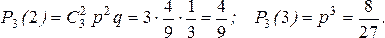
Этот закон можно представить в виде таблицы
| X | ||||
| P1/27 | 1/27 | 2/9 | 4/9 | 8/27 |
Функцией распределения называют функцию, определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньше х, то есть
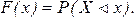 (13)
(13)
Геометрически это означает, что случайная величина с вероятностью р примет значение, которое на числовой оси изображается точкой, лежащей левее х.
Для непрерывной случайной величины функция распределения есть непрерывная кусочно-дифференцируемая функция. Из определения выводятся основные свойства:
1. Значения функции распределения принадлежат отрезку [0,1], т.е.
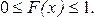
2. F(x) - неубывающая функция, то есть 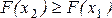 , если
, если 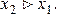
3. Вероятность того, что случайная величина примет значение, заключенное на промежутке [а,b[, равна приращению функции распределения на этом промежутке
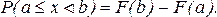 (14)
(14)
Для непрерывной случайной величины вероятность принять отдельное значение равно нулю. Поэтому для непрерывных случайных величин
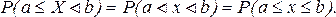
Пример 12.
Случайная величина Х задана функцией распределения
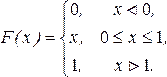
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее отрезку [-1;0,5].
Решение.
Из условия следует, что Х - непрерывная случайная величина, которая может принимать значение от 0 до 1.
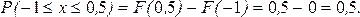
Плотностью распределения вероятностей непрерывнойслучайной величины Х называют первую производную от функции распределения
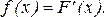 (15)
(15)
Функция распределения F(x) есть одна из первообразных для плотности распределения. Исходя из определения плотности или дифференциального закона распределения и ее связи с функцией распределения, легко показать следующие свойства:
1. Плотность распределения непрерывной случайной величины - неотрицательная функция 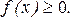
2. Вероятность попадания случайной величины Х в интервал равна
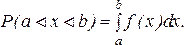 (16)
(16)
3. Из свойства 2 получим выражение для функции распределения
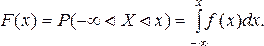 (17)
(17)
4. Условие нормировки
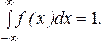 (18)
(18)
Пример 13.Дискретная величина Х задана таблицей
| Х | ||||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
Найти функцию распределения и построить ее график.
Решение.
1. Если 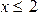 , то
, то 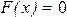 , так как Х не может принимать значение меньше 2.
, так как Х не может принимать значение меньше 2.
2. Пусть 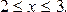

В этом случае в интервал (-¥, х) попадает только одно значение случайной величины Х (X=2). Поэтому
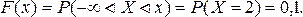
3. Пусть 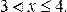
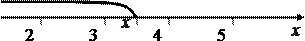
Для любого значения аргумента х функции F(x), удовлетворяющего данному неравенству, в интервал (-¥, х) попадает два значения случайной величины (X=2 и X=3). Поскольку события, что Х примет данные значения являются несовместными (или X =2 или X =3), то
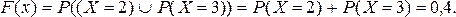
4. Аналогично если 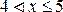
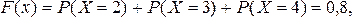
а при 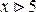
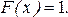
Следовательно, функция распределения будет иметь вид
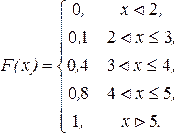
Строим график функции распределения

Рис. 1 - График функции распределения
дискретной случайной величины
Пример 14. Плотность распределения ошибки измерения
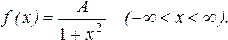
Определить значение коэффициента А и построить график f(x). Найти функцию распределения и построить ее график. Вычислить вероятность того, что ошибка измерения примет значение, заключенное в интервале 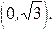
Решение.
Значение коэффициента А легко определить из условия 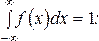
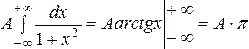 .
.
Приравнивая  получаем
получаем 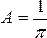 .
.
Функцию распределения F(x) находим по определению
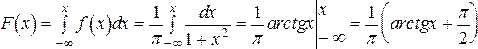 .
.
Вероятность того, что случайная величина попадет в указанный интервал, можно вычислить двумя способами:
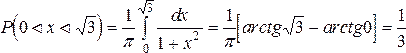
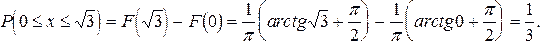
Строим графики функций

Любой закон распределения случайной величины полностью характеризует ее с вероятностной точки зрения. Однако для практики достаточно бывает указать отдельные числовые характеристики случайной величины, по которым можно судить об особенностях ее распределения. К этим характеристикам относятся среднее или математическое ожидание М(x), дисперсия D(x) и среднее квадратическое отклонение s(x). Две последние величины описывают рассеяние случайной величины относительно среднего.
Для дискретной случайной величины математическое ожиданиеопределяется как сумма произведений всех ее возможных значений на их вероятности.
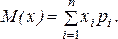 (19)
(19)
Для непрерывной случайной величины:
 (20)
(20)
Дисперсиейслучайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
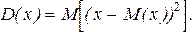 (21)
(21)
Часто бывает удобно пользоваться другой формулой для вычисления дисперсии
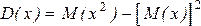 , (22)
, (22)
где 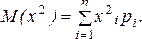 (23)
(23)
для дискретной случайной величины и
 (24) для непрерывной случайной величины.
(24) для непрерывной случайной величины.
Размерность дисперсии равна квадрату размерности случайной величины, что на практике не всегда удобно. Поэтому наряду с дисперсией для характеристики рассеяния используется корень квадратный из дисперсии, называемый средним квадратическим отклонением.
 (25)
(25)
Пример 15. Для случайной величины, заданной в примере 11, найти M(x), D(x) и s(x).
Решение
а) В примере 11 закон распределения дискретной случайной величины задан таблицей:
| Х | ||||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
По формуле (19) получим
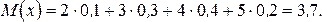
Для определения дисперсии по формуле (22) составим таблицу для случайной величины x2 .
| x2 | ||||
| p | 0,1 | 0,3 | 0,4 | 0,2 |
Тогда
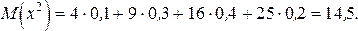

Пример 16. Найти числовые характеристики M(x), D(x), s(x) и постоянную С для равномерно распределенной случайной величины, плотность распределения которой имеет вид:
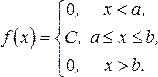
Решение.
Из условия нормировки определим С.
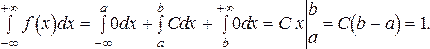
Откуда
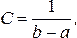
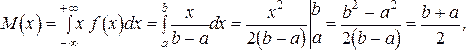
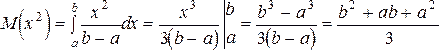 ,
,
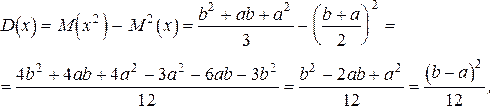
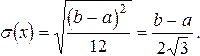
Из всех законов распределения непрерывных случайных величин нормальный закон наиболее часто встречается в практике. Плотность распределения нормального закона может быть записана в виде
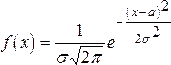 , (26)
, (26)
где s>0 и а — параметры распределения, равные среднему квадратическому отклонению и математическому ожиданию данной случайной величины, соответственно. Вероятность попадания нормально распределенной случайной величины Х в интервал (a,b) вычисляется по формуле
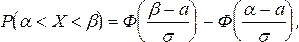 (27)
(27)
где Ф(х) — функция Лапласа (см. формулу (11)).
Вероятность заданного отклонения от математического ожидания можно найти с помощью более простой формулы
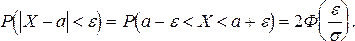 (28)
(28)
Пример 17.Радиолокатор измеряет дальность до цели с систематическими и случайными ошибками. Систематическая ошибка равна 10 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением 25 м. Найти вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 40 м, а также вероятность того, что измеренная дальность не превзойдет истинную.
Решение.
Случайная величина X (ошибка измерения дальности) распределена по нормальному закону.
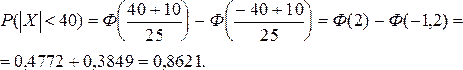
Вероятность того, что измеренная дальность не превзойдет истинную, равна:

studopedia.ru
Дискретная случайная величина, определение
M@shinist71
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Дадим более точное определение :
Дискретной случайной величиной (ДСВ) называют такую величину, множество значений которой либо конечное, либо бесконечное, но счетное.
Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.
Читайте также
![Коэффициент корреляции может принимать значения Коэффициент корреляции может принимать значения]() Коэффициент корреляции может принимать значения
Коэффициент корреляции может принимать значения![Бит может принимать значения Бит может принимать значения]() Бит может принимать значения
Бит может принимать значения![Сколько в россии городов федерального значения Сколько в россии городов федерального значения]() Сколько в россии городов федерального значения
Сколько в россии городов федерального значения![Значением логической переменной может быть Значением логической переменной может быть]() Значением логической переменной может быть
Значением логической переменной может быть![Сколько городов федерального значения в рф Сколько городов федерального значения в рф]() Сколько городов федерального значения в рф
Сколько городов федерального значения в рф![Дискретные значения Дискретные значения]() Дискретные значения
Дискретные значения![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского- 7 Треф значение
![Славянские имена мальчиков и их значение Славянские имена мальчиков и их значение]() Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия![Амбициозный значение слова Амбициозный значение слова]() Амбициозный значение слова
Амбициозный значение слова
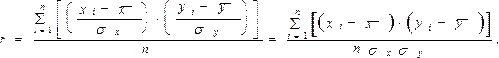 Коэффициент корреляции может принимать значения
Коэффициент корреляции может принимать значения Бит может принимать значения
Бит может принимать значения Сколько в россии городов федерального значения
Сколько в россии городов федерального значения Значением логической переменной может быть
Значением логической переменной может быть Сколько городов федерального значения в рф
Сколько городов федерального значения в рф Дискретные значения
Дискретные значения Аутентичность значение слова
Аутентичность значение слова Чувак значение слова с еврейского
Чувак значение слова с еврейского Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение Барыга значение слова википедия
Барыга значение слова википедия Амбициозный значение слова
Амбициозный значение слова