Коэффициент корреляции
статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции

10. Проверка гипотезы о наличии линейной связи между зависимой и независимой переменной.
Приведенные ранее показатели качества подгонки не позволяют принять окончательного статического решения по пригодности РУ. Такие решения принимаются на основе стат.критериев. Одним из таких критериев является F-критерий (F статистика). После оценки свободного члена регрессии (а) и коэффициента регрессии (в) выдвигается гипотеза о том, что линейная связь между х и у не подтверждается. 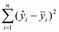
Близкое к 0 значение этой суммы свидетельствует об отсутствии какой либо тенденции для у в связи с изменениями х. Если Fрасч>Fтабл, то гипотезу об отсутствии лин.связи отвергаем с вероятностью р.
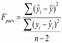 Fтабл берется из таблицы распределения Фишера, для степеней свободы n1 и n2. n1=k, n2=n-2
Fтабл берется из таблицы распределения Фишера, для степеней свободы n1 и n2. n1=k, n2=n-2
k-количество факторов в модели
n- количество наблюдений.
Отдельно исследуется коэффициент регрессии, выдвигается гипотеза что Х влияет на У не существенно. Выдвинутая гипотеза равноценна тому что b=0 на всей генеральной совокупности.
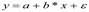
Если наша гипотеза верна то t-статистика или t-критерий подчиняется t-распределению со степенью свободы n-2
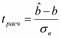 . Где
. Где  - стандартная ошибка коэффициента b.
- стандартная ошибка коэффициента b.
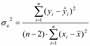 Аналогично находим tтабл если tрасч >tтабл. То гипотезу что b=0 отвергаем, значит b не равен 0, если наоборот то принимаем гипотезу, t- статистика используется также при построении доверительного интервала для коэффициента т.е. b. Областью правдоподобных значений является (-t;t)
Аналогично находим tтабл если tрасч >tтабл. То гипотезу что b=0 отвергаем, значит b не равен 0, если наоборот то принимаем гипотезу, t- статистика используется также при построении доверительного интервала для коэффициента т.е. b. Областью правдоподобных значений является (-t;t)

11. Проверка существенности влияния фактора на результативную переменную.
12. Общая процедура проверки выполнения условий для получения «хороших» оценок методом наименьших квадратов.
Метод наименьших квадратов дает «хорошие» оценки коэффициентов регрессии при выполнении некоторых условий. Эти условия касаются случайные компоненты 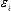 .
.
Для однофакторной модели это след.условия:
1) 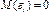 2)
2) 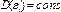 3)
3) 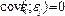
В многофакторной модели добавляются следующие условия:
4) это независимость факторов между собой т.е.

13. Выполнение предпосылки МНК о случайном характере остатков модели.
Метод наименьших квадратов дает «хорошие» оценки коэффициентов регрессии при выполнении некоторых условий. Эти условия касаются случайные компоненты 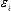 .
.
Для однофакторной модели это след.условия:
1) 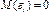 2)
2) 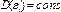 3)
3) 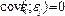
В многофакторной модели добавляются следующие условия:
4) это независимость факторов между собой т.е.

Условие:
 1)
1) 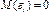 при нарушении условия оценка параметров регрессионной модели является неэффективной. Графически нарушение этого условия можно изобразить:
при нарушении условия оценка параметров регрессионной модели является неэффективной. Графически нарушение этого условия можно изобразить:
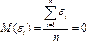
Метод наименьших квадратов при отсутствии ошибок в расчетах всегда дает выражение данного условия.
2) 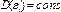 - разброс точек на плоскости.
- разброс точек на плоскости.
 Нарушение условия 2) когда дисперсия случайной компоненты не является постоянной, можно на графике изобразить следующим образом:
Нарушение условия 2) когда дисперсия случайной компоненты не является постоянной, можно на графике изобразить следующим образом:
Если остатки имеют постоянную дисперсию, то они называются гомаскедастичными, являются называются гомоскедастичностью. Если остатки непостоянны, то они называются гетероскедостичными, а явление называется гетероскедастичностью.
Гетероскедастичность приводит к тому, что коэффициенты регрессии не представляют собой лучшие оценки или не являются оценками с наименьшей дисперсией. Следовательно они не являются «хорошими» коэффициентами. Непостоянство дисперсий часто встречается в моделях нестационарной экономики(Рссия), когда в качестве исходных данных используется временные ряды стоимостных показателей. В пространстве выборках гетероскедастичность встречается когда анализируемые объекты не однородны по своему масштабу. Гетероскедичность ведет к тому что стандартные ошибки будут смещенными, решение о наличии гетероскедичности принимается на основе общей процедуры проверки гипотез. Один из критериев F-критерий
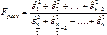
Данный F-критерий имеет F – распределение со степенями свободы
n1=n/2-k, n2=n/2-k
При этих степенях свободы находим Fтабл, сравнивая Fрасч с Fтабл
1) если Fрасч попадает в интервал 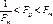 то дисперсия пост-а
то дисперсия пост-а
2) если Fр >Fт, то дисперсия уменьшается
3) если Fр т то дисперсия увеличивается
14. Выполнение предпосылки МНК о нулевом математическом ожидании.
3) 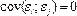
Нарушение условия проявляются в том, что м/у ошибками разных наблюдений есть какая то зависимость. Графически нарушение этого условия можно представить:
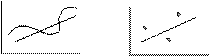
Нарушение условия независимости остатков м/у собой называется автокорреляцией остатков,имеет место когда текущее значение уi . Нарушение 3-го условия независимости остатков делает модель неадекватной. Вызвано это тем что при наличии автокорелляции стандарт ошибки модели будут недооценены. И как следствие проверка значимости коэффициентов регрессии будет ненадежной. Проверку на наличие автокорелляции проводят на основе теста Дарвина-Уотсона (статистика критерий Д-У)
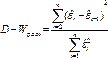 Данный критерий может принимать значение от 0 до 4. При проверке наличии автокорреляции на практике можно руководствоваться след. Простым правилом: расчетное значение D-W близкое к 2 свидетельствует об отсутствии автокорелляции, к 4 – об отсутствии, к 0- о положит. Автокорреляции.
Данный критерий может принимать значение от 0 до 4. При проверке наличии автокорреляции на практике можно руководствоваться след. Простым правилом: расчетное значение D-W близкое к 2 свидетельствует об отсутствии автокорелляции, к 4 – об отсутствии, к 0- о положит. Автокорреляции.
Строгие решения принимаются из правил:
1) если 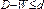 то гипотеза об отсутствии автокорелляции отвергается.
то гипотеза об отсутствии автокорелляции отвергается.
2) если 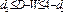 то гипотеза об отсут автокорел-и принимается
то гипотеза об отсут автокорел-и принимается
3) 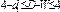 принимается гипотеза о том, что отрицательная автокорелляция
принимается гипотеза о том, что отрицательная автокорелляция
4) если  то гипотеза о наличии автокорреляции не принимается и не отвергается .
то гипотеза о наличии автокорреляции не принимается и не отвергается .
15. Выполнение предпосылки МНК о гомоскедостичности остатков. Тест Голдфилда-Кванта.
Условие независимости факторов м/у собой.
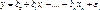
Нарушение данного условия, когда факторы зависят друг от друга, называется мультиколлинеарностью. Нарушение условия 4 является нарушением одного из требований классической регрессии. Мультиколлинеарность проверяется на основе коэффициента корреляции 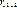
Для того чтобы мультиколлинеарности не было д.б. 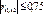
Мультиколлениарность возникает из-за неисправного выбора списка объясняющих переменных или из за эконом.природы выбранных переменных.
Внешние признаками мультиколлениарности явл.следующие признаки:
1) наличие значений коэффициентов парной корреляции м/у объясняющими переменными, превышающих по модулю 0,75.
2) Наличие оценок коэффициентов регрессии, имеющих непрерывные знаки.
3) Существенные изменения значений коэффициентов регрессии при небольшом изменении исходных данных.
4) Наличие больших стандартных ошибок и малой статической значимости коэффициентов регрессии при общей значимости модели.
Для устранения мультиколлениарностисуществует несколько способов:
1. исключение из модели связанных м/у собой независимых переменных путем отбора наиболее существенных объясняющих переменных.
использование методов оценки коэффициентов, учитывающих мультиколлениарность
Явление гетероскедастичности возникает, как правило, при анализе неоднородных объектов. Например, при построении зависимости прибыли фирмы от размера основного фонда (или каких-либо других факторов) гетероскедастичность вызвана тем, что у больших фирм колебания прибыли будут выше, чем у малых.
МНК при наличии гетероскедастичности позволяет получить несмещенные оценки параметров модели, но оценка дисперсии ошибки, и, следовательно, границы доверительных интервалов оценок параметров модели и прогноза зависимой переменной будут неверными, т.к. они вычисляются на основании предположения гомоскедастичности ошибок.
Для проверки на гетероскедастичность существует большое число тестов. Мы остановимся на тесте Голдфельда-Квандта.
Тест Голдфелъда-Квандта применяется в том случае, когда имеются предположения:
1.о прямой зависимости дисперсии σt, ошибки регрессии εt от величины некоторой независимой переменной X в наблюдении t;
2.случайный член εt, распределен нормально и не подвержен автокорреляции.
Алгоритм теста:
1.Упорядочивание n данных в выборке по величине независимой переменной, относительно которой есть подозрение на гетероскедастичность.
2.Исключение с средних наблюдений в этом упорядочении в целях построения двух независимых "частных" регрессий по данным n' = (n-с)/2 в начале выборки и по данным n' = (n - с)/2 в конце выборки
3.Проведение двух независимых "частных" регрессий - первых n' и последних n' наблюдений и построение соответствующих остатков е1 и е2;
4.Вычисление сумм квадратов остатков "частных" регрессий: е1'е1, е2'е2. Если предположение относительно природы гегероскедастичности верно, то дисперсии ошибок регрессии в последних n' наблюдениях будут больше (меньше), чем в первых n' наблюдениях при прямой (обратной) пропорциональной зависимости между σt и Xt и это скажется на сумме квадратов остатков в рассматриваемых частных регрессиях. Поэтому в качестве теста на выявление гетероскедастичности остатков регрессии предлагается использовать статистику F, вид которой определяется предположением зависимости между дисперсией ошибок регрессии σt и регрессором Xt:
F = е1'е1 / е2'е2- в случае обратной пропорциональности
F = е2'е2 / е1'е1- в случае прямой пропорциональности.
Статистика F имеет распределение Фишера с (n'- k- 1) степенями свободы, где k- число объясняющих переменных в регрессионном уравнении. Если значение статистики превышает критически значение при определенном уровне значимости, то нулевая гипотеза Н0 об отсутствии гетероскедастичности отвергается.
Тест ранговой корреляции Голдфелда-Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности.
При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е.
s2 = fi (xi), 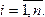 (1)
(1)
Чаще всего функция f выбирается квадратичной, что соответствует тому, что средняя квадратичная ошибка регрессии зависит от наблюдаемых значений регрессоров приближенно линейно. Гомоскедастичной выборке соответствует случай f = const.
16. Выполнение предпосылки МНК о гомоскедостичности остатков. Тест ранговой корреляции Спирмена.
При использовании данного теста
предполагается, что дисперсии отклонений
остатков будут монотонно изменятьcя
(увеличиваться или уменьшаться) с увеличением
фактора пропорциональности Z. Поэтому значения ei и zi будут коррелированы (возможно, нелинейно!).
studopedia.ru
Коэффициент корреляции
 Коэффициент корреляции – это величина, которая может варьировать в пределах от +1 до –1. В случае полной положительной корреляции этот коэффициент равен плюс 1 (говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной), а при полной отрицательной – минус 1 (свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются).
Коэффициент корреляции – это величина, которая может варьировать в пределах от +1 до –1. В случае полной положительной корреляции этот коэффициент равен плюс 1 (говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной), а при полной отрицательной – минус 1 (свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются).
 Пр1.:
Пр1.:
График зависимости застенчивости и дипресивности. Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны.
 Пр2.: График для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)
Пр2.: График для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)
 В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников.
Используется две системы классификации корреляционных связей по их силе: общая и частная.
Общая классификация корреляционных связей:1) сильная, или тесная при коэффициенте корреляции r>0,70;2) средняя при 0,500,70, а не просто корреляция высокого уровня значимости.В следующей таблице написаны названия коэффициентов корреляции для различных типов шкал.
| Дихотомическая шкала (1/0) | Ранговая (порядковая) шкала | Интервальная и абсолютная шкала | |
| Дихотомическая шкала (1/0) | Коэфициент ассоциации Пирсона, коэффициент четырехклеточной сопряженности Пирсона. | Рангово-бисериальная корреляция. | Бисериальная корреляция |
| Ранговая (порядковая) шкала | Рангово-бисериальная корреляция. | Ранговый коэффициент корреляции Спирмена или Кендалла. | Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент |
| Интервальная и абсолютная шкала | Бисериальная корреляция | Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент | Коэффициент корреляции Пирсона (коэффициент линейной корреляции) |
При r=0линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общими средними, а линии регрессии параллельны осям координат.
Равенство r=0говорит лишь об отсутствии линейной корреляционной зависимости (некоррелированности переменных), но не вообще об отсутствии корреляционной, а тем более, статистической зависимости.
Иногда вывод об отсутствии корреляции важнее наличия сильной корреляции. Нулевая корреляция двух переменных может свидетельствовать о том, что никакого влияния одной переменной на другую не существует, при условии, что мы доверяем результатам измерений.
В SPSS: 11.3.2 Коэффициенты корреляции
До сих пор мы выясняли лишь сам факт существования статистической зависимости между двумя признаками. Далее мы попробуем выяснить, какие заключения можно сделать о силе или слабости этой зависимости, а также о ее виде и направленности. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения — большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.
В качестве коэффициента корреляции между переменными, принадлежащими порядковой шкале применяется коэффициент Спирмена, а для переменных, принадлежащих к интервальной шкале — коэффициент корреляции Пирсона (момент произведений). При этом следует учесть, что каждую дихотомическую переменную, то есть переменную, принадлежащую к номинальной шкале и имеющую две категории, можно рассматривать как порядковую.
Для начала мы проверим существует ли корреляция между переменными sex и psyche из файла studium.sav. При этом мы учтем, что дихотомическую переменную sex можно считать порядковой. Выполните следующие действия:
· Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
· Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
· Щелкните на кнопке Statistics... (Статистика). В диалоге Crosstabs: Statistics установите флажок Correlations (Корреляции). Подтвердите выбор кнопкой Continue.
· В диалоге Crosstabs откажитесь от вывода таблиц, установив флажок Supress tables (Подавлять таблицы). Щелкните на кнопке ОК.
Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:
studopedia.ru
/ СПСС 10
Задание № 10 Корреляционный анализ
Понятие корреляции
Корреляция или коэффициент корреляции – это статистический показательвероятностнойсвязи между двумя переменными, измеренными по количественным шкалам. В отличие от функциональной связи, при которой каждому значению одной переменной соответствуетстрого определенноезначение другой переменной,вероятностная связьхарактеризуется тем, что каждому значению одной переменной соответствуетмножество значенийдругой переменной, Примером вероятностной связи является связь между ростом и весом людей. Ясно, что один и тот же рост может быть у людей разного веса и наоборот.
Корреляция представляет собой величину, заключенную в пределах от -1 до + 1, и обозначается буквой r. Причем, если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой. Значение корреляции менее 0,2 рассматривается как слабая корреляция, свыше 0,5 – высокая. Если коэффициент корреляции отрицательный, это означает наличие обратной связи: чем выше значение одной переменной, тем ниже значение другой.
В зависимости от принимаемых значений коэффициента rможно выделить различные виды корреляции:
Строгая положительная корреляцияопределяется значениемr=1. Термин «строгая» означает, что значение одной переменной однозначно определяются значениями другой переменной, а термин «положительная» - что с возрастанием значений одной переменной значения другой переменной также возрастают.
Строгая корреляция является математической абстракцией и практически не встречается в реальных исследованиях.
Положительная корреляция соответствует значениям 0
Отсутствие корреляцииопределяется значениемr=0. Нулевой коэффициент корреляции говорит о том, что значения переменных никак не связаны между собой.
Отсутствие корреляции Ho: 0rxy=0формулируется как отражениенулевой гипотезы в корреляционном анализе.
Отрицательная корреляция: -1
Строгая отрицательная корреляцияопределяется значениемr= -1. Она также, как и строгая положительная корреляция, является абстракцией и не находит выражение в практических исследованиях.
Таблица 1
Виды корреляции и их определения
|
Виды |
Определения |
|
Строгая положительная корреляция |
r=1 |
|
Положительная корреляция |
0< r |
|
Отсутствие корреляции |
r=0. |
|
Отрицательная корреляция |
-1 |
|
Строгая отрицательная корреляция |
r= -1 |
Метод вычисления коэффициента корреляции зависит от вида шкалы, по которой измерены значения переменной.
Коэффициент корреляции rПирсонаявляется основным и может использоваться для переменных с номинальной и частично упорядоченными, интервальными шкалами, распределение значений по которым соответствует нормальному (корреляция моментов произведения). Коэффициент корреляции Пирсона дает достаточно точные результаты и в случаях анормальных распределений.
Для распределений, не являющихся нормальными, предпочтительнее пользоваться коэффициентами ранговой корреляции Спирмена и Кендалла. Ранговыми они являются потому, что программа предварительно ранжирует коррелируемые переменные.
Корреляцию rСпирмена программаSPSSвычисляет следующим образом: сначала переменные переводятся в ранги, а затем к рангам применяется формулаrПирсона.
В основе корреляции, предложенной М. Кендаллом, лежит идея о том, что о направлении связи можно судить, попарно сравнивая между собой испытуемых. Если у пары испытываемых изменение по Х совпадают по направлению с изменением по Yсовпадает, то это свидетельствует о положительной связи. Если не совпадает – то об отрицательной связи. Данный коэффициент применяется преимущественно психологами, работающими с малыми выборками. Так как социологи работают с большими массивами данных, то перебор пар, выявление разности относительных частот и инверсий всех пар испытуемых в выборке затруднителен. Наиболее распространенным является коэф. Пирсона.
Поскольку коэффициент корреляции rПирсона является основным и может использоваться (с некоторой погрешностью в зависимости от типа шкалы и уровня анормальности в распределении) для всех переменных, измеренных по количественным шкалам, рассмотрим примеры его использования и сравним полученные результаты с результатами измерений по другим коэффициентам корреляции.
Формула вычисления коэффициента r- Пирсона:
rxy= ∑ (Xi-Xср)∙(Yi-Yср) / (N-1)∙σx∙σy∙
Где: Xi, Yi- Значения двух переменных;
Xср, Yср- средние значения двух переменных;
σx,σy– стандартные отклонения,
N- количество наблюдений.
Парные корреляции
Например, мы хотели бы выяснить, как соотносятся ответы между различными видами традиционных ценностей в представлениях студентов об идеальном месте работы (переменные: а9.1, а9.3, а9.5, а9.7), а затем о соотношении либеральных ценностях (а9.2, а9.4. а9.6, а9.8) . Данные переменные измерены по 5 – членным упорядоченным шкалам.
Используем процедуру: «Анализ», «Корреляции»,«Парные». По умолчанию коэф. Пирсона установлен в диалоговом окне. Используем коэф. Пирсона
.В окно отбора переносятся тестируемые переменные: а9.1, а9.3, а9.5, а9.7
Путем нажатия ОК получаем расчет:
Корреляции
|
а9.1.т. Насколько важно иметь достаточно времени для семьи и личной жизни? |
а9.3.т. Насколько важно не бояться потерять свою работу? |
а9.5.т. Насколько важно иметь такого начальника, который будет советоваться с Вами, принимая то или иное решение ? |
а9.7.т. Насколько важно работать в слаженном коллективе, ощущать себя его частью? |
||
|
а9.1.т. Насколько важно иметь достаточно времени для семьи и личной жизни? |
Корреляция Пирсона |
1 |
,138(**) |
,040 |
,157(**) |
|
Знч.(2-сторон) |
,003 |
,389 |
,001 |
||
|
N |
458 |
452 |
458 |
451 |
|
|
а9.3.т. Насколько важно не бояться потерять свою работу? |
Корреляция Пирсона |
,138(**) |
1 |
,202(**) |
,188(**) |
|
Знч.(2-сторон) |
,003 |
,000 |
,000 |
||
|
N |
452 |
460 |
459 |
453 |
|
|
а9.5.т. Насколько важно иметь такого начальника, который будет советоваться с Вами, принимая то или иное решение ? |
Корреляция Пирсона |
,040 |
,202(**) |
1 |
,193(**) |
|
Знч.(2-сторон) |
,389 |
,000 |
,000 |
||
|
N |
458 |
459 |
465 |
458 |
|
|
а9.7.т. Насколько важно работать в слаженном коллективе, ощущать себя его частью? |
Корреляция Пирсона |
,157(**) |
,188(**) |
,193(**) |
1 |
|
Знч.(2-сторон) |
,001 |
,000 |
,000 |
||
|
N |
451 |
453 |
458 |
460 |
** Корреляция значима на уровне 0.01 (2-сторон.).
Таблица количественных значений построенной корреляционной матрицы
|
Признаки |
Количество |
|
Размер корреляционной матрицы |
4×4 |
|
Количество коэффициентов корреляции |
6 |
|
Количество значимых коэффициентов корреляции (при Р |
5 |
|
В т.ч. с положительной связью |
5 |
|
В т.ч. с отрицательной связью |
0 |
Частные корреляции:
Для начала построим парную корреляцию между указанными двумя переменными:
|
Корреляции |
|||
|
с8. Ощущают близость с теми, кто живет рядом с вами, соседями |
с12. Ощущают близость со своей семьей |
||
|
с8. Ощущают близость с теми, кто живет рядом с вами, соседями |
Корреляция Пирсона |
1 |
,120** |
|
Знч.(2-сторон) |
,001 |
||
|
N |
718 |
698 |
|
|
с12. Ощущают близость со своей семьей |
Корреляция Пирсона |
,120** |
1 |
|
Знч.(2-сторон) |
,001 |
||
|
N |
698 |
748 |
|
|
**. Корреляция значима на уровне 0.01 (2-сторон.). |
|||
Затем используем процедуру построения частной корреляции: «Анализ», «Корреляции»,«Частные».
Предположим, что ценность «Важно самостоятельно определять и изменять порядок своей работы» во взаимосвязи с указанными переменными окажется тем решающим фактором, под влияние которого ранее выявленная связь исчезнет, либо окажется малозначимой.
|
Корреляции |
||||
|
Исключенные переменные |
с8. Ощущают близость с теми, кто живет рядом с вами, соседями |
с12. Ощущают близость со своей семьей |
||
|
с16. Ощущают близость с людьми, котрые имеют тот же достаток, что и вы |
с8. Ощущают близость с теми, кто живет рядом с вами, соседями |
Корреляция |
1,000 |
,102 |
|
Значимость (2-сторон.) |
. |
,012 |
||
|
ст.св. |
0 |
599 |
||
|
с12. Ощущают близость со своей семьей |
Корреляция |
,102 |
1,000 |
|
|
Значимость (2-сторон.) |
,012 |
. |
||
|
ст.св. |
599 |
0 |
||
Как видно из таблицы под влиянием контрольной переменной связь несколько снизилась: с 0, 120 до 0, 102. Однако, это незначительно снижение не позволяет утверждать, что ране выявленная связь является отражением ложной корреляции, т.к. она остается достаточно высокой и позволяет с нулевой погрешностью опровергать нулевую гипотезу.
StudFiles.ru
Коэффициент корреляции это:
Коэффициент корреляцииКорреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными, называется корреляционным анализом.
Содержание
|
Коэффициент корреляции
Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике — это показатель характера изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R и может принимать значения между -1 и +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи (при коэффициенте корреляции равном единице говорят о функциональной связи), а если ближе к 0, то слабой.
Коэффициент корреляции Пирсона
Для метрических величин применяется коэффициент корреляции Пирсона, точная формула которого была введена Фрэнсисом Гальтоном:
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
![\R_{X,Y} = \frac{\mathrm{cov}(X,Y)}{\sqrt{\mathrm{D}[X]} \cdot \sqrt{\mathrm{D}[Y]}}](http://i.zna4enie.ru/1/znachenie-kojefficienta-korreljacii_10.png) ,
,
где cov обозначает ковариацию, а D — дисперсию, или, что то же самое,
![\R_{X,Y} = \frac{\mathbb{E}[XY]-\mathbb{E}X \cdot \mathbb{E}Y} {\sqrt{(\mathbb{E}[X^2]-(\mathbb{E}X)^2)} \cdot \sqrt{ (\mathbb{E}[Y^2]-(\mathbb{E}Y)^2)}}](http://i.zna4enie.ru/1/znachenie-kojefficienta-korreljacii_11.png) ,
,
где символ 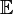 обозначает математическое ожидание.
обозначает математическое ожидание.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона (корреляция моментов произведений). Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена или τ (тау) Кендала. В случае, когда одна из двух переменных является дихотомической, используется точечная двухрядная корреляция, а если обе переменные являются дихотомическими: четырёхполевая корреляция. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена).
Коэффициент корреляции Кенделла
Используется для измерения взаимной неупорядоченности.
Коэффициент корреляции Спирмена
Свойства коэффициента корреляции
- Неравенство Коши — Буняковского:
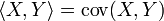 , то норма случайной величины будет равна
, то норма случайной величины будет равна ![\|X\| = \sqrt{\mathrm{D}[X]}](http://i.zna4enie.ru/a/znachenie-kojefficienta-korreljacii_14.png) , и следствием неравенства Коши — Буняковского будет:
, и следствием неравенства Коши — Буняковского будет: 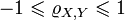 .
.
- Коэффициент корреляции равен
 тогда и только тогда, когда X и Y линейно зависимы:
тогда и только тогда, когда X и Y линейно зависимы:
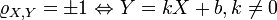 , где
, где 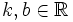 . Более того в этом случае знаки
. Более того в этом случае знаки 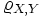 и k совпадают:
и k совпадают: 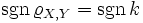 .
.
- Если X,Y независимые случайные величины, то
 . Обратное в общем случае неверно.
. Обратное в общем случае неверно.
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей.
Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б: если обе переменные растут то корреляция положительная, если одна переменная растёт, а вторая уменьшается, корреляция отрицательная.
Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = sin(x) и B = cos(x), то он будет близок к нулю, т. е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону sin2(x) + cos2(x) = 1.
Ограничения корреляционного анализа
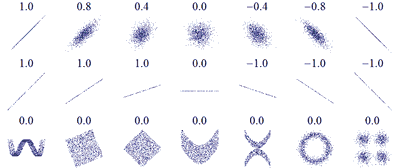 Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
Графики распределений пар (x,y) с соответствующими коэффициентами корреляций x и y для каждого из них. Обратите внимание, что коэффициент корреляции отражает линейную зависимость (верхняя строка), но не описывает кривую зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка).
- Применение возможно в случае наличия достаточного количества случаев для изучения: для конкретного вида коэффициента корреляции составляет от 25 до 100 пар наблюдений.
- Второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных. Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов просто ввиду того, что зависимость нелинейна (выражена, например, в виде параболы).
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например, ввиду действия третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Ложная корреляция
Часто заманчивая простота корреляционного исследования подталкивает исследователя делать ложные интуитивные выводы о наличии причинно-следственной связи между парами признаков, в то время как коэффициенты корреляции устанавливают лишь статистические взаимосвязи.
В современной количественной методологии социальных наук, фактически, произошел отказ от попыток установить причинно-следственные связи между наблюдаемыми переменными эмпирическими методами. Поэтому, когда исследователи в социальных науках говорят об установлении взаимосвязей между изучаемыми переменными, подразумевается либо общетеоретическое допущение, либо статистическая зависимость.
См. также
- Автокорреляционная функция
- Взаимнокорреляционная функция
- Ковариация
- Коэффициент детерминации
- Регрессионный анализ
Wikimedia Foundation. 2010.
dic.academic.ru
Линейный коэффициент корреляции
При расчете этого показателя учитываются величины отклонений индивидуальных значений признака от средней, т.е. соответственно для факторного и результативного признаков величины 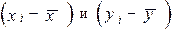 . Однако непосредственно сопоставлять между собой данные абсолютные величины нельзя. Признаки могут быть выражены в разных единицах, а при одинаковых единицах измерения средние могут быть различны по величине. Сравнению подлежат отклонения, выраженные в долях среднего квадратического отклонения (нормированные отклонения). Рассчитывают среднее произведение нормированных отклонений, которое называется линейным коэффициентом корреляции:
. Однако непосредственно сопоставлять между собой данные абсолютные величины нельзя. Признаки могут быть выражены в разных единицах, а при одинаковых единицах измерения средние могут быть различны по величине. Сравнению подлежат отклонения, выраженные в долях среднего квадратического отклонения (нормированные отклонения). Рассчитывают среднее произведение нормированных отклонений, которое называется линейным коэффициентом корреляции:
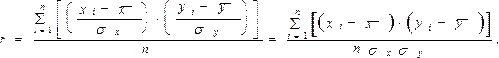
где 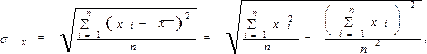
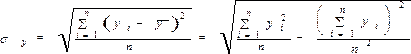
Выполнив несложные преобразования, можно получить следующую формулу для расчета линейного коэффициента корреляции:

При пользовании этой формулой отпадает необходимость вычислять отклонения индивидуальных значений признаков от средней величины, что исключает ошибку в расчетах при округлении средних величин.
Линейный коэффициент корреляции может принимать любые значения в пределах от -1 до + 1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи. Прямой зависимости соответствует знак плюс, а обратной зависимости - знак минус. Линейный коэффициент корреляции применяется для измерения тесноты связи только при линейной форме связи. Равенство 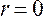 говорит лишь об отсутствии линейной корреляционной зависимости, но не вообще об отсутствии корреляционной, а тем более статистической зависимости. Величина коэффициента корреляции не является доказательством наличия причинно-следственной связи между исследуемыми признаками, а является оценкой степени взаимной согласованности в изменениях признаков. Установлению причинно-следственной зависимости предшествует анализ качественной природы явлений. Особенно осторожно следует подходить к истолкованию полученных коэффициентов корреляции при незначительных объемах выборочной совокупности.
говорит лишь об отсутствии линейной корреляционной зависимости, но не вообще об отсутствии корреляционной, а тем более статистической зависимости. Величина коэффициента корреляции не является доказательством наличия причинно-следственной связи между исследуемыми признаками, а является оценкой степени взаимной согласованности в изменениях признаков. Установлению причинно-следственной зависимости предшествует анализ качественной природы явлений. Особенно осторожно следует подходить к истолкованию полученных коэффициентов корреляции при незначительных объемах выборочной совокупности.
Пусть по результатам выборочного наблюдения 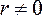 . Объясняется ли это действительно существующей корреляционной связью между признаками
. Объясняется ли это действительно существующей корреляционной связью между признаками 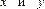 в генеральной совокупности или является следствием случайности отбора элементов в выборку?
в генеральной совокупности или является следствием случайности отбора элементов в выборку?
По вычисленному значению выборочного коэффициента корреляции 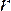 требуется проверить гипотезу
требуется проверить гипотезу
Н0: коэффициент корреляции в генеральной совокупности равен нулю
при альтернативе
Н1: коэффициент корреляции в генеральной совокупности не равен нулю.
В качестве статистического критерия для гипотезы Н0 обычно используется величина
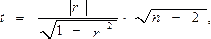
которая распределена по закону Стьюдента с 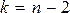 степенями свободы. Гипотеза Н0 отвергается (т.е. зависимость считается установленной), если
степенями свободы. Гипотеза Н0 отвергается (т.е. зависимость считается установленной), если 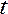 превысит допустимое значение
превысит допустимое значение 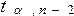 при уровне значимости
при уровне значимости 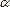 и
и 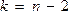 степенями свободы. Некоторые значения критерия приведены ниже в таблице.
степенями свободы. Некоторые значения критерия приведены ниже в таблице.
Таблица 11.
Допустимые значения критерия Стьюдента при числе степеней свободы 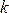 и уровне значимости
и уровне значимости 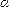 .
.
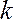 |
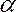 |
|
| 0,05 | 0,01 | |
| 2,10 | 2,88 | |
| 2,09 | 2,86 | |
| 2,09 | 2,85 | |
| 2,08 | 2,83 | |
| 2,07 | 2,82 | |
| 2,07 | 2,81 | |
| 2,06 | 2,80 | |
| 2,06 | 2,79 | |
| 2,06 | 2,78 | |
| 2,05 | 2,77 | |
| 2,05 | 2,76 | |
| 2,05 | 2,76 | |
| 2,04 | 2,75 | |
| 2,02 | 2,70 | |
| 2,00 | 2,66 | |
| 1,98 | 2,62 | |
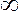 |
1,96 | 2,58 |
Коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае линейной зависимости между признаками. При криволинейной зависимости линейный коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен 0, а потому в таких случаях рекомендуется использовать в качестве показателя степени тесноты связи другие величины. Рассмотрим эмпирическое корреляционное отношение 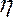 .
.
Согласно правилу сложения дисперсий, общая дисперсия  равна сумме средней из групповых и межгрупповой дисперсий:
равна сумме средней из групповых и межгрупповой дисперсий:
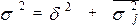 .
.
Первая составляющая - межгрупповая дисперсия 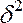 , характеризует ту часть колеблемости результативного признака, которая складывается под влиянием изменения признака-фактора, положенного в основу группировки. Вариацию, обусловленную влиянием прочих факторов, характеризует средняя изгрупповых дисперсий
, характеризует ту часть колеблемости результативного признака, которая складывается под влиянием изменения признака-фактора, положенного в основу группировки. Вариацию, обусловленную влиянием прочих факторов, характеризует средняя изгрупповых дисперсий 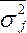 .
.
Зная общую и межгрупповую дисперсии, можно оценить долю, которую составляет вариация под действием фактора 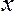 в общей вариации результативного признака
в общей вариации результативного признака 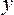 , т.е. найти отношение
, т.е. найти отношение  .
.
Извлекая квадратный корень из этого отношения, получим эмпирическое корреляционное отношение
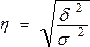 или
или 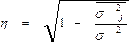
Корреляционное отношение равно нулю, когда нет колеблемости в величине средних значений результативного признака по выделенным группам. В тех случаях, когда средняя из групповых дисперсий близка к нулю, т.е. практически вся вариация результативного признака обусловлена действием фактора 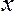 , величина корреляционного отношения близка к 1. Направление связи мы легко установим по данным групповой таблицы (см. пример 9).
, величина корреляционного отношения близка к 1. Направление связи мы легко установим по данным групповой таблицы (см. пример 9).
studopedia.ru
Читайте также
![Сколько значений может принимать дискретная случайная величина Сколько значений может принимать дискретная случайная величина]() Сколько значений может принимать дискретная случайная величина
Сколько значений может принимать дискретная случайная величина![Значения коэффициентов корреляции графиков нагрузки потребителей Значения коэффициентов корреляции графиков нагрузки потребителей]() Значения коэффициентов корреляции графиков нагрузки потребителей
Значения коэффициентов корреляции графиков нагрузки потребителей![Значение коэффициента корреляции Значение коэффициента корреляции]() Значение коэффициента корреляции
Значение коэффициента корреляции![Бит может принимать значения Бит может принимать значения]() Бит может принимать значения
Бит может принимать значения![Расчет коэффициента детерминации невозможен без значения коэффициента Расчет коэффициента детерминации невозможен без значения коэффициента]() Расчет коэффициента детерминации невозможен без значения коэффициента
Расчет коэффициента детерминации невозможен без значения коэффициента![Коэффициент абсолютной ликвидности нормативное значение Коэффициент абсолютной ликвидности нормативное значение]() Коэффициент абсолютной ликвидности нормативное значение
Коэффициент абсолютной ликвидности нормативное значение![Корреляция значения Корреляция значения]() Корреляция значения
Корреляция значения![Коэффициент концентрации привлеченного капитала нормативное значение Коэффициент концентрации привлеченного капитала нормативное значение]() Коэффициент концентрации привлеченного капитала нормативное значение
Коэффициент концентрации привлеченного капитала нормативное значение![Значением логической переменной может быть Значением логической переменной может быть]() Значением логической переменной может быть
Значением логической переменной может быть![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского- 7 Треф значение
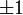 тогда и только тогда, когда X и Y линейно зависимы:
тогда и только тогда, когда X и Y линейно зависимы: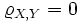 . Обратное в общем случае неверно.
. Обратное в общем случае неверно.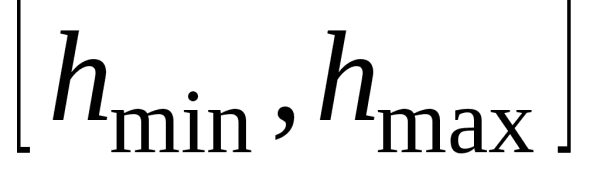 Сколько значений может принимать дискретная случайная величина
Сколько значений может принимать дискретная случайная величина Значения коэффициентов корреляции графиков нагрузки потребителей
Значения коэффициентов корреляции графиков нагрузки потребителей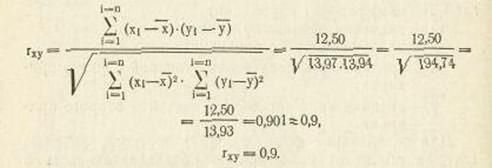 Значение коэффициента корреляции
Значение коэффициента корреляции Бит может принимать значения
Бит может принимать значения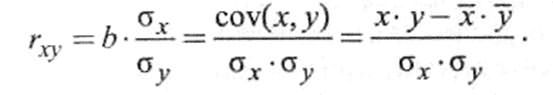 Расчет коэффициента детерминации невозможен без значения коэффициента
Расчет коэффициента детерминации невозможен без значения коэффициента Коэффициент абсолютной ликвидности нормативное значение
Коэффициент абсолютной ликвидности нормативное значение Корреляция значения
Корреляция значения Коэффициент концентрации привлеченного капитала нормативное значение
Коэффициент концентрации привлеченного капитала нормативное значение Значением логической переменной может быть
Значением логической переменной может быть Аутентичность значение слова
Аутентичность значение слова Чувак значение слова с еврейского
Чувак значение слова с еврейского