Среднее значение
Сре́днее значе́ние — числовая характеристика множества чисел или функций (в математике); — некоторое число, заключённое между наименьшим и наибольшим из их значений.
Основные сведения
Исходным пунктом становления теории средних величин явилось исследование пропорций школой Пифагора. При этом не проводилось строгого различия между понятиями средней величины и пропорции. Значительный толчок развитию теории пропорций с арифметической точки зрения был дан греческими математиками — Никомахом Герасским (конец I — начало II в. н. э.) и Паппом Александрийским (III в. н. э.). Первым этапом развития понятия средней является этап, когда средняя стала считаться центральным членом непрерывной пропорции. Но понятие средней как центрального значения прогрессии не даёт возможности вывести понятие средней по отношению к последовательности n членов, независимо от того, в каком порядке они следуют друг за другом. Для этой цели необходимо прибегнуть к формальному обобщению средних. Следующий этап — переход от непрерывных пропорций к прогрессиям — арифметической, геометрической и гармонической (англ.)[1].
В истории статистики впервые широкое употребление средних величин связано с именем английского учёного У. Петти. У. Петти один из первых пытался придать средней величине статистический смысл, связав её с экономическими категориями. Но описания понятия средней величины, его выделения, Петти не произвёл. Родоначальником теории средних величин принято считать А. Кетле. Он одним из первых начал последовательно разрабатывать теорию средних величин, пытаясь подвести под неё математическую базу. А. Кетле выделял два вида средних величин — собственно средние и средние арифметические. Собственно средние представляют вещь, число, действительно существующие. Собственно средние или средние статистические должны выводиться из явлений однокачественных, одинаковых по своему внутреннему значению. Средние арифметические — числа, дающие возможно близкое представление о многих числах, различных, хотя и однородных[2].
Каждый из видов средней может выступать либо в форме простой, либо в форме взвешенной средней. Правильность выбора формы средней вытекает из материальной природы объекта исследования. Формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются. Когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторений индивидуальных значений признака присутствует в расчётных формулах степенных средних. В этом случае они называются формулами взвешенных средних.[3]
Иерархия средних значений в математике
- среднее значение функции — понятие, определяемое многими способами.
- Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
- среднее степенное — частный случай средних Колмогорова при ϕ ( x ) = x α {\displaystyle \phi (x)=x^{\alpha }} . Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
- среднее арифметическое ( α = 1 {\displaystyle \alpha =1} );
- среднее квадратическое ( α = 2 {\displaystyle \alpha =2} );
- среднее гармоническое ( α = − 1 {\displaystyle \alpha =-1} );
- по непрерывности при α → 0 {\displaystyle \alpha \to 0} доопределяется среднее геометрическое, которое также является Колмогоровским средним при ϕ ( x ) = log x {\displaystyle \phi (x)=\log x}
- среднее степенное — частный случай средних Колмогорова при ϕ ( x ) = x α {\displaystyle \phi (x)=x^{\alpha }} . Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
- Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
- Среднее взвешенное — обобщение средней величины на случай произвольной линейной комбинации:
- Среднее арифметическое взвешенное.
- Среднее геометрическое взвешенное.
- Среднее гармоническое взвешенное.
- среднее хронологическое — обобщает значения признака для одной и той же единицы или совокупности в целом, изменяющихся во времени.
- среднее логарифмическое, определяемое по формуле a ¯ = a 1 − a 2 ln ( a 1 / a 2 ) {\textstyle {\bar {a}}={\frac {a_{1}-a_{2}}{\ln(a_{1}/a_{2})}}} , используется в теплотехнике
- среднее логарифмическое, определяемое в электроизоляции соответствии с ГОСТ 27905.4-88 определяется как l o g a ¯ = log a 1 + l o g a 2 + . . . + . . . l o g a n a 1 + a 2 + . . . + a n {\textstyle log{\bar {a}}={\frac {\log a_{1}+loga_{2}+...+...loga_{n}}{a_{1}+a_{2}+...+a_{n}}}} (логарифм по любому основанию)[4]
В теории вероятностей и статистике
Основная статья: Показатели центра распределения- непараметрические средние — мода, медиана.
- среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.
ru.wikipedia.org
СРЕДНЕЕ ЗНАЧЕНИЕ это:
СРЕДНЕЕ ЗНАЧЕНИЕ СРЕДНЕЕ ЗНАЧЕНИЕ (average) Статистический обобщенный показатель какой-либо величины. Среднее ряда чисел может быть взвешенным или невзвешенным. Невзвешенное среднее значение, или среднее арифметическое, N чисел x1, x2,..., xN равно их сумме, деленной на N, и записывается как (eixi)/N. При расчете невзвешенного среднего значения каждое число имеет одинаковый вес; этот показатель часто бывает полезен, когда данные относятся к характеристикам людей. При расчете взвешенного среднего каждое наблюдение (значение) имеет свой вес, обозначаемый wi; таким образом, среднее взвешенное равно сумме результатов наблюдений и их весов, (xiwi), деленной на сумму весов, и записывается как (eixiwi)/(eiwi)Например, среднее взвешенное более точно отражает средний доход населения Латинской Америки. В Бразилии проживает гораздо больше людей, чем в Уругвае, поэтому если хi – средний доход в каждой из стран, то наиболее подходящими весами wi будет численность населения в соответствующих странах.Экономика. Толковый словарь. — М.: "ИНФРА-М", Издательство "Весь Мир". Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М.. 2000.
Экономический словарь. 2000.
dic.academic.ru
Среднее арифметическое
У этого термина существуют и другие значения, см. среднее значение.Сре́днее арифмети́ческое (в математике и статистике) множества чисел — сумма всех чисел, делённая на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ {\displaystyle {\bar {x}}} , произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и x ¯ {\displaystyle {\bar {x}}} в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда x ¯ {\displaystyle {\bar {x}}} (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + ⋯ + x n ) . {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n}).}Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры
- Для трёх чисел необходимо сложить их и разделить на 3:
- Для четырёх чисел необходимо сложить их и разделить на 4:
Или проще 5+5=10, 10:2. Потому что мы складывали 2 числа, а значит, сколько чисел складываем, на столько и делим.
Непрерывная случайная величина
Для непрерывно распределённой величины f ( x ) {\displaystyle f(x)} среднее арифметическое на отрезке [ a ; b ] {\displaystyle [a;b]} определяется через определённый интеграл:
f ( x ) ¯ [ a ; b ] = 1 b − a ∫ a b f ( x ) d x {\displaystyle {\overline {f(x)}}_{[a;b]}={\frac {1}{b-a}}\int _{a}^{b}f(x)dx}Некоторые проблемы применения среднего
Отсутствие робастности
Основная статья: Робастность в статистикеХотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Основная статья: Окупаемость инвестицийЕсли числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года всего на $5.1, средний рост в 8,2 % даёт конечный результат $35.1:
[$30 (1 — 0.1) (1 + 0.3) = $30 (1 + 0.082) (1 + 0.082) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: [$30 (1 + 0.1) (1 + 0.1) = $36.3].
Сложный процент в конце 2 года: 90 % * 130 % = 117 % , то есть общий прирост 17 %, а среднегодовой сложный процент 117 % ≈ 108.2 % {\displaystyle {\sqrt {117\%}}\approx 108.2\%} , то есть среднегодовой прирост 8,2 %.
Направления
Основная статья: Статистика направленийПри расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 1 ∘ + 359 ∘ 2 = {\displaystyle {\frac {1^{\circ }+359^{\circ }}{2}}=} 180°. Это число неверно по двум причинам.
- Во-первых, угловые меры определены только для диапазона от 0° до 360° (или от 0 до 2π при измерении в радианах). Таким образом, ту же пару чисел можно было бы записать как (1° и −1°) или как (1° и 719°). Средние значения каждой из пар будут отличаться: 1 ∘ + ( − 1 ∘ ) 2 = 0 ∘ {\displaystyle {\frac {1^{\circ }+(-1^{\circ })}{2}}=0^{\circ }} , 1 ∘ + 719 ∘ 2 = 360 ∘ {\displaystyle {\frac {1^{\circ }+719^{\circ }}{2}}=360^{\circ }} .
- Во-вторых, в данном случае, значение 0° (эквивалентное 360°) будет геометрически лучшим средним значеним, так как числа отклоняются от 0° меньше, чем от какого-либо другого значения (у значения 0° наименьшая дисперсия). Сравните:
- число 1° отклоняется от 0° всего на 1°;
- число 1° отклоняется от вычисленного среднего, равного 180°, на 179°.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
ru.wikipedia.org
Средние величины.
Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина, представляющая собойобобщенную количественную характеристику признания в статистической совокупности в конкретных условиях места и времени.
Средняя величина выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из выражающих признаков.
Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Средняя величина будет типичной только тогда, когда она будет рассчитана по качественно однородной совокупности.
Например используя для расчета средние величины доходов: служащих государственных, совместных предприятий, наука, культура и т.п., является крайне неоднородной.
В этом и других случаях метод средних используется в сочетании с методом группировок: если совокупность не однородна – общее среднее должны быть занесены или дополнены групповыми средними, т.е. средними, рассчитанными по по качественно однородным группам.
Виды средних и методы их расчета.
В практике статистической обработки материала возникают различные задачи, имеются особенности изучаемых явлений и поэтому для их решения требуются различные средние.
Математическая статистика выводит различные средние из формул степенной средней:
![]() =
=![]()
![]() =
=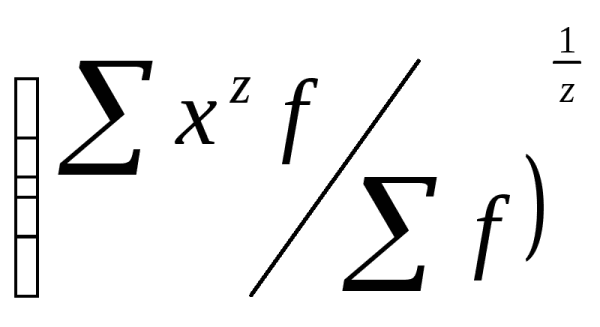
При Z = 1 ср. арифметическая
Z = 0 ср. геометрическая
Z =-1 ср. гармоническая
Z =2 ср. квадратическая
Однако вопрос о том, какой вид средней необходимо применить в отдельном случае, разрешается путем конкретного анализа изучаемой совокупности введем следующие понятия:
1 признак по которому находится средняя называется осредняемым признаком (![]() )
)
2 величина осредняемого признака у каждой единицы совокупности называется индивидуальным значением осредняемого признака или вариантами (х; х2; х3….хn)
3 Чаcтота – это повторяемость индивидуальных значений признака (f)
Средняя арифметическая – распространенная. Она исчисляется в тех случаях, когда объем определяемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.
В зависимости от характера исходных данных средняя арифметическая определяется следующим образом:
1 Н-р Найти средний стаж работы 10 работников: 6,5,4,3,3,4,5,4,5,4, т.е. даны одиночные значения
![]() =
= ![]() =(6+5+4+3+3+4+5+4+5+4)/10 = 43/10 = 4,3года
=(6+5+4+3+3+4+5+4+5+4)/10 = 43/10 = 4,3года
-
Когда значение признака встречается несколько раз.
Средня взвешенная арифметическая
![]() =
= ![]() или
или ![]() =
= ![]()
![]()
Пример расчета
|
Взвешенная дискретная |
Взвешенная интервальная |
|||
|
Оценки, получаемые на экзамене по математике |
Число неявок на занятия |
|||
|
оценки |
Кол-во студентов |
Группы по числу неявок |
Число студентов |
|
|
2 3 4 5 |
1 2 10 7 |
интервальный |
дискретный |
|
|
До5 6-10 11-15 16-20 >20 |
8-5=3 8 5 3 1 |
3 8 5 3 1 |
||
|
Итого: |
20 |
Итого: |
20 |
|
![]() = (2*1+3*2+4*10+5*7)/20=83/20 = 4.15
= (2*1+3*2+4*10+5*7)/20=83/20 = 4.15
![]() =3*3+8*8+13*5+18*3+23/20 = 215/20=10.75
=3*3+8*8+13*5+18*3+23/20 = 215/20=10.75
Свойства средней арифметической
П-р Продажа акций АО «Дока хлеб» на торгах фондовой секции ТБМ «Гермес»
|
Сумма |
Кол-во проданных акций, шт. |
Курс продажи, руб. |
|
1 |
500 |
1080 |
|
2 |
300 |
1050 |
|
3 |
1100 |
1145 |
1 средняя арифметическая из постоянных чисел равна этому постоянному числу
Если х = а. Тогда ![]() =
=![]()
2 Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно Ито же число, то ![]() нового ряда от этого не изменится.
нового ряда от этого не изменится.
Уменьшатся все f в к раз.
![]() =
=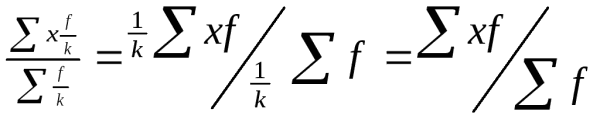
![]() = 1112.89=1112.9
= 1112.89=1112.9
-
Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна 0, т.е.
![]()
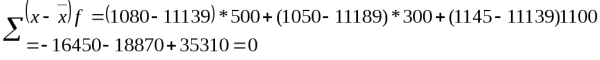
из-за округления.
4 Если все варианты уменьшить или увеличить на какое- либо число, то среднее арифметическое нового ряда уменьшится или увеличится на столько же.
X1 = x-a
![]()
Курс продажи увеличился в 1,5 раза, т.е. на 50%
![]()
5Если все варианты уменьшить или увеличить в к раз, то среднее арифметическое нового ряда уменьшится или увеличится во столько же, т.е. в к раз
Пусть ![]()
Отсюда ![]() в полтора раза
в полтора раза
![]()
иногда роль частот при исчислении средней играет частота (w) . Посчитаем частоты во втором примере
W, % 15; 40; 25; 15; 5;
![]()
Средняя гармоническая.
Это величина обратная средней арифметической, когда z=-1.
Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется средне гармоническая взвешенная.
Н-р, расчет средней цены
Средняя цена = ![]()
|
Город |
Цена, руб. хi |
|
Частоты
|
|
А |
30 |
600 |
20 |
|
Б |
20 |
1000 |
50 |
|
В |
35 |
350 |
10 |
|
Итого: |
1950 |
80 |
Известны:
1 ![]() реализации
реализации
2 Цена Найти: Кол-во реализованных единиц.
![]()
![]()
Неверный путь.
![]()
![]()
![]()
простая ![]()
Где ![]() - сумма обратных значений вариант
- сумма обратных значений вариант
n – число вариант M=fx
Применение: для расчета некоторых индексов, в частности индекса цен.
Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии Z=0 ![]()
т![]() .е. прямой подставленной средняя не выводится.n – число вариант
.е. прямой подставленной средняя не выводится.n – число вариант
Пример
Доходы населения России представлены табл.
|
1985г. |
244,7 млрд. |
|
1986г |
283,6 млрд. |
|
1987г |
264,3 млрд. |
|
1988г |
287,2 млрд. |
|
1989г |
324,6 млрд. |
|
1990 г |
384,7 млрд. |
Рассчитать средне годовой доход населения
Решение
1 найдем цепные Тр
1985г
1986г 253,6/244,7 =1,04
1987г 264,3/253,6 =1,04
1988г 1,09
1989г 1,13
1990г 1,18
![]()
Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношением двух чисел. Поэтому ср. геометрическая используется в расчетах ср. годовых темпов роста.
![]() простая
простая
![]() взвешенная
взвешенная
где х – вариант осредняемого критерия
П – произведение вариантов
f – частота вариантов
Средняя квадратичная.
Z=2
![]() =
=![]()
В экономических исследованиях ср. квад. в измененном виде широко используется для характеристики вариации признака (дисперсия, среднее квадратическое отклонение).
Между степенными средними существует следующая зависимость: чем больше показатель степени, тем > значение средней.
|
Значение к |
-1 |
0 |
1 |
2 |
и т.д. |
|
Отношение м\у сред |
|
|
|
|
и т.д. |
Соотношение это называется правилом мажорантности.
Формула ср. арифметической взвешенной
![]()
![]() m1i+A , где m1=
m1i+A , где m1= ![]()
Средняя m1 из значений ![]()
![]() называется моментом 1 порядка, а способ вычисления средней – способом моментов. Иногда его называют способом отсчета от условного нуля.
называется моментом 1 порядка, а способ вычисления средней – способом моментов. Иногда его называют способом отсчета от условного нуля.
Расчет среднего арифметического способом « условного нуля ».
|
Валовая продукция, млн. руб |
Число пред, % |
Середина шт. ед. х |
х - 225 |
|
|
|
До 50 |
3 |
25 |
-200 |
-4 |
-12 |
|
50-100 |
6 |
75 |
-150 |
-3 |
-18 |
|
100-150 |
10 |
125 |
-100 |
-2 |
-20 |
|
150-200 |
21 |
175 |
-50 |
-1 |
-21 |
|
200-250 |
33 |
225 |
0 |
0 |
0 |
|
250-300 |
18 |
275 |
50 |
1 |
18 |
|
Более 300 |
9 |
325 |
100 |
2 |
18 |
|
итого |
100 |
- |
- |
- |
-35 |
![]()
Пример на решение задачи с применением свойств средней.
|
х |
f |
x*100 |
х*100-48 |
f |
f*х/ |
|
0,13 |
200 |
13 |
-35 |
2 |
-70 |
|
0,28 |
250 |
28 |
-20 |
2,5 |
-50 |
|
0,33 |
300 |
33 |
-15 |
3 |
-45 |
|
0,48 |
350 |
48 |
0 |
3,5 |
0 |
|
0,53 |
300 |
53 |
+5 |
3 |
15 |
|
0,68 |
200 |
68 |
20 |
2 |
40 |
|
итого |
1600 |
16 |
-110 |
Свойство 1. При увеличении х в 100 раз средняя арифметическая увеличивается в 100 раз.
Свойство 2. Правило условного нуля.
Свойство 3.При уменьшении f в 100 раз средняя не меняется.
![]()
![]()
Структурные средние величины.
Для характеристики структуры совокупности применяются особые показатели, которые можно назвать структурными средними. К таким показателям относятся мода и медиана.
Модой (Мо) называется чаще всего встречающийся вариант, или модой называется то значение признака, которое соответствует max точке теоретической кривой распределения.
|
Для дискретных рядов |
Для интервальных рядов |
||||||
|
Размер обуви |
Число купленных пар |
f |
Стаж(лет) |
Число работников |
F/ |
||
|
34 35 36 37 38 39 40 |
2 10 20 88 19 9 2 |
2 12 32 120 139 148 |
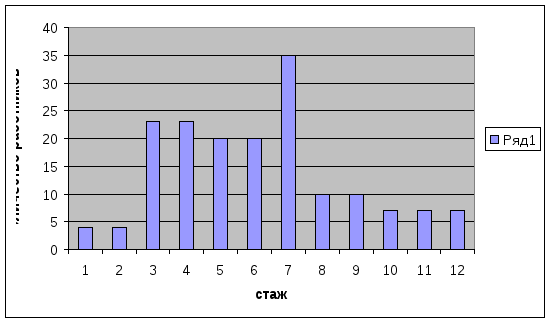
До 2 2-4 4-6 6-8 8-10 свыше 10 |
4 23 20 35 11 7 |
4 27 47 82 93 100 |
||
|
итого |
150 |
итого |
100 |
||||
Мо- это варианта с наибольшей частотой Мо= 37,т.к. fmax =88
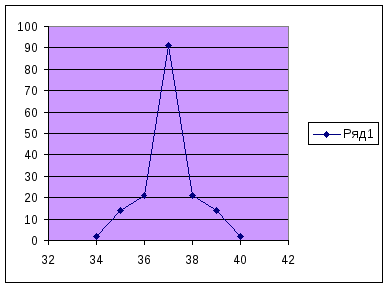
Мо приближенно считают центральный вариант модального интервала, т.е., того интервала, который имеет наибольшую частоту (частость). В пределах интервала когда найти то значение признака, который является модой.
Если распределение симметрично, то в качестве моды будет середина модального интервала, ото в том случае, если соседние с модальными, мало отличаются друг от друга. В ряду может использовано мод. Наикратное значение моды для интервального ряда.
Мо= Хмо+ hмо (f мо- fмо-1)
(fмо-fмо-1)+(fмо-fмо-1)
Хо+К* f2-f1
(f2-f1)(f2-f3)
Где хмо - нижняя граница модального интервала
hмо - величина модального интервала
fмо -частота модального интервала
fмо-1 – частота предшествующая модальному интервалу
fмо+1-частота , интервала, следующегоза модальным.
Модальный интервал от 6-8
Мо= 6+2 35-20 6+ 30
35-20+35-11 = 39 = 6+0,77=6,77года
Мо применяется:
1 при изучении цен на рынках
2 при изучении спроса населения на определенный товар т.е. мода характеризует типичность.
Медиана.
Ме называется значение признака у средней единицы ранжированного ряда
Ранжированный ряд -это ряд, у которого значения признака записаны в порядке возрастания или убывания.
Что бы найти Ме определяется:
1 Порядковый № сумма f четное, то ![]() ; еслиn-нечетное , то
; еслиn-нечетное , то ![]()
2 по накопленной частоте определяем ее значение.
|
Дискретный ряд |
Интервальный |
|
Ме определяется по накопленной частоте и номеру Ме.
накопленная частота 120 показывает, что купленных пар не привышают 37 размер, а 32, что 32 пары. => 75 пара будет 37р. |
где Ме – нужная граница медианного интервала h- величина медианного интервала
fме-1- частота (частость) наполненная до медианного интервала . fме – частота(частость)медианного интервала. |
![]()
![]()
Ме находит практическое применение вследствие особого свойства ![]() абсолютных отклонений членов ряда от Ме есть величина наименьшая
абсолютных отклонений членов ряда от Ме есть величина наименьшая
![]()
Ме находит широкое практическое применение в маркетинговой деятельности.
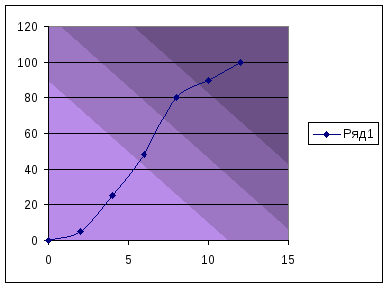
Величины, приходящиеся на ¼ и ¾ расстояния от начала ряда называется нижний квартиль, а ¾ и ¼ верхний квартиль.
Т.е. квартиль это варианты, делящие ряд на 4 равные части.
Дециль- варианты, делящие ранжированный ряд на 10 равных частей
1 дециль 1/10 к 9/10
2 дециль2/10 к 8/10 и т.д.
процентиль – на 100 равных частей.
Соотношение между ![]() , Мо и Ме.
, Мо и Ме.
1 Если ![]() = Мо = Ме, то распределение симметрично, т.е. группа симметрична.
= Мо = Ме, то распределение симметрично, т.е. группа симметрична.
2 Ме <
![]() при небольшой группе с большими числами.
при небольшой группе с большими числами.
3 ![]() < Ме при большой концентрации данных и не очень больших числах.
< Ме при большой концентрации данных и не очень больших числах.
4 Мо <
![]() , если совокупность неоднородна
, если совокупность неоднородна
5 Мо > ![]() , если совокупность небольшая и Мо отчетливо выражена.
, если совокупность небольшая и Мо отчетливо выражена.
Все рассмотренные формы степенной средней обладают важным свойством(в отличие от структурных средних)- в формулу определения средней входят все значения ряда т.е. на размеры средней оказывают влияние значение каждого варианта.
С одной стороны, это весьма положительное свойство т.к. в этом случае учитывается действие всех причин воздействующих на все единицы изучаемой совокупности.
С другой стороны, даже одно наблюдение попавшее в исходные данные случайно может существенным образом исказить представление об уровне развития изучаемого признака в рассматриваемой совокупности.
Особенно большое значение это имеет для коротких рядов.
StudFiles.ru
Среднее значение функции
У этого термина существуют и другие значения, см. среднее значение.Среднее значение функции — это некоторое число, заключённое между наименьшим и наибольшим её значениями. В дифференциальном и интегральном исчислении имеется ряд «теорем о среднем», устанавливающих существование таких точек, в которых функция или её производная получает то или иное среднее значение. Наиболее важной теоремой о среднем значении функции в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если f ( x ) {\displaystyle f(x)} непрерывна на отрезке [ a , b ] {\displaystyle [a,b]} и дифференцируема в интервале ( a , b ) {\displaystyle (a,b)} , то существует точка c {\displaystyle c} , принадлежащая интервалу ( a , b ) {\displaystyle (a,b)} , такая, что f ( b ) − f ( a ) = ( b − a ) f ′ ( c ) {\displaystyle f(b)-f(a)=(b-a)f'(c)} . В интегральном исчислении наиболее важной теоремой о среднем значении является следующая: если f ( x ) {\displaystyle f(x)} непрерывна на отрезке [ a , b ] {\displaystyle [a,b]} , а φ ( x ) {\displaystyle \varphi (x)} сохраняет постоянный знак, то существует точка c {\displaystyle c} из интервала ( a , b ) {\displaystyle (a,b)} такая, что
∫ a b f ( x ) φ ( x ) d x = f ( c ) ∫ a b φ ( x ) d x . {\displaystyle \int \limits _{a}^{b}f(x)\varphi (x)dx=f(c)\int \limits _{a}^{b}\varphi (x)dx.}В частности, если φ ( x ) = 1 {\displaystyle \varphi (x)=1} , то
∫ a b f ( x ) d x = f ( c ) ( b − a ) . {\displaystyle \int \limits _{a}^{b}f(x)dx=f(c)(b-a).}Вследствие этого под средним значением функции f ( x ) {\displaystyle f(x)} на отрезке [ a , b ] {\displaystyle [a,b]} обычно понимают величину
f ¯ = 1 b − a ∫ a b f ( x ) d x . {\displaystyle {\overline {f}}={\frac {1}{b-a}}\int \limits _{a}^{b}f(x)dx.}Аналогично определяется среднее значение функции нескольких переменных в некоторой области.
ru.wikipedia.org
Читайте также
![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![1515 На часах значение 1515 На часах значение]() 1515 На часах значение
1515 На часах значение![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия![16 16 Значение времени 16 16 Значение времени]() 16 16 Значение времени
16 16 Значение времени![15 15 Значение 15 15 Значение]() 15 15 Значение
15 15 Значение![Безопасное значение темпа роста прибыли должно быть Безопасное значение темпа роста прибыли должно быть]() Безопасное значение темпа роста прибыли должно быть
Безопасное значение темпа роста прибыли должно быть![Аарон значение имени Аарон значение имени]() Аарон значение имени
Аарон значение имени![Язык без костей значение фразеологизма Язык без костей значение фразеологизма]() Язык без костей значение фразеологизма
Язык без костей значение фразеологизма![2112 На часах значение 2112 На часах значение]() 2112 На часах значение
2112 На часах значение![Агнесса значение имени Агнесса значение имени]() Агнесса значение имени
Агнесса значение имени![Аделина значение имени характер Аделина значение имени характер]() Аделина значение имени характер
Аделина значение имени характер
 Аутентичность значение слова
Аутентичность значение слова 1515 На часах значение
1515 На часах значение Чувак значение слова с еврейского
Чувак значение слова с еврейского Барыга значение слова википедия
Барыга значение слова википедия 16 16 Значение времени
16 16 Значение времени 15 15 Значение
15 15 Значение Безопасное значение темпа роста прибыли должно быть
Безопасное значение темпа роста прибыли должно быть Аарон значение имени
Аарон значение имени Язык без костей значение фразеологизма
Язык без костей значение фразеологизма 2112 На часах значение
2112 На часах значение Агнесса значение имени
Агнесса значение имени Аделина значение имени характер
Аделина значение имени характер