Понятие функции нескольких переменных
Если каждой точке X = (х1, х2, …хn) из множества {X} точек n–мерного пространства ставится в соответствие одно вполне определенное значение переменной величины z, то говорят, что задана функция n переменных z = f(х1, х2, …хn) = f (X).
При этом переменные х1, х2, …хn называют независимыми переменными или аргументами функции, z - зависимой переменной, а символ f обозначает закон соответствия. Множество {X} называют областью определения функции (это некое подмножество n-мерного пространства).
Например, функция z = 1/(х1х2) представляет собой функцию двух переменных. Ее аргументы – переменные х1 и х2, а z – зависимая переменная. Область определения – вся координатная плоскость, за исключением прямых х1 = 0 и х2 = 0, т.е. без осей абсцисс и ординат. Подставив в функцию любую точку из области определения, по закону соответствия получим определенное число. Например, взяв точку (2; 5), т.е. х1 = 2, х2 = 5, получим
z = 1/(2*5) = 0,1 (т.е. z(2; 5) = 0,1).
Функция вида z = а1х1 + а2х2 + … + аnхn + b, где а1, а2,…, аn, b — по стоянные числа, называют линейной. Ее можно рассматривать как сумму n линейных функций от переменных х1, х2, …хn. Все остальные функции называют нелинейными.
Например, функция z = 1/(х1х2) – нелинейная, а функция z =
= х1 + 7х2 - 5 – линейная.
Любой функции z = f (X) = f(х1, х2, …хn) можно поставить в соответствие n функций одной переменной, если зафиксировать значения всех переменных, кроме одной.
Например, функции трех переменных z = 1/(х1х2х3) можно поставить в соответствие три функции одной переменной. Если зафиксировать х2 = а и х3 = b то функция примет вид z = 1/(аbх1); если зафиксировать х1 = а и х3 = b, то она примет вид z = 1/(аbх2); если зафиксировать х1 = а и х2 = b, то она примет вид z = 1/(аbх3). В данном случае все три функции имеют одинаковый вид. Это не всегда так. Например, если для функции двух переменных  зафиксировать х2 = а, то она примет вид z = 5х1а, т.е. степенной функции, а если зафиксировать х1 = а, то она примет вид
зафиксировать х2 = а, то она примет вид z = 5х1а, т.е. степенной функции, а если зафиксировать х1 = а, то она примет вид  , т.е. показательной функции.
, т.е. показательной функции.
Графиком функции двух переменных z = f(x, у) называется множество точек трёхмерного пространства (х, у, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением
z = f (x, у). Этот график представляет собой некоторую поверхность в трехмерном пространстве (например, как на рисунке 5.3).
Можно доказать, что если функция – линейная (т.е. z = ax + by + c), то ее график представляет собой плоскость в трехмерном пространстве. Другие примеры трехмерных графиков рекомендуется изучить самостоятельно по учебнику Кремера (стр. 405-406).
Если переменных больше двух (n переменных), то графикфункции представляет собой множество точек (n+1)-мерного пространства, для которых координата хn+1 вычисляется в соответствии с заданным функциональным законом. Такой график называют гиперповерхностью (для линейной функции – гиперплоскостью), и он также представляет собой научную абстракцию (изобразить его невозможно).

Рисунок 5.3 – График функции двух переменных в трехмерном пространстве
Поверхностью уровня функции n переменных называется множество точек в n–мерном пространстве, таких, что во всех этих точках значение функции одно и то же и равно С. Само число С в этом случае называется уровнем.
Обычно для одной и той же функции можно построить бесконечно много поверхностей уровня (соответствующих различным уровням).
Для функции двух переменных поверхность уровня принимает вид линии уровня.
Например, рассмотрим z = 1/(х1х2). Возьмем С = 10, т.е. 1/(х1х2) = 10. Тогда х2 = 1/(10х1), т.е. на плоскости линия уровня примет вид, представленный на рисунке 5.4 сплошной линией. Взяв другой уровень, например, С = 5, получим линию уровня в виде графика функции х2 = 1/(5х1) (на рисунке 5.4 показана пунктиром).

Рисунок 5.4 - Линии уровня функции z = 1/(х1х2)
Рассмотрим еще один пример. Пусть z = 2х1 + х2. Возьмем С = 2, т.е. 2х1 + х2 = 2. Тогда х2 = 2 - 2х1, т.е. на плоскости линия уровня примет вид прямой, представленный на рисунке 5.5 сплошной линией. Взяв другой уровень, например, С = 4, получим линию уровня в виде прямой х2 = 4 - 2х1 (на рисунке 5.5 показана пунктиром). Линия уровня для 2х1 + х2 = 3 показана на рисунке 5.5 точечной линией.
Легко убедиться, что для линейной функции двух переменных любая линия уровня будет представлять собой прямую на плоскости, причем все линии уровня будут параллельны между собой.

Рисунок 5.5 - Линии уровня функции z = 2х1 + х2
studopedia.ru
Определение функции нескольких переменных
Рассматривая функции одной переменной, мы указывали, что при изучении многих явления приходится встречаться с функциями двух и более независимых переменных. Приведем несколько примеров.
Пример 1. Площадь S прямоугольника со сторонами, длины которых равны х и у, выражается формулой S = ху. Каждой паре значений х и у соответствует определенное значение площади S; S есть функция двух переменных.
Пример 2. Объем V прямоугольного параллелепипеда с ребрами, длины которых равны х, у, z, выражается формулой V= xyz. Здесь V есть функция трех переменных х, у, z.
Пример 3. Дальность R полета снаряды, выпущенного с начальной скоростью v0 из орудия, ствол которого наклонен к горизонту под углом , выражается формулой ![]() (если пренебречь сопротивлением воздуха). Здесьg – ускорение силы тяжести. Для каждой пары значений v0 и эта формула дает определенное значение R, т.е. R является функцией двух переменных v0 и .
(если пренебречь сопротивлением воздуха). Здесьg – ускорение силы тяжести. Для каждой пары значений v0 и эта формула дает определенное значение R, т.е. R является функцией двух переменных v0 и .
Пример 4. ![]() . Здесьи есть функция четырех переменных х, у, z, t.
. Здесьи есть функция четырех переменных х, у, z, t.
Определение 1. Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у из некоторой области их изменения D, соответствует определенное значение величины z, то мы говорим, что z есть функция двух независимых переменных х и у, определенная в области D.
Символически функция двух переменных обозначается так:
z= f(x, y), z = F(x, y) и т.д.
Функция двух переменных может быть задана, например, с помощью таблицы или аналитически – с помощью формулы, как это сделано в рассмотренных выше примерах. На основании формулы можно составить таблицу значений функции для некоторых пар значений независимых переменных. Так, для первого примера можно составить следующую таблицу:
S = ху
|
у |
0 |
1 |
1,5 |
2 |
3 |
|
1 2 3 4 |
0 0 |
1 2 3 4 |
1,5 3 4,5 6 |
2 4 6 8 |
3 6 9 12 |
В этой таблице на пересечении строки и столбца, соответствующих определенным значениям х и у, проставлено соответствующее значение функции S. Если функциональная зависимость z= f(x, y) получается в результате измерений величины z при экспериментальном изучении какого-либо явления, то сразу получается таблица, определяющая z как функцию двух переменных. В этом случае функция задается только таблицей.
Как и в случае одной независимой переменной, функция двух переменных существует, вообще говоря, не при любых значениях х и у.
Определение 2. Совокупность пар (х, у) значений х и у, при которых определяется функция z= f(x, y), называется областью определения или областью существования этой функции.
Область определения функции наглядно иллюстрируется геометрически. Если каждую пару значений х и у мы будем изображать точкой М(х, у) в плоскости Оху, то область определения функции изобразится в виде некоторой совокупности точек на плоскости. Эту совокупность точек будем также называть областью определения функции. В частности, областью определения может быть и вся плоскость. В дальнейшем мы будем главным образом иметь дело с такими областями, которые представляют собой части плоскости, ограниченные линиями. Линию, ограничивающую данную область, будем называть границей области. Точки области, не лежащие на границе, будем называть внутренними точками области. Область, состоящая из одних внутренних точек, называется открытой или незамкнутой. Если же к области относятся и точки границы, то область называется замкнутой. Область называется ограниченной, если существует такая постоянная С, что расстояние любой точки М области от начала координат О меньше С, т.е. |OM| < С.
Пример 5. Определить естественную область определения функции
z = 2х – у.
Аналитическое выражение 2х – у имеет смысл при любых значениях х и у. Следовательно, естественной областью определения функции является вся плоскость Оху.
Пример 6. ![]() .
.
Для того чтобы z имело действительное значение, нужно, чтобы под корнем стояло неотрицательное число, т.е. х и у должны удовлетворять неравенству 1 – х2 – у2 0, или х2 + у2 1.
Все точки М(х, у), координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса 1 с центром в начале координат и на границе этого круга.
Пример 7. ![]() .
.
Так как логарифмы определены только для положительных чисел, то должно удовлетворяться неравенство х + у > 0, или у > х.
Это значит, что областью определения функции z является половина плоскости, расположенная над прямой у = х, не включая самой прямой.
Пример 8. Площадь треугольника S представляет собой функцию основания х и высоты у: S= xy/2.
Областью определения этой функции является область х 0, у 0 (так как основание треугольника и его высота не могут быть ни отрицательны, ни нулем). Заметим, что область определения рассматриваемой функции не совпадает с естественной областью определения того аналитического выражения, с помощью которого задается функция, так как естественной областью определения выражения ху/2 является, очевидно, вся плоскость Оху.
Определение функции двух переменных легко обобщить на случай трех или более переменных.
Определение 3. Если каждой рассматриваемой совокупности значений переменных х, у, z, …, u, t соответствует определенное значение переменной w, то будем называть w функцией независимых переменных х, у, z, …, u, t и писать w= F(х, у, z, …, u, t) или w= f(х, у, z, …, u, t) и т.п.
Так же как и для функции двух переменных, можно говорить об области определения функции трех, четырех и более переменных.
Так, например, для функции трех переменных областью определения является некоторая совокупность троек чисел (х, у, z). Заметим тут же, что каждая тройка чисел задает некоторую точку М(х, у, z) в пространстве Охуz. Следовательно, областью определения функции трех переменных является некоторая совокупность точек пространства.
Аналогично этому можно говорить об области определения функции четырех переменных u= f(x, y, z, t) как о некоторой совокупности четверок чисел (x, y, z, t). Однако область определения функции четырех или большего числа переменных уже не допускает простого геометрического истолкования.
В примере 2 приведена функция трех переменных, определенная при всех значениях х, у, z.
В примере 4 приведена функция четырех переменных.
Пример 9. ![]() .
.
Здесь w – функция четырех переменных х, у, z, и, определенная при значениях переменных, удовлетворяющих соотношению:
![]() .
.
StudFiles.ru
Понятие функции нескольких переменных
Введем понятие функции нескольких переменных.
Определение 1. Пусть каждой точке М из множества точек {М} евклидова пространства Em по какому-либо закону ставится в соответствие некоторое число и из числового множества U. Тогда будем говорить, что на множестве {М} задана функция и =f(M). При этом множества {М} и U называются соответственно областью определения (задания) и областью изменения функции f(M).
Как известно, функция одной переменной у = f(x) изображается на плоскости в виде линии. В случае двух переменных область определения {Мп} функции z = f(x, y) представляет собой некоторое множество точек на координатной плоскости Оху (рис. 8.1). Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Аналогичным образом функция от т переменных
![]()
определенная на множестве {М} евклидова пространства Еm, представляет собой гиперповерхность в евклидовом пространстве Еm+1.

Некоторые виды функций нескольких переменных
Рассмотрим примеры функций нескольких переменных и найдем их области определения.
![]()
Решение. Это поверхность в евклидовом пространстве Е3. Областью определения этой функции является все множество точек плоскости Оху. Область значений этой функции — промежуток [0, ![]() ). Данная функция представляет собой параболоид вращения (рис. 8.2): в вертикальных сечениях этой поверхности плоскостями Oxz и Оуz получаются соответственно параболы z= х2 и z= у2.
). Данная функция представляет собой параболоид вращения (рис. 8.2): в вертикальных сечениях этой поверхности плоскостями Oxz и Оуz получаются соответственно параболы z= х2 и z= у2.

![]()
Решение. Это поверхность в евклидовом пространстве Е3. Область определения данной функции — все множество точек евклидова пространства Е2 или плоскости Оху. Эта функция является так называемым эллиптическим конусом с вершиной в начале координат O(0, 0, 0); приведенная формула суммирует две функции, задающие две его симметричные относительно плоскости Оху части (рис. 8.3):


Приведем теперь наиболее часто встречающиеся в различных приложениях виды функций нескольких переменных.
1. Уравнение вида
![]()
называется общим уравнением плоскости в системе координат Oxyz. Вектор ![]() = (А, В, С) перпендикулярен плоскости (8.4); он называется нормальным вектором этой плоскости. Если известно, что плоскость проходит через некоторую точку M0(x0, y0, z0), то она может быть задана уравнением
= (А, В, С) перпендикулярен плоскости (8.4); он называется нормальным вектором этой плоскости. Если известно, что плоскость проходит через некоторую точку M0(x0, y0, z0), то она может быть задана уравнением
![]()
Например, составить уравнение плоскости с перпендикулярным вектором ![]() = (1, 2, -1), проходящей через точку М0 (2, 1, 1), Согласно формуле (8.5) имеем
= (1, 2, -1), проходящей через точку М0 (2, 1, 1), Согласно формуле (8.5) имеем
![]()
2. Функция Кобба—Дугласа — производственная функция, показывающая объем выпуска продукции Q при затратах капитала К и трудовых ресурсов L. Для случая двух переменных она имеет вид
![]()
где А > 0 — параметр производительности конкретно взятой технологии, 0 < α 1 — доля капитала в доходе.
Линии уровня
Понятие линии уровня широко используется прежде всего в геодезии, картографии, при составлении синоптических карт, а также при описании различных физических полей (температура, давление и пр.).
Определение 2. Линией уровня функции двух переменных z = f(x, y) называется плоская кривая, получаемая при пересечении графика этой функции плоскостью z = С, где С — постоянная величина, параллельной координатной плоскости Оху.
Обычно линии уровня, соответствующие различным значениям постоянной величины С, проецируются на одну плоскость, например на координатную плоскость Оху; тогда их удобно анализировать и с их помощью исследовать сложный характер поверхности, описываемой функцией z = f(x, у).
Таким образом, можно сказать, что линии уровня функции z = f(x, у) — это семейство кривых на координатной плоскости Оху, описываемое уравнениями вида
![]()
Обычно берут арифметическую прогрессию чисел Ci с постоянной разностью h; тогда по взаимному расположению линий уровня можно получить представление о форме поверхности, описываемой функцией z =f(x, у). Там, где функция изменяется быстрее, линии уровня сгущаются, а там, где поверхность пологая, линии уровня располагаются реже (рис. 8.4).

Пример 3. Найти линии уровня функции z = х2+у2—2х—2у.
Решение. Линии уровня данной функции — это семейство кривых на плоскости Оху, описываемое уравнением
![]()
Последнее уравнение описывает семейство окружностей с центром в точке O1(l, 1) радиуса r =![]() . Поверхность вращения (параболоид), описываемая данной функцией, становится "круче" по мере ее удаления от оси, которая дается уравнениями x = 1, у = 1.
. Поверхность вращения (параболоид), описываемая данной функцией, становится "круче" по мере ее удаления от оси, которая дается уравнениями x = 1, у = 1.
StudFiles.ru
Область существования. Линии и поверхности уровня
II. Дифференциальное исчисление
Функций НЕСКОЛЬКИХ переменных
§ 1. Функции нескольких переменных. Основные понятия.
Область существования. Линии и поверхности уровня
Чтобы изобразить на плоском рисунке поверхность, заданную функцией двух переменных  , используют так называемые линии уровня, которые задаются уравнением
, используют так называемые линии уровня, которые задаются уравнением  где
где  . Этот способ заключается в следующем: сначала строят сечения поверхности горизонтальными плоскостями
. Этот способ заключается в следующем: сначала строят сечения поверхности горизонтальными плоскостями  , а затем наносят полученные кривые на плоскость
, а затем наносят полученные кривые на плоскость  . На географических картах таким способом изображают рельеф местности.
. На географических картах таким способом изображают рельеф местности.
Поверхности уровня функции  представляют собой геометрическое место точек пространства, в которых данная функция принимает одно и то же значение
представляют собой геометрическое место точек пространства, в которых данная функция принимает одно и то же значение
 .
.
Определение (Функция многих переменных). Если каждой точке  из множества
из множества  точек
точек  -мерного евклидова пространства
-мерного евклидова пространства  ставится в соответствие по известному закону некоторое число
ставится в соответствие по известному закону некоторое число  то говорят, что на множестве
то говорят, что на множестве  задана функция
задана функция  , или
, или  . При этом множество
. При этом множество  называется областью задания функции
называется областью задания функции 
Число  соответствующее данной точке
соответствующее данной точке  из множества
из множества  , называют частным значением функции в точке
, называют частным значением функции в точке  . Совокупность всех частных значений функции
. Совокупность всех частных значений функции  называют множеством значений этой функции. Так как точка
называют множеством значений этой функции. Так как точка  определяется своими координатами
определяется своими координатами  то для функции
то для функции  переменных
переменных  используется еще одно обозначение
используется еще одно обозначение 
Пример 1.1. Найти область значений функции 
Решение. Областью задания этой функции является круг радиусом 1 с центром в начале координат, а множество значений представляет собой отрезок 
Пример 1.2. Найти область определения функции
 .
.
Решение. Эта функция определена для всех троек  , удовлетворяющих одновременно условиям
, удовлетворяющих одновременно условиям 
Пример 1.3. Найти линии уровня функции  .
.
Решение. На основе определения линий уровня запишем
 , или
, или  . Преобразуем это выражение:
. Преобразуем это выражение:
 .
.
Таким образом, линии уровня заданной функции являются эллип-сами.
Пример 1.4. Найти поверхности уровня функции  .
.
Решение. Запишем уравнение поверхности уровня
 .
.
Преобразуем это уравнение:
 .
.
Тогда поверхностями уровня будет семейство конусов
 .
.
Сделав замену  , получим
, получим
 ,
,
где  .
.
Определить и изобразить области существования следующих функций:
1.1.  . . |
1.2.  . . |
1.3.  .1.3. .1.3.  . . |
1.4.  . . |
1.5.  . . |
1.6.  . . |
Построить линии уровня следующих функций:
1.7.  . . |
|
1.8. а)  ; ; |
б)  ; ; |
в)  ; ; |
г)  . . |
1.9.  . . |
1.10.  . . |
Построить поверхности уровня следующих функций:
1.11.  . . |
1.12.  . . |
Ответы: 1.1. Все точки плоскости вне круга  . 1.2. Кольцо
. 1.2. Кольцо  . 1.3. Пара вертикальных углов
. 1.3. Пара вертикальных углов  . 1.4. Совокупность четырех октантов пространства. 1.5. Открытая пирамида с вершинами в точках
. 1.4. Совокупность четырех октантов пространства. 1.5. Открытая пирамида с вершинами в точках  . 1.6. Внутренность двуполостного гиперболоида
. 1.6. Внутренность двуполостного гиперболоида  . 1.7. Семейство подобных эллипсов. 1.8. а) I и III квадранты при
. 1.7. Семейство подобных эллипсов. 1.8. а) I и III квадранты при  , семейство двухзвенных ломаных линий, звенья которых параллельны осям координат, а вершины расположены на прямой
, семейство двухзвенных ломаных линий, звенья которых параллельны осям координат, а вершины расположены на прямой  при
при  ; б) линии уровня – стороны углов, параллельные положительным направлениям координатных осей
; б) линии уровня – стороны углов, параллельные положительным направлениям координатных осей  и
и  , с вершинами на прямой
, с вершинами на прямой  ; в) семейство контуров квадратов с общим центром
; в) семейство контуров квадратов с общим центром  , стороны которых параллельны осям координат
, стороны которых параллельны осям координат  и
и  при
при  , точка
, точка  при
при  ; г) прямые, параллельные оси
; г) прямые, параллельные оси  , если
, если  , стороны углов, параллельные координатной оси
, стороны углов, параллельные координатной оси  и положительной полуоси
и положительной полуоси  , с вершинами на параболе
, с вершинами на параболе  , если
, если  , положительная полуось
, положительная полуось  , если
, если  . 1.9. Пучок окружностей, проходящих через начало координат (не включая этого начала) и ортогональных к оси
. 1.9. Пучок окружностей, проходящих через начало координат (не включая этого начала) и ортогональных к оси  . 1.10. Семейство окружностей, ортогональных к оси
. 1.10. Семейство окружностей, ортогональных к оси  и проходящих через точки
и проходящих через точки  , за вычетом последних. 1.11. Семейство двуполостных гиперболоидов при
, за вычетом последних. 1.11. Семейство двуполостных гиперболоидов при  , семейство однополостных гиперболоидов при
, семейство однополостных гиперболоидов при  , конус при
, конус при  . 1.12. Семейство концентрических сфер
. 1.12. Семейство концентрических сфер  при
при  , семейство сферических слоев
, семейство сферических слоев  , где
, где  , при
, при  или
или  .
.
studopedia.ru
Читайте также
- Как найти область определения функции
![Как обозначается область определения функции Как обозначается область определения функции]() Как обозначается область определения функции
Как обозначается область определения функции![Уровень образования это определение Уровень образования это определение]() Уровень образования это определение
Уровень образования это определение![Определение обратной функции Определение обратной функции]() Определение обратной функции
Определение обратной функции![Определение уровня существенности происходит на этапе Определение уровня существенности происходит на этапе]() Определение уровня существенности происходит на этапе
Определение уровня существенности происходит на этапе![Определение уровня существенности в аудите пример Определение уровня существенности в аудите пример]() Определение уровня существенности в аудите пример
Определение уровня существенности в аудите пример![Как найти область значения функции Как найти область значения функции]() Как найти область значения функции
Как найти область значения функции![Акт определение Акт определение]() Акт определение
Акт определение- Актив определение
![База данных определение База данных определение]() База данных определение
База данных определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Власть определение Власть определение]() Власть определение
Власть определение
 x
x Как обозначается область определения функции
Как обозначается область определения функции Уровень образования это определение
Уровень образования это определение Определение обратной функции
Определение обратной функции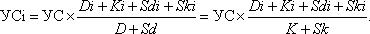 Определение уровня существенности происходит на этапе
Определение уровня существенности происходит на этапе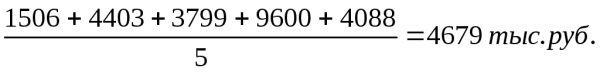 Определение уровня существенности в аудите пример
Определение уровня существенности в аудите пример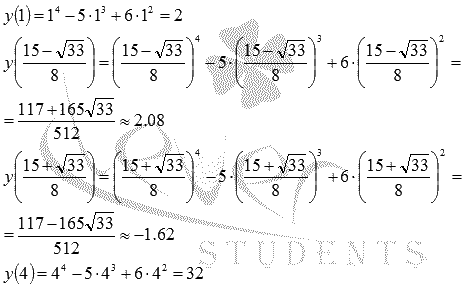 Как найти область значения функции
Как найти область значения функции Акт определение
Акт определение База данных определение
База данных определение Болезнь определение
Болезнь определение Власть определение
Власть определение