Среднее арифметическое
Сущность и значение средних величин.
Абсолютные и относительные величины.
Виды группировок.
В зависимости от задач, решаемых с помощью группировок выделяют следующие их виды:
- типологические
- структурные
- аналитические
Главная задача типологической состоит в классификации социально-экономических явлений путем выделения однородных к качественным отношениям групп.
Качественная однородность при этом понимается в том смысле, что в отношении изучаемого свойства все единицы совокупности подчиняются одному закону развития. Например: группировка предприятиям отраслей экономики.
Абсолютной величиной называется показатель, выражающий размеры социально-экономического явления.
Относительной величиной в статистике называется показатель, выражающий количественное соотношение между явлениями. Он получается в результате деления одной абсолютной величины на другую абсолютную величину. Величина с которой мы производим сравнения называется основанием или базой сравнения.
Абсолютные величины - всегда величины именованные.
Относительные величины выражаются в коэффициентах, процентах, промили и т.д.
Относительная величина показывает, во сколько раз, или на сколько процентов сравниваемая величина больше или меньше базы сравнения.
В статистике различают 8 видов относительных величин:
Средние величины являются одними из наиболее распространенных обобщающих статистических показателей. Они имеют своей целью одним числом охарактеризовать статистическую совокупность состоящую из меньшинства единиц. Средние величины тесно связаны с законом больших чисел. Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.
С помощью метода средних решаются следующие основные задачи:
1. Характеристика уровня развития явлений.
2. Сравнение двух или нескольких уровней.
3. Изучение взаимосвязей социально-экономических явлений.
4. Анализ размещения социально-экономических явлений в пространстве.
Для решения этих задач статистическая методология разработала различные виды средних.
Для выяснения методики расчета средней арифметической используем следующие обозначения:
X - арифметический признак
X (X1, X2, ... X3) - варианты определенного признака
n - число единиц совокупности
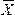 - средняя величина признака
- средняя величина признака
В зависимости от исходных данных средняя арифметическая может быть рассчитана двумя способами:
1. Если данные статистического наблюдения на сгруппированы, или сгруппированные варианты имеют одинаковые частоты, то рассчитывается средняя арифметическая простая:
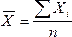
2. Если частоты сгруппированы в данных разные, то рассчитывается среднее арифметическое взвешанное:
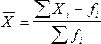
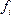 - численность (частоты) вариантов
- численность (частоты) вариантов
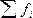 - сумма частот
- сумма частот
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Рассмотрим пример вычисления средней арифметической в дискретном ряду:
| Заработная плата, руб. Xi | Число сотрудников, чел. fi | Произведение вариант на веса (частоты) Xi*fi |
| Итого: |
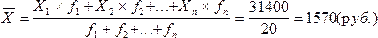
В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному.
В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.
Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.
Если веса fi заданы не в абсолютных показателях, а в относительных, то формула расчета средней арифметической будет следующей:
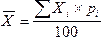
pi - относительные величины структуры, показывающие, какой процент составляют частоты вариантов в сумме всех частот.
Если относительные величины структуры заданы не в процентах, а в долях, то среднее арифметическое будет рассчитываться по формуле:
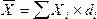
studopedia.ru
Среднеквадратическое отклонение
Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок.
Может обозначаться значком σ (сигма).
Основные сведения
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины.
На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.
Стандартное отклонение на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[1]):
S = 1 n ∑ i = 1 n ( x i − x ¯ ) 2 . {\displaystyle S={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.}Стандартное отклонение на основании несмещённой оценки дисперсии (подправленная выборочная дисперсия[1], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):
S 0 = n n − 1 S 2 = 1 n − 1 ∑ i = 1 n ( x i − x ¯ ) 2 ; {\displaystyle S_{0}={\sqrt {{\frac {n}{n-1}}S^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}};}где S 2 {\displaystyle S^{2}} — выборочная дисперсия; x i {\displaystyle x_{i}} — i-й элемент выборки; n {\displaystyle n} — объём выборки; x ¯ {\displaystyle {\bar {x}}} — среднее арифметическое выборки (выборочное среднее):
x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + … + x n ) . {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).}Само по себе, однако, S 0 {\displaystyle S_{0}} не является несмещённой оценкой квадратного корня из дисперсии, т. е. извлечение квадратного корня «портит» несмещённость.
Обе оценки являются состоятельными[1].
В более общем случае среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[2]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии.
Правило трёх сигм
 График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.
График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.
Правило трёх сигм ( 3 σ {\displaystyle 3\sigma } ) — практически все значения нормально распределённой случайной величины лежат в интервале ( x ¯ − 3 σ ; x ¯ + 3 σ ) {\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)} . Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x ¯ {\displaystyle {\bar {x}}} истинная, а не полученная в результате обработки выборки).
Интерпретация величины среднеквадратического отклонения
Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Практическое применение
На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.
Экономика и финансы
Среднее квадратическое отклонение доходности портфеля σ = D [ X ] {\displaystyle \sigma ={\sqrt {D[X]}}} отождествляется с риском портфеля.
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.
Климат
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
ru.wikipedia.org
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ это:
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ (arithmetic mean) Средняя величина, полученная путем сложения всех членов числового ряда и деления суммы на число членов, например среднее арифметическое значение 7, 20, 107 и 350 равно 484/4 = 121. Однако средняя величина не позволяет судить о разбросе чисел. сравни: среднее геометрическое значение (geometric mean).Финансы. Толковый словарь. 2-е изд. — М.: "ИНФРА-М", Издательство "Весь Мир". Брайен Батлер, Брайен Джонсон, Грэм Сидуэл и др. Общая редакция: д.э.н. Осадчая И.М.. 2000.
.
dic.academic.ru
Что такое среднее арифметическое?
Вячеслав богданов
Число Среднее (Mean), Среднее Арифметическое (Arithmetic Mean) - усредненное значение, характеризующее какую-либо группу наблюдений; вычисляется путем сложения чисел из этого ряда и последующего деления полученной суммы на количество просуммированных чисел. Если одно или несколько чисел, входящих в группу, значительно отличаются от остальных, то это может привести к искажению получаемого среднего арифметического значения. Поэтому в данном случае предпочтительнее пользоваться средним геометрическим значением (geometric mean) (оно вычисляется аналогичным образом, но здесь определяется среднее арифметическое логарифмов величин наблюдений, а затем находится его антилогарифм) или - что применяется чаще всего - находить среднее значение (median) (среднее значение из серии величин, расположенных в порядке возрастания) . Еще одним методом получения среднего значения какой-либо величины из группы наблюдений является определение моды (mode) - показателя (или набора показателей) , оценивающего наиболее частые проявления какой-либо переменной величины; чаще этот метод используется для определения среднего значения в нескольких сериях опытов.
Например: числа 1 и 99, складываем и делим на два:
(1+99)/2=50 - среднее арифметическое
Если взять числа (1,2,3,15,59)/5=16 - среднее арифметическое, и т. д. и т. п.
Daimon
Вячаслав богданов ответил неправильно!!! !
Ндо своими слвами!
Среднее арифметическое - это среднее значение между двумя значениями.... Находится как суму чисел деленное на ихуоличество.. . Или просто, если два числа находятся вокруг когото числа (вернее между ними в порядке есть какое то число) , то это число и будет ср. ар. !
6 + 8... ср ар = 7
Компания ронин
Среднее арифметическое набора чисел определяется как их сумма, деленная на их количество. То есть сумма всех чисел набора делится на количество чисел в этом наборе.
Наиболее простой случай - найти среднее арифметическое двух чисел x1 и x2. Тогда их среднее арифметическое X = (x1+x2)/2. Например, X = (6+2)/2 = 4 - среднее арифметическое чисел 6 и 2.
2
Общая формула для нахождения среднего арифметического n чисел будет выглядеть так: X = (x1+x2+...+xn)/n. Ее можно также записать в виде: X = (1/n)Σxi, где суммирование ведется по индексу i от i = 1 до i = n.
К примеру, среднее арифметическое трех чисел X = (x1+x2+x3)/3, пяти чисел - (x1+x2+x3+x4+x5)/5.
3
Интерес представляет ситуация, когда набор чисел представляет собой члены арифметической прогрессии. Как известно, члены арифметической прогрессии равны a1+(n-1)d, где d - шаг прогрессии, а n - номер члена прогрессии.
Пусть a1, a1+d, a1+2d,...a1+(n-1)d - члены арифметической прогрессии. Их среднее арифметическое равно S = (a1+a1+d+a1+2d+...+a1+(n-1)d)/n = (na1+d+2d+...+(n-1)d)/n = a1+(d+2d+...+(n-2)d+(n-1)d)/n = a1+(d+2d+...+dn-d+dn-2d)/n = a1+(n*d*(n-1)/2)/n = a1+dn/2 = (2a1+d(n-1))/2 = (a1+an)/2. Таким образом среднее арифметическое членов арифметической прогрессии равно среднему арифметическому его первого и последнего членов.
4
Также справедливо свойство, что каждый член арифметической прогрессии равен среднему арифметическому предыдущего и последующего члена прогрессии: an = (a(n-1)+a(n+1))/2, где a(n-1), an, a(n+1) - идущие друг за другом члены последовательности.
Виктория гордиенко
Сре́днее арифмети́ческое (в математике и статистике) — одна из наиболее распространенных мер центральной тенденции, представляющая собой сумму всех зафиксированных значений, деленную на их количество.
У этого термина существуют и другие значения, см. среднее значение.
Сре́днее арифмети́ческое (в математике и статистике) — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех зафиксированных значений, делённую на их количество.
Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
Содержание [показать]
Введение [править | править вики-текст]
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (\bar{x} \,, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и \bar{x} \, в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда \bar{x} \, (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i = \frac{1}{n} (x_1+\cdots+x_n).
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.
Примеры [править | править вики-текст]
Для трёх чисел необходимо сложить их и разделить на 3:
\frac{x_1 + x_2 + x_3}{3}.
Для четырёх чисел необходимо сложить их и разделить на 4:
\frac{x_1 + x_2 + x_3 + x_4}{4}.
Или проще 5+5=10, 10:2. Потому что мы складывали 2 числа, а значит, сколько чисел складываем, на столько и делим.
Непрерывная случайная величина [править | править вики-текст]
Для непрерывно распределённой величины f(x) среднее арифметическое на отрезке [a;b] определяется через определённый интеграл: Некоторые проблемы применения среднего Отсутствие робастности [править Основная статья: Робастность в статистикеХотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическ
Анти-ликвидатор. Адам
Это складываеш числа и их делиш соклько было вот так 33+66+99= складываеш 33+66+99= 198 и делиш сколько было зачит у нас 3 числа это 33 66 и 99 и надо что у нас получилось поделить вот так : 33+66+99=198:3=66 это средня орефметическое
Читайте также
![Знак виктория пальцами значение Знак виктория пальцами значение]() Знак виктория пальцами значение
Знак виктория пальцами значение![Знаки на пальцах рук значение Знаки на пальцах рук значение]() Знаки на пальцах рук значение
Знаки на пальцах рук значение![Знаки пальцами рук значение у молодежи Знаки пальцами рук значение у молодежи]() Знаки пальцами рук значение у молодежи
Знаки пальцами рук значение у молодежи![Экологические знаки и их значение Экологические знаки и их значение]() Экологические знаки и их значение
Экологические знаки и их значение![Среднее значение функции на отрезке Среднее значение функции на отрезке]() Среднее значение функции на отрезке
Среднее значение функции на отрезке![Среднее значение Среднее значение]() Среднее значение
Среднее значение![Среднее арифметическое значение формула Среднее арифметическое значение формула]() Среднее арифметическое значение формула
Среднее арифметическое значение формула![Христианские символы и знаки и их значение Христианские символы и знаки и их значение]() Христианские символы и знаки и их значение
Христианские символы и знаки и их значение![Сущность и значение средних величин Сущность и значение средних величин]() Сущность и значение средних величин
Сущность и значение средних величин![Среднее и действующее значение синусоидального тока Среднее и действующее значение синусоидального тока]() Среднее и действующее значение синусоидального тока
Среднее и действующее значение синусоидального тока![Среднее арифметическое значение Среднее арифметическое значение]() Среднее арифметическое значение
Среднее арифметическое значение![Расчет среднего значения Расчет среднего значения]() Расчет среднего значения
Расчет среднего значения
 Знак виктория пальцами значение
Знак виктория пальцами значение Знаки на пальцах рук значение
Знаки на пальцах рук значение Знаки пальцами рук значение у молодежи
Знаки пальцами рук значение у молодежи Экологические знаки и их значение
Экологические знаки и их значение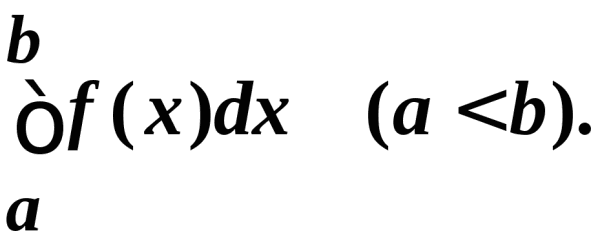 Среднее значение функции на отрезке
Среднее значение функции на отрезке Среднее значение
Среднее значение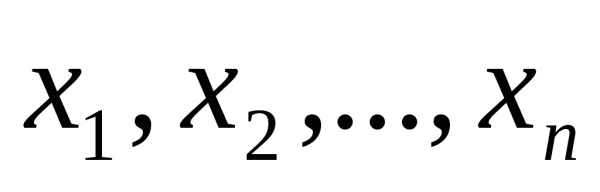 Среднее арифметическое значение формула
Среднее арифметическое значение формула Христианские символы и знаки и их значение
Христианские символы и знаки и их значение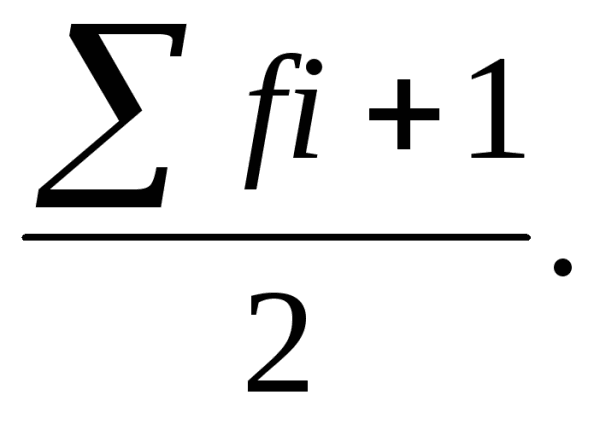 Сущность и значение средних величин
Сущность и значение средних величин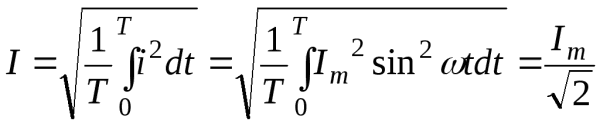 Среднее и действующее значение синусоидального тока
Среднее и действующее значение синусоидального тока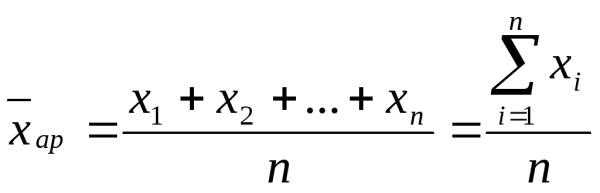 Среднее арифметическое значение
Среднее арифметическое значение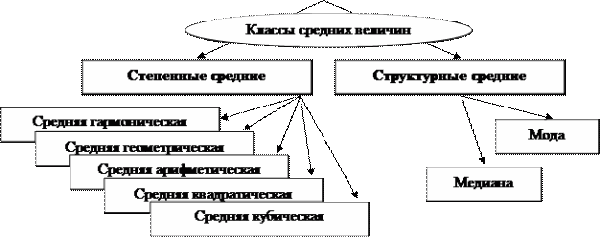 Расчет среднего значения
Расчет среднего значения