Окружность
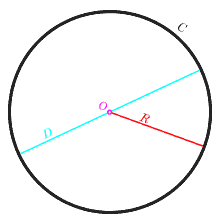 Окружность (C), её центр (O), радиус (R) и диаметр (D)
Окружность (C), её центр (O), радиус (R) и диаметр (D)
Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки[1]. Эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Внутренность окружности называется кругом; в зависимости от подхода, круг может включать граничные точки (то есть окружность) или не включать их.
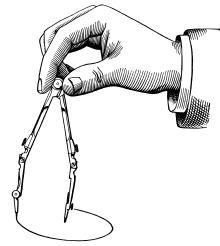 Построение окружности с помощью циркуля
Построение окружности с помощью циркуля
Практическое построение окружности производится с помощью циркуля. Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.
Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Далее всюду буква R {\displaystyle R} обозначает радиус окружности.
Хорды, дуги и касательные

Диаметр окружности

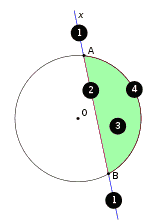
1 — секущая, 2 — хорда AB (отмечена красным), 3 — сегмент (отмечен зелёным), 4 — дуга

Секторы круга
Окружность разбивает свою плоскость на две части[2] — конечную внутреннюю (круг) и бесконечную внешнюю, состоящую из точек плоскости, удалённых от центра более чем на R {\displaystyle R} .
Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D = 2 R , {\displaystyle D=2R,} он делит окружность и круг на две равные части и поэтому является их осью симметрии. Диаметр больше любой другой хорды[3].
Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)[3].
Любые две не совпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Для заданной окружности имеют место следующие свойства[3].
- Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
- Равным хордам соответствуют равные дуги, и наоборот.
- При пересечении двух хорд произведение отрезков, на которые точка пересечения делит одну из них, равно произведению отрезков другой.
 Касательная к окружности
Касательная к окружности
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности[4].
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Углы

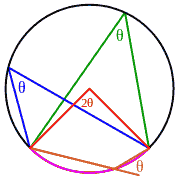
Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)

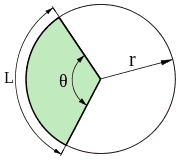
К расчёту длины дуги и хорды
Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан. С ростом угла значение его радианной меры меняется от 0 до 2 π . {\displaystyle 2\pi .}
Из определения радиана следует, что длина L {\displaystyle L} любой дуги окружности связана с центральным углом θ {\displaystyle \theta } , опирающимся на эту дугу, простым соотношением[5]: L = R θ . {\displaystyle L=R\theta .} Длина хорды, стягивающей ту же дугу, равна 2 R sin θ 2 . {\displaystyle 2R\sin {\theta \over 2}.} Отсюда следует, что длину всей окружности можно вычислить по формуле C = 2 π R . {\displaystyle \ C=2\pi R.}
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.
Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.
Свойства вписанных углов:
- Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
- Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
Другие свойства:
- Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
- Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
- Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.
Свойства
- Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Точка касания двух окружностей лежит на прямой, проходящей через их центры.
- Произведение длин расстояний от выбранной точки до двух точек пересечения окружности и секущей, проходящей через выбранную точку, не зависит от выбора секущей и равно абсолютной величине степени точки относительно окружности.
- Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равен абсолютной величине степени точки относительно окружности.
- Любая нормаль, проведенная внутрь окружности к любой её касательной, всегда постоянна по длине и совпадает с диаметром этой окружности как по направлению, так и по длине. Из последнего свойства вытекает следующее оптическое свойство окружности:
- Если источник света находится в центре окружности, а окружность является зеркалом, то после отражения от окружности-зеркала лучи снова соберутся в её центре (Собирающее оптическое свойство окружности).
Сводка формул
Длина окружности:
C = 2 π R = π D . {\displaystyle C=2\pi R=\pi D.}Радиус окружности:
R = C 2 π = D 2 . {\displaystyle R={\frac {C}{2\pi }}={\frac {D}{2}}.}Диаметр окружности:
D = C π = 2 R . {\displaystyle D={\frac {C}{\pi }}=2R.}Площадь круга радиуса R:
S = π R 2 = π D 2 4 . {\displaystyle S=\pi R^{2}={\frac {\pi D^{2}}{4}}.}Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:
S = π R 2 α 360 ∘ . {\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.}Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:
S = π R 2 α 360 ∘ − R 2 sin α 2 . {\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.}История
Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.
Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.
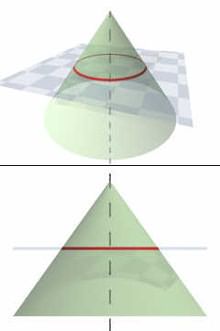 Окружность получается как сечение конуса плоскостью, перпендикулярной его оси
Окружность получается как сечение конуса плоскостью, перпендикулярной его оси
Аналитическая геометрия окружностей
С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.
Декартовы координаты
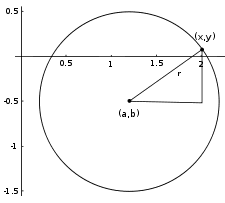 Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)
Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)
Общее уравнение окружности записывается как:
x 2 + y 2 + A x + B y + C = 0 , {\displaystyle x^{2}+y^{2}+Ax+By+C=0,}или
( x − x 0 ) 2 + ( y − y 0 ) 2 = R 2 , {\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}где
2 x 0 = − A , 2 y 0 = − B , 2 R = A 2 + B 2 − 4 C . {\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}Точка ( x 0 , y 0 ) {\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R {\displaystyle R} — её радиус.
Уравнение окружности радиуса R {\displaystyle R} с центром в начале координат:
x 2 + y 2 = R 2 . {\displaystyle x^{2}+y^{2}=R^{2}.}Уравнение окружности, проходящей через точки ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , {\displaystyle \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),} не лежащие на одной прямой (с помощью определителя):
| x 2 + y 2 x y 1 x 1 2 + y 1 2 x 1 y 1 1 x 2 2 + y 2 2 x 2 y 2 1 x 3 2 + y 3 2 x 3 y 3 1 | = 0. {\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}Тогда в явном виде координаты центра окружности определяются по формулам:
x 0 = − 1 2 y 1 ( x 2 2 + y 2 2 − x 3 2 − y 3 2 ) + y 2 ( x 3 2 + y 3 2 − x 1 2 − y 1 2 ) + y 3 ( x 1 2 + y 1 2 − x 2 2 − y 2 2 ) x 1 ( y 2 − y 3 ) + x 2 ( y 3 − y 1 ) + x 3 ( y 1 − y 2 ) {\displaystyle x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}} y 0 = 1 2 x 1 ( x 2 2 + y 2 2 − x 3 2 − y 3 2 ) + x 2 ( x 3 2 + y 3 2 − x 1 2 − y 1 2 ) + x 3 ( x 1 2 + y 1 2 − x 2 2 − y 2 2 ) x 1 ( y 2 − y 3 ) + x 2 ( y 3 − y 1 ) + x 3 ( y 1 − y 2 ) {\displaystyle y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}Окружность также можно описать с помощью параметрического уравнения:
{ x = x 0 + R cos φ y = y 0 + R sin φ , 0 ⩽ φ 2 π . {\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphiЕсли центр окружности совпадает с началом координат, функции принимают вид:
y = ± R 2 − x 2 . {\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}Полярные координаты
Окружность радиуса R {\displaystyle R} с центром в точке ( ρ 0 , ϕ 0 ) {\displaystyle \left(\rho _{0},\phi _{0}\right)} :
ρ 2 − 2 ρ ρ 0 cos ( ϕ − ϕ 0 ) + ρ 0 2 = R 2 . {\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}Если полярные координаты центра окружности ρ 0 = R , ϕ 0 = α , {\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:
ρ ( φ ) = 2 R cos ( φ − α ) , α − π 2 ⩽ φ ⩽ α + π 2 . {\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.}Если же центр является началом координат, то уравнение будет иметь вид
ρ = R . {\displaystyle \rho =R.}Комплексная плоскость
На комплексной плоскости окружность задаётся формулой:
| z − z 0 | = R {\displaystyle \left|z-z_{0}\right|=R}или в параметрическом виде
z = z 0 + R e i t , t ∈ R . {\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .}Окружности в пространстве
В пространстве окружность радиуса R {\displaystyle R} с центром в точке M 0 ( x 0 , y 0 , z 0 ) {\displaystyle M_{0}(x_{0},y_{0},z_{0})} можно определить как контур диаметрального сечения сферы
( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R 2 {\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}}плоскостью
a ⋅ ( x − x 0 ) + b ⋅ ( y − y 0 ) + c ⋅ ( z − z 0 ) = 0 {\displaystyle a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0} ,где a , b , c {\displaystyle a,b,c} — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы
{ ( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 = R 2 , a ⋅ ( x − x 0 ) + b ⋅ ( y − y 0 ) + c ⋅ ( z − z 0 ) = 0. {\displaystyle {\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}}Например, при a = c ≠ 0 {\displaystyle a=c\neq 0} решения этой системы можно задать параметрически следующим образом:
{ x = x 0 + R a 2 + c 2 ⋅ ( c ⋅ cos t − a ⋅ b ⋅ sin t a 2 + b 2 + c 2 ) , y = y 0 + R ⋅ a 2 + c 2 a 2 + b 2 + c 2 ⋅ sin t , z = z 0 − R a 2 + c 2 ⋅ ( a ⋅ cos t + b ⋅ c ⋅ sin t a 2 + b 2 + c 2 ) , t ∈ [ 0 ; 2 π ) . {\displaystyle {\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).}Касательные и нормали
Уравнение касательной к окружности в точке ( x 1 , y 1 ) {\displaystyle \left(x_{1},y_{1}\right)} определяется уравнением
( A 2 + x 1 ) x + ( B 2 + y 1 ) y + ( A 2 x 1 + B 2 y 1 + C ) = 0. {\displaystyle \left({\frac {A}{2}}+x_{1}\right)x+\left({\frac {B}{2}}+y_{1}\right)y+\left({\frac {A}{2}}x_{1}+{\frac {B}{2}}y_{1}+C\right)=0.}Уравнение нормали в той же точке можно записать как
x − x 1 2 x 1 + A = y − y 1 2 y 1 + B . {\displaystyle {\frac {x-x_{1}}{2x_{1}+A}}={\frac {y-y_{1}}{2y_{1}+B}}.}Концентрические и ортогональные окружности
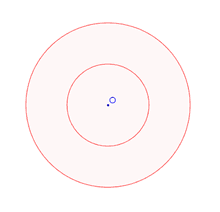 Концентрические окружности
Концентрические окружности
Окружности с общим центром, но разными радиусами, называются концентрическими. Две окружности, заданные уравнениями:
x 2 + y 2 + A 1 x + B 1 y + C 1 = 0 , x 2 + y 2 + A 2 x + B 2 y + C 2 = 0 {\displaystyle x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=0,\;\;\;x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}=0}являются концентрическими в том и только в том случае, когда A 1 = A 2 {\displaystyle A_{1}=A_{2}} и B 1 = B 2 . {\displaystyle B_{1}=B_{2}.}
Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие
A 1 A 2 + B 1 B 2 = 2 ( C 1 + C 2 ) . {\displaystyle A_{1}A_{2}+B_{1}B_{2}=2\left(C_{1}+C_{2}\right).}Дополнительные сведения
Определение треугольников для одной окружности
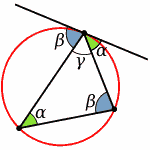 Через вершину треугольника проведена касательная к описанной окружности
Через вершину треугольника проведена касательная к описанной окружности
- Треугольник ABC называется вписанным в окружность (A,B,C), если все три его вершины A, B и C лежат на этой окружности. При этом окружность называется описанной окружностью треугольника ABC (См. Описанная окружность).
- Касательная к окружности, проведенная через любую вершину вписанного в неё треугольника антипараллельна стороне треугольника, противоположной данной вершине.
- Треугольник ABC называется описанным около окружности (A',B',C'), если все три его стороны AB, BC и CA касаются этой окружности в некоторых точках соответственно C', A' и B'. При этом окружность называется вписанной окружностью треугольника ABC (См. Вписанная окружность).
Варианты определения окружности
| В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 22 января 2016 года. |
- Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом (Определение через угол, опирающийся на диаметр окружности).
- Окружность с хордой AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под постоянным углом с одной стороны, равным вписанному углу дуги AB, и под другим постоянным углом с другой стороны, равным 180 градусов минус вписанный угол дуги AB, указанный выше (Определение через вписанный угол).
- Фигура состоящая из таких точек X , {\displaystyle X,} что отношение длин отрезков AX и BX постоянно: A X B X = c ≠ 1 , {\displaystyle {\frac {AX}{BX}}=c\neq 1,} является окружностью (Определение через окружность Аполлония).
- Фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками, также является окружностью (Определение через теорему Пифагора для произвольного прямоугольного треугольника, вписанного в окружность, с гипотенузой, являющейся диаметром окружности).
- Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Если через произвольную точку M внутри неё провести любые хорды AB, CD, EF и т. д., тогда справедливы равенства: A M ⋅ M B = C M ⋅ M D = E M ⋅ M F = … {\displaystyle AM\cdot {MB}=CM\cdot {MD}=EM\cdot {MF}=\dots } . Равенства всегда будут выполняться независимо от выбора точки M и направлений проведенных через неё хорд (Определение через пересекающиеся хорды).
- Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Если через произвольную точку M вне её провести две касательные до точек их касания с окружностью, например, A и B, тогда их длины всегда будут равны: M A = M B {\displaystyle MA=MB} . Равенство всегда будет выполняться независимо от выбора точки M (Определение через равные касательные).
- Окружность — замкнутая, самонепересекающаяся фигура, обладающая следующим свойством. Отношение длины любой её хорды к синусу любого её вписанного угла, опирающегося на эту хорду, есть величина постоянная, равная диаметру этой окружности (Определение через теорему синусов).
- Окружность — это частный случай эллипса, у которого расстояние между фокусами равно нулю (Определение через вырожденный эллипс).
Связанные определения для двух окружностей
- Две окружности, имеющие общий центр, называются концентрическими.
- Две окружности, имеющие лишь одну общую точку, называются касающимися внешним образом, если их круги не имеют других общих точек, и внутренним образом, если их круги лежат один внутри другого.
- Две окружности, имеющие две общие точки, называются пересекающимися. Их круги (ими ограниченные) пересекаются по области, называемой двойным круговым сегментом.
- Углом между двумя пересекающимися (или касающимися) окружностями называется угол между их касательными, проведенными в общей точке пересечения (или касания).
- Также углом между двумя пересекающимися (или касающимися) окружностями можно считать угол между их радиусами (диаметрами), проведенными в общей точке пересечения (или касания).
- Поскольку для любой окружности её радиус (или диаметр) и касательная, проведенные через любую точку окружности, взаимно перпендикулярны, то радиус (или диаметр) можно считать нормалью к окружности, построенной в данной её точке. Следовательно, два типа углов, определенных в двух предыдущих двух пунктах, всегда будут равны между собой, как углы со взаимно перпендикуярными сторонами.
- Две окружности, пересекающиеся под прямым углом, называются ортогональными. Окружности можно считать ортогональными, если они образуют прямой угол друг с другом.
- Радикальная ось двух окружностей — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырех касательных, проведенных к двум данным окружностям из любой точки M данного геометрического места точек.
Определения углов для двух окружностей
- Угол между двумя пересекающимися окружностями — угол между касательными к окружностям в точке пересечения этих окружностей. Оба угла между двумя пересекающимися окружностями равны.
- Угол между двумя непересекающимися окружностями — угол между двумя общимикасательными к двум окружностям, образуемый в точке пересечения этих двух касательных. Точка пересечения этих двух касательных должна лежать между двумя окружностями, а не со стороны одной из них (этот угол не рассматривается). Оба вертикальных угла между двумя непересекающимися окружностями равны.
Ортогональность
- Две окружности, пересекающиеся под прямым углом, называются ортогональными. Окружности можно считать ортогональными, если они образуют прямой угол друг с другом.
- Две пересекающиеся в точках A и B окружности с центрами O и O' называются ортогональными, если являются прямыми углы OAO' и OBO'. Именно это условие гарантирует прямой угол между окружностями. В этом случае перпендикулярны радиусы (нормали) двух окружностей, проведенные в точку их пересечения. Следовательно, перпендикулярны и касательные двух окружностей, проведенные в точку их пересечения. Касательная окружности перпендикулярна радиусу (нормали), проведенному в точку касания. Обычно угол между кривыми — это угол между их касательными, проведенными в точке их пересечения.
- Возможно другое дополнительное условие. Пусть две пересекающиеся в точках A и B окружности имеют середины пресекающихся дуг в точках C и D, то есть дуга AС равна дуге СB, дуга AD равна дуге DB. Тогда эти окружности называются ортогональными, если являются прямыми углы СAD и СBD.
Связанные определения для трех окружностей
- Три окружности называются взаимно касающимися (пресекающимися), если любые две из них касаются (пресекаются) друг друга.
- В геометрии радикальный центр трёх окружностей — это точка пересечения трёх радикальных осей пар окружностей. Если радикальный центр лежит вне всех трёх окружностей, то он является центром единственной окружности (радикальной окружности), которая пересекает три данные окружности ортогонально.
Лемма Архимеда
Лемма Архимеда. Если окружность вписана в сегмент окружности, стягиваемый хордой B C {\displaystyle BC} , и касается дуги в точке A 1 {\displaystyle A_{1}} , а хорды — в точке A 2 {\displaystyle A_{2}} , то прямая A 1 A 2 {\displaystyle A_{1}A_{2}} является биссектрисой угла B A 1 C {\displaystyle BA_{1}C} . Лемма Архимеда играет важную роль при построении изоциркулярного преобразования.
Доказательство
Пусть G {\displaystyle G} — гомотетия, переводящая малую окружность в большую. Тогда ясно, что A 1 {\displaystyle A_{1}} является центром этой гомотетии. Тогда прямая B C {\displaystyle BC} перейдет в какую-то прямую a {\displaystyle a} , касающуюся большой окружности, а A 2 {\displaystyle A_{2}} перейдет в точку на этой прямой и принадлежащей большой окружности. Вспомнив, что гомотетия переводит прямые в параллельные им прямые, понимаем, что a ∥ B C {\displaystyle a\parallel BC} . Пусть G ( A 2 ) = A 3 {\displaystyle G(A_{2})=A_{3}} и D {\displaystyle D} — точка на прямой a {\displaystyle a} , такая, что ∠ C A 3 D {\displaystyle \angle CA_{3}D} — острый, а E {\displaystyle E} — такая точка на прямой a {\displaystyle a} , что ∠ B A 3 E {\displaystyle \angle BA_{3}E} — острый. Тогда, так как a {\displaystyle a} — касательная к большой окружности ∠ C A 3 D {\displaystyle \angle CA_{3}D} = {\displaystyle =} ∠ C B A 3 {\displaystyle \angle CBA_{3}} = ∠ B A 3 E = ∠ B C A 3 {\displaystyle =\angle BA_{3}E=\angle BCA_{3}} . Следовательно △ B C A 3 {\displaystyle \bigtriangleup BCA_{3}} — равнобедренный, а значит ∠ B A 1 A 3 = ∠ C A 1 A 3 {\displaystyle \angle BA_{1}A_{3}=\angle CA_{1}A_{3}} , то есть A 1 A 2 {\displaystyle A_{1}A_{2}} — биссектриса угла ∠ B A 1 C {\displaystyle \angle BA_{1}C} .
Теорема Декарта для радиусов четырех попарно касающихся окружностей
Основная статья: Теорема Декарта (геометрия)Теорема Декарта утверждает, что радиусы любых четырёх взаимно касающихся окружностей удовлетворяют некоторому квадратному уравнению. Их иногда называют окружностями Содди.
Многомерное обобщение
Обобщённую окружность можно определить для любой математической структуры, где задано понятие расстояния. В частности, обобщением для многомерного евклидова пространства является гиперсфера; в трёхмерном пространстве это обычная сфера. В сферической геометрии важную роль играют окружности на сфере, центр которых совпадает с центром сферы («большие круги»).
ru.wikipedia.org
Как рассчитать длину окружности и периметр круга?
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
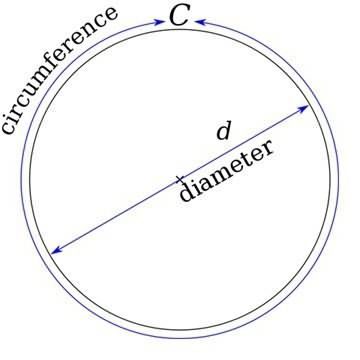
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
До того как рассчитать длину окружности, потребуется договориться о том, какая буква что обозначает. Это удобно записать в таблице.
| Величина | Обозначение |
| радиус | r |
| диаметр | d |
| длина окружности | l |
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
l =2π * r.
Здесь и далее π берется округленным. Чаще всего в задачах используют значение 3,14. Но иногда нужна большая точность и тогда применяют такое число: 3,14159.

Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
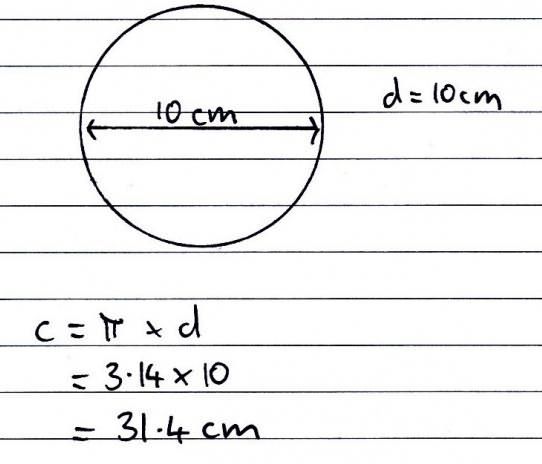
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l1 = 18,84 см, l2= 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
syl.ru
Как вычислить диаметр окружности?
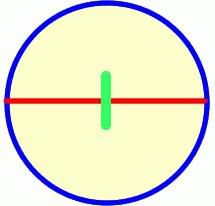
Для начала, давайте разберемся, что такое окружность и в чем ее отличие от круга. Возьмите ручку или карандаш красного цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, – это окружность. А вот синее содержимое внутри нее - и есть круг. 
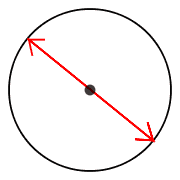
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
 Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
D = 2 * R
К примеру, радиус - 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить длину окружности. Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
L = Пи * D
D = L / Пи
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
D = 7 / 3, 14
D = 21, 98
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S – в данном случае площадь фигуры. Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении размера кольца, что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
fb.ru
Какова формула длины окружности?
Как найти длину окружности?
Coolwark
Длину окружности можно найти одним из представленных способов:
- если известен диаметр окружности, то формула выглядит так — L = ПD
- если известен радиус окружности, то формула имеет следующий вид — L = 2Пr.
Где П — 3,14.
Дольфаника
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности

Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.

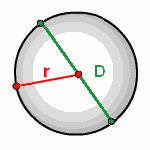
r - это радиус
D - диаметр
π - приблизительно 3,14
Но окружность - это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью

Афанасий44
Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.
Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи - величина постоянная и равна 3,14.
Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Selena-ursus
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса -- диаметр и число π, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=πd или L=2πR, где L -- значение длины окружности, получаемое умножением числа π (3,14) на величину радиуса окружности или двойного диаметра.
Elearner
Формула длины окружности
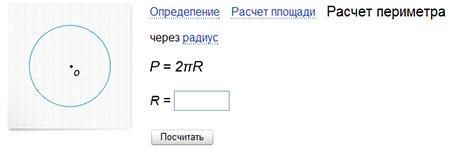
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе. Введите в Яндексе формула длины окружности, он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку "Посчитать".
Edvard
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.14.
Chela
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.
88Summertime88
Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
L=πd
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Формула:
L=2πR
Moreljuba
Итак, длина окружности может быть рассчитана, например, вот таким способом как L=πd (где d - это будет диаметр).
А вот если известен радиус, то длину вы уже сможете найти так L=2πr (где r будет соответственно радиус вашей окружности).
Ну а пи считаем равным 3,14.
Annet007
Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга. Она вас, при решении геометрических задач, еще не раз выручит.

Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
bolshoyvopros.ru
Доброго времени суток, киньте формулу, для определения длинны окружности по диаметру
Степанова а.С.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О) , называемой центром окружности . Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ) , соединяющий две любые точки окружности и проходящий через её центр, называется диаметром. Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.) . Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д. ) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра) . Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра) , то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С, длину диаметра буквой D, тогда отношение их будет иметь вид С : D. Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С : D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С : D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416. Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи) . Тогда отношение длины окружности к диаметру запишется так: С : D = π. Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С : D = π, то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 • 3,14 = 17,27 {м) .
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6 : 3,14 = 40 (см) .
Найдём теперь радиус колеса:
40 : 2 = 20 (см) .
Читайте также
![Укажите формулу классического определения вероятности Укажите формулу классического определения вероятности]() Укажите формулу классического определения вероятности
Укажите формулу классического определения вероятности![Методы определения длины корневого канала Методы определения длины корневого канала]() Методы определения длины корневого канала
Методы определения длины корневого канала![Закон джоуля ленца формула и определение Закон джоуля ленца формула и определение]() Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение![Закон ампера определение и формула Закон ампера определение и формула]() Закон ампера определение и формула
Закон ампера определение и формула![Акт определение Акт определение]() Акт определение
Акт определение- Актив определение
![Бетон определение Бетон определение]() Бетон определение
Бетон определение![Власть определение Власть определение]() Власть определение
Власть определение- Выберите один из вариантов определения истины это
![Гражданская война определение Гражданская война определение]() Гражданская война определение
Гражданская война определение![Дайте определение понятию авария Дайте определение понятию авария]() Дайте определение понятию авария
Дайте определение понятию авария![Генетическое определение пола кратко Генетическое определение пола кратко]() Генетическое определение пола кратко
Генетическое определение пола кратко

 Укажите формулу классического определения вероятности
Укажите формулу классического определения вероятности Методы определения длины корневого канала
Методы определения длины корневого канала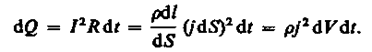 Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение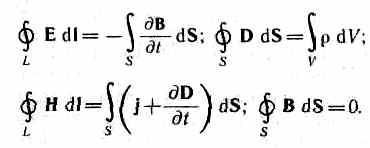 Закон ампера определение и формула
Закон ампера определение и формула Акт определение
Акт определение Бетон определение
Бетон определение Власть определение
Власть определение Гражданская война определение
Гражданская война определение Дайте определение понятию авария
Дайте определение понятию авария Генетическое определение пола кратко
Генетическое определение пола кратко