Закон Ампера это:
Закон Ампера| |
||||||||||||
| Электричество · Магнетизм | ||||||||||||
Электростатика
|
||||||||||||
| См. также: Портал:Физика |
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:
.Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
|
Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока в проводнике и векторному произведению элемента длины проводника на магнитную индукцию : |
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.
Модуль силы Ампера можно найти по формуле:
где — угол между векторами магнитной индукции и тока.
Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():
Содержание
|
Два параллельных проводника
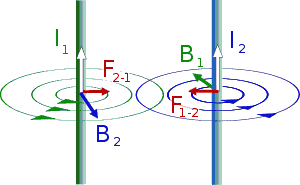 Два бесконечных параллельных проводника в вакууме
Два бесконечных параллельных проводника в вакууме
Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи и . Требуется найти силу, действующую на единицу длины проводника.
В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током в точке на расстоянии создаёт магнитное поле с индукцией
где — магнитная постоянная.
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).
Модуль данной силы ( — расстояние между проводниками):
Интегрируем, учитывая только проводник единичной длины (пределы от 0 до 1):
Полученная формула используется в СИ для установления численного значения магнитной постоянной . Действительно, ампер, являющийся одной из основных единиц СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10−7 ньютона»[1].
Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная равна Н/А² или, что то же самое, Гн/ м точно.
Проявления
| Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
- Электродинамическая деформация шин (токопроводов) трёхфазного переменного тока на подстанциях при воздействии токов короткого замыкания.
- Раздвигание токопроводов рельсотронов при выстреле.
Применение
| Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
- Принцип работы электромеханических машин (движение части обмотки ротора к части обмотки статора).
- Электродинамическое сжатие плазмы, например, в токамаках, установках Z-пинч (англ.).
- Электродинамический метод прессования.
Примечания
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин.
См. также
- Сила Лоренца
- Закон Ампера о циркуляции
Для улучшения этой статьи желательно?:
|
- Магнетизм
- Электричество
- Электротехника
- Физические законы
- Сила
- Магнитостатика
- Андре-Мари Ампер
Wikimedia Foundation. 2010.
dic.academic.ru
§ 111. Закон Ампера. Взаимодействие параллельных токов
Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию В:
dF = I[dl, В]. (111.1)
Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера (см. (111.1)) вычисляется по формуле
dF = IBdlsin, (111.2)
где a — угол между векторами dl и В.
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1и I2 (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора b1 задается правилом правого винта, его модуль по формуле (110.5) равен
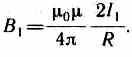
Направление силы dF1, с которой поле B1действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол между элементами тока I2 и вектором B1 прямой, равен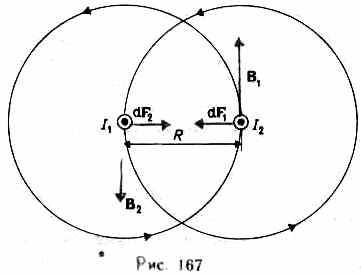
dF1=I2B1dl, или, подставляя значение для В1, получим
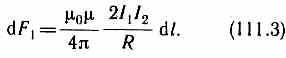
Рассуждая аналогично, можно показать, что сила dF2, с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна
![]()
Сравнение выражений (111.3) и (111.4) показывает, что
dF1=dF2,
т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой
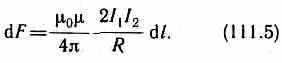
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).
45.Закон Фарадея и его вывод из закона сохранения энергии
Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э. д. с, электромагнитной индукции ξiопределяются только скоростью изменения магнитного потока, т. е.
![]()
Теперь необходимо выяснить знак ξi. В § 120 было показано, что знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали связано с током правилом правого винта (см. § 109). Следовательно, выбирая определенное положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с.
![]()
Знак минус показывает, что увеличение потока (dФ/dt>0) вызывает э.д.с.
ξξi
потока (dФ/dti>0,
т. е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока, выведенного в 1833 г.
Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона сохранения энергии, как это впервые сделал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоскости контура, и может свободно перемещаться (см. рис. 177). Под действием силы Ампера F, направление которой показано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампера производит работу (см.(121.1)) dA=IdФ, где dФ — пересеченный проводником магнитный поток.
Если полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за время dt (ξIdt) будет складываться из работы на джоулеву теплоту (I2Rdt) и работы по перемещению проводника в магнитном поле (IdФ):
![]()
откуда
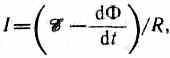
где-dФ/dt=ξiесть не что иное, как закон Фарадея (см. (123.2)).
Закон Фарадея можно сформулировать еще таким образом: э.д.с. ξi электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э.д.с. ξiне зависит от способа изменения магнитного потока.
Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим
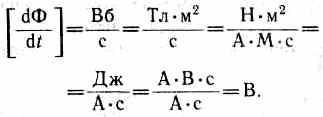
Какова природа э.д.с. электромагнитной индукции? Если проводник (подвижная перемычка контура на рис. 177) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противоположно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления (за направление электрического тока принимается движение положительных зарядов). Таким образом, возбуждение э.д.с. индукции при движении контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.
Согласно закону Фарадея, возникновение э.д.с. электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора ЕВэтого поля по любому неподвижному контуру L проводника представляет собой э.д.с. электромагнитной индукции:
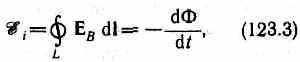
47.. Индуктивность контура. Самоиндукция
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре:
Ф=LI, (126.1)
где коэффициент пропорциональности Lназывается индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:
1 Гн=1 Вб/А=1В•с/А.
Рассчитаем индуктивность бесконечно длинного соленоида. Согласно (120.4), полный магнитный поток через соленоид
(потокосцепление) равен 0(N2I/l)S. Подставив это выражение в формулу (126.1), получим
![]()
т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости вещества, из которого изготовлен сердечник соленоида.
Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды (см. §93).
Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э.д.с. самоиндукции

Если контур не деформируется и магнитная проницаемость среды не изменяется (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L=const и
![]()
где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем.
Если ток со временем возрастает, то
dI/dt>0 и ξs
направлен навстречу току, обусловленному внешним источником, и тормозит его возрастание. Если ток со временем убывает, то dI/dts>0, т. е. индукционный
ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.
59.Уравнения Максвелла для электромагнитного поля
Введение Максвеллом понятия тока смещения привело его к завершению созданной им единой макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1. Электрическое поле (см. § 137) может быть как потенциальным (eq), так и вихревым (ЕB), поэтому напряженность суммарного поля Е=ЕQ+ЕB. Так как циркуляция вектора eq равна нулю (см. (137.3)), а циркуляция вектора ЕB определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля
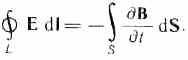
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):
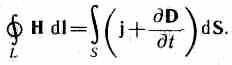
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D:
![]()
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , то формула (139.1) запишется в виде
![]()
4. Теорема Гаусса для поля В (см. (120.3)):
![]()
Итак, полная система уравнений Максвелла в интегральной форме: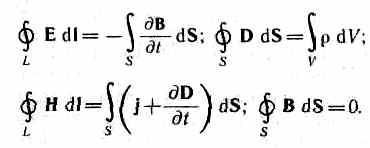
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные не сегнетоэлектрические и не ферромагнитные среды):
D=0E,
В=0Н,
j=E,
где 0и 0 — соответственно электрическая и магнитная постоянные, и — соответственно диэлектрическая и магнитная проницаемости, — удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Для стационарных полей (Е=const и В=const) уравнения Максвелла примут вид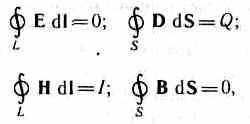
т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):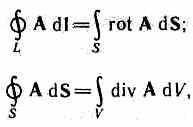

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная
и дифференциальная — эквивалентны. Однако когда имеются поверхности разрыва — поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):
D1n=D2n, E1=E2, B1n=B2n, H1= H2
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.
Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, смогла объяснить не только уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения (см. § 138), что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3•108 м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.
К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.
Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе
от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.
Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Так, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.
Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.
44.. Диа- и парамагнетизм
Всякое вещество является магнетиком, т. е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны.
Ради простоты предположим, что электрон в атоме движется по круговой орбите. Если орбита электрона ориентирована относительно вектора В произвольным образом, составляя с ним угол а (рис. 188), то можно доказать, что она приходит в такое движение вокруг В, при котором вектор магнитного момента рm, сохраняя постоянным угол а, вращается вокруг направления В с некоторой угловой скоростью. Такое движение в механике называется прецессией. Прецессию вокруг вертикальной оси, проходящей через точку опоры, совершает, например, диск волчка при замедлении движения.
Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.
В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в данном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома (он равен векторной сумме магнитных моментов (орбитальных и спиновых) составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (например, Bi, Ag, Au, Cu), большинство органических соединений, смолы, углерод и т. д.
Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные — вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.
У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается. К парамагнетикам относятся редкоземельные элементы, Pt, Al и т. д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным.
Из рассмотрения явления парамагнетизма следует, что его объяснение совпадает с объяснением ориентационной (дипольной) поляризации диэлектриков с полярными молекулами (см. §87), только электрический момент атомов в случае поляризации надо заменить магнитным моментом атомов в случае намагничения.
Подводя итог качественному рассмотрению диа- и парамагнетизма, еще раз отметим, что атомы всех веществ являются носителями диамагнитных свойств. Если магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является парамагнетиком; если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамагнетиком.
Ферромагнетики и их свойства
Помимо рассмотренных двух классов веществ — диа- и парамагнетиков, называемых слабомагнитными веществами, существуют еще сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т. е. они намагничены даже при отсутствии внешнего магнитного поля. К ферромагнетикам кроме основного их представителя — железа (от него и идет название «ферромагнетизм») — относятся, например, кобальт, никель, гадолиний, их сплавы и соединения.
StudFiles.ru
Закон Ампера. Магнитное взаимодействие токов. Определение единицы силы тока в системе СИ.
Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:
F = B I l sinα,
где α — угол между векторами магнитной индукции и тока,
B — индукция магнитного поля,
I — сила тока в проводнике,
l — длина проводника.
Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.
Если проводник имеет произвольную формулу и поле неоднородно, то Закон Ампера принимает вид:
dF = I B dl sinα,
где dF — сила, с которой магнитное поле действует на бесконечно малый проводник с током I,
dl — элемент длины проводника.
Размерность:
[dF] = Н
[I] = A,
[B] = Н / (А · м),
[l] = м.
Направление силы dF определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила правой руки.
Сила dF максимальна, когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (α = 90, sinα = 1):
dFmax = I B dl
Явление взаимного притяжения разноименных и отталкивания одноименных электрических зарядов во многом сходны с явлениями притяжения и отталкивания одноименных полюсов магнита
Ампер – сила не изменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2*10-7Н на каждый метр длины.
Сила, с которой магнитное поле действует на проводник с током, называется силой Ампер
studopedia.ru
Обсуждение:Закон Ампера
Проект:Физика (Уровень III, Важность «высокая»)
|
|||
| III (в развитии) |
Эта статья по шкале оценок статей Проекта:Физика имеет III уровень. | ||
|
Высокая |
Важность этой статьи для проекта Физика: высокая | ||
Чем помочь:
|
|||
Ссылка на англ. вики
ссылка на англ. вики неправильная. идет на Ampère's circuital law, а должно на Ampère's force law 192.84.134.230 12:50, 2 мая 2008 (UTC)
Исправил. --gribozavr 21:08, 27 июня 2008 (UTC)Сила Лоренца есть сила Ампера.
Для восстановления исторической справедливости, надо бы упомянуть, что сила Лоренца вышла из силы Ампера.
Сила тока равна заряду, проходящему по проводнику со скоростью V I = q ∗ V {\displaystyle I=q*V}
Ток электронов при увеличении заряда на обкладке конденсатора I = Q t {\displaystyle I={\frac {Q}{t}}} Этот ток путают с током по проводнику для силы Ампера. Когда силу тока пишут как I = q s e k {\displaystyle I={\frac {q}{sek}}}
Формула Ампера F → A = I → × H → {\displaystyle {\vec {F}}_{A}={\vec {I}}\times {\vec {H}}}
I → = q V → {\displaystyle {\vec {I}}=q{\vec {V}}}
Отсюда сила Ампера - Лоренца F L = q [ V → × H → ] {\displaystyle F_{L}=q[{\vec {V}}\times {\vec {H}}]} --Михаил Певунов 16:18, 20 января 2016 (UTC)
Под кат
Просьба убрать под кат довольно длинный кусок текста, который я выделил такими скобками {{{текст}}}, а то у меня не получаетсяClothclub 04:39, 6 января 2016 (UTC)
- Убрал с помощью {{начало скрытого блока}} и {{конец скрытого блока}}. — Stannic(обс)(вкл)(выкл) 05:42, 6 января 2016 (UTC)
- Большое спасибо!!Clothclub 05:59, 6 января 2016 (UTC)
- А зачем вообще нужны эти выкладки? Википедия это не справочник и не учебник. Доказательства там совершено не нужны. Но главное, что википедия пишется по авторитетным источникам. В двух новых разделах нет ни одной ссылки. Нужны ссылки на источники. Пока это похоже на ВП:Оригинальное исследование. Alexei Kopylov 07:23, 6 января 2016 (UTC)
- Очень рад, что вы спросили. Во-первых, ссылка все-таки есть - на книгу Максвелла "Treatise on Electricity and Magnetism". Но вы правы: почти весь раздел "Закон Грассмана" я переписал из английской Википедии. Правда, та вещь, которую я доказал, там не доказывается, и это доказательство мне не удалось найти ни в одном источнике. Поэтому я его придумал самостоятельно и решил записать. Но я считаю, в случае очевидных вещей ссылки на авторитетные источники не нужны. Вам ведь не нужен авторитет, чтобы понять, что 2x2=4? Это тот же случай, просто немного более сложный и менее очевидный. Я же постарался сделать его более очевидным. Лично мне таких доказательств в Википедии никогда не хватало, и я надеюсь, что не только мне. Да, и я был бы рад, если бы кто-то озадачился и добавил эти ссылки, если он о них знает, исправил бы мои ошибки, если они есть, и т.д., а не просто бы все откатил назад. Потому что русская Википедия по сравнению с английской похожа на счастливое неведение.Clothclub 14:11, 6 января 2016 (UTC)
- Википедия - это не учебник, поэтому не удивительно, что вам не хватает доказательств в Википедии - вы видимо пытаетесь использовать ее как учебник. Доказательства в Википедии могут быть только, если они имеют самостоятельную значимость. То что вы не нашли доказательства, только ставить под сомнения их значимость. С другой стороны, есть Викиучебник в котором такие доказательства вполне уместны. Советую перенести ваши доказательства туда, а тут поставить на них ссылку при помощи Шаблон:Викиучебник. Alexei Kopylov 17:47, 6 января 2016 (UTC)
Диаметр БАКа рассчитывался для протона по этому уравнению.
q [ V × H ] = m p V 2 R {\displaystyle q[V\times H]=m_{p}{\frac {V^{2}}{R}}}
Слева центростремительная сила Лоренца, справа центробежная сила инерции.
Говорить о не выполнения третьего закона для сил инерции и Лоренца, мягко говоря, нельзя.--Михаил Певунов 17:31, 21 января 2016 (UTC)
Михаил Певунов, каким образом у вас получилось приравнять вектор к скаляру? Так, как вы пишете, писать нельзя. И потом, почему "говорить о не выполнения третьего закона для сил инерции и Лоренца, мягко говоря, нельзя"? В частном случае он вполне может выполняться, а вот в общем - нет. Чтобы доказать последнее, достаточно единственного примера. Этот пример - заряды движутся перпендикулярно друг другу. Выше я приводил ссылку на схему.Clothclub 02:18, 22 января 2016 (UTC)1.Если вы ознакомитесь с учебником физики, то узнаете, что работа, это скаляр, равна произведению вектора силы, на вектор перемещения. A = F → × S → {\displaystyle A={\vec {F}}\times {\vec {S}}}
Вы путаете понятие скалярной величины с модулем векторного произведения.2. Если заряды движутся перпендикулярно друг другу, то сила Лоренца равна нулю, по определению.
3. Не вижу смысла обсуждать с вами проблемы физики. Ваши тексты сохранены по недосмотру редакции.--Михаил Певунов 14:04, 24 января 2016 (UTC)
Михаил Певунов, вы еще и векторное произведение от скалярного не отличаете. Думаю, с учебником физики в первую очередь не мешало бы ознакомиться именно вам. Лучше пишите поменьше, чтобы не сбивать людей с толку.Clothclub 14:49, 24 января 2016 (UTC)Статья нуждается в упрощении
Рисунок нуждается в корректировке. Круги могут ввести в заблуждение. Не понятно почему вектор Н перпендикулярен силовым линиям магнитного поля.
Надо обозначить окружность с радиусом R c центром в точке 1 и показать ее как Н1 на всей окружности. Тогда в точке 2 ,будет начало вектора Н1
Показать окружность с центром в точке 2, тогда в точке 1 будет начало вектора Н2
H → 2 = m o I 2 2 p i R {\displaystyle {\vec {H}}_{2}=m_{o}{\frac {I_{2}}{2piR}}}
Тогда перемножением векторов получаем
F 1 − 2 = I → 1 × H → 2 = m o I 2 2 p i R × I 1 = m o I 2 I 1 2 p i R {\displaystyle F_{1-2}={\vec {I}}_{1}\times {\vec {H}}_{2}=m_{o}{\frac {I_{2}}{2piR}}\times I_{1}=m_{o}{\frac {I_{2}I_{1}}{2piR}}}
Михаил Певунов, к чему этот пустой трёп? Если вы считаете, что рисунок должен быть улучшен - хотя бы предложите свой вариант. Я не вижу, чтобы вы предложили какой-нибудь рисунок. Более того, хоть рисунок рисовал и не я, но мне он кажется удачным и лично меня вполне устраивает. Я даже думаю, если вы попытаетесь нарисовать то, о чем вы говорите, вы поймете, что ошибаетесь. Потому что вы опять начинаете приравнивать вектор к скаляру. Эта ошибка у вас и во всех нижеследующих формулах.Clothclub 02:18, 22 января 2016 (UTC)Почему статья начинается с уравнения d F = j → × B → d V {\displaystyle dF={\vec {j}}\times {\vec {B}}dV}
Диаметр проводника у Ампера не был переменным, переменными были ток и радиус.
Автор хотел образованность свою показать, вот и показал нелепое.
Лучше бы он показал два дифференциальных уравнения.
1. d F = H → 2 × I → 1 d I {\displaystyle 1.dF={\vec {H}}_{2}\times {\vec {I}}_{1}dI}
2. d F = I → 1 × H → 2 d H {\displaystyle 2.dF={\vec {I}}_{1}\times {\vec {H}}_{2}dH}
Оба уравнения имеют одинаковое решение. Это значит, что для силы Ампера третий закон соблюдается. .--Михаил Певунов 00:29, 20 января 2016 (UTC)
И что тут то делают всякие форумные неучи. V → 2 = V 2 {\displaystyle {\vec {V}}^{2}=V^{2}} Произведение векторов может дать вектор, а может и скаляр, тогда определяется только модуль, без направления.
Понял?
Да?
--Михаил Певунов 17:58, 24 января 2016 (UTC)
- Рекомендую участникам дискуссии прочитать ВП:ЭП, ВП:НО. — stannic(обс)(вкл)(выкл) 18:10, 24 января 2016 (UTC)
Прошу редакцию посмотреть правильные рисунки по теме.
Щелкнуть по ссылке. Нужные кадры два первых. Когда запустится первый, щелкнуть по нему, он остановится.Затем хапустить и щелкнуть по аторому. Остальные кадры на хвост сели. Так работает Ютуб слайдов. https://you.be/71qKy0AV2xk
youtu в черном списке. Вставьте в ссылку после you буковки tu и просмотрите на любом форумном редакторе. --Михаил Певунов 15:32, 24 января 2016 (UTC)
- Он не зря в чёрном списке. По вопросам физики (и по многим другим вопросам) youtube не считается в Википедии авторитетным источником, поэтому приводить ссылки на него не нужно. Лучше всего привести ссылки на публикацию в рецензируемом журнале или учебник. — stannic(обс)(вкл)(выкл) 18:13, 24 января 2016 (UTC)
Отвечать в данной теме должен чел, имеющий физико-математическое образование. Я предлагаю посмотреть, как улучшить рисунок, а вы предлагаете мне сначала опубликовать его в платном журнале.
Я пишу, что решение уравнения вашего АИ d F = i → B → d V {\displaystyle dF={\vec {i}}{\vec {B}}dV} дает размерность I*B*метр, потому как размерность плотности тока метр-2, а объем метр3, но вы не понимаете абсурдность этой размерности.--Михаил Певунов 10:59, 25 января 2016 (UTC)
Узнали бы Ампер, Био и Савар свои законы в данной статье.
В их времена никаких векторов не было. Они собирали свои установки, наблюдали, замеряли и обнаружив закономерности, обнародовали свои законы.
Ампер замерял силовое взаимодействие двух двух параллельных прямых проводников при различных параметрах постоянного тока и на различных расстояниях между ними. Вопрос о направлении токов перед ним не стоял.
То, что силы взаимодействия направлены по кратчайшей прямой, перпендикулярно проводникам, для него было очевидным.
Также очевидным для него было, что силовое взаимодействие проводников, как и гравитационное взаимодействие, подчиняется третьему закону Ньютона. Иначе это будет не взаимодействие, что он и показал в своем законе F 1.2 = k I 1 I 2 2 p i R = − F 2.1 = − k I 2 I 1 2 p i R {\displaystyle F_{1.2}=k{\frac {I_{1}I_{2}}{2piR}}=-F_{2.1}=-k{\frac {I_{2}I_{1}}{2piR}}}
Ампер практически замерил силу силу взаимодействия бесконечных проводников на симметричных отрезках длиной Δ = 1 m {\displaystyle \Delta =1m} на расстоянии R = 1 метр при силе тока 1 ампер. Которая по современным данным равна 2*10-7 ньютон
Тогда его формула приобретает вид 2*10-7 = 2 ∗ 10 − 7 k 1 ∗ 1 2 p i {\displaystyle 2*10^{-7}k{\frac {1*1}{2pi}}}
Отсюда магнитная постоянная k = m 0 = 2 p i ∗ 2 ∗ 10 − 7 = 4 p i ∗ 10 − 7 {\displaystyle k=m_{0}=2pi*2*10^{-7}=4pi*10^{-7}} Это известное выражение, но не известно откуда оно взялось. Непонятно зачем в статье формула https://upload.wikimedia.org/math/e/c/2/ec267329d3cda88fe6bca032e7b716e2.png Зачем в знаменатель и числитель умножен на 2.
Чуть раньше Био с Саваром установили, сила напряженности магнитного поля Н расстоянии R направлена перпендикулярно радиусу и и пропорциональна m o I 1 2 p i R = H 1 {\displaystyle m_{o}{\frac {I_{1}}{2piR}}=H_{1}}
А так как, эта сила должна быть пропорциональна току I 2 = q V → {\displaystyle I_{2}=q{\vec {V}}} то формула силы Ампера записывалась F = q ∗ V ∗ H . {\displaystyle F=q*V*H.}
И н потому что так им хотелось, а потому что такое замерялось.
То, что я тут изложил, не моя самодеятельность, а взято из учебников, но в доступном для понимания школьниками. Данная статья доступна для людей уже владеющих физикой и математикой.
А оно им надо.
Непонятно, зачем в силу Ампера вводить плотность тока i → = I → S {\displaystyle {\vec {i}}={\frac {\vec {I}}{S}}} c размерностью ампер/метр2, но тогда следует писать
d F → = i → ∗ S ∗ H → d L = I → H → d L {\displaystyle d{\vec {F}}={\vec {i}}*S*{\vec {H}}dL={\vec {I}}{\vec {H}}dL}ru.wikipedia.org
Закон ампера
Валерий янович
У Валентины каша в голове и она дала закон Ома. Вот закон Ампера. Сила, действующая на проводник со стороны магнитного поля равна произведению модуля вектора магнитной индукции на силу тока, на длину проводника, находящнегося в магнитном поле и на синус угла между направлением тока и направлением вектора магнитной индукции. F = BILsina
Валентина конишевская
Сила тока прямо пропорционально напряжению и обратно пропорциональна сопротивлению. Откурой учебник выучи все формулы при параллельном соединении при последовательном, это стыдно не знать, проще в физике нет материала. Нос в учебник!
Дамир садыков
Закон Ампера - один из важнейших и полезнейших законов в электротехнике, без которого немыслим научно-технический прогресс. Этот закон был впервые сформулирован в 1820 году Андре Мари Ампером. Подробнее формула и принцип закона описан в источнике...
Читайте также
![Укажите формулу классического определения вероятности Укажите формулу классического определения вероятности]() Укажите формулу классического определения вероятности
Укажите формулу классического определения вероятности![Закон джоуля ленца формула и определение Закон джоуля ленца формула и определение]() Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение- Актив определение
![База данных определение База данных определение]() База данных определение
База данных определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение- Выберите один из вариантов определения истины это
![Генетические механизмы определения пола Генетические механизмы определения пола]() Генетические механизмы определения пола
Генетические механизмы определения пола![Власть определение Власть определение]() Власть определение
Власть определение![Бетон определение Бетон определение]() Бетон определение
Бетон определение![Вопросы определения Вопросы определения]() Вопросы определения
Вопросы определения![Акт определение Акт определение]() Акт определение
Акт определение![Дайте определение понятию авария Дайте определение понятию авария]() Дайте определение понятию авария
Дайте определение понятию авария
 Укажите формулу классического определения вероятности
Укажите формулу классического определения вероятности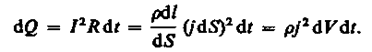 Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение База данных определение
База данных определение Болезнь определение
Болезнь определение Генетические механизмы определения пола
Генетические механизмы определения пола Власть определение
Власть определение Бетон определение
Бетон определение Вопросы определения
Вопросы определения Акт определение
Акт определение Дайте определение понятию авария
Дайте определение понятию авария