Область определения это:
Область определения Запрос «Отображение» перенаправляется сюда. Cм. также другие значения.В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
|
Определения
- Нестрогое определение: функция — это «закон», по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
- Строгое определение: функция или отображе́ние — это бинарное отношение, обладающее свойством:
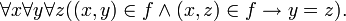
- Функция называется инъективной, если

Обозначения
 ,
,  или
или  для отображения F множества X в множество Y;
для отображения F множества X в множество Y;
- Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или
 .).
.). - Множество Y называется о́бластью значе́ний отображения F.(обозначается E(F), или
 ).
).
- Множество X называется о́бластью определе́ния отображения F (обозначается D(F), или
 , y = F(x) или
, y = F(x) или  или
или  . Используется также обратная польская запись: y = xF, а иногда y = xF.
. Используется также обратная польская запись: y = xF, а иногда y = xF.
- Элементы x называют аргументами функции, а соответствующие элементы y — значениями функции.
Связанные определения
- Пусть дано отображение
 , и
, и  . Тогда суже́нием функции F на M называется функция
. Тогда суже́нием функции F на M называется функция  , определяемая равенством
, определяемая равенством  . Это определение подчёркивает, что фиксация области определения является частью определения функции.
. Это определение подчёркивает, что фиксация области определения является частью определения функции.
- F является продолжением функции
 на множество
на множество  . Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
. Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
- Пусть
 . Тогда о́бразом множества M называется подмножество множества Y, определяемое равенством
. Тогда о́бразом множества M называется подмножество множества Y, определяемое равенством  .
.
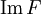 .
.
- Пусть задано отображение
 ,
,  и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент
и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент  должен иметь ровно один образ, но элемент
должен иметь ровно один образ, но элемент  может не иметь прообразов либо иметь один или несколько.
может не иметь прообразов либо иметь один или несколько.
- Например, пусть дана функция
 , где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
, где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
- Например, пусть дана функция
- Пусть задано отображение
 , и
, и  . Тогда множество
. Тогда множество  называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
- Например, пусть
 , и F(x) = sinx. Тогда
, и F(x) = sinx. Тогда  .
.
- Например, пусть
- Пусть
 . Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством
. Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством  .
.
- Например, пусть
 , и F(x) = cosx. Тогда
, и F(x) = cosx. Тогда ![F\left(\left[0,\;\frac{\pi}{2}\right]\right)=[0,\;1]](data:image/gif;base64,R0lGODdhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=) ,
, ![F^{-1}([0,\;1])=\bigcup\limits_{n\in\Z}\left[-\frac{\pi}{2}+2\pi n,\;\frac{\pi}{2}+2\pi n\right]](data:image/gif;base64,R0lGODdhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=) .
.
- Например, пусть
Свойства
Свойства прообразов и образов
 ;
; ;
; ;
; . Заметим отсутствие равенства в этом случае.
. Заметим отсутствие равенства в этом случае.
Классы функций
При необходимости можно различать отображения в зависимости от природы множеств X и Y. Если X и Y — числовые множества, такие, как 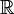 или
или 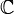 , то отображение называют функцией. Если X или Y многомерны, например,
, то отображение называют функцией. Если X или Y многомерны, например, 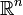 или
или 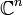 , то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
, то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
Вариации и обобщения
- многозначная функция
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Пусть даны множества 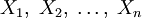 и множество Y, тогда упорядоченное множество всех кортежей
и множество Y, тогда упорядоченное множество всех кортежей 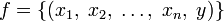 называется функцией n аргументов тогда и только тогда, когда для любых
называется функцией n аргументов тогда и только тогда, когда для любых 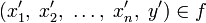 и
и 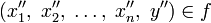 из
из 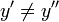 следует, что
следует, что ![x_{n}' \neq x_{n}'',\forall x\in [1,\;n]\cap\Z](http://i.zna4enie.ru/3/kak-oboznachaetsja-oblast-opredelenija-funkcii_40.png) .[1]
.[1]
Примечания
- ↑ Кудрявцев Л. Д. Курс математического анализа. — том 1. — М.: Высшая школа, 1981. — с. 8.
См. также
- Композиция функций
- График функции
- Сюръективность
- Инъективность
- Биективность
- Функция с множеством значений {0, 1}
- Функциональное уравнение
Литература
- Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Wikimedia Foundation. 2010.
dic.academic.ru
Область определения функции это:
Область определения функцииОбласть определения функции — множество, на котором задаётся функция.
Содержание
|
Определение
Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения.
Более формально, пусть задано отображение , которое отображает множество в , то есть: ; тогда
- множество называется областью определения функции
- и обозначается , или (от англ. domain «область»).
Обычно предполагается, что , из-за чего понятие области определения выглядит тавтологией: «область определения функции — это область, где определена функция». Для того, чтобы придать чёткий смысл данному понятию, рассматривается некоторое более широкое множество, которое называется областью отправления, и тогда область определения функции — это такое подмножество множества (которое и есть область отправления функции), где для каждого элемента определено значение функции .
Этот факт коротко записывают в виде: .
Примеры
Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.
Числовые функции
Числовые функции — это функции, относящиеся к следующим двум классам:
- вещественнозначные функции вещественного переменного — это функции вида ;
- а, также, комплекснозначные функции комплексного переменного это функции вида ,
где и — множества вещественных и комплексных чисел соответственно.
Тождественное отображение
Область определения функции совпадает с областью отправления ( или ).
Гармоническая функция
Область определения функции : представляет собой комплексную плоскость без нуля
и не совпадает с областью отправления (вся комплексная плоскость).
Дробно-рациональные функции
Область определения дробно-рациональной функции вида
представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения
.Эти точки называются полюсами функции .
Мера
Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.
Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.
Например, определённый интеграл представляет собой функцию ориентированного промежутка.
Функционал
Пусть — семейство отображений из множества в множество . Тогда можно определить отображение вида . Такое отображение называется функционалом.
Если, например, фиксировать некоторую точку , то можно определить функцию , которая принимает в «точке» то же значение, что и сама функция в точке .
См. также
- Область значений функции
Литература
- Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
- Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
- ISBN 5-02-014844-X
- А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
- А. Н. Колмогоров «Что такое функция» // «Квант». — М.: «Наука», 1970. — В. 1. — С. 27-36. — ISSN 0130-2221.
Для улучшения этой статьи по математике желательно?:
|
- Функции
Wikimedia Foundation. 2010.
dic.academic.ru
Область определения функции
Остановимся на процедуре нахождения области определения функции.
1. В том случае, когда функция задана в аналитическом виде (посредством формулы)
![]() (3.1)
(3.1)
и никаких ограничений или оговорок более не имеется, область ее определения устанавливается исходя из правил выполнения математических операций, входящих в формулу f в (3.1). Эти ограничения хорошо известны: подкоренное выражение в корне четной степени не может быть отрицательным, знаменатель дроби не может быть равным нулю, выражение под знаком логарифма должно быть только
положительным, а также некоторые другие. Приведем здесь два примера.
Пример 1. у = log2 (x2 — 5x + 6).
Область определения этой функции находится из условия x2 — 5x + 6 > 0. Поскольку x = 2 и x = 3 — корни квадратного трехчлена, стоящего под знаком логарифма, то это условие выполняется на двух полубесконечных интервалах: (-![]() , 2) и (3,
, 2) и (3,![]() ). На рис. 3.4 выделена заштрихованная полоса, в которой график функции отсутствует.
). На рис. 3.4 выделена заштрихованная полоса, в которой график функции отсутствует.

Рис. 3.4
Пример 2. у = arcsin ![]() .
.
Область определения этой функции находится из совокупности двух условий: аргумент под знаком arcsin не может быть по модулю больше единицы и знаменатель аргумента не должен равняться нулю, т.е.
![]()
Двойное неравенство эквивалентно двум более простым неравенствам: х + 2 ≥ 1 и х + 2 ≤ -1. Отсюда получаем, что область определения функции состоит из двух полубесконечных промежутков: (-![]() , -3] и (-1,
, -3] и (-1,![]() ). Запретная точках = -2 сюда не попадает. В отличие от предыдущего примера концы полуинтерваловвходят в область определения функции.
). Запретная точках = -2 сюда не попадает. В отличие от предыдущего примера концы полуинтерваловвходят в область определения функции.
2. Область определения функции задана вместе с функцией f(x).
Пример 3. у = 3x-4/3 + 2, 1 ≤ х ≤ 4.
3. Функция имеет определенный прикладной характер, и область ее существования определяется также и реальными значениями входящих параметров (например, задачи с физическим смыслом).
Определение 2. Функция у =f(x) называется четной (симметрия относительно оси Оу), если для любых значений аргумента из области ее определения выполнено равенство
![]()
Определение 3. Функция у = f(x) называется нечетной (симметрия относительно начала координат О), если выполнено условие:
![]()
Например, функции у = х2 и у = cos x являются четными, а функции у = x3 и у = sin x— нечетными.
Приложения в экономике
Приведем примеры использования функций в области экономики.
1. Кривые спроса и предложения. Точка равновесия. Рассмотрим зависимости спроса D (demand) и предложения S (supply) от цены на товар Р (price). Чем меньше цена, тем больше спрос при постоянной покупательной способности населения. Обычно зависимость D отР имеет вид ниспадающей кривой (рис. 3.5, а):
![]() (3.2)
(3.2)
где а < 0. В свою очередь предложение растет с увеличением цены на товар, и потому зависимость S отР имеет следующую характерную форму:
![]() (3.3)
(3.3)
где b ≥ 1 (рис. 3.5, б). В формулах (3.2) и (3.3) с и d — так называемые экзогенные величины; они зависят от внешних причин (благосостояние общества, политическая обстановка и т.п.). Вполне понятно, что переменные, входящие в формулы (3.2) и (3.3), положительны, поэтому графики функций имеют смысл только в первой координатной четверти.

Рис. 3.5
Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению; это условие дается уравнением
![]()
и соответствует точке пересечения кривых D и S— это так называемая точка равновесия (рис. 3.6). Цена Ро, при которой выполнено условие (3.4), называется равновесной.

Рис. 3.6
При увеличении благосостояния населения, что соответствует росту величины с в формуле (3.2), точка равновесия М смещается вправо, так как кривая D поднимается вверх; при этом цена на товар растет при неизменной кривой предложения S.
2. Паутинная модель рынка. Рассмотрим простейшую задачу поиска равновесной цены. Это одна из основных проблем рынка, означающая фактически торг между производителем и покупателем (рис. 3.7).

Рис. 3.7
Пусть сначала цену P1 называет производитель (в простейшей схеме он же и продавец). Цена P1 на самом деле выше равновесной (естественно, всякий производитель стремится получить максимум выгоды из своего производства). Покупатель оценивает спрос D1 при этой цене и определяет свою цену Р2, при которой этот спрос D1 равен предложению. Цена Р2 ниже равновесной (всякий покупатель стремится купить подешевле). В свою очередь производитель оценивает спрос D2, соответствующий цене P2, и определяет свою цену Р3, при которой спрос равен предложению; эта цена выше равновесной. Процесс торга продолжается и при определенных условиях приводит к устойчивому приближению к равновесной цене, т.е. к "скручиванию" спирали. Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену Р0: ![]() Pn = P0.
Pn = P0.
StudFiles.ru
Объясните что такое область определения функции?
Объясните что такое область определения функции
(Лучшим отмечу только полный и понятный ответ!)
Семен аркадьевич
Область определения, это те значения Х, при которых функция имеет смысл.
Т. е. , например: y = 1/(x-2) в этом случае знаменатель не должен быть равен 0. А, следовательно, икс не должен быть равен 2, при котором знаменатель равен нулю. Таким образом в этом случае областью определения являются два участка:
икс от 0 до - бесконечности, и икс от нуля до плюс бесконечности... .
Или допустим, корень квадратный из икса - тогда мы знаем, что подкоренное выражение должно быть не меньше нуля. А значит область определения - это икс больше либо равен нулю.
Не следует путать с областью значений функции: это те значения Y котрые может принимать функция. Для примера можно рассмотреть синусоиду, областью значений которой является промежкток (на оси игриков) от -1 до +1 и т. п.
Нет сигнала
Область определения - это значения аргумента, при которых функция определена, т. е. если в знаменателе есть, например, х-2, то 2 - не в области определения, на ноль-то делить нельзя. Или если х под кв. корнем, то область определения от 0 до +бесконечности
Читайте также
![Как найти область значения функции Как найти область значения функции]() Как найти область значения функции
Как найти область значения функции![Акт определение Акт определение]() Акт определение
Акт определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Гражданское право определение Гражданское право определение]() Гражданское право определение
Гражданское право определение![Дайте определение понятию авария Дайте определение понятию авария]() Дайте определение понятию авария
Дайте определение понятию авария![Генетическое определение пола кратко Генетическое определение пола кратко]() Генетическое определение пола кратко
Генетическое определение пола кратко![Генетические механизмы определения пола Генетические механизмы определения пола]() Генетические механизмы определения пола
Генетические механизмы определения пола- Дать определение понятию индустриализация
![Деталь определение Деталь определение]() Деталь определение
Деталь определение![Закон джоуля ленца формула и определение Закон джоуля ленца формула и определение]() Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение![Земля определение Земля определение]() Земля определение
Земля определение![Что такое сила в физкультуре определение Что такое сила в физкультуре определение]() Что такое сила в физкультуре определение
Что такое сила в физкультуре определение
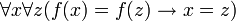
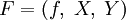 ,
, 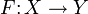 или
или 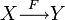 для отображения F множества X в множество Y;
для отображения F множества X в множество Y;
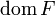 .).
.).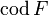 ).
). , y = F(x) или
, y = F(x) или 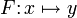 или
или 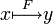 . Используется также обратная польская запись: y = xF, а иногда y = xF.
. Используется также обратная польская запись: y = xF, а иногда y = xF.
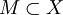 . Тогда суже́нием функции F на M называется функция
. Тогда суже́нием функции F на M называется функция 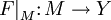 , определяемая равенством
, определяемая равенством 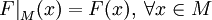 . Это определение подчёркивает, что фиксация области определения является частью определения функции.
. Это определение подчёркивает, что фиксация области определения является частью определения функции.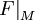 на множество
на множество 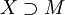 . Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.
. Можно рассматривать продолжения, обладающие различными свойствами, например аналитическое продолжение.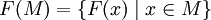 .
.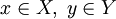 и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент
и y = F(x). Тогда x называется проо́бразом y, а y называется о́бразом x. Согласно определению отображения, каждый элемент 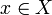 должен иметь ровно один образ, но элемент
должен иметь ровно один образ, но элемент 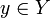 может не иметь прообразов либо иметь один или несколько.
может не иметь прообразов либо иметь один или несколько.
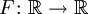 , где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.
, где F(x) = x2. Тогда y = − 1 не имеет прообразов; y = 0 имеет единственный прообраз x = 0; y = 1 имеет два прообраза: x1 = 1 и x2 = − 1.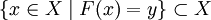 называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
называется по́лным проо́бразом элемента y. Полный прообраз обозначается F - 1(y).
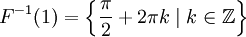 .
.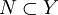 . Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством
. Тогда проо́бразом множества N называется подмножество множества X, определяемое равенством 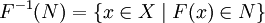 .
.
![F\left(\left[0,\;\frac{\pi}{2}\right]\right)=[0,\;1]](http://i.zna4enie.ru/e/kak-oboznachaetsja-oblast-opredelenija-funkcii_25.png) ,
, ![F^{-1}([0,\;1])=\bigcup\limits_{n\in\Z}\left[-\frac{\pi}{2}+2\pi n,\;\frac{\pi}{2}+2\pi n\right]](http://i.zna4enie.ru/b/kak-oboznachaetsja-oblast-opredelenija-funkcii_26.png) .
.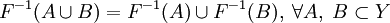 ;
;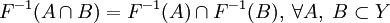 ;
;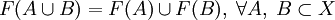 ;
;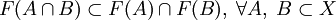 . Заметим отсутствие равенства в этом случае.
. Заметим отсутствие равенства в этом случае. Как найти область значения функции
Как найти область значения функции Акт определение
Акт определение Болезнь определение
Болезнь определение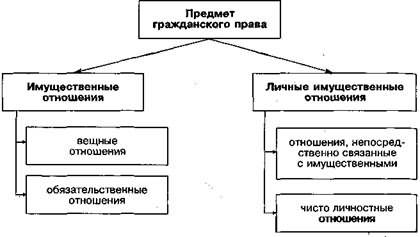 Гражданское право определение
Гражданское право определение Дайте определение понятию авария
Дайте определение понятию авария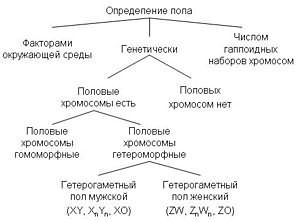 Генетическое определение пола кратко
Генетическое определение пола кратко Генетические механизмы определения пола
Генетические механизмы определения пола Деталь определение
Деталь определение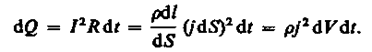 Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение Земля определение
Земля определение Что такое сила в физкультуре определение
Что такое сила в физкультуре определение