Классическое определение вероятности свойства вероятности

Классическое определение вероятности

Существуют различные подходы к определению вероятности события.

Одним из таких определений является так называемое классическое определение вероятности. Оно возникло на начальном этапе развития теории вероятностей.

При этом определении вероятностью события называется отноше­ние числа элементарных исходов, благоприятствующих данному собы­тию, к числу всех равновозможных элементарных исходов опыта.

Вероятность события А обозначают через Р(А). Если через m обо­значить число элементарных исходов, благоприятствующих событию А, а через n — число всех равновозможных элементарных исходов опыта, образующих полную группу событий, то

(19)

Установим некоторые свойства вероятности события.

Свойство 1. Вероятность события А есть неотрицательное число, заключенное между нулем и единицей: 0 < Р (А) < 1.

Это свойство непосредственно следует из равенства (19) по­скольку 0 < m < n.

Свойство 2. Вероятность достоверного события равна единице: P(U) = 1.

Это свойство следует из того, что достоверное событие наступает при каждом испытании (m = n).

Свойство 3. Вероятность невозможного события равна нулю: P(V) = 0.

В самом деле, невозможное событие ни при каком испытании не на­ступает (m = 0).

Свойство 4. (аддитивность). Если А и В — несовместные события, то вероятность их суммы равна сумме вероятностей: Р(А+В) = Р(А) + Р(В).

Пример. Пусть имеется 80 деталей, среди которых 60 исправных, а 20 бракованных. Найти вероятность того, что взятая наугад деталь ока­жется исправной.

Решение. Очевидно, что из числа всех деталей, т. е. из числа 80, нам благоприятствуют 60 и не благоприятствуют 20. Если, через А обозначим событие, что взятая деталь исправна, то согласно классиче­скому определению вероятность этого события равна отношению числа благоприятствующих элементарных исходов к числу всех равновоз­можных. Поэтому

Упражнения

  1. Среди 170 деталей, изготовленных на станке, оказалось 8 деталей, не отвечающих стандарту. Найдите вероятность выбора детали, не отвечающей стандарту.

  2. Телефонный номер состоит из шести цифр. Найдите вероятность того, что все цифры различные.

  3. Контролер, проверяя качество 500 изделий, установил, что 10 из них относится ко второму сорту, а остальные — к первому. Найди­ те вероятность выбора изделия первого сорта, выбора изделия второго сорта.

  4. На десяти карточках написаны цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Две из них вынимаются наугад и укладываются в порядке появления, затем читается полученное число. Найдите вероятность того, что число будет нечетным.

  5. На шести карточках написаны буквы в, д, з, о, у, х. После перета­совки вынимают наугад одну карточку за другой и раскладывают их в том порядке, в каком они были вынуты. Найдите вероятность того, что на карточках будет написано слово «воздух».

  6. В ящике находятся 6 красных и 9 белых шаров. Из ящика извле­чены три шара. Найдите вероятность того, что два из них окажутся красными.

6. Частота события. Статистическое определение вероятности

Классическое определение вероятности предполагает, что все эле­ментарные исходы равновозможные. О равновозможности исходов опы­та обычно заключают в силу соображений симметрии (например, как в случае идеальной игральной кости или монеты). Такие задачи на прак­тике встречаются довольно редко. Во многих случаях трудно указать основания для возможности считать, что все элементарные исходы равновозможные. В связи с этим появилась необходимость введения еще одного определения вероятности, которое получило название стати­стического. Это определение основано на таком понятии, как относи­тельная частота события.

Определение. Относительной частотой события или частотой называется отношение числа опытов, в которых появилось это собы­тие, к числу всех произведенных опытов.

Обозначим частоту события А через W(A), тогда по определению

где М - число опытов, в которых наступило событие А, а N - число всех произведенных опытов.

Частота события обладает следующими свойствами:

  1. Частота случайного события есть число, заключенное между нулем и единицей: 0 < W(A) < 1.

  2. Частота достоверного события U равна единице: W (U) = 1.

  3. Частота невозможного события V равна нулю: W (V) = 0

  4. Частота суммы двух несовместных событий А и В равна сумме частот этих событий: W(A +B) = W(A) + W(B)

Вероятностью Р(А) события А при статистическом ее определении называется частота W(A) данного события в серии, состоящей из боль­шого числа испытаний.

Пример. Из 600 наудачу взятых деталей 12 оказались бракованны­ми. Найти частоту появления бракованных деталей.

Решение. Так как в данном примере М = 12, а N = 600, то по опре­делению частоты имеем

Замечание. Кроме приведенных классического и статистического определений вероятности существует и так называемое геометрическое определение вероятности. Дело в том, что как классиче­ское, так и статистическое определения предполагают, что число эле­ментарных исходов конечно. Чтобы преодолеть этот недостаток, вво­дится геометрическое определение вероятности, которое состоит в том, что за вероятность принимается площадь некоторой области плос­кости, а за элементарный исход — точка этой области при условии, что площадь всей области элементарных исходов равна 1.

StudFiles.ru

Определение вероятности

Ясно, что каждое событие обладает той или иной степенью возможности своего наступления (своей реализации). Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число называется вероятностью события.

Вероятность события – есть численная мера степени объективной возможности наступления этого события.

Рассмотрим стохастический эксперимент и случайное событие А, наблюдаемое в этом эксперименте. Повторим этот эксперимент n раз и пусть m(A) – число экспериментов, в которых событие А произошло.

Отношение 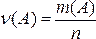(1.1)

называется относительной частотой события А в проведенной серии экспериментов.

Легко убедиться в справедливости свойств: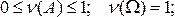

если А и В несовместны (АВ= 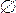), то ν(А+В) = ν(А) + ν(В) (1.2)

Относительная частота определяется только после проведения серии экспериментов и, вообще говоря, может меняться от серии к серии. Однако опыт показывает, что во многих случаях при увеличении числа опытов относительная частота приближается к некоторому числу. Этот факт устойчивости относительной частоты неоднократно проверялся и может считаться экспериментально установленным.

Пример 1.19.. Если бросить одну монету, никто не сможет предсказать, какой стороной она упадет кверху. Но если бросить две тонны монет, то каждый скажет, что примерно одна тонна упадет кверху гербом, то есть относительная частота выпадения герба примерно равна 0,5.

Если при увеличении числа опытов относительная частота события ν(А) стремится к некоторому фиксированному числу, то говорят, что событие А статистически устойчиво, а это число называют вероятностью события А.

Вероятностью события А называется некоторое фиксированное число Р(А), к которому стремится относительная частота ν(А) этого события при увеличении числа опытов, то есть,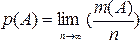

Это определение называют статистическим определением вероятности.

Рассмотрим некий стохастический эксперимент и пусть пространство его элементарных событий состоит из конечного или бесконечного (но счетного) множества элементарных событий ω1, ω2, …, ωi, … . предположим, что каждому элементарному событию ωi прописан некоторое число - рi, характеризующее степень возможности появления данного элементарного события и удовлетворяющее следующим свойствам:

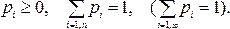(1.3)

Такое число pi называется вероятностью элементарного события ωi.

Пусть теперь А- случайное событие, наблюдаемое в этом опыте, и ему соответствует некоторое множество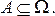

В такой постановке вероятностью события А называют сумму вероятностей элементарных событий, благоприятствующих А (входящих в соответствующее множество А):

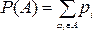(1.4)

Введенная таким образом вероятность обладает теми же свойствами, что и относительная частота, а именно:

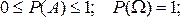и если АВ= 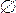(А и В несовместны),

то P(А+В) = P(А) + P(В)

Действительно, согласно (1.4)

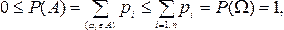
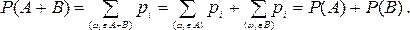
В последнем соотношении мы воспользовались тем, что ни одно элементарное событие не может благоприятствовать одновременно двум несовместным событиям.

Особо отметим, что теория вероятностей не указывает способов определения рi, их надо искать из соображений практического характера или получать из соответствующего статистического эксперимента.

В качестве примера рассмотрим классическую схему теории вероятностей. Для этого рассмотрим стохастический эксперимент, пространство элементарных событий которого состоит из конечного (n) числа элементов. Предположим дополнительно, что все эти элементарные события равновозможны, то есть вероятности элементарных событий равны p(ωi)=pi=p. Отсюда следует, что

Пример 1.20. При бросании симметричной монеты выпадение герба и «решки» равновозможны, их вероятности равны 0,5.

Пример 1.21. При бросании симметричного кубика все грани равновозможны, их вероятности равны 1/6.

Пусть теперь событию А благоприятствует m элементарных событий, их обычно называют исходами, благоприятствующими событию А. Тогда

(1.5)

Получили классическое определение вероятности: вероятность Р(А) события А равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов

Пример 1.22. В урне лежит m белых шаров и n черных. Чему равна вероятность вытащить белый шар?

Решение. Всего элементарных событий m+n. Они все равновероятны. Благоприятствующих событию А из них m. Следовательно, .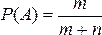

Из определения вероятности вытекают следующие ее свойства:

Свойство 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует собы­тию. В этом случае т=п, следовательно,

P(A)=m/n=n/n=1. (1.6)

Свойство 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае т = 0, следовательно, P(A)=m/n=0/n=0. (1.7)

Свойство 3.Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испы­тания. То есть, 0≤m≤n, значит, 0≤m/n≤1, следовательно, вероятность любого события удовлетворяет двойному неравенству 0≤P(A) ≤1. (1.8)

Сопоставляя определения вероятности (1.5) и относительной частоты (1.1), заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.

Однако, вычисление вероятности требует наличия предварительной информации о количестве или вероятностях благоприятствующих данному событию элементарных исходов. В случае отсутствия такой предварительной информации для определения вероятности прибегают к эмпирическим данным, то есть, по результатам стохастического эксперимента определяют относительную частоту события.

Пример 1.23. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей r (А) = 3/80.

Пример 1.24. По цели .произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели. r (А) =19/24.

Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это постоянное число можно принять за приближенное значение вероятности.

Подробнее и точнее связь между относительной частотой и вероятностью будет изложена далее. Теперь же проиллюстрируем свойство устойчивости на примерах.

Пример 1.25. По данным шведской статистики, относительная частота рождения девочек за 1935 г. по месяцам характеризуется сле­дующими числами (числа расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0.471; 0,478; 0,482; 0.462; 0,484; 0,485; 0,491; 0,482; 0,473

Относительная частота колеблется около числа 0,481, которое можно принять за приближеннее значение вероятности рождения девочек.

Заметим, что статистические данные различных стран дают примерно то же значение относительной частоты.

Пример 1.26. Многократно проводились опыты бросания монеты, в которых подсчитывали число появление «герба». Результаты нескольких опытов приведены в таблице.

Число бросаний Число появлений «герба» Относительная частота
0,5016 0,4989 0,5005

Здесь относительные частоты незначительно отклоняются от числа 0,5, причем тем меньше, чем больше число испытаний. Например, при 4040 испытаниях отклонение равно 0,0069, а при 24000 испытаниях - лишь 0,0005. Приняв во внимание, что вероятность появления «герба» при бросании монеты равна 0,5, мы вновь убеждаемся, что относительная частота колеблется около вероятности.

5. Классическое определение вероятности, ограниченность классического определения вероятности. Статистическая вероятность.

studopedia.ru

Классическое определение вероятности.

На самом деле это не определение, а метод вычисления вероятностей событий во вполне определенных и сильно ограниченных условиях.

Говорят, что случайный эксперимент удовлетворяет классическому определению вероятности (или классической вероятностной схеме), если:

· пространство элементарных событий состоит из конечного числа исходов

;

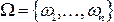· из соображений симметрии можно считать, что все элементарные исходы эксперимента являются равновозможными (т. е. ни один из исходов не имеет предпочтения перед другими).

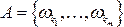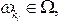
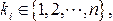
Согласно классическому определению вероятности вероятность любого события , 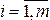равна отношению числа исходов 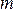, благоприятствующих событию 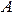, к общему числу исходов :

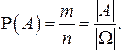
Свойства вероятности, непосредственно вытекающие из классического определения вероятности:

1°. для любого события А (доказательство очевидно).

2°. 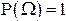(доказательство очевидно).

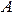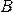3°. Если события и несовместны 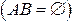, то

.

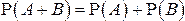▲ Пусть событию А благоприятствует 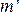исходов, а событию В - 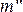исходов. Поскольку события А и В являются несовместными (т.е. не имеют общих исходов), то сумме 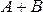благоприятствует 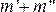исходов. Поэтому

.■

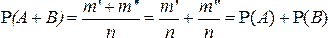Исходя из свойств 1° - 3° (и только!!!) вытекают также следующие свойства вероятности:

4°. .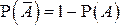

▲ Поскольку события 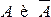образуют полную группу событий ( 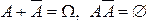), то из свойств 2° и 3° .■

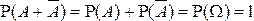5°. .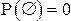

▲ Следует из свойств 2° и 4°, поскольку события .■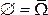

6°. .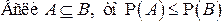

▲ Представим событие В в виде: 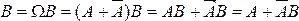. Поскольку события 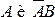являются несовместными, то из свойств 1° и 3° имеем: .■

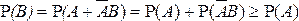7°. .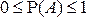

▲ Следует из свойств 2°, 5° и 6°, так как 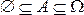(в частности, свойство 7° означает, что измерять вероятность в процентах некорректно).■

При решении задач с использованием классического определения вероятности, широко используются понятия комбинаторики. Напомним некоторые из них.

Размещением из N элементов некоторого множества по M элементов называется любой упорядоченный набор из M элементов данного множества. Число всех размещений равно .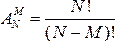

Если в упорядоченном наборе элементы могут повторяться, то этот набор называется размещением с повторениями. Число размещений с повторениями: равно .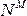

Перестановкой из N элементов некоторого множества называется размещение из N элементов по N. Число всех перестановок равно .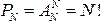

Сочетанием из N элементов некоторого множества по M элементов называется любое подмножество мощности M. Число всех сочетаний равно .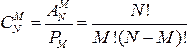

Пример 1.

Определить вероятность события А, заключающегося в том, что при бросании двух игральных костей, сумма очков не превысит 4.

Решение. В данном примере важно понимать, что если в качестве исхода эксперимента понимать значение суммы выпавших очков: или количество очков, выпавших на каждой из костей без учета порядка их следования: 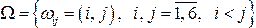, то исходы не являются равновозможными и классическое определение вероятности не применимо. Верное решение в соответствии с классическим определением вероятности можно получить, если только под исходом понимать количество очков, выпавших на каждой из костей с учетом порядка их следования: . В этом случае 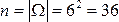, а 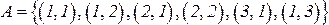. Поэтому .

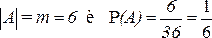Пример 2 (Урновая схема).

В урне находится N шаров, из которых M - белые. Из урны наугад извлекается n шаров. Какова вероятность того, что среди выбранных шаров окажется ровно m белых.

Решение. Исходами в данном эксперименте являются любые подмножества, содержащие n шаров, и они являются равновозможными (за счет слова «наугад»). Число всех исходов равно числу сочетаний из N по n: 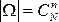. Каждый набор шаров, входящий в интересующее нас событие, состоит из m белых шаров, которые можно выбрать из M белых 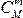способами. Независимо от выбора белых шаров, небелые шары можно выбрать 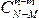способами. Поэтому общее число благоприятных исходов равно 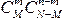. Из этого следует, что .


studopedia.ru

Свойства вероятностей. Классическое определение вероятности

Классическое определение вероятности

Виды случайных событий

Испытания и события

Событие названо случайным, если при осуществлении определенной совокупности условий S оно может либо произойти либо не произойти.

Совокупность условий S осуществлена или равносильна, произведено иcспытание.

Событие будем рассматривать как результат испытания.

Пример:

Стрелок стреляет по мишени, разделенной на 4 области.

Выстрел – испытание.

Попадание в определенную область мишени - событие.

Результат испытания – элемент выборки, а множество всех возможных элементов определяет выборочное пространство.

Событием называется подмножество выборочного пространства.

Элементарное (простое) событие - один элемент выборочного пространства.

Сложное событие – состоит более чем из одного элемента.

Графически выборочное пространство можно представить деревом событий

Пример:

В урне имеются цветные шары, из них на удачу берут 1 шар.

Излечение шара из урные – испытание.

Появление шара определенного цвета – событие.

События называют несовместными, если появление одного из них исключает появление других событий в одном итом же испытании.

Пример:

Брошена монета.

Появление “герба” исключает появление “надписи”.

События – появился “герб” и появилась “надпись” – несовместны.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

Появление хотя бы одного из событий полной группы – достоверное событие.

Если события, образующие полную группу попарно несовместны, то в результате испытания появится одно и только одно из этих событий.

Вероятность :

- число, характеризующее степень возможностей появления события.

- количественный способ учета неопределенности.

Отношение числа благоприятствующих событию А элементарных исходов к общему числу называют вероятностью события А.

m – число благоприятствующих событию А;

n – общее число.

Примечание:

Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.

1. вероятность достоверного события = 1

2. вероятность невозможного события = 0

3. вероятность случайного события – положительное число от 0 до 1

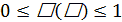
Относительная частота

- принадлежит к основным понятиям теории вероятности.

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.

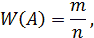
m – число появления события;

n – общее число испытаний;

Чем больше n, тем больше W стремится к P.

Определение вероятности не требует проведения испытания в действительности, т.е. не вероятность вычисления до опыта, а относительную частоту после опыта.

Из наблюдения следует, что если в одинаковых условиях произведены опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости.

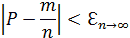
studopedia.ru

КЛАССИФИКАЦИЯ СОБЫТИЙ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ. СВОЙСТВА ВЕРОЯТНОСТИ

Под вероятностью, в широком смысле, понимают количественную меру неопределенности. Это – число, которое выражает степень уверенности наступления того или иного случайного события.

Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания. В дальнейшем для простоты мы будем опускать термин «случайный».

Мы определим испытание (опыт, эксперимент) как процесс, включающий определенные условия, которые приводят к одному из нескольких возможных исходов. Исходом опыта может быть результат наблюдения или измерения. Единичный, отдельный исход испытания называется элементарным событием.

Достоверное событие – это событие, которое обязательно произойдет в результате испытания. Например, если в урне содержатся только белые шары, то извлечение из нее белого шара есть событие достоверное.Другой пример, если мы подбросим вверх камень, то он обязательно упадет на Землю в силу действия закона притяжения, то есть результат этого опыта заведомо известен. Достоверные события условимся обозначать символом W.

Невозможное событие – это событие , которое не может произойти в результате данного опыта (испытания). Извлечение черного шара из урны с белыми шарами есть событие невозможное событие. Невозможное событие обозначим Æ.

Совместные события. Несколько событий, называются совместными, если в результате эксперимента наступление одного из них не исключает появление других. Например, в магазин вошел покупатель. События «в магазин вошел покупатель старше 60 лет» и «в магазин вошла женщина» - совместные, так как в магазин может войти женщина старше 60 лет.

Несовместные события. Несколько событий называются единственно возможными, если в результате испытания хотя бы одно из них обязательно произойдет (или одно, или два, или все события из рассматриваемой совокупности событий произойдут; одно точно произойдет).

Равновозможные события. Несколько событий называются равновозможными, если в результате испытания ни одно из них не имеет объективно большую возможность появления, чем другие. При бросании игральной кости появление каждой из ее граней – события равновозможные.

Противоположные события. Два единственно возможных события называются противоположными : если А – событие, то - противоположное ему событие. Купля и продажа определенного вида товара есть события противоположные.

Полная группа событий. Совокупность всех единственно возможных и несовместных событий называется полной группой событий.

Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементов исходов.

Обозначим число благоприятствующих событию А исходов через М, а число всех исходов через N ,тогда

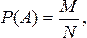(2.1)

где М – целое неотрицательное число, 0£ М£ N

Другой тип объективной вероятности определяется исходя из относительной частоты (частости) проявления события. Если, к примеру, некоторая фирма в течении времени провела опрос 1000 покупателей нового сорта напитка и 20 из них оценили его как вкусный, то мы можем оценить вероятность того, что потребителям понравится новый напиток как 20/1000=0,02. В этом примере 20- это частота наступления события, а 20/1000=0,02 – это относительная частота.

Относительной частотой события называется отношение числа

испытаний т, при которых событие появилось, к общему числу проведенных испытаний п. , (2.2)

где т – целое неотрицательное число, 0£ т£ п

Статистической вероятностью 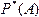называется относительная частота (частость) этого события А, вычисленная по результатам большого числа испытаний. Будем обозначать ее 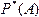: 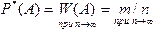. При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е. .

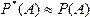Свойства вероятности, вытекающие из классического определения.

1. Вероятность достоверного события рана 1.

2. Вероятность невозможного события равна 0.

3. Вероятность случайного события есть положительное число, заключенное между 0 и 1.

4. Сумма вероятностей противоположных событий равна 1, то есть 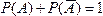или p+q=1,гдеp–вероятность события А , q–вероятность противоположного ему события.

Пример 1. Магазин в целях рекламы нового товара проводит лотерею, в которой 1 главный приз, 5 вторых призов, 100 третьих призов и 1000 четвертых призов. В конце рекламного дня выяснилось, что лотерейные билеты получили 10000 покупателей. По правилам розыгрыша, после извлечения выигрышного билета он не возвращается в урну, и покупатель не может получить более одного выигрыша. Чему равна вероятность того, что покупатель, который приобрел рекламируемый товар: а) выиграет первый приз; б) выиграет любой приз; в) не выиграет ни одного приза?

Решение. Определим событие А: «Покупатель выиграет первый приз». Согласно условию задачи в лотерее участвовало 10000 покупателей, отсюда общее число испытаний N= 10000, а число исходов, благоприятствующих событию А, М=1. Все исходы являются равновозможными, единственно возможными и несовместными элементарными событиями. Следовательно, по формуле классической вероятности: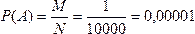

Соответственно, определим событие В: «Покупатель выиграл любой приз». Для этого события число благоприятствующих исходов М=1+5+100+1000=1106.

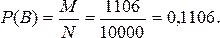
Событие «Покупатель не выиграет ни одного приза» - противоположное событию В: «Покупатель выиграл любой приз», поэтому обозначим его как `В. По формуле найдем:

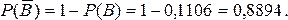
Ответ: а)0,0001; б )0,1106; в)0,8894.

Пример 2.Структура сотрудников в региональном отделении банка имеет следующий вид:

Женщины Мужчины
Администрация Операторы

Какова вероятность, что наудачу выбранный сотрудник окажется : а ) мужчина - администратор б) женщина – оператор в)Мужчина г) оператор ?

Решение. а) В банке работают 100 человек, N=100. Из них 15 – мужчин – администраторов , M =15.Следовательно, Р(мужчина-администратор) =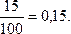

б) 35 сотрудников в банке – женщины – оператор. Следовательно, Р(женщина – оператор) =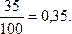

в)40 сотрудников в банке – мужчины. Следовательно, Р(мужчина) =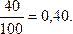

г) Из общего числа служащих в банке 60 – операторы, Следовательно,

Р(оператор) =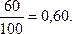

Ответ. а) 0,15 ; б) 0,35 ; в) 0,4; г) 0,6

studopedia.ru

Читайте также