Кривая
У этого термина существуют и другие значения, см. Кривая (значения).Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
Элементарная геометрия
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».
По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и некоторые трансцендентные кривые), применяя в каждом случае специальные приёмы.
Определение в топологии
Отображение отрезка
Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:
γ : [ a , b ] → X {\displaystyle \gamma :[a,b]\to X}При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [ a , b ] = [ 0 , 1 ] {\displaystyle [a,b]=[0,1]} , путями.
Отношение эквивалентности
Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые
γ 1 : [ a 1 , b 1 ] → X {\displaystyle \gamma _{1}:[a_{1},b_{1}]\to X} и γ 2 : [ a 2 , b 2 ] → X {\displaystyle \gamma _{2}:[a_{2},b_{2}]\to X}эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h {\displaystyle h} из отрезка [ a 1 , b 1 ] {\displaystyle [a_{1},b_{1}]} на отрезок [ a 2 , b 2 ] {\displaystyle [a_{2},b_{2}]} , такая что
γ 1 ≡ γ 2 ∘ h . {\displaystyle \gamma _{1}\equiv \gamma _{2}\circ h.}Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.
Комментарий
Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.
Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.
Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.
Кривая Жордана
 Кривая Жордана на плоскости с положительной мерой Лебега.
Кривая Жордана на плоскости с положительной мерой Лебега.
Кривой Жордана или простой кривой называется образ непрерывного инъективного отображения (вложения) окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой.
Известная теорема Жордана утверждает, что любая замкнутая кривая Жордана на плоскости делит её на «внутреннюю» и «внешнюю» часть.
Кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега, этот пример аналогичен кривой Пеано был построен Осгудом[1]. .
Определение в анализе
В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в R 2 {\displaystyle R^{2}} ). Пусть x ( t ) {\displaystyle x(t)} и y ( t ) {\displaystyle y(t)} — функции на отрезке [ a , b ] {\displaystyle [a,b]} , непрерывно дифференцируемые на этом отрезке, и такие, что ( x ′ ( t ) ) 2 + ( y ′ ( t ) ) 2 {\displaystyle (x'(t))^{2}+(y'(t))^{2}} ни для какого t не равно нулю. Тогда отображение γ : [ a , b ] → R 2 , t ↦ ( x ( t ) , y ( t ) ) {\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2},t\mapsto (x(t),y(t))} задаёт кривую, которая является гладкой; непараметризованная кривая называется гладкой, если она допускает такую параметризацию. Длину гладкой кривой можно вычислить по формуле
L ( γ ) = ∫ a b ( x ′ ( t ) ) 2 + ( y ′ ( t ) ) 2 d t . {\displaystyle {\text{L}}(\gamma )=\int _{a}^{b}{\sqrt {(x'(t))^{2}+(y'(t))^{2}}}\,dt.}Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.
Определение в дифференциальной геометрии
Основная статья: Дифференциальная геометрия кривыхЕсли X {\displaystyle X} — гладкое многообразие, можно определить гладкую кривую на X {\displaystyle X} как гладкое отображение γ : [ a , b ] → X {\displaystyle \gamma :[a,b]\to X} , дифференциал которого нигде не обращается в нуль. Если класс гладкости многообразия X {\displaystyle X} равен k {\displaystyle k} , то C k {\displaystyle C_{k}} -кривая вводится как кривая, для которой γ {\displaystyle \gamma } — k {\displaystyle k} раз непрерывно дифференцируемое отображение. Если X {\displaystyle X} — аналитическое многообразие (например, евклидово пространство) и γ {\displaystyle \gamma } — аналитическое отображение, кривую называют аналитической.
Гладкие кривые γ 1 : I → X {\displaystyle \gamma _{1}:I\to X} и γ 2 : J → X {\displaystyle \gamma _{2}:J\to X} называются эквивалентными, если существует диффеоморфизм p : I → J {\displaystyle p:I\to J} (замена параметра), такой что γ 1 = γ 2 ∘ p {\displaystyle \gamma _{1}=\gamma _{2}\circ p} . Классы эквивалентности по этому отношению называют непараметризованными гладкими кривыми.
Алгебраическая кривая
Основная статья: Алгебраическая криваяАлгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она назывется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x2 + y2 + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.
Алгебраические кривые можно определить и в пространствах большей размерности; они определяются как множество решений системы полиномиальных уравнений.
Любая плоская кривая может быть дополнена до кривой на проективной плоскости. Если плоская кривая определяется многочленом f(x, y) полной степени d, то многочлен
z d ⋅ f ( x / z , y / z ) {\displaystyle z^{d}\cdot f(x/z,y/z)}после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма xn + yn = zn в аффинной форме принимает вид xn + yn = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.
Часто встречающиеся примеры плоских кривых — коники (кривые второго порядка) и эллиптические кривые, имеющие важные приложения в криптографии. В качестве примеров алгебраических кривых, задаваемых уравнениями более высоких степеней, можно указать следующие:
- Кривые четвёртого порядка: лемниската Бернулли и овал Кассини.
- Кривые шестого порядка: астроида и нефроида.
- Кривая, определяемая уравнением произвольной чётной степени: (многофокусная) лемниската.
Трансцендентные кривые — это кривые, не являющиеся алгебраическими. Более точно, трансцендентные кривые — кривые, которые можно задать как линию уровня аналитической, но не алгебраической функции (или, в многомерном случае, системы функций). Примеры трансцендентных кривых:
- Синусоида
- Циклоида
- Спираль Архимеда
- Трактриса
- Цепная линия
- Гиперболическая спираль
Типы кривых
- Замкнутая кривая — кривая у которой начало совпадает с концом.
- Плоская кривая — кривая, все точки которой лежат в одной плоскости.
- Простая кривая — то же, что кривая Жордана.
- Путь — непрерывное отображение отрезка [ 0 , 1 ] {\displaystyle [0,1]} в топологическое пространство.
Типы точек на кривой
- Точка излома
- Касп
- Точка перегиба плоской кривой
- Двойная точка
Обобщённые кривые
Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:
Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.
Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L {\displaystyle L} , она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L ′ {\displaystyle L'} , гомеоморфное L {\displaystyle L} . Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.
Впоследствии это определение было обобщено Урысоном:
Кривой Урысона называется связное компактное топологическое пространство C {\displaystyle C} топологической размерности 1.
Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.
ru.wikipedia.org
Кривая это:
Кривая У этого термина существуют и другие значения, см. Кривая (значения).Кривая или линия — геометрическое понятие, определяемое в разных разделах геометрии различно.
Содержание
|
Элементарная геометрия
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки и иногда определяется как «длина без ширины» или как «граница фигуры». По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и также трансцендентные кривые), применяя в каждом случае специальные приёмы.
Параметрические определения
Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:
При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если , путями.
Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые
иэквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) из отрезка на отрезок , такая что
Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.
Кривая Жордана
Кривой Жордана называется образ непрерывного инъективного отображения окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой или простой дугой.
Следует отметить что кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега.
Комментарий
Существует большой соблазн определить кривую как образ непрерывного отображения отрезка в пространство.
Однако возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат, например, кривая Пеано. Более того, согласно теореме Мазуркевича, компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.
Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.
Аналитические кривые
Аналитическая кривая на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению , где является аналитической функцией. При этом на функцию накладываются ограничения, которые гарантируют, что
- это уравнение имеет бесконечное множество несовпадающих решений и
- это множество решений не заполняет «куска плоскости».
Аналогично определяются аналитические кривые в старших размерностях.
Алгебраические и трансцендентные кривые
Важный класс аналитических кривых составляют те, для которых функция есть многочлен от двух переменных. В этом случае кривая, определяемая уравнением , называется алгебраической, в противном случае — трансцендентной.
- Алгебраические кривые, задаваемые уравнением 1-й степени, суть прямые.
- Уравнение 2-й степени, имеющее бесконечное множество решений, определяет квадрики, то есть вырожденные и невырожденные конические сечения.
- Примеры кривых, задаваемых уравнениями 3-ей степени: циссоида Диокла, Декартов лист.
- Примеры кривых 4-ой степени: лемниската Бернулли и овал Кассини.
- Пример кривой 6-ой степени: астроида.
- Пример кривой, определяемой уравнением чётной степени: (многофокусная) лемниската.
Алгебраические кривые, определяемые уравнениями высших степеней, рассматриваются в алгебраической геометрии. При этом бо́льшую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебраическая кривая определяется уравнением вида
,где — однородный многочлен трех переменных, являющихся проективными координатами точек.
Более точно, трансцендентные кривые — кривые, которые можно задать через линию уровня аналитической функции (или, в многомерном случае, системы функций).
Примеры
- Синусоида,
- Циклоида,
- Спираль Архимеда,
- Трактриса,
- Цепная линия,
- Гиперболическая спираль
Типы кривых
- Замкнутая кривая — кривая у которой начало совпадает с концом.
- Плоская кривая — кривая, все точки которой лежат в одной плоскости.
- Простая кривая — то же, что кривая Жордана
- Путь — непрерывное отображение отрезка в топологическое пространство.
- Трансцендентная кривая
Типы точек на кривой
- Точка излома
- Точка перегиба плоской кривой
Обобщённые кривые
Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:
Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.
Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая , она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество , гомеоморфное . Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.
Впоследствии это определение было обобщено Урысоном:
Кривой Урысона называется связное компактное топологическое пространство топологической размерности 1.
Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.
См. также
- Дифференциальная геометрия кривых
- Кривая Урысона
- Кривые и их каустики
Литература
- Бураго Д. Ю., Бураго Ю. Д., Иванов С. В. Курс метрической геометрии НИЦ РХД, Институт компьютерных исследований, Инст-т компьют. исслед., Ин-т комп.исслед., ИКИ, , ISBN 5-93972-300-4, 2004
- Математический энциклопедический словарь. М. «Советская энциклопедия», 1988 г.
- Кривые // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки
 В Викисловаре есть статья «кривая»
В Викисловаре есть статья «кривая»
- Циклоидальные кривые
- Causticsангл.
- Surfaces, curvesангл.
|
Аналитическая • Жордана • Канторова • Урысона • Овал • Спрямляемая Радиус кривизны |
|
Эволюта • Эвольвента • Подера • Антиподера • Параллельная • Дуальная • Каустика |
|
Винтовая линия • Линия откоса • Локсодрома • Ортодромия • Губка |
|
Гипербола • Парабола • Эллипс (Окружность) |
|
Эллиптические: Эллиптическая кривая • Функции Якоби • Интеграл • Функции |
|
Бернулли (Овал Кассини) • Бута • Жероно |
|
Сплайн (B-сплайн • Кубический • Моносплайн • Эрмита) • Безье |
|
Кардиоида • Нефроида • Дельтоида • Астроида • Улитка Паскаля |
|
Архимедова (Ферма) • Гиперболическая • «Жезл» • Клотоида • Логарифмическая |
|
Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды) |
|
Квадратриса • Погони (Трактриса) • Трохоида • Цепная линия (перевёрнутая арочная) • Постоянной ширины • Синусоида |
|
Коха • Леви • Минковского • Пеано |
|
Салфетка + Ковёр Серпинского • Губка Менгера |
- Кривые
- Общая топология
- Метрическая геометрия
Wikimedia Foundation. 2010.
dic.academic.ru
ЛИНИЯ ВТОРОГО ПОРЯДКА это:
ЛИНИЯ ВТОРОГО ПОРЯДКАплоская линия, декартовы прямоугольные координаты к-рой удовлетворяют алгебраич. уравнению 2-й степени
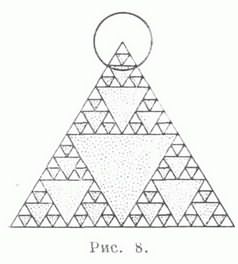

Уравнение (*) может и не определять действительного геометрич. образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат на нек-рый угол к одному из 9 приведенных ниже канонич. видов, каждому из к-рых соответствует определенный класс линий. Именно, нераспадающиеся линии:
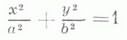
эллипсы,
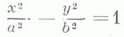
гиперболы,
у 2=2рх параболы,
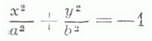
мнимые эллипсы;
распадающиеся линии:
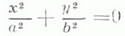
пары мнимых пересекающихся прямых,
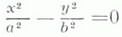
пары действительных пересекающихся
прямых,
х 2-a2=0 пары действительных параллельных прямых,
x2+а 2=0 пары мнимых параллельных прямых,
x2=0 пары совпадающих действительных прямых.
Л. в. п., имеющие единственный центр симметрии (центр Л. в. п.), наз. центральной линией. Координаты центра Л. в. п. определяются решением системы:
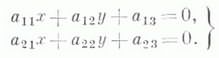
Л. в. п. без центра симметрии или снеопределенным центром наз. нецентральной линией.
Исследование вида Л. в. п. может быть проведено без приведения общего уравнения к канонич. виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов Л. в. п. - выражений, составленных из коэффициентов уравнения (*), значения к-рых не меняются при параллельном переносе и повороте системы координат 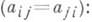
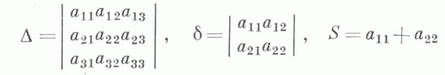
и семиинварианта (полуинварианта):
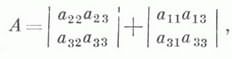
к-рый является инвариантом относительно поворота системы координат (см. табл.).
Многие важные свойства Л. в. п. могут быть изучены при помощи характеристической квадратичной формы
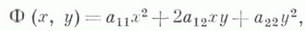
соответствующей уравнению (*). В частности, нераспадающаяся Л. в. п. оказывается эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости От того, будет ли Ф ( х, у).положительно определенной, отрицательно определенной, неопределенной или полуопределенной квадратичной формой, что устанавливается по корням ее характеристического уравнения:
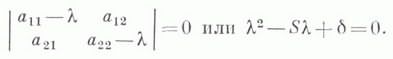
Три основных инварианта 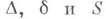 определяют Л. в. п. (кроме случая параллельных прямых) с точностью до движения евклидовой плоскости: если соответствующие инварианты
определяют Л. в. п. (кроме случая параллельных прямых) с точностью до движения евклидовой плоскости: если соответствующие инварианты  двух линий равны, то такие линии могут быть совмещены движением. Иными словами, эти линии эквивалентны по отношению к группе движений плоскости (метрически эквивалентны).
двух линий равны, то такие линии могут быть совмещены движением. Иными словами, эти линии эквивалентны по отношению к группе движений плоскости (метрически эквивалентны).
Существует классификация Л. в. п. с точки зрения других групп преобразований. Так, относительно более общей (чем группа движений) группы аффинных преобразований эквивалентными являются любые две линии, определяемые уравнениями одного канонич. вида. Напр., две подобные Л. в. п. считаются эквивалентными. Связи между различными аффинными классами Л. в. п. позволяет установить классификация с точки зрения проективной геометрии, в к-рой бесконечно удаленные элементы не играют особой роли. Действительные нераспадающиеся Л. в. п.: эллипсы, гиперболы и параболы образуют один проективный класс - класс действительных овальных линий (овалов). Действительная овальная линия является эллипсом, гиперболой или параболой в зависимости от того, как она расположена относительно бесконечно удаленной прямой: эллипс пересекает несобственную прямую в двух мнимых точках, гипербола - в двух различных действительных точках, парабола касается несобственной прямой; существуют проективные преобразования, переводящие эти линии одна в другую. Существует 5 классов проективной эквивалентности Л. в. п. Именно, невырождающиеся линии (x1 х 2, х 3 - однородные координаты):
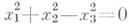 действительный овал,
действительный овал,  мнимый овал; вырождающиеся линии:
мнимый овал; вырождающиеся линии:
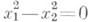 пара действительных прямых,
пара действительных прямых, 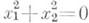 пара мнимых прямых,
пара мнимых прямых, 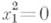 пара совпадающих прямых. Кроме аналитич. способа определения Л. в. п. (заданием уравнения) существуют и другие способы. Напр., эллипс, гипербола и парабола могут быть получены как сечения конич. поверхности плоскостью (см. Конические сечения).
пара совпадающих прямых. Кроме аналитич. способа определения Л. в. п. (заданием уравнения) существуют и другие способы. Напр., эллипс, гипербола и парабола могут быть получены как сечения конич. поверхности плоскостью (см. Конические сечения).
Исследование вида линий второго порядка с помощью инвариантов
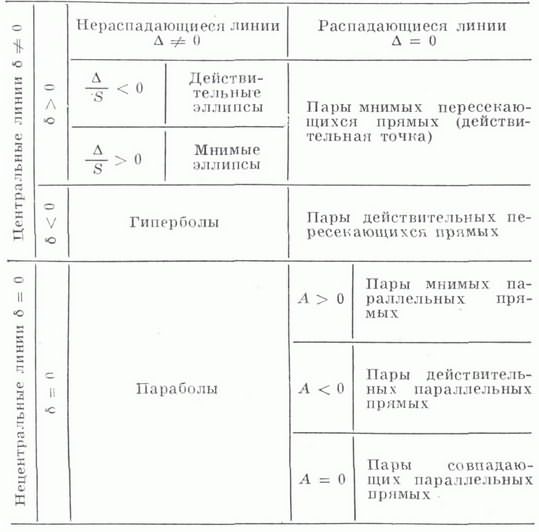
Лит.:[1] Александров П. С., Лекции по аналитической геометрии, М., 1968; [2J Ефимов Н. В., Краткий курс аналитической геометрии, 11 изд., М., 1972. А. Б. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Исходная линия
 Морские зоны в соответствии с Конвенцией ООН по морскому праву.
Морские зоны в соответствии с Конвенцией ООН по морскому праву.
Исходная линия — в морском праве, линия, от которой отсчитываются территориальные воды, прилежащая зона, исключительная экономическая зона и границы шельфа. Различают нормальную исходную линию, прямую исходную линию и исходную линию для архипелагов. Основным источником права, регулирующим определение исходной линии является Конвенция ООН по морскому праву.
Нормальная исходная линия
Нормальная исходная линия — это линия наибольшего отлива вдоль берега, указанная на официально признанных прибрежным государством морских картах крупного масштаба.
Прямая исходная линия
Если побережье сильно изрезано или береговая линия крайне непостоянна, могут быть выбраны определенные точки на берегу или на линии наибольшего отлива. Соединение этих точек даст прямую исходную линию, от которой будут отсчитываться различные зоны. Система прямых исходных линий не может применяться государством таким образом, чтобы территориальные воды другого государства оказались отрезанными от открытого моря или исключительной экономической зоны.
| Это заготовка статьи о праве и юриспруденции. Вы можете помочь проекту, дополнив её. |
|
История • Субъекты • Источники (Договор • Обычай • Прецедент • Общие принципы права • Доктрина) • Принципы • Нормы • Jus cogens • Erga omnes • Кодификация • Имплементация |
 |
|
|
Государства • Организации • Национально-освободительное движение • Суверенитет • Иммунитет • Правопреемство • Континуитет • Признание • Самоопределение • Нейтралитет |
||
правовой режим приобретение
|
||
гражданство правовой статус
|
||
|
Международных организаций • Прав человека • Дипломатическое • Консульское • Международных договоров • Морское • Воздушное • Космическое • Охраны окружающей среды • Экономическое • Мирное разрешение международных споров • Международной безопасности • Гуманитарное • Международной ответственности • Уголовное |
ru.wikipedia.org
 Акт определение
Акт определение Аренда определение
Аренда определение База данных определение
База данных определение Болезнь определение
Болезнь определение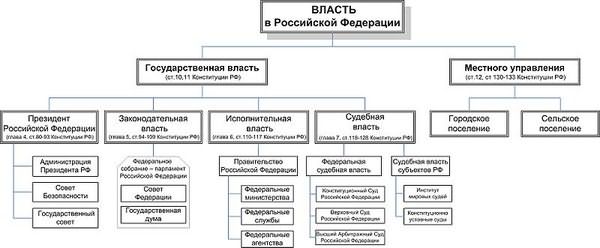 Власть определение
Власть определение Бетон определение
Бетон определение Генетические механизмы определения пола
Генетические механизмы определения пола Гражданская оборона определение
Гражданская оборона определение Груз определение
Груз определение Гражданское право определение
Гражданское право определение Гражданская война определение
Гражданская война определение