Понятие и свойства функции. Область определения и область значения
Основные данные о работе
| Версия шаблона | 2.1 |
| ЦДОР | |
| Вид работы | Творческое эссе |
| Название дисциплины | Математика (курс 13) |
| Тема | Понятие и свойства функции. Область определения и область значения. |
| Фамилия | |
| Имя | |
| Отчество | |
| № контракта |
Содержание
Понятие и свойства функции. Область определения и область значения……………3
Список использованных интернет-ресурсов…………………………………………...9
Основная часть
Понятие и свойства функции. Область определения и область значения
1.Фукция и её свойства.
Функция (отображение, оператор, преобразование) — это математическое понятие, отражающее связь между элементами множеств. Так же можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной однозначно определяет значение выражения, а значение месяца однозначно определяет значение следующего за ним месяца, а также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.
Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем в 1692 год. В свою очередь, Иоганн Бернулли в письме к Лейбницу употребил этот термин в смысле, более близком к современному.
Первоначально, понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, которое дал Эйлер в 1751 год, затем — Лакруа в 1806 год — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским в 1834 году и Дирихле в 1837 году.
К концу XIX века понятие функции переросло рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.
Функция – это одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Функция - это зависимость переменной у от переменной х, если каждому значению х соответствует единственное значение у.
Переменная х – это независимая переменная или аргумент.
Переменная у – это зависимая переменная.
Значение функции – это значение у, соответствующее заданному значению х.
Область определения функции – это все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- это все значения, которые принимает функция.
Функция является четной - если для любого х из области определения функции выполняется равенство f(х)=f(-х)
Функция является нечетной - если для любого х из области определения функции выполняется равенство f(-х)=-f(х)
Возрастающая функция - если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)
Убывающая функция - если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
2. Способы задания функции.
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее часто употребительным является способ задания функции с помощью формулы у=f(х), где f(х) – с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
На практике часто используется табличный способ задания функции. При данном способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами такого табличного задания функции являются: таблица квадратов и таблица кубов.
2. Виды функций и их свойства.
1) Постоянная функция- это функция, заданная формулой у=b, где b- это некоторое число.
Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат.
2) Прямая пропорциональность – это функция, заданная формулой у=kx, где к¹0. Число k называется коэффициентом пропорциональности.
Cвойства функции y=kx:
1. Область определения функции- множество всех действительных чисел;
2. y=kx - нечетная функция;
3. При k>0 функция возрастает, а при k
3)Линейная функция- это функция, которая задана формулой y=kx+b, где k и b- это действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b ; если b=0, то получаем прямую пропорциональность y=kx.
Свойства функции y=kx+b:
1. Область определения - множество всех действительных чисел;
2. Функция y=kx+b общего вида, т.е. ни четна, ни нечётна;
3. При k>0функция возрастает, а при k
Графиком функции является прямая.
4)Обратная пропорциональность – это функция, заданная формулой y=k/х, где k¹0.
Число k называют коэффициентом обратной пропорциональности.
Свойства функции y=k/x:
1. Область определения - множество всех действительных чисел кроме нуля;
2. y=k/x - нечетная функция;
3. Если k>0, то функция убывает на промежутке (0;+ ¥) и на промежутке (-;¥0). Если k
Графиком функции является гипербола.
5)Функция y=x2
Свойства функции y=x2:
1. Область определения - вся числовая прямая;
2. y=x2 - четная функция;
3. На промежутке [0;+¥) функция возрастает;
4. На промежутке (-¥;0] функция убывает.
Графиком функции является парабола.
6)Функция y=x3
Свойства функции y=x3:
1. Область определения - вся числовая прямая;
2. y=x3 - нечетная функция;
3. Функция возрастает на всей числовой прямой.
Графиком функции является кубическая парабола.
7)Степенная функция с натуральным показателем – это функция, заданная формулой y=xn, где n- натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x2; y=x3. Их свойства рассмотрены выше. Пусть n- это произвольное четное число, большее двух: 4,6,8... В этом случае функция y=xn обладает теми же свойствами, что и функция y=x2. График функции напоминает параболу y=x2, только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|
8)Степенная функция с целым отрицательным показателем – это функция, заданная формулой y=x-n, где n- натуральное число. При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4.
Пусть n- это нечетное число, большее единицы: 3,5,7... В этом случае функция y=x-n
обладает в основном теми же свойствами, что и функция y=1/х.
Пусть n- четное число, например n=2.
Свойства функции y=x-2:
1. Функция определена при всех x¹0;
2. y=x-2 - четная функция;
3. Функция убывает на (0;+¥) и возрастает на (-¥;0). Теми же свойствами обладают любые функции при четном n, большем двух.
9)Функция y=Öх
Свойства функции y=Öх:
1. Область определения - луч [0;+¥);
2. Функция y=Öх - общего вида;
3. Функция возрастает на луче [0;+¥).
10)Функция y=3Öх
Свойства функции y=3Öх:
1. Область определения- вся числовая прямая;
2. Функция y=3Öх нечетна;
3. Функция возрастает на всей числовой прямой.
11)Функция y=nÖх
При четном n функция обладает такими же свойствами, что и функция y=Öх.
При нечетном n функция y=nÖх обладает такими же свойствами, что и функция y=3Öх.
12)Степенная функция с положительным дробным показателем – это функция, заданная формулой y=xr, где r- это положительная несократимая дробь.
Свойства функции y=xr:
1.Область определения- луч [0;+¥);
2. Функция общего вида;
3. Функция возрастает на [0;+¥).
13) Степенная функция с отрицательным дробным показателем - функция, заданная формулой y=x-r, где r - это положительная несократимая дробь.
Свойства функции y=x-r:
1. Обл. определения - промежуток (0;+¥);
2. Функция общего вида;
3. Функция убывает на (0;+¥).
14)Обратная функция .
Если функция y=f(x) такова, что для любого ее значения yo уравнение f(x)=yo имеет относительно х единственный корень, то говорят, что функция f обратима.
Если функция y=f(x) определена и возрастает (убывает) на промежутке х и областью ее значений является промежуток у, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на у. Таким образом, чтобы построить график функции, обратной к функции y=f(x), нужно график функции y=f(x) подвергнуть преобразованию симметрии относительно прямой y=x.
15)Сложная функция- это функция, аргументом которой является другая любая функция. Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2. Получаем: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.
Понятие функции является одним из основных понятии математики. Оно не сразу возникло в таком виде, как мы им пользуемся сейчас, а как и другие фундаментальные понятия прошло длинный путь диалектического и исторического развития. Идея функциональной зависимости восходит к древнегреческой математике. Впервые термин "функция" ввел в рассмотрение знаменитый немецкий математик и философ Лейбниц в 1694 г. Однако, этот термин (определения он не дал вообще) он употребляет в узком смысле, понимая под функцией изменение ординаты кривой в зависимости от изменения ее абсциссы. Таким образом, понятие функции носит у Лейбница "геометрический налет". Ученик Лейбница, Иоганн Бернулли пошел дальше своего учителя. Он дал более общее определение функции, освобождая последнее от геометрических представлений и терминов: "функцией переменной величины называется количество, образованное каким угодно способом из этой величины и постоянных".
studopedia.ru
Область определения функции
Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Определение
Если на множестве X {\displaystyle X} задана функция, которая отображает множество X {\displaystyle X} в другое множество, то множество X {\displaystyle X} называется областью определения или областью задания функции.
Более формально, если задана функция f {\displaystyle f} , которая отображает множество X {\displaystyle X} в Y {\displaystyle Y} , то есть: f : X → Y {\displaystyle f\colon X\to Y} , то
- множество X {\displaystyle X} называется областью определения[1] или областью задания[2] функции f {\displaystyle f} и обозначается D ( f ) {\displaystyle D(f)} или d o m f {\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).
Иногда рассматривают функции, определенные на подмножестве D {\displaystyle D} некоторого множества X {\displaystyle X} . В этом случае множество X {\displaystyle X} иногда называют областью отправления функции f {\displaystyle f} [3].
Примеры
Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.
Числовые функции
Числовые функции — это функции, относящиеся к следующим двум классам:
- вещественнозначные функции вещественного переменного — это функции вида f : R → R {\displaystyle f\colon \mathbb {R} \to \mathbb {R} } ;
- а также комплекснозначные функции комплексного переменного вида f : C → C {\displaystyle f\colon \mathbb {C} \to \mathbb {C} } ,
где R {\displaystyle \mathbb {R} } и C {\displaystyle \mathbb {C} } — множества вещественных и комплексных чисел соответственно.
Тождественное отображение
Область определения функции f ( x ) = x {\displaystyle f(x)=x} совпадает с областью отправления ( R {\displaystyle \mathbb {R} } или C {\displaystyle \mathbb {C} } ).
Гармоническая функция
Область определения функции f ( x ) = 1 / x {\displaystyle f(x)=1/x} представляет собой комплексную плоскость без нуля:
d o m f = C ∖ { 0 } {\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}} ,поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.
Дробно-рациональные функции
Область определения функции вида
f ( x ) = a 0 + a 1 x + ⋯ + a m x m b 0 + b 1 x + ⋯ + b n x n {\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}}представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения
b 0 + b 1 x + ⋯ + b n x n = 0 {\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0} .Эти точки называются полюсами функции f {\displaystyle f} .
Так, например, f ( x ) = 2 x x 2 − 4 {\displaystyle f(x)={\frac {2x}{x^{2}-4}}} определен на всех точках, где знаменатель не обращается в ноль, то есть, где x 2 − 4 ≠ 0 {\displaystyle x^{2}-4\neq 0} . Таким образом d o m f {\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и -2.
Мера
Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.
Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.
Например, определённый интеграл представляет собой функцию ориентированного промежутка.
Функционал
Пусть F = { f ∣ f : X → R } {\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}} — семейство отображений из множества X {\displaystyle X} в множество R {\displaystyle \mathbb {R} } . Тогда можно определить отображение вида F : F → R {\displaystyle F\colon \mathbb {F} \to \mathbb {R} } . Такое отображение называется функционалом.
Если, например, фиксировать некоторую точку x 0 ∈ X {\displaystyle x_{0}\in ~X} , то можно определить функцию F ( f ) = f ( x 0 ) {\displaystyle F(f)=f(x_{0})} , которая принимает в «точке» f {\displaystyle f} то же значение, что и сама функция f {\displaystyle f} в точке x 0 {\displaystyle x_{0}} .
ru.wikipedia.org
§8. Числовая функция. Область определения и область значений функции
Рассмотрим числовые функции, т.е. функции, область определения и область значения которых – числовые множества.
Определение. Пусть Xи Y– некоторые числовые множества (XR, YR). Числовой функцией называется такое соответствие между элементами множеств Xи Y, при котором каждому числу х из множества Xсоответствуетне более одногочисла у из множества Y.
Функции принято обозначать буквами: f,q,h, и др. В общем случае, элемент y Y, соответствующий элементу x A, называется значением функции fи записывается так: y= f(x).
Сложилась традиция переменную x называть аргументом функции.
Например, X = {1, 2, 3, 4, 5, 6}, Y= {5, 6, 8, 9, 10, 11, 12}. Соответствие f: « х меньше y на 4». Каждому x Î X соответствует не более одного yÎY(y=4 + x): 1 ® 5; 2 ® 6; 4 ® 8, 5 ® 9; 6 ® 10, поэтому это соответствие функция.
Из множества X выделим подмножество тех элементов х, для которых есть соответствующий элемент во множестве У . Это множество называют областью (или множеством) определения функции. Его обозначают D(f). В нашем примере D(f) = {1, 2, 4, 5, 6}. Множество всех элементов y Y, которые являются значениями функции f, называются множеством (областью) значений функции (E(f)).
В нашем примере E(f) = {5, 6, 8, 9, 10}.
С учетом этого можно дать другое определение функции.
Определение. Пусть Xи Y– некоторые числовые множества (XÍR, YÍR). Числовой функцией, определенной на Xи принимающей значения из Y, называется такое соответствие f, при котором каждому числу xÎXсоответствует единственное число yÎY.
Например, A= {a a N 1 a 8}, B= {3, 5}, соответствие : «а делится на b ».
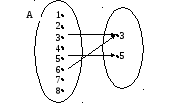
В
Так как каждому a A соответствует не более одного b B , то это соответствие – функция.
Так как числовая функция – частный случай соответствия, то все способы задания соответствия являются и способами задания функции.
Вспомним их:
1) задание числовой функции путём перечисления всех пар элементов, которые находятся в данном соответствии. Если область определения функции – конечное множество, число элементов которого не очень велико, то такую функцию можно задать путем перечисления всех пар соответственных элементов.
Отношение q, заданное перечислением пар, является функцией, если оно не содержит двух разных пар с одинаковыми первыми элементами.
б) задание числовой функции графом.
Соответствие j в примере 2 задано графом.
Соответствие, заданное графом, является функцией, если граф не содержит двух разных стрелок с общим началом.
в) графический способ задания числовой функции.
Если функция задана перечислением пар, то в декартовой системе координат каждую пару можно изобразить точкой. Множество построенных точек и называют графиком функции. Построим график функции q.
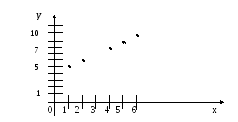




График соответствия, которое является функцией, не содержит двух разных точек с одинаковой абсциссой.
г) задание числовой функции указанием характеристического свойства.
Примерами являются примеры 1, 2.
Частный случай: задание числовой функции формулой.
Если область определения функции, заданной формулой, явно не указана и нет каких-либо дополнительных ограничений, то считают, что функция определена на множестве всех тех значений аргумента, при которых все указанные в формуле операции выполнимы.
Например, характеристическое свойство в примере 1 можно записать в виде уравнения с двумя переменными:
у = 4 + х, т.е. в виде формулы.
От одного способа задания функции можно переходить к другому.
StudFiles.ru
Как найти область определения функции и область значения??? приведите пример и опишите подробнее пожалуйста
Маря
Каждая функция содержит два типа переменных: независимую переменную и зависимую переменную. Например, в функции y = f(x) = 2x + y «х» является независимой переменной, а «у» - зависимой переменной. Область определения функции - это множество чисел, на котором задается функция (другими словами, это те значения «х», которые можно подставить в данное уравнение). Область значений функции – все значения, которые принимает функция в ее области определения (другими словами, это те значения «у», которые вы получаете при подста
Если функция задана дробным выражением, найдите корни выражения, стоящего в знаменателе. Для этого приравняйте выражение, стоящее в знаменателе, к нулю и найдите «х».
1,Пример: дана функция е (х) = х + 5 / х - 2. Эта функция задана дробным выражением. Найдите корни выражения в знаменателе: х – 2 = 0; х = 2.новке всех возможных значений «х»).
2.
Запишите область определения функции. После нахождения корней выражения в знаменателе запишите область определения функции в математической форме.
В нашем примере знаменатель равен 0 при х = 2, следовательно х не может принимать значение 2 (так как на 0 делить нельзя). Область определения запишется в следующем виде: (-∞; 2)U(2; +∞).
Читается так: от минус бесконечности до двух и от двух до плюс бесконечности.
3.Нарисуйте координатную плоскость: проведите ось Х (горизонтально) и ось Y (вертикально).
4.
На осях координат нанесите числовые отметки (через равные промежутки).
5.Найдите точки графика. Для этого подставьте в данную функцию значения «х» (из области определения функции) и найдите значения «у».
В нашем примере подставьте любые значения «х», кроме 2, так как 2 исключена из области определения.
6.Отложите точки на координатной плоскости. Затем соедините их плавной линией.
7.
Найдите область значений функции. Для этого на координатной плоскости найдите такую горизонтальную прямую, которая не пересекается с графиком функции. Точка пересечения этой прямой и оси Y будет исключена из области значений функции.
В нашем примере прямая, заданная функцией у = 1, не пересекает график исходной функции. Следовательно «у» не принимает значение 1 и оно исключается из области значений функции. Математически область значений записывается так:
(-∞,1)U(1,+∞)
Читается так: от минус бесконечности до единицы и от единицы до плюс бесконечности.
Лира
Область определения функции это то множество значений, которые может принимать аргумент функции. Например, для y(x)=x/x-1 ООФ будет интервал от минус бесконечности до 1 и от 1 до плюс бесконечности (х не равно 1). Область значения функции это то множество значений, которое может принимать функция. Например, для y(x)=sin(x) ОЗФ это отрезок от -1 до 1.
Как найти область значения и область определения фунции?
Jenny
область значения смотри по графику по оси Оу, а область определения-по оси Ох
если без графика, то область значения зависит от функции (например Cos и Sin всгда от -1 до 1,и т д), а область определения там может от ОДЗ зависеть или ограничений (если дробь, то знаменатель не равен нулю)
Leonid
Область определения - это такие значения аргумента, при которых может существовать функция. Скажем, если есть квадратный корень - то под ним должно стоять неотрицательное выражение. Если есть логарифм - то строго положительное. Если есть знаменатель - то он не должен быть равен нулю, а если тангенс - то то, что под ним, не должно быть равно пи пополам (плюс-минус произвольное число пи) . И так далее. То есть нужно смореть на всякие такие вещи, которые могут НЕ существовать при некоторых значениях арггумента.
А область значений (тут множественное число принято употреблять) - это всё, что между максимум и минимумом функции. И тут уже надо исследовать вид конкретной функции.
Читайте также
![Область значения Область значения]() Область значения
Область значения- Как найти область определения функции
![Как найти область значения функции Как найти область значения функции]() Как найти область значения функции
Как найти область значения функции![Функции нескольких переменных область определения линии уровня Функции нескольких переменных область определения линии уровня]() Функции нескольких переменных область определения линии уровня
Функции нескольких переменных область определения линии уровня![Как обозначается область определения функции Как обозначается область определения функции]() Как обозначается область определения функции
Как обозначается область определения функции![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![1515 На часах значение 1515 На часах значение]() 1515 На часах значение
1515 На часах значение![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия![16 16 Значение времени 16 16 Значение времени]() 16 16 Значение времени
16 16 Значение времени![Семен значение имени характер и судьба Семен значение имени характер и судьба]() Семен значение имени характер и судьба
Семен значение имени характер и судьба![15 15 Значение 15 15 Значение]() 15 15 Значение
15 15 Значение
 Область значения
Область значения Как найти область значения функции
Как найти область значения функции Функции нескольких переменных область определения линии уровня
Функции нескольких переменных область определения линии уровня Как обозначается область определения функции
Как обозначается область определения функции Аутентичность значение слова
Аутентичность значение слова 1515 На часах значение
1515 На часах значение Чувак значение слова с еврейского
Чувак значение слова с еврейского Барыга значение слова википедия
Барыга значение слова википедия 16 16 Значение времени
16 16 Значение времени Семен значение имени характер и судьба
Семен значение имени характер и судьба 15 15 Значение
15 15 Значение