Отрезок это:
Отрезок
Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе. Отрезок — множество точек, которое обычно изображается ограниченной частью прямой.
Содержание
|
Отрезок в геометрии
Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. При этом сама точка в геометрии является абстрактным объектом, не имеющим никакой длины и вообще каких-либо измеряемых характеристик. Отрезок прямой, соединяющий две точки и (которые называются концами отрезка), обозначается следующим образом — . Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок ». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как .
Отрезок числовой прямой
Отрезок числовой (координатной) прямой (числовой отрезок, сегмент) — множество вещественных чисел , удовлетворяющих неравенству , где заранее заданные вещественные числа и , удовлетворяющие неравенству :
.Любой отрезок заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.
Число называется длиной числового отрезка .
Стягивающаяся система сегментов
Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой .
Система сегментов обозначается . Подразумевается, что каждому натуральному числу поставлен в соответствие отрезок .
Система сегментов называется стягивающейся, если[2]
- каждый следующий отрезок содержится в предыдущем;
- соответствующая последовательность длин отрезков бесконечно мала.
У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.
Этот факт следует из свойств монотонной последовательности.
Направленный отрезок
Основная статья: Вектор (математика)Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки и представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.
Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
Примечания
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 53. — 672 с. — ISBN 5-482-00445-7
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 68 — 105. — 672 с. — ISBN 5-482-00445-7
См. также
- Интервал
- Промежуток
- Алгоритмы построения отрезка
- Прямая
- Евклидова геометрия
- Элементарная математика
Wikimedia Foundation. 2010.
dic.academic.ru
Середина отрезка
 Средняя точка отрезка с вершинами (x1, y1) и (x2, y2)
Средняя точка отрезка с вершинами (x1, y1) и (x2, y2)
Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих его концов отрезка. Является центром масс как всего отрезка, так и его конечных точек.
Координаты
Средняя точка отрезка в n {\displaystyle n} -мерном пространстве, концами которого являются точки A = ( a 1 , a 2 , … , a n ) {\displaystyle A=(a_{1},a_{2},\dots ,a_{n})} и B = ( b 1 , b 2 , … , b n ) {\displaystyle B=(b_{1},b_{2},\dots ,b_{n})} , задаётся формулой:
A + B 2 {\displaystyle {\frac {A+B}{2}}} .Таким образом, i {\displaystyle i} -я координата средней точки ( i = 1 , 2 , … , n {\displaystyle i=1,2,\dots ,n} ) равна:
a i + b i 2 {\displaystyle {\frac {a_{i}+b_{i}}{2}}} .Построение
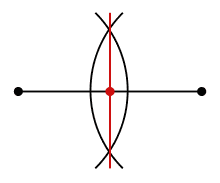 Построение с помощью циркуля и линейки
Построение с помощью циркуля и линейки
Если заданы две точки, нахождение середины образованного ими отрезка может быть осуществлено с помощью циркуля и линейки. Для нахождения середины отрезка на плоскости можно сначала построить две дуги равного (и достаточно большого) радиуса с центрами в концах отрезка, а затем через точки пересечения этих дуг провести прямую. Точка, где полученная прямая пересекает отрезок, является его серединой.
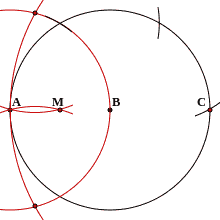 Построение с помощью одного циркуля
Построение с помощью одного циркуля
С использованием теоремы Мора — Маскерони возможно также нахождение середины отрезка с помощью одного только циркуля: на первом шаге для отрезка ( A B ) {\displaystyle (AB)} строится точка C {\displaystyle C} , симметричная точке A {\displaystyle A} относительно точки B {\displaystyle B} ; на втором шаге строится инверсия точки C {\displaystyle C} относительно окружности радиуса | A B | \displaystyle с центром в точке A {\displaystyle A} ; полученная точка является серединой отрезка ( A B ) {\displaystyle (AB)} [1][2][3].
Можно также построить середину отрезка с помощью только линейки при условии, что на плоскости имеется окружность с отмеченным центром[4].
Геометрические свойства
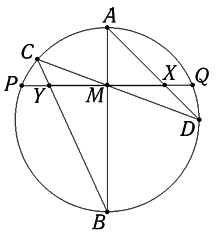
Середина любого диаметра окружности является центром окружности. Перпендикуляр к любой хорде, проходящий через её середину, проходит через центр окружности. Теорема о бабочке утверждает, что если M {\displaystyle M} является серединой хорды P Q {\displaystyle PQ} и через середину проходят две другие хорды A B {\displaystyle AB} и C D {\displaystyle CD} , то A D {\displaystyle AD} и B C {\displaystyle BC} пересекают хорду P Q {\displaystyle PQ} в точках X {\displaystyle X} и Y {\displaystyle Y} соответственно таким образом, что M {\displaystyle M} является серединой отрезка X Y {\displaystyle XY} .
Центр эллипса является серединой отрезка, соединяющего два фокуса[en] эллипса.
Середина отрезка, соединяющего вершины гиперболы, является центром гиперболы.
Перпендикуляры к серединам сторон треугольника пересекаются в одной точке, и эта точка является центром описанной окружности. Центр девяти точек треугольника — середина отрезка, соединяющего центра описанной окружности с ортоцентром данного треугольника. Вершины серединного треугольника данного треугольника лежат в серединах сторон треугольника.
В прямоугольном треугольнике центр описанной окружности является серединой гипотенузы. В равнобедренном треугольнике медиана, высота и биссектриса угла при вершине совпадают с прямой Эйлера и осью симметрии, и эта прямая проходит через середину основания.
Две бимедианы выпуклого четырёхугольника — это отрезки, соединяющие середины противоположных сторон. Две бимедианы и отрезок, соединяющий середины диагоналей, пересекаются в одной точке, которая является серединой этих трёх отрезков[5]. Теорема Брахмагупты утверждает, что если вписанный в окружность четырёхугольник является ортодиагональным (то есть, имеющий перпендикулярные диагонали), то перпендикуляры к сторонам из точки пересечения диагоналей всегда проходят через середину противоположной стороны. Теорема Вариньона утверждает, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма, а если четырёхугольник к тому же является самонепересекающимся, то площадь параллелограмма равна половине площади четырёхугольника. Прямая Ньютона — линия, соединяющая середины двух диагоналей выпуклого четырёхугольника, не являющегося параллелограммом. Отрезки, соединяющие середины противоположных сторон выпуклого четырёхугольника, пересекаются в точке, лежащей на прямой Ньютона.
Правильный многоугольник имеет вписанную окружность, которая касается всех сторон многоугольника в серединах его сторон. В правильном многоугольнике с чётным числом сторон середины диагоналей, соединяющих противоположные центры, являются центром многоугольника. Серединный многоугольник — многоугольник, вершины которого — середины рёбер исходного многоугольника. Растянутый многоугольник серединных точек вписанного многоугольника P является другим вписанным многоугольником, вписанным в ту же окружность, и его вершины являются серединами дуг между вершинами P[6]. Повторение операции создания многоугольника растянутых средних точек приводит к последовательности многоугольников, форма которых сходится к правильному многоугольнику[6][7].
Обобщения
Середина отрезка является аффинным инвариантом, поэтому координатные формулы[⇨] применимы к любой аффинной системе координат.
Середину отрезка невозможно определить в проективной геометрии: любая внутренняя точка отрезка может быть проективно отображена в любую другую точку внутри (того же или любого другого) проективного отрезка. Закрепление одной такой точки в качестве середины определяет аффинную структуру на проективной прямой, содержащей этот отрезок. Четвёртая точка гармонической четвёрки для такой «средней точки» и двух конечных точек является бесконечно удалённой точкой[8].
Понятие середины отрезка можно ввести на геодезических в римановом многообразии, но в отличие от аффинного случая, середина отрезка может быть не единственной.
ru.wikipedia.org
3.4. Определение натуральной величины отрезка
Если отрезок прямой занимает общее положение, то определить истинную величину прямой на плоскостях проекций нельзя. Поэтому для определения длины отрезка по его проекциям используют способ прямоугольного треугольника: длина отрезка измеряется гипотенузой прямоугольного треугольника, одним катетом которого является проекция отрезка на плоскость, а другим – разность расстояний концов его до этой плоскости. Рассмотрим прямую общего положения в пространстве.
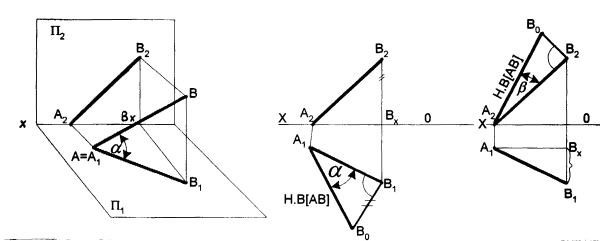
Рис. 9
Треугольник АВВ1–прямоугольный. Гипотенуза АВ является натуральной длиной отрезка (рис. 9, а), а проекция А1В1– катетом. Второй катет ВВ1определяет превышение одного конца отрезка над другим относительно плоскости проекций П1и проецируется без искажения на фронтальную плоскость проекций П2. Угол= ВАВ1– это угол наклона прямой АВ к горизонтальной плоскости проекций.
Построения см. на рис. 9, б. Из точки В1 проведём перпендикуляр к проекции А1В1, отложим на нём отрезок В1Во= ВхВ2и соединим прямой точки А1и Во. Построенный треугольник А1ВоВ1= АВВ1(рис. 9, а), так как равны их катеты и угол между ними составляет 90°. Следовательно, отрезок А1Во равен отрезку АВ и угол В1А1Воопределяет угол наклона отрезка АВ к горизонтальной плоскости проекций.
Аналогичное построение можно сделать на фронтальной плоскости проекций, только в качестве второго катета нужно будет взять разность глубин его концов В1Вх(рис. 9, в).
Определение длины отрезка с использованием способа замены плоскостей проекций будем рассматривать в вузе.
Вопросы для самопроверки
1. Какое положение может занимать прямая относительно плоскостей проекций ?
2. Прямая общего положения (начертить комплексный чертёж).
3. В каком случае прямая обращается в точку и как называются такие прямые ? Привести пример.
4. Какие точки называются конкурирующими ?
5. Сформулировать признак принадлежности точки, прямой (см. выше).
6. Сформулировать правило прямоугольного треугольника.
4. Плоскость
Плоскость может быть задана аналитически (уравнением) или графически (проекциями). Для графического задания плоскости достаточно построить проекции определяющих её элементов (рис. 10):
1) трёх точек, не лежащих на одной прямой;
2) прямой и точки, не лежащей на этой прямой;
3) двух пересекающихся прямых;
4) двух параллельных прямых;
5) любой плоской фигурой.

Рис. 10
В зависимости от положения плоскости относительно плоскостей проекций различают плоскости общего и частного положения.
Плоскость, не перпендикулярную ни одной из основных плоскостей проекций называют плоскостью общего положения (рис. 10.5).
Плоскости частного положения можно разделить на две группы:
проецирующие и плоскости уровня.
4.1. Проецирующие плоскости
Проецирующие плоскости– это плоскости, перпендикулярные к одной из плоскостей проекций (рис. 11). К ним относятся:
1) горизонтально-проецирующая П1;
2) фронтально-проецирующая П2;
3) профильно-проецирующая П3.
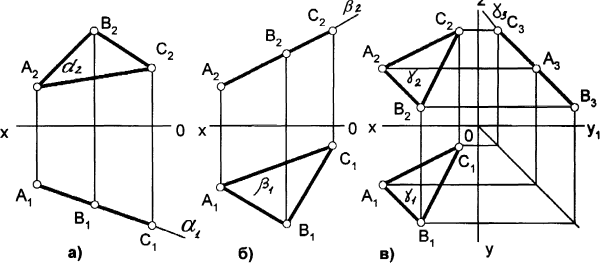
Рис. 11
Отличительной особенностью проецирующих плоскостей является то, что все геометрические образы, принадлежащие проецирующей плоскости, проецируются на перпендикулярную к ней плоскость в одну прямую, совпадая с главной проекцией (следом):
горизонтально-проецирующая плоскость А1В1С1(рис. 11, а),
фронтально-проецирующая плоскость А2В2С2(рис. 11, б),
профильно-проецирующая плоскость А3В3С3(рис. 11, в).
StudFiles.ru
Что такое отрезок?
Sнежн@я kоролев@
Отрезком называется часть прямой, которая содержит две разные точки A и B этой прямой (концы отрезка) и все точки прямой, которые лежат между ними (внутренние точки отрезка) .
Отрезок прямой — это множество (часть прямой) , состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки A и B (которые называются концами отрезка) , обозначается следующим образом — [A;B]. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок AB». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как |AB|.
Для обозначения отрезка с концами в точках A и B будем использовать символ [AB].
О точке b, принадлежащей отрезку AB, говорят также, что точка b лежит между точками A и B (если b – внутренняя точка отрезка) , а также, что отрезок AB содержит точку b..
Читайте также
![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Генетическое определение пола кратко Генетическое определение пола кратко]() Генетическое определение пола кратко
Генетическое определение пола кратко![Генетические механизмы определения пола Генетические механизмы определения пола]() Генетические механизмы определения пола
Генетические механизмы определения пола![Акт определение Акт определение]() Акт определение
Акт определение![Легальное определение юридического лица дано Легальное определение юридического лица дано]() Легальное определение юридического лица дано
Легальное определение юридического лица дано![Определение высоты объекта Определение высоты объекта]() Определение высоты объекта
Определение высоты объекта![Дайте определение понятию авария Дайте определение понятию авария]() Дайте определение понятию авария
Дайте определение понятию авария![Деталь определение Деталь определение]() Деталь определение
Деталь определение![Закон джоуля ленца формула и определение Закон джоуля ленца формула и определение]() Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение![Двигатель определение Двигатель определение]() Двигатель определение
Двигатель определение- Дать определение понятию индустриализация
![Машина определение Машина определение]() Машина определение
Машина определение
 Болезнь определение
Болезнь определение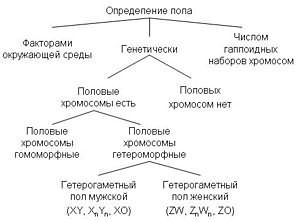 Генетическое определение пола кратко
Генетическое определение пола кратко Генетические механизмы определения пола
Генетические механизмы определения пола Акт определение
Акт определение Легальное определение юридического лица дано
Легальное определение юридического лица дано Определение высоты объекта
Определение высоты объекта Дайте определение понятию авария
Дайте определение понятию авария Деталь определение
Деталь определение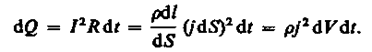 Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение Двигатель определение
Двигатель определение Машина определение
Машина определение