Пространство в физике
| Возможно, эта статья содержит оригинальное исследование. Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление. Дополнительные сведения могут быть на странице обсуждения. (31 августа 2015) |
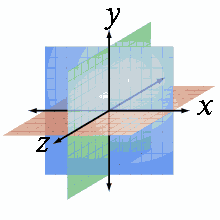
В физике термин пространство понимают, в основном, в двух смыслах[источник не указан 703 дня]:
- так называемое обычное пространство, называемое также физическим пространством[1] — трёхмерное пространство нашего повседневного мира и/или прямое развитие этого понятия в физике (развитие, возможно, иногда достаточно изощрённое, но прямое, так что можно сказать: наше обычное пространство на самом деле таково). Это пространство, в котором определяется положение физических тел, в котором происходит механическое движение, геометрическое перемещение различных физических тел и объектов.
- различные абстрактные пространства в том смысле, как они понимаются в математике, не имеющие к обычному («физическому») пространству никакого отношения, кроме отношения более или менее далёкой формальной аналогии (иногда, в отдельных простых случаях, правда, просматривается и генетическая связь, например для пространства скоростей, импульсного пространства). Обычно это те или иные абстрактные векторные или линейные пространства, впрочем, часто снабженные разнообразными дополнительными математическими структурами. Как правило, в физике термин пространство применяется в этом смысле обязательно с уточняющим определением или дополнением (пространство скоростей, цветовое пространство, пространство состояний, гильбертово пространство, пространство спиноров), или, в крайнем случае, в виде неразрывного словосочетания абстрактное пространство. Такие пространства используются однако для постановки и решения вполне «земных» задач в обыкновенном трёхмерном пространстве.
Рассматриваются в физике и ряд пространств, которые занимают как бы промежуточное положение в этой простой классификации, то есть такие, которые в частном случае могут совпадать с обычным физическим пространством, но в общем случае — отличаться от него (как, например, конфигурационное пространство) или содержать обычное пространство в качестве подпространства (как фазовое пространство, пространство-время или пространство Калуцы).
В теории относительности в её стандартной интерпретации пространство[2] оказывается одним из проявлений единого пространства-времени, и выбор координат в пространстве-времени, в том числе и разделение их на пространственные и временную, зависит от выбора конкретной системы отсчёта[3]. В общей теории относительности (и большинстве других метрических теорий гравитации) в качестве пространства-времени рассматривается псевдориманово многообразие (или, для альтернативных теорий, даже что-то более общее) — более сложный объект, чем плоское пространство, которое может играть роль физического пространства в большинстве других физических теорий (впрочем, практически у всех общепринятых современных теорий есть или подразумевается форма, обобщающая их на случай псевдориманова пространства-времени общей теории относительности, являющейся непременным элементом современной стандартной фундаментальной картины).
В большинстве разделов физики сами свойства физического пространства (размерность, неограниченность и т. п.) никак не зависят от присутствия или отсутствия материальных тел. В общей теории относительности оказывается, что материальные тела модифицируют свойства пространства, а точнее, пространства-времени, «искривляют» пространство-время.
Одним из постулатов любой физической теории (Ньютона, ОТО и т. д.) является постулат о реальности того или иного математического пространства (например, Евклидова у Ньютона).
Конечно же, различные абстрактные пространства (в чисто математическом понимании термина пространство) рассматриваются не только в фундаментальной физике, но и в разных феноменологических физических теориях, относящихся к разным областям, а также на стыке наук (где разнообразие способов применения этих пространств достаточно велико). Иногда случается, что название математического пространства, используемого в прикладных науках, берут в фундаментальной физике для обозначения некоего абстрактного пространства фундаментальной теории, которое оказывается похоже на него некоторыми формальными свойствами, что дает термину и понятию больше живости и (абстрактной) наглядности, приближает хоть как-то немного к повседневному опыту, «популяризирует» его. Так было, например, сделано в отношении упомянутому выше внутреннего пространства заряда сильного взаимодействия в квантовой хромодинамике, которое назвали цветовым пространством потому, что оно чем-то напоминает цветовое пространство в теории зрения и полиграфии.
ru.wikipedia.org
Пространство в физике это:
Пространство в физике У этого термина существуют и другие значения, см. Пространство.В физике термин пространство понимают, в основном, в двух смыслах:
1) так называемое обычное пространство, называемое также физическим пространством[1] — трехмерное пространство нашего повседневного мира и/или прямое развитие этого понятия в физике (развитие, возможно, иногда достаточно изощренное, но прямое, так что можно сказать: наше обычное пространство на самом деле таково). Это пространство, в котором определяется положение физических тел, в котором происходит механическое движение, геометрическое перемещение различных физических тел и объектов. 2) различные абстрактные пространства в том смысле, как они понимаются в математике, не имеющие к обычному («физическому») пространству никакого отношения, кроме отношения более или менее далекой формальной аналогии (иногда, в отдельных простых случаях, правда, просматривается и генетическая связь, например для пространства скоростей, импульсного пространства). Обычно это те или иные абстрактные векторные или линейные пространства, впрочем, часто снабженные разнообразными дополнительными математическими структурами. Как правило, в физике термин пространство применяется в этом смысле обязательно с уточняющим определением или дополнением (пространство скоростей, цветовое пространство, пространство состояний, гильбертово пространство, пространство спиноров), или, в крайнем случае, в виде неразрывного словосочетания абстрактное пространство. Такие пространства используются однако для постановки и решения вполне «земных» задач в обыкновенном трёхмерном пространстве.Рассматриваются в физике и ряд пространств, которые занимают как бы промежуточное положение в этой простой классификации, то есть такие, которые в частном случае могут совпадать с обычным физическим пространством, но в общем случае — отличаться от него (как, например, конфигурационное пространство) или содержать обычное пространство в качестве подпространства (как фазовое пространство, пространство-время или пространство Калуцы).
В теории относительности в ее стандартной интерпретации пространство[2] оказывается одним из проявлений единого пространства-времени, и выбор координат в пространстве-времени, в том числе и разделение их на пространственные и временную, зависит от выбора конкретной системы отсчёта.[3]
В большинстве разделов физики сами свойства физического пространства (размерность, неограниченность и т. п.) никак не зависят от присутствия или отсутствия материальных тел. В общей теории относительности оказывается, что материальные тела модифицируют свойства пространства, а точнее, пространства-времени, «искривляют» пространство-время.
Одним из постулатов любой физической теории (Ньютона, ОТО и т. д.) является постулат о реальности того или иного математического пространства (например, Евклидова у Ньютона).
См. также
- Размерность пространства
Примечания
- ↑ Физическое пространство — это уточняющий термин, используемый для разграничения этого понятия как от более абстрактного (обозначаемого в этой оппозиции как абстрактное пространство), так и для различения реального пространства от слишком упрощенных его математических моделей.
- ↑ Тут имеется в виду трехмерное «обычное пространство», т.е. пространство в понимании (1), как описано в начале статьи. В традиционных рамках теории относительности стандартным является именно такое употребление термина (а для четырехмерного пространства Минковского или четырехмерного псевдориманова многообразия общей теории относительности используется соответственно термин пространство-время). Однако в более новых работах, особенно если это не может вызвать путаницы, термин пространство употребляют и в отношении пространства-времени в целом. Например, если говорят о пространстве размерности 3+1, имеется в виду именно пространство-время (а представление размерности в виде суммы обозначает сигнатуру метрики, как раз и определяющую количество пространственных и временных координат этого пространства; во многих теориях количество пространственных координат отличается от трех; существуют и теории с несколькими временными координатами, но последние очень редки).
- ↑ Возможность выбора разных систем пространственно-временных координат и перехода от одной такой системы координат к другой, аналогичен возможности выбора разных (с разным направлением осей) систем декартовых координат в обычном трехмерном пространстве, причем от одной такой системы координат можно перейти к другой поворотом осей и соответcтвующим преобразованием самих координат - чисел, характеризующих положение точки в пространстве относительно данных конкретных декартовых осей. Однако следует заметить, что преобразования Лоренца, служащие аналогом поворотов для пространства-времени, не допускают непрерывного поворота оси времени до произвольного направления, например, ось времени нельзя повернуть до противоположного направления и даже до перпендикулярного (последнему соответствовало бы движение системы отсчета со скоростью света).
Для улучшения этой статьи по физике желательно?:
|
- Пространство в физике
Wikimedia Foundation. 2010.
dic.academic.ru
Пространство и время в философии
Пространство и время в философии – это сложные понятия, с которыми до сих пор связано очень много вопросов. Их изучали не только философы, но и представители других наук: математики, физики и так далее. Такие термины, как «пространство» и «время» в философии появились давно. Первые работы, которые так или иначе связаны с ними, принадлежат Демокриту, Ньютону, Эпикуру.
Пространство и время в философии
Материальный мир, который нас окружает, состоит из различного рода структурных объектов. Эти объекты постоянно находятся в движении, а также развиваются. Развитие же их представляет собой своеобразный процесс развертывания. Проходит этот процесс по определенным этапам.
По сути дела пространство – это не что иное, как способность объекта быть протяжным, иметь место среди других, а также граничить с ними. О времени говорят при сравнении разных длительностей, которые выражают скорость развития процессов развертывания, их темп, а также ритм. Пространство и время в философии всегда имеют определенную связь. Их категории являются формами бытия материи.
Существуют различные концепции, которые имеют пространство и время. Философия их знает две:
- субстанциональная;
- реляционная.
Первая рассматривает и то, и другое как свободные сущности, существующие совершенно независимо от материальных объектов – то есть самостоятельно. Во втором случае они рассматриваются как свободные отношения между объектами, а также процессами. Вне этих объектов и процессов ни того, ни другого не существует.
Как уже говорилось выше, данные понятия рассматриваются и другими науками, однако их основные свойства помогла открыть именно философия. Пространство и время имеют следующие всеобщие свойства:
- независимость от сознания человека;
- неразрывная связь с материей, а также друг с другом;
- абсолютность;
- зависимость от процессов, а также от взаимодействий внутри материальных систем;
- единство непрерывного, а также прерывного в их собственной структуре;
- качественная и количественная бесконечность.
Различают метрические, а также топологические свойства времени и пространства. Топологические характеристики связаны с прерывностью и непрерывностью, ориентируемостью, связанностью, размерностью и так далее. Метрические характеристики отображают изотропность, бесконечность, конечность и прочее.
Всеобщие свойства пространства – это расположенность, протяженность, сосуществование разных элементов, возможность соединения элементов, увеличения или уменьшения их числа.
Метрические свойства в первую очередь связаны именно с протяженностью пространства. Они выражают то, как связаны пространственные элементы, каким законам их связи подчиняются.
Известны также специфические свойства пространства. К ним относят:
- симметрию и асимметрию;
- местоположение;
- расстояние между объектами;
- распределение поля и вещества;
- границы, которые определяют различного рода системы.
Всеобщие свойства времени – это:
- связь с атрибутами материи;
- длительность;
- ассиметричность и одномерность;
- направленность от прошлого к будущему;
- необратимость.
К специфическим свойствам времени можно отнести определенные периоды существования тел, одновременность различных событий, ритм процессов, темпы развития, а также взаимоотношения разных циклов развития, находящихся в одной системе.
Альберт Эйнштейн сумел доказать то, что в нашем мире временные и пространственные интервалы при переходе к другой системе отсчета всегда меняются. Теория относительности сделала наглядной ту глубокую связь, которая существует между пространством и временем. Также она показало, что существуют единое пространство, а также время. То пространство и время, которые мы ощущаем – это всего лишь проекции того самого единого времени и пространства. Они могут расщепляться в зависимости от того, как ведут себя тела.
fb.ru
Определение вероятностного пространства
Теорема о продолжении меры.
Построим минимальную s - алгебру, которой принадлежит поле событий F (например, борелевская s - алгебра - это минимальная s - алгебра, которая содержит поле всех полуинтервалов ненулевой длины).
Тогда доказывается, что счетно-аддитивная функция P(A) однозначно распространяется на все элементы минимальной s - алгебры и при этом ни одна из аксиом не нарушается.
Таким образом, продленное P(A) называется s - аддитивной мерой.
s - алгебра содержит ненаблюдаемые события наряду с наблюдаемыми.
Но в аксиоматической теории вероятности считается, что может произойти любое событие из s - алгебры.
Расширение поля наблюдаемых событий на s - алгебру связано с невозможностью получить основные результаты теории вероятности без понятия s - алгебры.
Вероятностным пространством называется тройка (W, s, P), где
W - пространство элементарных событий, построенное для данного испытания;
s - s-алгебра, заданная на W - системе возможных событий, которая интересует исследователя, в результате проводимых испытаний;
P - s - аддитивная мера, т.е. s - аддитивная неотрицательная функция, аргументами которой являются аргументы из s - алгебры и удовлетворяющая трем аксиомам теории вероятности.
1. 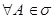
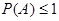 . P(A) - называется вероятностью наступления события A.
. P(A) - называется вероятностью наступления события A.
2. Вероятность достоверного события равна 1 P(W)=1.
3. Вероятность суммы несовместных событий равна сумме вероятностей
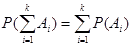
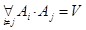 ,
, 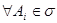 .
.
k - возможно бесконечное число.
Следствие:
Вероятность невозможного события равна 0.
По определению суммы имеет место неравенство W+V=W. W и V несовместные события.
По третей аксиоме теории вероятности имеем:
P(W+V)=P(Q)=P(U)=1
P(W)+P(V)=P(W)
1+P(V)=1
P(V)=1
Пусть W состоит из конечного числа элементарных событий W={E1, E2,..., Em} тогда по определению 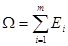 . Элементарные события несовместны, тогда по третей аксиоме теории вероятности имеет место
. Элементарные события несовместны, тогда по третей аксиоме теории вероятности имеет место 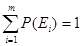
Пусть некоторое событие AÌW состоит из k элементарных событий, тогда {Ei1, Ei2,..., Eik} 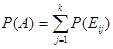
Доказать: Если AÌB, то P(B)³P(A), B=A+C, A и C несовместны.
* Пусть B=A+C, A и B несовместны. Тогда по третей аксиоме теории вероятности P(B)=P(A+C)=P(A)+P(C) т.к. 1³P(C)³0 - положительное число, то P(B)³P(A).
studopedia.ru
 Болезнь определение
Болезнь определение Генетические механизмы определения пола
Генетические механизмы определения пола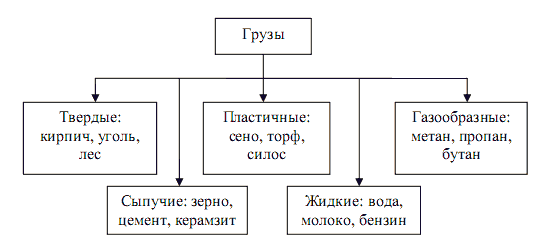 Груз определение
Груз определение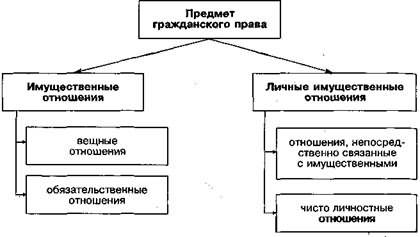 Гражданское право определение
Гражданское право определение Дайте определение понятию авария
Дайте определение понятию авария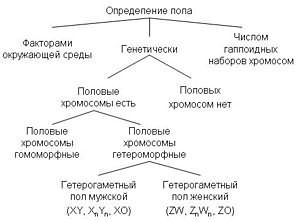 Генетическое определение пола кратко
Генетическое определение пола кратко Акт определение
Акт определение Деятельность определение
Деятельность определение Деталь определение
Деталь определение Жилой дом определение
Жилой дом определение Земля определение
Земля определение