Вероятность событий
Классификация событий
Определение. Случайным событием называется любой факт, который в результате испытания может произойти или не произойти.
Например: 1) появление герба при бросании монеты,
2) выигрыш автомобиля по билету лотереи,
3) выход бракованного изделия с конвейера завода.
Обозначают события заглавными буквами латинского алфавита: A, B, C, ….
Определение.Событие называется достоверным, если в результате испытания оно обязательно должно произойти.
Например, извлечение белого шара из ящика, в котором все шары белые.
Определение.Событие называется невозможным, если в результате оно вообще не может произойти.
Например, извлечение черного шара из ящика, в котором все шары белые.
Определение.Два случайных события 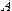 и
и 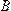 называются несовместными, если появление одного из них исключает появление другого в данном испытании.
называются несовместными, если появление одного из них исключает появление другого в данном испытании.
Например, выпадение орла и выпадение решки при однократном бросании монеты.
Определение.События 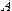 и
и 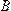 называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Например, получение студентом на зкзамене по одной дисциплине оценок отлично, хорошо, удовлетворительно – события несовместные, а получение тех же оценок на экзамене по трём дисциплинам – события совместные.
Определение.События называются равновозможными, если в результате испытания ни одно из этих событий не является объективно более возможным.
Например, извлечение туза или короля из колоды карт; появление герба или решки при бросании монеты.
Определение.Несколько событий образуют полную группу, если они попарно несовместны и в результате испытания появится только одно из этих событий.
Частным случаем событий, образующих полную группу, являются противоположные события.
Определение.Два несовместных события, из которых в результате испытания одно должно обязательно произойти, называются противоположными.
Обозначают противоположные события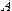 и
и  .
.
Например, при выстреле из ружья попадание – событие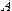 и промах - событие
и промах - событие  ; при бросании монеты выпадение орла – событие
; при бросании монеты выпадение орла – событие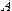 и выпадение решки – событие
и выпадение решки – событие  .
.
Для количественной оценки возможности появления случайного события вводится понятие вероятности. Существует два подхода к определению вероятности в зависимости от возможности проведения опыта. Если оценка осуществляется без опыта, то вероятность называется классической и обозначается  . Если есть возможность провести опыт, то вероятность называется статистической и обозначается
. Если есть возможность провести опыт, то вероятность называется статистической и обозначается 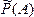 .
.
Определение.Вероятность события 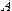 равна отношению числа случаев благоприятствующих ему к общему числу всех равновозможных несовместных элементарных случаев, образующих полную группу
равна отношению числа случаев благоприятствующих ему к общему числу всех равновозможных несовместных элементарных случаев, образующих полную группу
 ,
,
где 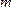 - число случаев благоприятствующих событию
- число случаев благоприятствующих событию 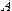 ;
;  – общее число всех возможных элементарных случаев.
– общее число всех возможных элементарных случаев.
Пример 1.1. Бросается игральная кость. Какова вероятность появления чётного числа очков?
Решение. Обозначим через событие 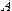 = {появление чётного числа очков}. Общее число исходов
= {появление чётного числа очков}. Общее число исходов 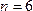
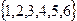 . Число случаев благоприятствующих событию
. Число случаев благоприятствующих событию 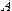
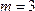
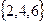 . Тогда вероятность появления четного числа очков равна
. Тогда вероятность появления четного числа очков равна  .
.
studopedia.ru
Теория вероятностей
конспект лекций
Золотарёв Анатолий Петрович
Опыт, явление, событие, предмет теории вероятностей.
Определение.Опытом (испытанием, экспериментом, наблюдением) называется реальная или мысленная реализация определённого комплекса условий (действий). Всё что можно рассматривать в качестве результатов опыта называется событиями опыта или явлениями (если они несут в себе некоторую глобальность). Это различные факты, характеристики, признаки и тп.
События можно разделить на 2 класса: детерминированные и случайные.
Детерминированные события – это такие события, что они при осуществлении опыта всегда наступают или никогда не наступают.
Определение.Событие опыта называется случайным, если при осуществлении опыта оно может произойти. А может не произойти. И предсказать заранее, наступит оно или нет – невозможно.
Простейшие примеры: бросание монетки (выпадёт орёл или решка?), бросание игральных костей, изготовление изделий (на производстве).
В виду постулата о всеобщей связи между предметами и явлениями природы (мироздания) конкретно в опыте мы можем рассмотреть (проанализировать, проконтролировать, искусственно создать) или учесть лишь некоторое число условий (действий). Исключим из рассмотрения многие либо не существенные на наш взгляд, либо не известные на данный момент условия и действия. Случайное с нашей точки зрения событие является как раз закономерным итогом осуществления всего комплекса условий и действия (учтённых и не учтённых).
Эксперимент(испытание, опыт) и случайные события этого опыта называются массовыми, если он может воспроизводиться реально или мысленно неограниченное число раз.
Случайным (стохастическим) экспериментомназывается массовый эксперимент, в котором имеются случайные события и в основном рассматриваются и изучаются случайные события.
Случайным (стохастическим) экспериментомназывается массовый эксперимент, со всем комплексом учтённых и не учтённых условий и действий.
Теория вероятностей возникла из убеждения, что в массовых случайных событиях могут проявляться детерминированные закономерности. Например, массовые случайные события обладают так называемой статистической устойчивостью, суть которой будет рассмотрена ниже. Например, определить однозначно результат выпадения герба или цифры при одном подбрасывании монеты нельзя, но при многократном подбрасывании (порядка тысяч) было обнаружено, что выпадает примерно одинаковое число гербов и цифр, т.е. проявляется такая закономерность.
На данный момент можно определить, предметом теории вероятностейявляется установление и изучение закономерностей в массовых случайных событиях на основе математических моделей стохастических экспериментов.
Предмет теории вероятностей является построением математических моделей для стохастических явлений и изучения в них закономерностей.
Относительная частота события, статистическое определение вероятности событий.
Примем соглашение: место того, чтобы говорить, произведено nповторений одного и того же опыта, будем говорить, что произведеноnопытов.
Событие опыта мы будем обозначать какими либо латинскими буквами или буквами с индексом.
Пусть произведено nопытов, в каждом из которых может появиться или не появиться событиеA. И пусть событие наступилоm раз, тогда событие![]() (1), называется относительной частотой наступления событияAв данной серии изnопытов.
(1), называется относительной частотой наступления событияAв данной серии изnопытов.
Давно было замечено, что во многих опытах, частота имеет тенденцию стабилизироваться около некоторого числа. Это свидетельствует о том, что данное событие обладает определённой степенью объективной возможности появления опыта, меру которой можно представить в виде относительной частоты.
Это эмпирическое свойство случайных событий носит название устойчивости частот и позволяет ввести понятие статистической вероятности событий.
Статистической вероятностьюслучайного события называется число, около которого стабилизируется относительная частота появлений этого события при неограниченном увеличении числа повторений опыта.
Вероятность событияобозначают записью![]() . Следовательно, относительного рассмотренного определения, вероятность приближённо равняется частоте.
. Следовательно, относительного рассмотренного определения, вероятность приближённо равняется частоте.![]() (2)
(2)
Под стабилизацией частотыоколо некоторого числа понимается следующее: начиная с некоторого числа![]() , для любых пар натуральных чисел
, для любых пар натуральных чисел![]() (
(![]() ,
,![]() ),
),![]()
![]() , относительные частоты появлений событияAв
, относительные частоты появлений событияAв![]() сериях опытов мало отличаются друг от друга, и следовательно, любое из них может быть принято за значение вероятности события. В виду такой неоднозначности определения вероятности события согласно формуле в виду практической сложности установлений стабилизации относительной частоты, статистическое определение вероятности события становится неудобным при построении математической модели вероятности этих событий.
сериях опытов мало отличаются друг от друга, и следовательно, любое из них может быть принято за значение вероятности события. В виду такой неоднозначности определения вероятности события согласно формуле в виду практической сложности установлений стабилизации относительной частоты, статистическое определение вероятности события становится неудобным при построении математической модели вероятности этих событий.
StudFiles.ru
1. Случайное событие. Вероятность случайного события. Классическое и статистическое определение вероятности. Понятие о совместных и несовместных событиях. Закон (теорема) сложения вероятностей.
Случайное событие – это любой факт, который в результате испытания может произойти или не произойти. Случайное событие – это результат испытания. Испытание – это эксперимент, выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат.
События обозначаются заглавными буквами латинского алфавита А,В,С.
Численная мера степени объективности возможности наступления события называется вероятностью случайного события.
Классическое определение вероятности события А:
Р(А)=m/n
Вероятность события А равна отношению числа случаев, благоприятствующих событию A(m), к общему числу случаев (n).
Статистическое определение вероятности
Относительная частота событий – это доля тех фактически проведенных испытаний, в которых событие А появилось W=P*(A)= m/n. Это опытная экспериментальная характеристика, где m – число опытов, в которых появилось событие А; n – число всех проведенных опытов.
Вероятностью события называется число, около которого группируются значения частоты данного события в различных сериях большого числа испытаний P(A)=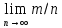 .
.
События называются несовместными, если наступление одного из них исключает появление другого. В противном случае события – совместные.
Сумма двух событий – это такое событие, при котором появляется хотя бы одно из этих событий (А или В).
Если А и В совместные события, то их сумма А+В обозначает наступление события А или события В, или обоих событий вместе.
Если А и В несовместные события, то сумма А+В означает наступление или события А или события В.
2. Понятие о зависимых и независимых событиях. Условная вероятность, закон (теорема) умножения вероятностей. Формула Байеса.
Событие В называется независимым от события А, если появление события А не изменяет вероятности появления события В. Вероятностью появления нескольких независимых событий равна произведению вероятностей этих:
P(AB) = P(A)*P(B)
Для зависимых событий:
P(AB) = P(A)*Р(B/A).
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.
Условная вероятность события В - это вероятность события В, найденная при условии, что событие А произошло. Обозначается Р(В/А)
Произведение двух событий – это событие, состоящее в совместном появлении этих событий (А и В)
Формула Байеса служит для переоценки случайных событий
P(H/A) = (P(H)*P(A/H))/P(A)
P(H) – априорная вероятность события Н
P(H/A) – апостериорная вероятность гипотезы H при условии, что событие А уже произошло
P(A/H) – экспертная оценка
P(A) – полня вероятность события А
3. Распределение дискретных и непрерывных случайных величин и их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение. Нормальный закон распределения непрерывных случайных величин.
Случайная величина – это величина, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений.
Дискретная случайная величина – это случайная величина, когда принимает отдельное изолированное, счетное множество значений.
Непрерывная случайная величина – это случайная величина, принимающая любые значения из некоторого интервала. Понятие непрерывной случайной величины возникает при измерениях.
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.
Таблица – это простейшая форма задания закона распределения
|
Хi |
X1 |
X2 |
… |
Xn |
|
Pi |
P1 |
P2 |
… |
Pn |
Требования:
![]() для дискретных случайных величин
для дискретных случайных величин
Аналитический:
1)F(x)=P(X
Функция распределения = интегральная функция распределения. Для дискретный и непрерывных случайных величин.
2)f(x) = F’(x)
Плотность распределения вероятностей = дифференциальная функция распределения только для непрерывной случайной велечины.
Графический:
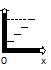 С-ва: 1) 0≤F(x)≤1
С-ва: 1) 0≤F(x)≤1
2) неубывающая для дискретных случайных величин
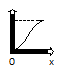 для непрерывных случайных величин
для непрерывных случайных величин
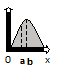 С-ва: 1) f(x)≥0 P(x)=
С-ва: 1) f(x)≥0 P(x)=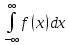
2) площадь S=1
для непрерывных случайных величин
Характеристики:
1.математическое ожидание – среднее наиболее вероятное событие
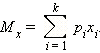
Для дискретных случайных величин.

Для непрерывных случайных величин.
2)Дисперсия – рассеяние вокруг математического ожидания
Для дискретных случайных величин:
![]()
![]()
D(x)=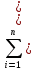 xi-M(x))2*pi
xi-M(x))2*pi
Для непрерывных случайных величин:
D(x)=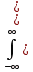 x-M(x))2*f(x)dx
x-M(x))2*f(x)dx
3)Среднее квадратическое отклонение:
σ(х)=√(D(x))
σ – стандартное отклонение или стандарт
х – арифметическое значение корня квадратного из ее дисперсии
Нормальный закон распределения (НЗР) – закон Гаусса
НЗР – это распад вероятностей непрерывной случайной величины, который описывается дифференциальной функцией
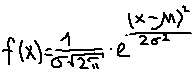
StudFiles.ru
Классическое определение вероятности случайного события
Под вероятностью случайного события в математике понимают меру возможности осуществления данного события в конкретных условиях эксперимента (испытания).
Рассмотрим некоторую конечную полную группу равновоз-можных элементарных событий (исходов) В,, В2, ..., Вп, т. е. совокупность всех единственно возможных, несовместных и вместе с тем равновозможных результатов некоторого испытания, причем пусть интересующее нас случайное событие А осуществляется тогда и только тогда, когда наступают некоторые из элементарных событий указанной полной группы. Пусть таких событий, благоприятствующих для события А, насчитывается т (естественно, тТогда вероятность события А определяют следующим образом:
Определение. Вероятностью Р(А) случайного события А называется отношение количества т элементарных событий, благо-приятствующих событию А, к общему количеству элементарных событий п:
P*(A)=m/n
Поскольку в общем случае 0 < т < п, то из этого определения, называемого классическим определением вероятности случайного события, следует, что вероятность произвольного случайного события принадлежит отрезку [0,1], т.е.
0≤ Р(А)≤1
Пример 8.1. Найти вероятность того, что при извлечении наугад одного шара из корзины, в которой находятся 2 белых, 3 зеленых и 5 красных шаров, извлеченный шар окажется зеленым.
Решение. Поскольку общее количество элементарных событий (исходов) для данного испытания образует полную группу из n=10 равновозможных событий (по общему количеству шаров в корзине), из которых только т = 3 элементарных события (по количеству зеленых шаров) являются благоприятствующими для интересующего нас события (обозначим это событие через А), по формуле (8.1) получим:
Р(А)=3/10
Основные свойства вероятности случайного события
1. Вероятность невозможного события равна нулю. Действительно, поскольку количество т элементарных событий, благоприятствующих невозможному событию А, равно нулю, получаем:
Р(А) = 0/п=0
2. Вероятность достоверного события равна единице. Действительно, поскольку количество т элементарных событий, благоприятствующих достоверному событию А, равно общему количеству п этих элементарных событий, получаем:
Р(А) = п/ п=1
Лекция 1.
Цели, задачи и структура медицинской и биологической физики. Ее место и роль в системе медицинского образования, межпредметные связи с другими медико-биологическими и клиническими дисциплинами.
Вероятностный характер медико-биологических процессов. Элементы теории вероятностей. Вероятность случайного события. Закон сложения и умножения вероятностей.
Принципы вероятностных подходов к задачам диагностики и прогнозирования заболеваний.
Теория вероятностей
В теории вероятностей исследуются закономерности, относящиеся к случайным событиям, величинам, процессам. Врачи редко задумываются, что постановка диагноза имеет вероятностный характер и, как остроумно замечено, лишь патологоанатомическое исследование может достоверно определить диагноз умершего человека.
§2.1. Случайное событие. Вероятность
Наблюдая различные явления, можно заметить, что существует два типа связей между условиями S и наступлением или ненаступлением некоторого событияА. В одних случаях осуществление комплекса условийS(испытание) непременно вызывает событиеА. Так, например, материальная точка массойт0под воздействием силы F(условие S) приобретает ускорение а = F/m0(событие А). В других случаях многократное повторение испытания можетпривести или не привести к появлению события А. Такие события принято называть случайными: к ним можно отнести появление в кабинете врача больного с данной болезнью, выпадение определенной стороны монеты при ее бросании и др.
Не следует думать о случайных явлениях как о беспричинных, ничем не обусловленных. Известно, что многие явления связаны между собой, отдельное явление представляет следствие какого-то другого и само служит причиной последующего. Однако проследить количественно эту связь между условиями и событием часто затруднительно или даже невозможно. Так, при бросании игральной кости (однородный кубик с пронумерованнымишестью гранями: 1, 2, 3, 4, 5 и 6) окончательное положение кубика зависит от движения руки в момент бросания, сопротивления воздуха, положения кубика при попадании на поверхность, особенности поверхности, на которую упал кубик, и других факторов, которые в отдельности учесть невозможно.
В быту применительно к таким случайным событиям употребляют слова «возможно», «вероятно», «маловероятно», «невероятно». В некоторых случаях такая оценка больше характеризует желание говорящего, чем истинную степень возможности или невозможности события. Однако и случайные события, если их число достаточно велико, подчиняются определенным закономерностям. Количественная оценка закономерностей, относящихся к случайным событиям, дается в разделе математики, называемом теорией вероятностей.
Теория вероятностей изучает закономерности, присущие массовым (статистическим) случайным событиям.
Отдельные исторические факты, «неожиданности», «катастрофы» являются единичными, как бы неповторимыми, событиями, и количественные вероятностные суждения относительно них сделать невозможно. Исторически теория вероятностей появилась в связи с попытками подсчета возможности различных исходов в азартных играх. В настоящее же время она применяется в науке, в том числе биологии и медицине, для оценки вероятности практически важных событий. От игр остались лишь наглядные примеры, которые удобно использовать для иллюстрации теоретических положений.
Статистическое определение вероятности. ВероятностьР(А) в теории вероятностей выступает как числовая характеристика степени возможности появления какого-либо определенного случайного события А при многократном повторении испытаний.
Допустим, при 1000 бросаний игральной кости цифра 4 выпадает 160 раз. Отношение 160/1000 = 0,16 показывает относительную частоту выпадания цифры 4 в данной серии испытаний. В более общем случае, когда случайное событие А происходитт раз в сериип независимых испытаний,относительной частотой события в данной серии испытаний или просто частотой события А называют отношение
![]() (2.1)
(2.1)
При большом числе испытаний частота события примерно постоянна: увеличение числа испытаний уменьшает колебание частоты события около постоянной величины.
Вероятностью случайного события назовем предел, к которому стремится частота события при неограниченном увеличении числа испытаний:
![]() (2.2)
(2.2)
Естественно, что никто и никогда не сможет проделать неограниченное число испытаний для того, чтобы определить вероятность. В этом нет и надобности. Практически за вероятность [см. (2.2)] можно принять относительную частоту события при большом числе испытаний. Так, например, из статистических закономерностей рождения, установленных за много лет наблюдений, вероятность того события, что новорожденный будет мальчиком, оценивают в 0,515.
Классическое определение вероятности.Если при испытаниях нет каких-либо причин, вследствие которых одно случайноесобытие появлялось бы чаще других (равновозможные события), можно определить вероятность исходя из теоретических соображений. Например, выясним в случае бросания монеты частоту выпадания герба (событиеА). Разными экспериментаторамипри нескольких тысячах испытаний было показано, что относительная частота такого события принимает значения, близкие к0,5. Учитывая, что появление герба и противоположной стороны монеты (событие В) являются событиями равновозможными, если монета симметрична, суждение Р(А) = Р(В) = 0,5 можно было бы сделать и без определения частоты этих событий. На основе понятия «равновозможности» событий формулируется другое определение вероятности.
Допустим, что в результате испытания должно произойти только одно изп равновозможных несовместных событий(несовместными называют события, если их одновременное осуществление невозможно). Пусть рассматриваемое событие А происходит вт случаях, которые называются благоприятствующими А, ине происходит при остальных п - т, неблагоприятствующих А. Тогдавероятностью можно назвать отношение благоприятствующих случаев к общему числу равновозможных несовместных событий:
Р(А) = m/n.(2.3)
Это классическое определение вероятности.
Рассмотрим несколько примеров.
1. В урне находится 40 шаров: 10 черных и 30 белых. Найти вероятность того, что вынутый наугад один шар будет черным.
Число благоприятствующих случаев равно числу черных шаров в урне: т = 10. Общее число равновозможных событий (вынимание одного шара) равно полному числу шаров в урне: п = 40. Эти события несовместны, так как вынимается один и только один шар. По формуле (2.3) имеем:
Р(А) = 10/40 = 1/4.
2. Найти вероятность выпадания четного числа при бросании игральной кости.
При бросании кости реализуются шесть равновозможных несовместных событий: появление одной цифры 1, 2, 3, 4, 5 или 6, т. е. п = 6.Благоприятствующими случаями являются выпадания одной из цифр 2, 4 или 6: т = 3. Искомая вероятность:
Р(А) = m/n– 3/6 = 1/2.
Как видно из определений вероятности события (2.2) и (2.3), для всех событий 0 Р(А) 1.
События, которые при данных испытаниях не могут произойти, называются невозможными: их вероятность равна нулю.
Так, например, невозможно из урны с белыми и черными шарами вытащить красный шар, невозможно на игральной кости получить цифру 7.
Событие, которое при данном испытании обязательно произойдет, называется достоверным, его вероятность равна 1.
Примером достоверного события является извлечение белого шара из урны, в которой находятся только белые шары.
В ряде случаев вычислить вероятность события оказывается проще, если представить его в виде комбинации более простых событий. Этой цели служат некоторые теоремы теории вероятностей.
Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме их вероятностей. Для двух несовместных событий
Р(А илиВ) = Р(А) + Р(В).(2.4)
Докажем эту теорему. Пусть п — общее число испытаний, т1— число случаев, благоприятствующих событию А,т2— число случаев, благоприятствующих событию В. Число случаев, благоприятствующих наступлению либо события А, либо события В, равно m1 +m2. ТогдаР(А илиВ) = (т1+ т2)/п = т1/п + т2/п. Отсюда, учитывая (2.3), имеем
Р(А илиВ) = Р(А) + Р(В).
* Найти вероятность выпадания 1 или 6 при бросании игральной кости.
События А (выпадание 1) иВ (выпадание 6) являются равновозможными: Р(А) = Р(В) = 1/6, поэтому из (2.4) находимР(А илиВ) =1/6 + 1/6 = 1/3.
Сложение вероятностей справедливо не только для двух, но и для любого числа несовместных событий.
* В урне находится 50 шаров: 10 белых, 20 черных, 5 красных и 15 синих. Найти вероятность появления белого, или черного, или красного шара при однократной операции изъятия шара из урны.
Вероятность вынимания белого шара (событие А) равна Р(А) = 10/50 = 1/5, черного шара (событие В) — Р(В) = 20/50 = 2/5 и красного (событие С) — Р(С) = 5/50 = 1/10. Отсюда по формуле сложения вероятностей получим Р(А или В или С) = Р(А) + Р(В) + Р(С) = 1/5 + 2/5 + + 1/10= 7/10.
Если два события единственно возможны и несовместны, то их называют противоположными.
Такие события принято обозначать, например, А и![]() .
.
Сумма вероятностей двух противоположных событий, как следует из теоремы сложения вероятностей, равна единице:
![]() (2.5)
(2.5)
*Проиллюстрируем справедливость (2.5) на предыдущем примере. Пусть вынимание белого, или черного, или красного шара будет событиемА1 , Р(А1) = 7/10.Противоположным событием![]() является доставание синего шара. Так как синих шаров 15, а общее количество шаров 50, то получаемР(
является доставание синего шара. Так как синих шаров 15, а общее количество шаров 50, то получаемР(![]() ) = 15/50 = 3/10 иР(А1) + Р(
) = 15/50 = 3/10 иР(А1) + Р(![]() ) = 7/10 + 3/10 = = 1.
) = 7/10 + 3/10 = = 1.
*В урне находятся белые, черные и красные шары. Вероятность доставания черного или красного шара равна 0,4. Найти вероятность доставания из урны белого шара.
Обозначим А событие вынимания черного или красного шара, Р(А) = 0,4; противоположным событием ![]() будет изъятие белого шара, тогда на основании (2.5) вероятность этого события Р(
будет изъятие белого шара, тогда на основании (2.5) вероятность этого события Р(![]() ) = 1 - Р(А) = = 1 - 0,4 = 0,6.
) = 1 - Р(А) = = 1 - 0,4 = 0,6.
Систему событий (А1, А2, ... Ak) называют полной, если при испытаниях наступит одно и только одно из этих событий. Сумма вероятностей событий, образующих полную систему, равна единице.
* В урне имеется 40 шаров: 20 белых, 15 черных и 5 красных. Вероятность появления белого шара (событие А) равна Р(А) = 20/40 = 1/2, для черного шара (событие В) — Р(В) = 15/40 = 3/8 и для красного шара (событиеС) — Р(С) = 5/40 = 1/8. В этом случае система событийА1, А2, А3 является полной; можно убедиться, что Р(А) + Р(В) + Р(С) = 1/2 + 3/8 + + 1/8 = 1.
Теорема умножения вероятностей: вероятность совместного появления независимых событий равна произведению их вероятностей. Для двух событий
Р(А и В) = Р(А) • Р(В). (2.6)
Докажем эту теорему. Так как события А и В независимы, то каждому из т1 случаев, благоприятствующих А, соответствуют т2случаев, благоприятствующих В. Таким образом, общее число случаев, благоприятствующих совместному появлению событий А и В, равно т1т2. Аналогично, общее число равновозможных событий равно п1 п2, где п1 и п2— числа равновозможных событий соответственно для А и В. Имеем
![]() (2.7)
(2.7)
* В одной урне находится 5 черных и 10 белых шаров, в другой 3 черных и 17 белых. Найти вероятность того, что при первом вынимании шаров из каждой урны оба шара окажутся:
1) черными; 2) белыми; 3) в первой урне будет вынут черный шар, а во второй — белый; 4) в первой урне будет вынут белый шар, а во второй — черный.
Вероятность вытаскивания черного шара из первой урны (событие А)равна Р(А) =
= 5/15 = 1/3, черного шара из второй урны (событие В) — Р(В) = 3/20, белого шара из первой урны (событие А') — Р(А') = 10/15 = 2/3 и белого шара из первой урны (событиеВ') —Р(В') = 17/20. Находим вероятность совместного появления двух независимых событий по формуле (2.6):
1)Р(А и В) = Р(А) • Р(В) = (1/3) (3/20) = 3/60 — оба шара черные;
2) Р(А' и В') = Р(А') • Р(В') = (2/3) (17/20) = 17/30 — оба шара белые;
3) Р(А' и В') = Р(А) • Р(В') = (1/3) (17/20)= 17/60 — в первой урне будет вынут черный шар, а во второй — белый;
4) Р(А' и В) = Р(А') • Р(В) = (2/3) (3/20) = 1/10 — в первой урне будет вынут белый шар, а во второй — черный.
Все четыре возможных случая А и В, А' и В', А и В', А' и В образуют полную систему событий, поэтому
Р(А иВ) + Р(А' и В') + Р(А и В') + Р(А' иВ)= 3/60 + 17/30 + 17/60 + 1/10 = 1.
* Найти вероятность того, что в семье с тремя детьми все трое сыновья. Считать, что вероятность рождения мальчика равна 0,515 и по каждого последующего ребенка не зависит от пола предыдущих детей.
По теореме умножения вероятностей, Р(А и В иС) = 0,515• 0,515 • 0,515 0,14.
Теорема умножения вероятностей усложняется, если определяется вероятность события, состоящего из совместного появления двух зависимых между собой событий. В том случае, когда событие В выполняется при условии, что событие А имело место, вероятность совместного появления двух этих событий равна
Р(А и В) = Р(А) • Р(В/А),(2.8)
где Р(В/А) —условная вероятность, т. е. вероятность событияВ при условии, что событиеА состоялось.
* В урне 5 шаров: 3 белых и 2 черных. Найти вероятность того, что последовательно один за другим будут вынуты черный и белый шары.
Вероятность того, что первым будет изъят черный шар (событие А),равна Р(А) = т/п = 2/5. После удаления черного шара в урне остается 4 шара: 3 белых и 1 черный. В этом случае вероятность вынимания белогошара (событие В после выполнения события А) равна Р(В/А) = 3/4. Используя (2.8), получаем
Р(А и В) = (2/5) • (3/4) = 3/10.
StudFiles.ru
Независимость (теория вероятностей)
У этого термина существуют и другие значения, см. Независимость (значения).В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
Независимые события
Будем считать, что дано фиксированное вероятностное пространство ( Ω , F , P ) {\displaystyle (\Omega ,\;{\mathcal {F}},\;\mathbb {P} )} .
Определение 1. Два события A , B ∈ F {\displaystyle A,B\in {\mathcal {F}}} независимы, если
Вероятность появления события A {\displaystyle A} не меняет вероятности события B {\displaystyle B} .Замечание 1. В том случае, если вероятность одного события, скажем B {\displaystyle B} , ненулевая, то есть P ( B ) > 0 {\displaystyle \mathbb {P} (B)>0} , определение независимости эквивалентно:
P ( A ∣ B ) = P ( A ) , {\displaystyle \mathbb {P} (A\mid B)=\mathbb {P} (A),}то есть условная вероятность события A {\displaystyle A} при условии B {\displaystyle B} равна безусловной вероятности события A {\displaystyle A} .
Определение 2. Пусть есть семейство (конечное или бесконечное) случайных событий { A i } i ∈ I ⊂ F {\displaystyle \{A_{i}\}_{i\in I}\subset {\mathcal {F}}} , где I {\displaystyle I} — произвольное индексное множество. Тогда эти события попарно независимы, если любые два события из этого семейства независимы, то есть
P ( A i ∩ A j ) = P ( A i ) ⋅ P ( A j ) , ∀ i ≠ j . {\displaystyle \mathbb {P} (A_{i}\cap A_{j})=\mathbb {P} (A_{i})\cdot \mathbb {P} (A_{j}),\;\forall i\neq j.}Определение 3. Пусть есть семейство (конечное или бесконечное) случайных событий { A i } i ∈ I ⊂ F {\displaystyle \{A_{i}\}_{i\in I}\subset {\mathcal {F}}} . Тогда эти события совместно независимы, если для любого конечного набора этих событий { A i k } k = 1 N {\displaystyle \{A_{i_{k}}\}_{k=1}^{N}} верно:
P ( A i 1 ∩ … ∩ A i N ) = P ( A i 1 ) ⋅ … ⋅ P ( A i N ) . {\displaystyle \mathbb {P} (A_{i_{1}}\cap \ldots \cap A_{i_{N}})=\mathbb {P} (A_{i_{1}})\cdot \ldots \cdot \mathbb {P} (A_{i_{N}}).}Замечание 2. Совместная независимость, очевидно, влечет попарную независимость. Обратное, вообще говоря, неверно.
Пример 1. Пусть брошены три уравновешенные монеты. Определим события следующим образом:
- A 1 {\displaystyle A_{1}} : монеты 1 и 2 упали одной и той же стороной;
- A 2 {\displaystyle A_{2}} : монеты 2 и 3 упали одной и той же стороной;
- A 3 {\displaystyle A_{3}} : монеты 1 и 3 упали одной и той же стороной;
Легко проверить, что любые два события из этого набора независимы. Все же три в совокупности зависимы, ибо зная, например, что события A 1 {\displaystyle A_{1}} и A 2 {\displaystyle A_{2}} произошли, мы знаем точно, что A 3 {\displaystyle A_{3}} также произошло. Более формально: P ( A i ∩ A j ) = 1 4 = 1 2 ⋅ 1 2 = P ( A i ) ⋅ P ( A j ) ∀ i ≠ j {\displaystyle \mathbb {P} (A_{i}\cap A_{j})={\frac {1}{4}}={\frac {1}{2}}\cdot {\frac {1}{2}}=\mathbb {P} (A_{i})\cdot \mathbb {P} (A_{j})\quad \forall i\neq j} . С другой стороны, P ( A 1 ∩ A 2 ∩ A 3 ) = 1 4 ≠ 1 2 ⋅ 1 2 ⋅ 1 2 = P ( A 1 ) ⋅ P ( A 2 ) ⋅ P ( A 3 ) {\displaystyle \mathbb {P} (A_{1}\cap A_{2}\cap A_{3})={\frac {1}{4}}\neq {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}=\mathbb {P} (A_{1})\cdot \mathbb {P} (A_{2})\cdot \mathbb {P} (A_{3})} .
Независимые сигма-алгебры
Определение 4. Пусть A 1 , A 2 ⊂ F {\displaystyle {\mathcal {A}}_{1},\;{\mathcal {A}}_{2}\subset {\mathcal {F}}} две сигма-алгебры на одном и том же вероятностном пространстве. Они называются независимыми, если любые их представители независимы между собой, то есть:
P ( A 1 ∩ A 2 ) = P ( A 1 ) ⋅ P ( A 2 ) , ∀ A 1 ∈ A 1 , A 2 ∈ A 2 {\displaystyle \mathbb {P} (A_{1}\cap A_{2})=\mathbb {P} (A_{1})\cdot \mathbb {P} (A_{2}),\;\forall A_{1}\in {\mathcal {A}}_{1},\;A_{2}\in {\mathcal {A}}_{2}} .Если вместо двух имеется целое семейство (возможно бесконечное) сигма-алгебр, то для него определяется попарная и совместная независимость очевидным образом.
Независимые случайные величины
Определения
Определение 5. Пусть дано семейство случайных величин ( X i ) i ∈ I {\displaystyle (X_{i})_{i\in I}} , так что X i : Ω → R , ∀ i ∈ I {\displaystyle X_{i}\colon \Omega \to \mathbb {R} ,\;\forall i\in I} . Тогда эти случайные величины попарно независимы, если попарно независимы порождённые ими сигма-алгебры { σ ( X i ) } i ∈ I {\displaystyle \{\sigma (X_{i})\}_{i\in I}} . Случайные величины независимы в совокупности, если таковы порождённые ими сигма-алгебры.
Определение, данное выше, эквивалентно любому другому из нижеперечисленных. Две случайные величины X , Y {\displaystyle X,\;Y} независимы тогда и только тогда, когда:
- Для любых A , B ∈ B ( R ) {\displaystyle A,\;B\in {\mathcal {B}}(\mathbb {R} )} :
- Для любых борелевских функций f , g : R → R {\displaystyle f,\;g\colon \mathbb {R} \to \mathbb {R} } случайные величины f ( X ) , g ( Y ) {\displaystyle f(X),\;g(Y)} независимы.
- Для любых ограниченных борелевских функций f , g : R → R {\displaystyle f,\;g\colon \mathbb {R} \to \mathbb {R} } :
Свойства независимых случайных величин
- Пусть P X , Y {\displaystyle \mathbb {P} ^{X,\;Y}} — распределение случайного вектора ( X , Y ) {\displaystyle (X,\;Y)} , P X {\displaystyle \mathbb {P} ^{X}} — распределение X {\displaystyle X} и P Y {\displaystyle \mathbb {P} ^{Y}} — распределение Y {\displaystyle Y} . Тогда X , Y {\displaystyle X,\;Y} независимы тогда и только тогда, когда
где ⊗ {\displaystyle \otimes } обозначает (прямое) произведение мер.
- Пусть F X , Y , F X , F Y {\displaystyle F_{X,\;Y},\;F_{X},\;F_{Y}} — кумулятивные функции распределения ( X , Y ) , X , Y {\displaystyle (X,\;Y),\;X,\;Y} соответственно. Тогда X , Y {\displaystyle X,\;Y} независимы тогда и только тогда, когда
- Пусть случайные величины X , Y {\displaystyle X,\;Y} дискретны. Тогда они независимы тогда и только тогда, когда
- Пусть случайные величины X , Y {\displaystyle X,\;Y} совместно абсолютно непрерывны, то есть их совместное распределение имеет плотность f X , Y ( x , y ) {\displaystyle f_{X,\;Y}(x,\;y)} . Тогда они независимы тогда и только тогда, когда
где f X ( x ) , f Y ( y ) {\displaystyle f_{X}(x),\;f_{Y}(y)} — плотности случайных величин X {\displaystyle X} и Y {\displaystyle Y} соответственно.
| В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 14 мая 2011 года. |
ru.wikipedia.org
Читайте также
![Акт определение Акт определение]() Акт определение
Акт определение- Актив определение
![База данных определение База данных определение]() База данных определение
База данных определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Власть определение Власть определение]() Власть определение
Власть определение- Выберите один из вариантов определения истины это
![Гражданская оборона определение Гражданская оборона определение]() Гражданская оборона определение
Гражданская оборона определение![Гражданское право определение Гражданское право определение]() Гражданское право определение
Гражданское право определение![Гражданская война определение Гражданская война определение]() Гражданская война определение
Гражданская война определение![Дайте определение понятию авария Дайте определение понятию авария]() Дайте определение понятию авария
Дайте определение понятию авария![Генетическое определение пола кратко Генетическое определение пола кратко]() Генетическое определение пола кратко
Генетическое определение пола кратко![Генетические механизмы определения пола Генетические механизмы определения пола]() Генетические механизмы определения пола
Генетические механизмы определения пола
 Акт определение
Акт определение База данных определение
База данных определение Болезнь определение
Болезнь определение Власть определение
Власть определение Гражданская оборона определение
Гражданская оборона определение Гражданское право определение
Гражданское право определение Гражданская война определение
Гражданская война определение Дайте определение понятию авария
Дайте определение понятию авария Генетическое определение пола кратко
Генетическое определение пола кратко Генетические механизмы определения пола
Генетические механизмы определения пола