Понятие функции. Способы задания функции
Понятие функции является одним из основных понятий современной математики. С этим понятием часто встречаются при изучении реальных процессов в природе, науке и технике. С помощью различных функций могут быть описаны многие процессы и явления реального мира.
Определение. Отображения 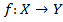 , где
, где 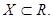 будем называть (вещественной) функцией действительного переменного.
будем называть (вещественной) функцией действительного переменного.  - область определения - совокупность всех значений независимой переменной х, для которых функция определена.
- область определения - совокупность всех значений независимой переменной х, для которых функция определена.
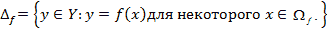 - множество значений f или образ f.
- множество значений f или образ f.
Определение. Если каждому элементу х множества X ( 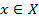 ) ставится в соответствие вполне определенный элемент у множества Y
) ставится в соответствие вполне определенный элемент у множества Y 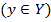 , то говорят, что на множестве X задана функция.
, то говорят, что на множестве X задана функция.
y = f(x), y = F(x) - функциональная зависимость х и у.
f, F - характеристики функции, х - независимая переменная (аргумент),
у - зависимая переменная.
Рассматривают три способа задания функции: аналитический, табличный и графический.
1. Аналитический.
Способ задания функции при помощи формулы называется аналитическим.Этот способ является основным в мат. анализе, но на практике не удобен.
2. Табличный способ задания функции.
Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие им значения функции.
3. Графический способ задания функции.
Функция у = f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями
Классификация функций.
Элементарные функции разделяют на алгебраические и неалгебраические (трансцендентные).
Алгебраической называют функцию, в которой над аргументом производится конечное число алгебраических действий.
К ним относятся:
- целая рациональная функция (многочлен, полином)
- дробно-рациональная функция – отношение двух многочленов
- иррациональная функция (среди действий над аргументом есть извлечение корня).
К трансцендентным относятся: показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.
Четные и нечетные функции.
Функция у = f(х) называется четной или нечетной, если она определена на множестве симметричном относительно нулевой точки и обладает на нем свойством f(-x)=f(x) или свойством f(-x) = -f(x). В противном случае функцией общего вида. График четной функции симметричен относительно оси ординат, график нечетной симметричен относительно начала координат.
Произведения двух четных или двух нечетных функций есть функция четная, произведения четной функции на нечетную есть нечетная функция
Монотонные функции.
Пусть (a,b) промежуток с концами в точках a и b, где a.
Функция у = f(х) называется возрастающей (убывающей) на промежутке (a,b), если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 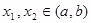 и
и 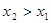 .
.
Тогда функция возрастает на промежутке X, если  (запись
(запись 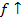 на (a,b)) и убывает, если
на (a,b)) и убывает, если 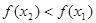 (запись
(запись 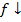 на (a,b)) (см. рис. 1).
на (a,b)) (см. рис. 1).
Запись 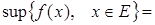
 и
и 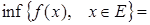
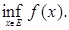
Функции возрастающие и убывающие называется монотонными. К монотонным функциям относятся также неубывающие и невозрастающие функции.
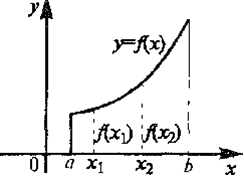
Рис.1
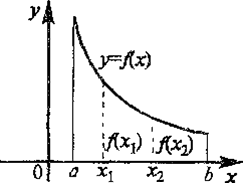
Рис. 2.
Ограниченные функции.
Функция называется ограниченной на промежутке (a,b), если 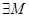 такое, что
такое, что

 .
.
В противном случае функция называется неограниченной.
Периодическая функция.
Функция называется периодической с периодом 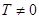 , если
, если 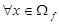 справедливо
справедливо 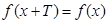 .
.
studopedia.ru
27. Понятие функции. Область определения. Различные способы задания.
Величина у наз. функцией переменной величины х, если каждому из тех значений, которые может принимать х, соответствует одно или несколько определенных значений у. При этом переменная величина х называется аргументом.
Совокупность всех значений, которые может принимать аргумент х функции f(х), называется областью определения этой функции. Замечание: значению х, не входящему в упомянутую совокупность, не соответствует никакое значение функции.
Ф-я считается заданной (известной), если для каждого значения аргумента (из числа множества) можно узнать соответствующее значение ф-и. 3 способа задания ф-и: 1)табличный, 2)графический, 3)аналитический. Табличный способ сразу дает числовое значение ф-и. Графический способ сост. в построении линии (графика), у которого абсциссы изображают значения аргумента, а ординаты – соответствующие значения ф-и. аналитический способ сост. в задании ф-и одной или несколькими формулами.
28.Числовая последовательность. Определение предела числовой последовательности.
Если для каждого элмента из некоторого множества взаимнооднозначно сопоставлено натуральное число (т.е. задан номер), то говорят, что задана последовательность{xn}, xn – общий элемент последовательности. Число А называется пределом числовой последовательности {xn}, если для любого ε>0 существует номер N=N(ε)>0 такой, что для всех номеров n>N выполняется неравенство | xn–A| < ε. ![]() . Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
. Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
29.Определение бесконечно большой и бесконечно малой последовательности. Связь между ними. Операции над бесконечно малыми последовательностями.
Бесконечно малой наз. последовательность, предел которой равен нулю. Бесконечно большой величиной наз. переменная величина, абсолютное значение которой неограниченно возрастает. Связь между ними: если у – бесконечно большая величина, то ![]() - бесконечно малая; если у – бесконечно малая величина, то
- бесконечно малая; если у – бесконечно малая величина, то ![]() - бесконечно большая.
- бесконечно большая.
Сравнение бесконечно малых величин: 1)если отношение ![]() двух бесконечно малых величин само бесконечно мало( т.е. lim
двух бесконечно малых величин само бесконечно мало( т.е. lim![]() =0, а значит
=0, а значит
lim![]() = ∞), то β наз. величиной высшего порядка малости относительно α; при этом α наз. величиной низшего порядка малости относительно β. 2)если отношение
= ∞), то β наз. величиной высшего порядка малости относительно α; при этом α наз. величиной низшего порядка малости относительно β. 2)если отношение ![]() двух бесконечно малых величин стремится к конечному пределу, не равному нулю, то α и β наз. бесконечно малыми одного и того же порядка малости. Эквивалентные бесконечно малые величины всегда имеют один и тот же порядок. 3)бесконечно малая величина β имеет т-й порядок иалости относительно относительно бесконечно малой α, если β имеет тот же порядок малости, что αт, т.е. если отношение
двух бесконечно малых величин стремится к конечному пределу, не равному нулю, то α и β наз. бесконечно малыми одного и того же порядка малости. Эквивалентные бесконечно малые величины всегда имеют один и тот же порядок. 3)бесконечно малая величина β имеет т-й порядок иалости относительно относительно бесконечно малой α, если β имеет тот же порядок малости, что αт, т.е. если отношение ![]() имеет конечный предел, не равный нулю.
имеет конечный предел, не равный нулю.
30.Предел функции в точке. Односторонние пределы.
Число А наз. пределом ф-и у = f(х) в точке Х0 (при Х→ Х0) если для любого положительного числа ε можно найти такое положительное число δ, что для всех Х из проколотой δ-окрестности точки Х0соответствует значение у попадают в ε-окрестность. ![]() f(х) =А. Число В наз. пределом ф-и у = f(х) в точке а справа, если для любого ε>0 найдется δ>0, такое что из условия 0x-a< δ следует |B-f(x)|< ε. В=
f(х) =А. Число В наз. пределом ф-и у = f(х) в точке а справа, если для любого ε>0 найдется δ>0, такое что из условия 0x-a< δ следует |B-f(x)|< ε. В=![]() f(х). Число В наз. пределом ф-и у = f(х) в точке а слева, если для любого ε>0 найдется δ>0, такое что из условия 0x-a< δ следует |B-f(x)|< ε. В=
f(х). Число В наз. пределом ф-и у = f(х) в точке а слева, если для любого ε>0 найдется δ>0, такое что из условия 0x-a< δ следует |B-f(x)|< ε. В=![]() f(х). Ф-я наз. непрерывной в точке а справа (слева), если
f(х). Ф-я наз. непрерывной в точке а справа (слева), если ![]() f(х)= f(а)
f(х)= f(а)
(![]() f(х)= f(а)).
f(х)= f(а)).


StudFiles.ru
Способы задания функции.
Лекция 3. Числовые функции, способы задания и график.
Функция-зависимость переменной у от переменной x,если каждому значению х соответствует единственное значение у.
Переменная х-независимая переменная.
Переменная у- зависимая переменная
Значение функции-значение у, соответствующее заданному значению х.
Область определения функции- все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- все значения, которые принимает функция.
Множество X называется областью определения функции f, а множество Y – областью значений. Обозначают: Df и Ef. Если ясно, какие множества X и Y имеются в виду, то пишут y = f (x) . Элемент x называется аргументом, а y – значением функции f.
Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)
Функция является нечетной-если для любого х из области определения функции выполняется равенство f(-x)=-f(x)
Возрастающая функция-если для любых х1и х2,таких, что х1< х2, выполняется неравенство f(х1)2)
Убывающая функция-если для любых х1и х2,таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
Способы задания функции.
Графиком функции (в декартовой прямоугольной системе координат)
называют геометрическое место точек, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции.
Существует несколько способов задания функции.
Табличный. Используется тогда, когда область определения состоит из
конечного множества чисел. Тогда для задания функции проще всего указать
таблицу, содержащую значения аргумента и соответствующие значения
функции. Например, таблица логарифмов. Другим примером могут быть
таблицы, содержащие данные о числе жителей, населяющих земной шар в
отдельные годы, расписания движения поездов и т.п.
Аналитический. Прианалитическом способе задания функция может
быть задана явно, когда дано выражение у через x, т.е. формула имеет вид
y = f (x) неявно, когда х и у связаны между собой уравнением вида F(x, y) = 0 ;
параметрически, когда соответствующие друг другу значения х и у выражены через третью переменную величину t, называемую параметром.
Логический. Если функция описывается правилом ее составления,
например, функция Дирихле: f(x)= 1, если x – рациональное; f(x)= 0, если x –
иррациональное.
Графический. Состоит в изображении графика функции – множества
точек (x, y) плоскости, абсциссы которых есть значения аргумента x, а
ординаты – соответствующие им значения функции y = f (x) . Преимуществом
графического задания является его наглядность, недостатком – его
неточность.
studopedia.ru
Понятие функции
Пусть Х и Y – некоторые числовые множества и пусть указано правило, по которому каждому элементу х множества Х поставлено в соответствие единственное значение у из множества Y. Это соответствие называется функцией и обозначается 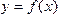 . Переменная х называется независимой или аргументом, переменная у – зависимой или функцией. Множество Х называется областью определения функции и обозначается D(f ). Множество Y (множество всех значений, которые принимает переменная у) называется областью изменения (областью значений) функции и обозначается E(f ).
. Переменная х называется независимой или аргументом, переменная у – зависимой или функцией. Множество Х называется областью определения функции и обозначается D(f ). Множество Y (множество всех значений, которые принимает переменная у) называется областью изменения (областью значений) функции и обозначается E(f ).
Две функции называются равными, если они имеют одинаковые области определения и каждому значению аргумента они ставят в соответствие одно и тоже число.
Наиболее распространенный способ задания функции – аналитический, то есть с помощью формулы. Например, функцию, ставящую в соответствие каждому неотрицательному числу х его квадратный корень, можно записать в виде  или
или 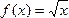 . Этот способ задания функции компактен, содержит полную информацию о свойствах функции и наиболее удобен при проведении расчетов. Если не сделано специальной оговорки, то за область определения функции берут все значения аргумента, для которых указанные в формуле действия выполнимы. Например, область определения функции
. Этот способ задания функции компактен, содержит полную информацию о свойствах функции и наиболее удобен при проведении расчетов. Если не сделано специальной оговорки, то за область определения функции берут все значения аргумента, для которых указанные в формуле действия выполнимы. Например, область определения функции 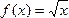 все неотрицательные значения х, то есть
все неотрицательные значения х, то есть 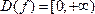 , а для функции
, а для функции 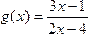 – область определения все действительные значения х, кроме
– область определения все действительные значения х, кроме 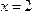 , то есть D(g) = ¡\{2}.
, то есть D(g) = ¡\{2}.
Иногда для разных значений х функция задается разными формулами. В этом случае используют обозначение: 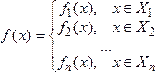 , причем
, причем 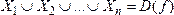 . График такой функции состоит из n частей.
. График такой функции состоит из n частей.
На практике часто используют табличный способ задания функции. При этом способе задания функции приводится таблица, в которой для имеющихся значений аргумента указываются соответствующие значения функции. Табличный способ важен потому, что он является основным при описании реальных зависимостей, возникающих при проведении различных экспериментов. С математической точки зрения табличное задание функции неполно, так как оно позволяет найти значение функции только для тех значений аргумента, которые заданы в таблице. Однако оно позволяет высказать предположение об аналитическом представлении функции, и, применяя различные методы приближенных вычислений, найти это представление.
Рассмотрим декартову систему координат на плоскости. Множество точек плоскости, координаты которых удовлетворяют условию 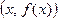 , называется графиком функции y = f (x). Графическое представление функции удобно для непосредственного восприятия ее особенностей, описания свойств. Однако графический способ неудобен при выполнении расчетов.
, называется графиком функции y = f (x). Графическое представление функции удобно для непосредственного восприятия ее особенностей, описания свойств. Однако графический способ неудобен при выполнении расчетов.
 Функции можно также задавать словесно. Например, функция Дирихле задается таким описанием: значение функции равно 1, если x рационально, и 0, если x иррационально.
Функции можно также задавать словесно. Например, функция Дирихле задается таким описанием: значение функции равно 1, если x рационально, и 0, если x иррационально.
Примеры функций:
|
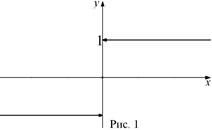
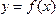 каждому положительному числу х ставит в соответствие число
каждому положительному числу х ставит в соответствие число 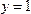 , каждому отрицательному числу х ставит в соответствие число
, каждому отрицательному числу х ставит в соответствие число 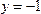 и
и  (рис. 1). Эта функция называется знаком числа х и обозначается
(рис. 1). Эта функция называется знаком числа х и обозначается 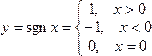 .
.
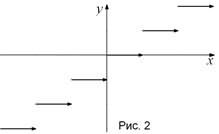 2. Функция
2. Функция 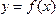 каждому числу
каждому числу  , где n Î ¢, ставит в соответствие число n (рис. 2). Эта функция называется целой частью числа х и обозначается
, где n Î ¢, ставит в соответствие число n (рис. 2). Эта функция называется целой частью числа х и обозначается 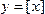 .
.


 3. Функция
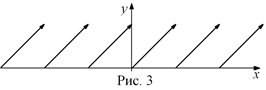
3. Функция 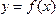 каждому числу
каждому числу  , где n Î ¢, ставит в соответствие число
, где n Î ¢, ставит в соответствие число  (рис. 3). Эта функция называется дробной частью числа х и обозначается
(рис. 3). Эта функция называется дробной частью числа х и обозначается  .
.
studopedia.ru
Читайте также
![Область определения сложной функции Область определения сложной функции]() Область определения сложной функции
Область определения сложной функции- Как найти область определения функции
![Функции нескольких переменных область определения линии уровня Функции нескольких переменных область определения линии уровня]() Функции нескольких переменных область определения линии уровня
Функции нескольких переменных область определения линии уровня![Как обозначается область определения функции Как обозначается область определения функции]() Как обозначается область определения функции
Как обозначается область определения функции- Дать определение понятию индустриализация
![Какое краткое определение соответствует понятию государства Какое краткое определение соответствует понятию государства]() Какое краткое определение соответствует понятию государства
Какое краткое определение соответствует понятию государства- Определение понятия предпринимательской деятельности содержится в
![Область определения и область значения Область определения и область значения]() Область определения и область значения
Область определения и область значения![Как найти область значения функции Как найти область значения функции]() Как найти область значения функции
Как найти область значения функции![Методика определение понятий Методика определение понятий]() Методика определение понятий
Методика определение понятий- Дайте определение понятию образование
![Что является определением понятия трансформаторная подстанция Что является определением понятия трансформаторная подстанция]() Что является определением понятия трансформаторная подстанция
Что является определением понятия трансформаторная подстанция
 Область определения сложной функции
Область определения сложной функции Функции нескольких переменных область определения линии уровня
Функции нескольких переменных область определения линии уровня Как обозначается область определения функции
Как обозначается область определения функции Какое краткое определение соответствует понятию государства
Какое краткое определение соответствует понятию государства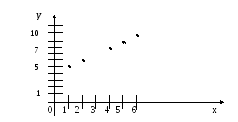 Область определения и область значения
Область определения и область значения Как найти область значения функции
Как найти область значения функции Методика определение понятий
Методика определение понятий Что является определением понятия трансформаторная подстанция
Что является определением понятия трансформаторная подстанция