3.1.1. Коэффициент корреляции для выборки и для генеральной совокупности
В качестве меры для степени линейной связи двух переменных используется коэффициент их корреляции.
 (3. 0)
(3. 0)
По формуле коэффициента корреляции видно, что он будет положителен, если отклонения переменных XиYот своих средних значении имеют, как правило, одинаковый знак, и отрицательным - если разные знаки.

Рис. 3.1. Типы зависимостей и коэффициент корреляции
Коэффициент корреляции является безразмерной величиной (так как размерности числителя и знаменателя есть размерности произведения ХY); его величина не зависит от выбора единиц измерения обеих переменных. Величина коэффициента корреляции меняется от -1 в случае строгой линейной отрицательной связи до +1 в случае строгой линейной положительной связи.
Для оценки значимости коэффициента корреляции можно воспользоваться следующей грубой оценкой:
![]() < 0,3 – линейная связь отсутствует;
< 0,3 – линейная связь отсутствует;
0,3 ![]() < 0,7 – имеется слабая линейная связь;
< 0,7 – имеется слабая линейная связь;
![]() 0,7 – имеется сильная линейная связь;
0,7 – имеется сильная линейная связь;
Случаи положительной и отрицательной корреляции переменных (с близкими по модулю к единице коэффициентами корреляции) показаны на рис. 3.1. Близкая к нулю величина коэффициента корреляции говорит об отсутствии линейной связи переменных, но не об отсутствии связи между ними вообще. Это ясно из правой части рис. 3.1, где Х иY,очевидно, связаны друг с другом (лежат на одной окружности), но их коэффициент корреляции близок к нулю. Последнее вытекает их того, что каждой паре одинаковых отклонений переменной X от ее среднего значения соответствуют равные по абсолютной величине положительное и отрицательное отклонения переменнойXот ее среднего. Соответственно, произведения этих отклонений "гасят" друг друга в числителе формулы коэффициента корреляции, и он оказывается близким к нулю. Заметим, что в числителе формулы для выборочного коэффициента корреляции величинХ иYстоит ихпоказатель ковариации:
 (3. 0)
(3. 0)
Этот показатель, как и коэффициент корреляции, характеризует степень линейной связи величин ХиY, и он также равен нулю, если эти величины независимы. Однако, в отличие от коэффициента корреляции, показатель ковариации не нормирован - он имеет размерность, и его величина зависит от единиц измерения величинХ иY.В статистическом анализе показатель ковариации сам по себе используется редко; он фигурирует обычно как промежуточный элемент расчета коэффициента корреляции.
Мы вели до сих пор речь о выборочном коэффициенте корреляции величин ХиY,который рассчитывается для оценки степени линейной связи этих величин по данным выборки. При этом истинным показателем степени линейной связи величинХ иYдля закона распределения, имеющегося на генеральной совокупности, является теоретический коэффициент корреляцииXY, оценкой которого является выборочный коэффициент корреляции. Коэффициент корреляции для генеральной совокупности определяется следующим образом:
![]() (3. 0)
(3. 0)
Стоящий в числителе этой формулы показатель ковариации величин XиYопределяется следующим образом:
Cov(X,Y)=M[(X-M[X]](Y-M[Y]] (3. 0)
Используя показатель ковариации, удобно записать формулу для дисперсии суммы случайных величин ХиY:
D[X+Y]=D[X]+D[Y]+2cov(X,Y) (3. 0)
Исходя из определения коэффициента корреляции, покажем, что он равен 1 или -1 при строгой линейной зависимости величин Х и Yи равен нулю в случае их независимости.
Пусть Y=а+bХ.Тогда
Cov[X,Y]=M[(X-M[X])(Y-M[Y])]= M[(X-M[X]](a+bX-M[a+bX])]=
= M[(X-M[X])(a+bX-M[a]-M[bX])]= M[(X-M[X])(a+bX-a-bM[X])]= M[(X-M[X])b(X-M[X])]= bD[X].
Очевидно также, что D[Y]=D[a+bX]=b2D[X], и ![]() , то есть коэффициент корреляции равен 1 при положительном коэффициентеb и равен -1 при отрицательномb.ЕслиХ иYнезависимы, то
, то есть коэффициент корреляции равен 1 при положительном коэффициентеb и равен -1 при отрицательномb.ЕслиХ иYнезависимы, то
Cov[X,Y]=M[(X-M[X])(Y-M[Y])]= M[X-M[X]]M[Y-M[Y]] = 00 = 0
но необязательно наоборот.
Итак, равный нулю коэффициент корреляции для генеральной совокупности говорит об отсутствии линейной связи рассматриваемых величин. Однако он не свидетельствует об отсутствии их связи вообще. В случае равенства нулю показателя корреляции, например, величин уровней инфляции и безработицы (а это действительно практически так для периода 1970-х - 1980-х годов для экономики США) нужно не говорить сразу о независимости этих показателей в данный период, а попытаться построить более сложную модель их связи, учитывающую, возможно, как нелинейность саой зависимости, так и наличие в ней запаздываний во времени (лагов), а также инерционность динамики соответствующих величин.
StudFiles.ru
Оценка существенности линейного коэффициента корреляции
В этой связи и возникает необходимость оценки существенности линейного коэффициента корреляции, дающая возможность распространить выводы по результатам выборки на генеральную совокупность. В зависимости от объема выборочной совокупности предлагаются различные методы оценки существенности линейного коэффициента корреляции. В отношении приводимых ниже критериев существенности можно сделать общее замечание, касающееся свойств исходной совокупности. Этим свойством является нормальное распределение значений признака в генеральной совокупности.
Рассмотрим следующие критерии:
1. При большом объеме выборки из нормально распределенной совокупности можно считать распределение линейного коэффициента корреляции приближенно нормальным со средней, равной r и дисперсией
 , (1.5)
, (1.5)
откуда средняя квадратическая ошибка коэффициента корреляции:
 , (1.6)
, (1.6)
где r – линейный коэффициент корреляции, n – объем выборки.
Если величина линейного коэффициента корреляции превышает величину средней квадратической ошибки более чем в tasr раза, то можно говорить о существенности выборочного коэффициента корреляции, где уровень значимости 0,01 или 0,05. Если же отношение
 ,
,
то с вероятностью (1 – a) следует предполагать отсутствие корреляционной связи в генеральной совокупности.
Доверительный интервал для коэффициента корреляции будет записан так:
 , (1.7)
, (1.7)
где rген – значение коэффициента корреляции в генеральной совокупности.
В нашем примере sr = 0,0787; при уровне значимости a = 0,05, и числе степеней свободы 20 – 2 = 18 ta = 2,1; интервал равен: 0,0787 × 2,1 = 0,1654 и пределы коэффициента корреляции: от 0,6451 до 0,9759.
При малых объемах выборки и линейном коэффициенте корреляции, близким к 1, использование средней квадратической ошибки по формуле (1.7) в качестве критерия существенности r оказывается невозможным в силу того, что распределение выборочного r может значительно отличаться от нормального.
2. Для малого объема выборочной совокупности используется тот факт, что величина

при условии r = 0, распределена по закону Стьюдента с (n –2) степенями свободы.
Полученную величину tрасч сравнивают с табличным значением t-критерия (число степеней свободы равно n –2). Если рассчитанная величина превосходит табличную, то практически невероятно, что найденное значение обусловлено только случайными совпадениями x и y в выборке из генеральной совокупности, для которой действительное значение коэффициента корреляции равно нулю. Если же вычисленная величина меньше, чем табличная, то полагают, что коэффициент корреляции в генеральной совокупности в действительности равен нулю и соответственно эмпирический коэффициент корреляции существенно не отличается от нуля.
Применим указанный метод к оценке существенности корреляции между уровнем затрат туристических фирм на рекламу и числом туристов, воспользовавшихся услугами фирм. При объеме выборки, равном 20 и при условии, что величина коэффициента корреляции равна 0,8105
 .
.
tтабл для числа степеней свободы 18 и уровня значимости 0,01 равно 2,878. Таким образом, лишь с вероятностью меньшей 1% можно утверждать, что величина t = 5,871 могла появиться в силу случайностей выборки. Такое событие является маловероятным и можно считать с вероятностью 99%, что в генеральной совокупности действительно существует прямая зависимость между изучаемыми признаками, т.е. отличие выборочного коэффициента корреляции от нуля является существенным.
3. Проверку гипотезы об отсутствии связи можно сделать и без вычисления расчетного значения критерия Стьюдента, пользуясь таблицей, составленной Р.Фишером. В этой таблице (Приложение 1) показывается величина коэффициента корреляции, которая может считаться существенной при данном количестве наблюдений (число степеней свободы равно n – 2).
В нашем примере находим по приложению 1, что коэффициент корреляции должен быть, по крайней мере, не ниже 0,5614 для того, чтобы он мог считаться существенным при уровне значимости a = 0,01 и не ниже 0,4438 при a = 0,05. По расчету коэффициент корреляции 0,8195, следовательно, между изучаемыми признаками существует прямая связь.
studopedia.ru
Проверка гипотезы о значимости выборочного коэффициента линейной корреляции
Это ответ на вопрос: существует ли вообще эта связь.
Эмпирический коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего ге  нерального параметра. Выборочный коэффициент линейной корреляции rв - величина случайная, так как он вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, а значит, как и любая случайная величина, имеет ошибку тr.
нерального параметра. Выборочный коэффициент линейной корреляции rв - величина случайная, так как он вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, а значит, как и любая случайная величина, имеет ошибку тr.
Чтобы выяснить, находятся ли случайные величины X и Y генеральной совокупности в линейной корреляционной зависимости, надо проверить значимость rв. Для этого проверяют нулевую гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности H0: rген = 0, то есть линейная корреляционная связь между признаками X и Y случайна. Выдвигается альтернативная гипотеза H1: rген ≠ 0, то есть эта линейная корреляционная связь имеется. Задается уровень значимости, например, α ≤ 0,05.
Критерием для проверки нулевой гипотезы является отношение выборочного коэффициента корреляции к своей ошибке:

где тr - ошибка коэффициента корреляции.
Если объем выборки п < 100, то  ;
;
если объем выборки п > 100, то  .
.
Число степеней свободы для проверки критерия равно f = п - 2. Гипотезу проверяют по таблицам распределения Стьюдента в соответствии с выбранным уровнем значимости.
По таблице критических точек распределения Стьюдента находим tкрит (α, f), определенное на уровне значимости α ≤ 0,05 при числе степеней свободы f = п - 2, где n - объем двумерной выборки.
Если tнабл > tкрит => H1- отвергают нулевую гипотезу и принимают альтернативную: rген ≠ 0, имеется линейная корреляционная связь между признаками.
Если tнабл < tкрит - то нет оснований отвергать нулевую гипотезу, а rв статистически незначим. Эта связь случайна.
Проверить значимость коэффициента корреляции r = 0,74 между переменными X и Y для выборки объема n = 50.
Решение:
Проверяется нулевая гипотеза H0 об отсутствии линейной корреляционной связи между переменными X и Y в генеральной совокупности H0: rген = 0.
При справедливости этой гипотезы  , где ошибка коэффициента корреляции
, где ошибка коэффициента корреляции  и
и  имеют распределение Стьюдента сf = n-2 степенями свободы.
имеют распределение Стьюдента сf = n-2 степенями свободы.
Рассчитаем:  .
.
По таблицам находим табличное значение t-критерия Стьюдента, определенное на уровне значимости α ≤ 0,05 и при числе степеней свободы f = 50 - 2 = 48, tкрит(α ≤ 0,05; 48) = 2,02.
Поскольку tнабл > tкрит, 7,62 > 2,02, коэффициент корреляции значимо отличается от нуля.
Причем это справедливо и для уровня значимости:
α ≤ 0,001 (t = 3,55).
По выборке объема п = 122, извлеченной из нормальной двумерной совокупности (X, Y), найден выборочный коэффициент линейной корреляции r = 0,4. При уровне значимости α ≤ 0,05 проверить нулевую гипотезу H0, которая заключается в том, что связь между признаками случайна.
Решение:


Сравниваем: tнабл > tкрит (α, f), 5,24 > 1,98 => H1 – отвергается нулевая гипотеза.
Вывод: имеется умеренная линейная корреляционная связь между признаками: r = 0,4 (α ≤ 0,05).
studopedia.ru
Вопросы. Тема 3. Парная регрессия и корреляция[2]. статистическая зависимость (независимость) случайных переменных
Тема 3. Парная регрессия и корреляция[2].
- статистическая зависимость (независимость) случайных переменных. Ковариация.
- Анализ линейной статистической связи экономических данных, корреляция; вычисление коэффициентов корреляции.
- линейная модель парной регрессии.
- Оценка параметров модели с помощью метода наименьших квадратов (МНК).
- Оценка существенности параметров линейной регрессии.
- Интервалы прогноза по линейному уравнению регрессии.
Материал данной темы частично знаком студентам и подробно изложен в учебном пособии [1] стр. 170 -176 и 190 - 207.
Рассматривая зависимости между признаками, необходимо выделить, прежде всего, две категории зависимости: 1) функциональные и 2) корреляционные.
Функциональные связи характеризуются полным соответствием между изменением факторного признака и изменением результативной величины, и каждому значению признака-фактора соответствуют вполне определенные значения результативного признака. Функциональная зависимость может связывать результативный признак с одним или несколькими факторными признаками. Так, величина начисленной заработной платы при повременной оплате труда зависит от количества отработанных часов.
В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных. Одновременное воздействие на изучаемый признак большого количества самых разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу и направленность своего воздействия.
Основная задача корреляционного анализа заключается в выявлении взаимосвязи между случайными переменными путем точечной и интервальной оценки парных (частных) коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации. Кроме того, с помощью корреляционного анализа решаются следующие задачи: отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связи между ними; обнаружение ранее неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между параметрами, но устанавливает численное значение этих связей и достоверность суждений об их наличии.
При проведении корреляционного анализа вся совокупность данных рассматривается как множество переменных (факторов), каждая из которых содержит n –наблюдений.
При изучении взаимосвязи между двумя факторами их, как правило, обозначают X=  и Y=
и Y=
.
ковариация - это статистическая мера взаимодействия двух переменных.
Например, положительное значение ковариации доходности двух ценных бумаг показывает, что доходности этих ценных бумаг имеют тенденцию изменяться в одну сторону.
Ковариация между двумя переменными  рассчитывается следующим образом:
рассчитывается следующим образом:
 ,
,
где  - фактические значения случайных переменных x и y,
- фактические значения случайных переменных x и y,
 .
. 
Ковариация зависит от единиц, в которых измеряются переменные  .
.
Поэтому для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции.
Вычисление коэффициента парной корреляции.
Коэффициент парной корреляции
Для двух переменных  коэффициент парной корреляции определяется следующим образом:
коэффициент парной корреляции определяется следующим образом:
 =
=  , (1)
, (1)
где 
 - оценки дисперсий величин
- оценки дисперсий величин  .
.
Дисперсия (оценка дисперсии)

характеризуют степень разброса значений  (
( ) вокруг своего среднего
) вокруг своего среднего  (
( , соответственно), или вариабельность (изменчивость) этих переменных на множестве наблюдений.
, соответственно), или вариабельность (изменчивость) этих переменных на множестве наблюдений.
В общем случае для получения несмещенной оценки дисперсии сумму квадратов следует делить на число степеней свободы оценки (n−p), где n - объем выборки, p - число наложенных на выборку связей. В данном случае p = 1, т.к. выборка уже использовалась один раз для определения среднего X, поэтому число наложенных связей равно единице, а число степеней свободы оценки (т.е. число независимых элементов выборки) равно (n −1).
Более естественно измерять степень разброса значений переменных в тех же единицах, в которых измеряется и сама переменная. Эту задачу решает показатель, называемый среднеквадратическим отклонением или стандартным отклонением, или стандартной ошибкой переменной Х (переменной Y), определяемый соотношением:

Слагаемые в числителе формулы (1) выражают взаимодействие двух переменных и определяют знак (положительной или отрицательной) корреляции. Если, например, между переменными существует сильная положительная взаимосвязь (увеличение одной переменной при увеличении второй), каждое слагаемое будет положительным числом. Аналогично, если между переменными существует сильная отрицательная взаимосвязь, все слагаемые в числителе будут отрицательными числами, что в результате дает отрицательное значение корреляции.
Знаменатель выражения для коэффициента корреляции просто нормирует числитель таким образом, что коэффициент корреляции оказывается легко интерпретируемым числом, не имеющим размерности, в диапазоне от -1 до 1.
Числитель выражения для коэффициента корреляции, который трудно интерпретировать из-за необычных единиц измерения, называется ковариацией Х и Y. Несмотря на то, что иногда он используется как самостоятельная характеристика (например, в теории финансов для описания совместного изменения курсов акций на двух биржах), удобнее пользоваться коэффициентом корреляции. Корреляция и ковариация представляют, по сути, одну и ту же информацию, однако корреляция представляет эту информацию в более удобной форме.
Следует отметить, что величина коэффициента корреляции не является доказательством наличия причинно-следственной связи между исследуемыми признаками, а является оценкой степени взаимной согласованности в изменениях признаков. Установлению причинно-следственной зависимости предшествует анализ качественной природы явлений. Но есть и еще одно обстоятельство, объясняющее формулировку выводов о возможном наличии связи по величине коэффициента корреляции.
Связано это с тем, что оценка степени тесноты связи с помощью коэффициента корреляции производится, как правило, на основе более или менее ограниченной информации об изучаемом явлении. Возникает вопрос, насколько правомерно наше заключение по выборочным данным в отношении действительного наличия корреляционной связи в той генеральной совокупности, из которой была произведена выборка?
Принципиально возможны случаи, когда отклонение от нуля полученной величины выборочного коэффициента корреляции оказывается целиком, обусловленным неизбежными случайными колебаниями тех выборочных данных, на основании которых он вычислен. Особенно осторожно следует подходить к истолкованию полученных коэффициентов корреляции при незначительных объемах выборочной совокупности.
В этой связи и возникает необходимость оценки существенности линейного коэффициента корреляции, дающая возможность распространить выводы по результатам выборки на генеральную совокупность. В зависимости от объема выборочной совокупности предлагаются различные методы оценки существенности линейного коэффициента корреляции.
Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием t - критерия Стьюдента. При этом фактическое (наблюдаемое) значение этого критерия определяется по формуле:

Вычисленное по этой формуле значение tнабл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-2).
Если tнабл > tкр, то полученное значение коэффициента корреляции признается значимым (то есть нулевая гипотеза, утверждающая равенство нулю генерального коэффициента корреляции, отвергается). И таким образом делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
Удобным графическим средством анализа парных данных является диаграмма рассеяния, которая представляет каждое наблюдение в пространстве двух измерений, соответствующих двум факторам.
Диаграмму рассеяния, на которой изображается совокупность значений двух признаков, называют еще корреляционным полем. Каждая точка этой диаграммы имеет координаты Xi и Yi. По мере того, как возрастает сила линейной связи, точки на графике будут лежать более близко к прямой линии, а величина r будет ближе к 1.
Парная регрессия
Регрессионный анализ[3] занимает ведущее место в математике статистических методах эконометрики. До регрессионного анализа следует проводить корреляционный анализ, в процессе которого оценивается степень тесноты статистической связи между исследуемыми переменными. От степени тесноты связи зависит прогностическая сила регрессионной модели.
Регрессионный анализ предназначен для исследования зависимости исследуемой переменной от различных факторов и отображения их взаимосвязи в форме регрессионной модели.
В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции f ( ), где
), где  - независимые (объясняющие) переменные, или факторы.
- независимые (объясняющие) переменные, или факторы.
Связь между переменной Y иk независимыми факторами Х можно охарактеризовать функцией регрессии Y= f ( ), которая показывает, каково будет в среднем значение переменной yi, если переменные Xi примут конкретные значения.
), которая показывает, каково будет в среднем значение переменной yi, если переменные Xi примут конкретные значения.
Данное обстоятельство позволяет использовать модель регрессии не только для анализа, но и для прогнозирования экономических явлений.
Сформулируем регрессионную задачу для случая одного факторного признака.
Пусть имеется набор значений двух переменных: Y= - объясняемая переменная и X=
- объясняемая переменная и X=  - объясняющая переменная, каждая из которых содержит n наблюдений.
- объясняющая переменная, каждая из которых содержит n наблюдений.
Пусть между переменными X=  и Y=
и Y= теоретически существует некоторая линейная зависимость
теоретически существует некоторая линейная зависимость
 .
.
Данное уравнение будем называть «истинным» уравнением регрессии.
Однако в действительности между X и Y наблюдается не столь жесткая связь. Отдельные наблюдения  будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и не известных исследователю, а также случайных причин (возмущения и помехи); существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи, естественно, могут возникнуть и в силу неправильного выбора вида самого уравнения, описывающего эту зависимость. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде
будут отклоняться от линейной зависимости в силу воздействия различных причин. Обычно зависимая переменная находится под влиянием целого ряда факторов, в том числе и не известных исследователю, а также случайных причин (возмущения и помехи); существенным источником отклонений в ряде случаев являются ошибки измерения. Отклонения от предполагаемой формы связи, естественно, могут возникнуть и в силу неправильного выбора вида самого уравнения, описывающего эту зависимость. Учитывая возможные отклонения, линейное уравнение связи двух переменных (парную регрессию) представим в виде
 , (2)
, (2)
где  - постоянная величина (или свободный член уравнения),
- постоянная величина (или свободный член уравнения),  - коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной
- коэффициент регрессии, определяющий наклон линии, вдоль которой рассеяны данные наблюдений. Это показатель, характеризующий изменение переменной  , при изменении значения
, при изменении значения  на единицу. Если
на единицу. Если  - переменные
- переменные  и
и  положительно коррелированные, если
положительно коррелированные, если  < 0 – отрицательно коррелированны;
< 0 – отрицательно коррелированны;  - случайная переменная, или случайная составляющая, или остаток, или возмущение. Она отражает тот факт, что изменение
- случайная переменная, или случайная составляющая, или остаток, или возмущение. Она отражает тот факт, что изменение  будет неточно описываться изменением Х – присутствуют другие факторы, неучтенные в данной модели.
будет неточно описываться изменением Х – присутствуют другие факторы, неучтенные в данной модели.
Таким образом, в уравнении (2) значение каждого наблюдения  представлено как сумма двух частей — систематической
представлено как сумма двух частей — систематической  и случайной
и случайной  . В свою очередь систематическую часть можно представить в виде уравнения
. В свою очередь систематическую часть можно представить в виде уравнения

Можно сказать, что общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части — объясненную и случайную.
 .
.
studopedia.ru
Читайте также
![Коэффициент корреляции может принимать значения Коэффициент корреляции может принимать значения]() Коэффициент корреляции может принимать значения
Коэффициент корреляции может принимать значения![Значения коэффициентов корреляции графиков нагрузки потребителей Значения коэффициентов корреляции графиков нагрузки потребителей]() Значения коэффициентов корреляции графиков нагрузки потребителей
Значения коэффициентов корреляции графиков нагрузки потребителей![Значение коэффициента корреляции Значение коэффициента корреляции]() Значение коэффициента корреляции
Значение коэффициента корреляции![Акт определение Акт определение]() Акт определение
Акт определение- Актив определение
![База данных определение База данных определение]() База данных определение
База данных определение![Бетон определение Бетон определение]() Бетон определение
Бетон определение![Власть определение Власть определение]() Власть определение
Власть определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Газоопасные работы определение Газоопасные работы определение]() Газоопасные работы определение
Газоопасные работы определение![Генетическое определение пола кратко Генетическое определение пола кратко]() Генетическое определение пола кратко
Генетическое определение пола кратко![Генетические механизмы определения пола Генетические механизмы определения пола]() Генетические механизмы определения пола
Генетические механизмы определения пола
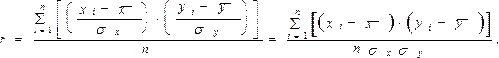 Коэффициент корреляции может принимать значения
Коэффициент корреляции может принимать значения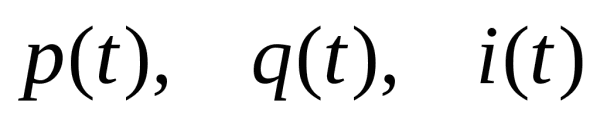 Значения коэффициентов корреляции графиков нагрузки потребителей
Значения коэффициентов корреляции графиков нагрузки потребителей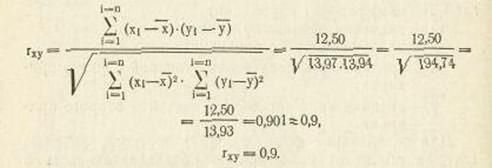 Значение коэффициента корреляции
Значение коэффициента корреляции Акт определение
Акт определение База данных определение
База данных определение Бетон определение
Бетон определение Власть определение
Власть определение Болезнь определение
Болезнь определение Газоопасные работы определение
Газоопасные работы определение Генетическое определение пола кратко
Генетическое определение пола кратко Генетические механизмы определения пола
Генетические механизмы определения пола