Определение обратной функции

Обратная функция

Не следует путать с Обратная величина.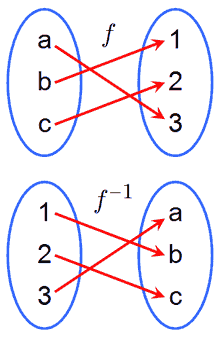

Функция f {\displaystyle f} и обратная ей функция f − 1 {\displaystyle f^{-1}} . Если f ( a ) = 3 {\displaystyle f(a)=3} , то f − 1 ( 3 ) = a {\displaystyle f^{-1}(3)=a}

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f {\displaystyle f} обычно обозначается f − 1 {\displaystyle f^{-1}} , иногда также используется обозначение f i n v {\displaystyle f^{\mathrm {inv} }} .

Определение

Функция g : Y → X {\displaystyle g:Y\to X} является обратной к функции f : X → Y {\displaystyle f:X\to Y} , если выполнены следующие тождества:

f ( g ( y ) ) = y {\displaystyle f(g(y))=y} для всех y ∈ Y ; {\displaystyle y\in Y;}
g ( f ( x ) ) = x {\displaystyle g(f(x))=x} для всех x ∈ X . {\displaystyle x\in X.}

Существование

Чтобы найти обратную функцию, нужно решить уравнение y = f ( x ) {\displaystyle y=f(x)} относительно x {\displaystyle x} . Если оно имеет более чем один корень, то функции, обратной к f {\displaystyle f} не существует. Таким образом, функция f ( x ) {\displaystyle f(x)} обратима на интервале ( a ; b ) {\displaystyle (a;b)} тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F ( y ) {\displaystyle F(y)} выразить y {\displaystyle y} из уравнения x − F ( y ) = 0 {\displaystyle x-F(y)=0} возможно в том и только том случае, когда функция F ( y ) {\displaystyle F(y)} строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, x {\displaystyle {\sqrt {x}}} является обратной функцией к x 2 {\displaystyle x^{2}} на [ 0 , + ∞ ) {\displaystyle [0,+\infty )} , хотя на промежутке ( − ∞ , 0 ] {\displaystyle (-\infty ,0]} обратная функция другая: − x {\displaystyle -{\sqrt {x}}} .

Примеры

Если F : R → R + , F ( x ) = a x {\displaystyle F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}} , где a > 0 , {\displaystyle a>0,} то F − 1 ( x ) = log a ⁡ x . {\displaystyle F^{-1}(x)=\log _{a}x.}
Если F ( x ) = a x + b , x ∈ R {\displaystyle F(x)=ax+b,\;x\in \mathbb {R} } , где a , b ∈ R {\displaystyle a,b\in \mathbb {R} } фиксированные постоянные и a ≠ 0 {\displaystyle a\neq 0} , то F − 1 ( x ) = x − b a . {\displaystyle F^{-1}(x)={\frac {x-b}{a}}.}
Если F ( x ) = x n , x ≥ 0 , n ∈ Z {\displaystyle F(x)=x^{n},x\geq 0,n\in \mathbb {Z} } , то F − 1 ( x ) = x n . {\displaystyle F^{-1}(x)={\sqrt[{n}]{x}}.}

Свойства

Областью определения F − 1 {\displaystyle F^{-1}} является множество Y {\displaystyle Y} , а областью значений — множество X {\displaystyle X} .
По построению имеем:

y = F ( x ) ⇔ x = F − 1 ( y ) {\displaystyle y=F(x)\Leftrightarrow x=F^{-1}(y)}

или

F ( F − 1 ( y ) ) = y , ∀ y ∈ Y {\displaystyle F\left(F^{-1}(y)\right)=y,\;\forall y\in Y} , F − 1 ( F ( x ) ) = x , ∀ x ∈ X {\displaystyle F^{-1}(F(x))=x,\;\forall x\in X} ,

или короче

F ∘ F − 1 = i d Y {\displaystyle F\circ F^{-1}=\mathrm {id} _{Y}} , F − 1 ∘ F = i d X {\displaystyle F^{-1}\circ F=\mathrm {id} _{X}} ,

где ∘ {\displaystyle \circ } означает композицию функций, а i d X , i d Y {\displaystyle \mathrm {id} _{X},\mathrm {id} _{Y}} — тождественные отображения на X {\displaystyle X} и Y {\displaystyle Y} соответственно.

Функция F {\displaystyle F} является обратной к F − 1 {\displaystyle F^{-1}} :

( F − 1 ) − 1 = F {\displaystyle \left(F^{-1}\right)^{-1}=F} .

Пусть F : X ⊂ R → Y ⊂ R {\displaystyle F:X\subset \mathbb {R} \to Y\subset \mathbb {R} } — биекция. Пусть F − 1 : Y → X {\displaystyle F^{-1}:Y\to X} её обратная функция. Тогда графики функций y = F ( x ) {\displaystyle y=F(x)} и y = F − 1 ( x ) {\displaystyle y=F^{-1}(x)} симметричны относительно прямой y = x {\displaystyle y=x} .

Разложение в степенной ряд

Обратная функция аналитической функции может быть представлена в виде степенного ряда:

F − 1 ( y ) = ∑ k = 0 ∞ A k ( x 0 ) ( y − f ( x 0 ) ) k k ! , {\displaystyle F^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},}

где коэффициенты A k {\displaystyle A_{k}} задаются рекурсивной формулой:

A k ( x ) = { A 0 ( x ) = x A n + 1 ( x ) = A n ′ ( x ) F ′ ( x ) {\displaystyle A_{k}(x)={\begin{cases}A_{0}(x)=x\\A_{n+1}(x)={\frac {A_{n}'(x)}{F'(x)}}\end{cases}}}

ru.wikipedia.org

/ матан коллоквиум / 7.Понятие сложной обратной функции

Понятие о сложной функцииПусть даны две функцииz = f(y)и у = g(x). Сложной функцией (или композицией функций f иg)

называется функция z = h(x), значения которой вычисляются по правилуh(x) = f(g(x))

(т. е. сначала вычисляется g(x), при этом получается некоторое числоу, а затем вычисляется

значение в точке у).

Пример.Функцию можно рассматривать как композицию функций и.

Для записи композиции функций употребляется значок . Например, записьозначает,

что функция hполучена как композиция функцийfиg(сначала применяетсяg, а затемf),

т. е. . Операция образования сложной функции (или композиция функций) не обладает переместительным

свойством: . Чтобы можно было вычислить сложную функциюh = f(g(x)), надо, чтобы числоg(x), т. е.

значение функции g, попадало в область определения функцииf.

Пример.Вычисляя значения функции, необходимо брать только те числах,

для которых , т. е. те, для которых числопопадает в область определения функции

Взаимно обратные функцииПусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x)можно переменную х

однозначно выразить через переменную у.Выразив хчерез у, мы получим равенство вида х = g(y).

В этой записи gобозначает функцию, обратную кf. Если функцияgявляется обратной для функцииf, то и функция является обратной для функцииg. Пару функцийfиgназывают взаимно обратными функциями.

График обратной функцииЕсли мы одновременно построим графики функцийf иgв одной и той же системе координат,
откладывая по оси абсцисс аргументы обеих функций, а по оси ординат –их значения,
то эти графики будут симметричны друг другу относительно прямой у = х.

4. Свойства взаимно обратных функцийОтметим некоторые свойства взаимно обратных функций. 1)Тождества. Пустьfиg–взаимно обратные функции. Тогда : f(g(y)) = уиg(f(x)) = х. 2)Область определения. Пусть fиg –взаимно обратные функции. Область определения функцииf

совпадает с областью значений функции g, и наоборот, область значений функции fсовпадает с

областью определения функции g. 3)Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает.

Аналогичное утверждение верно и для убывающих функций. 4) Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат,

симметричны друг другу относительно прямойу = х.

StudFiles.ru

Обратная функция это:

Обратная функция Функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у, х = φ (y), является обратной по отношению к данной функции у = f (x). Например, О. ф. для у = ax + b (а≠0) является х = (у—b)/a, О. ф. для у = ех является х = ln у и т.д. Если х = φ(y) есть О. ф. по отношению к у = f (x), то и у = f (x) есть О. ф. по отношению к х = φ(y). Областью определения О. ф. является область значений данной функции, а областью значений О. ф.— область определения данной. Графики двух взаимно обратных функций у = f (x) и у = φ (x) (где независимое переменное обозначено одной и той же буквой х), как, например, у = ax + b и у = (х—b)/a, у = ех и у = ln х, симметричны по отношению к биссектрисе у = х первого и третьего координатных углов. Функция, обратная по отношению к однозначной функии, может быть многозначной (ср., например, функции х2 и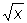

= f (x) принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). О. ф. по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна. Если данная функция кусочно монотонна, то, разбивая область её определения на участки её монотонности, получают однозначные ветви О. ф. Так, одним из участков монотонности для sin х служит интервал — π/2< x < π/2; ему соответствует т. н. главная ветвь arc sin х обратной функции Arc sin х. Для пары однозначных взаимно обратных функций имеют место соотношения φ[f (x)]=x и f [φ(x)] = х, первое из которых справедливо для всех значений х из области определения функции f (x), а второе — для всех значений х из области определения функции φ (x); например, elnx = х (х > 0), 1n (ex) = х (— ∞ < х < ∞). Иногда функцию, обратную к f (x) =у, обозначают f- -1(y) = х, так что для непрерывной и монотонной функции f (x): F -1[f (x)]=f [f -1) x)]=x. Вообще же f --1[f (x)] представляет собой многозначную функцию от х, одним из значений которой является х; так, для f (x) = x2, х (≠ 0) является лишь одним из двух значений f --1[f (x)] = √x2 (другое: —х); для f (x) = sin х, х является лишь одним из бесконечного множества значений f- -1[f (x)] = Arc sin [sin x] = (—1) n x + nπ, n = 0, ± 1, ± 2,.... Если у = f (x) непрерывна и монотонна в окрестности точки х = x₀ и дифференцируема при х = x₀, причём f'(x₀) ≠ 0, то f --1(y) дифференцируема при у = у₀ и

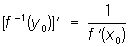(формула дифференцирования О. ф.). Так, для —π/2 < х π/2, у = f (x) = sin х непрерывна и монотонна, f’(x) = cos х ≠ 0 и f- -1(y)= arc sin у (—1< y где имеется в виду положительное значение корня (так как cos х > 0 для —π/2 < х π/2).

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

dic.academic.ru

Обратимая функция

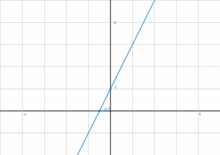График линейной функции, которая является обратимой.

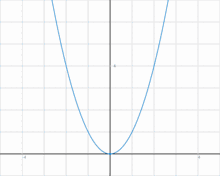График квадратичной функции, которая не является обратимой.

Обратимая функция — это функция, которая принимает каждое своё значение в единственной точке области определения.

Определение

Если функция y = f ( x ) {\displaystyle y=f(x)} такова, что для любого её значения y 0 {\displaystyle y_{0}} уравнение f ( x ) = y 0 {\displaystyle f(x)=y_{0}} имеет относительно x {\displaystyle x} единственный корень, то говорят, что функция f {\displaystyle f} обратима.

Свойства

Если функция y = f ( x ) {\displaystyle y=f(x)} определена и возрастает (или убывает) на промежутке X {\displaystyle X} и областью её значений является промежуток Y {\displaystyle Y} , то у неё существует обратная функция, причём обратная функция определена и возрастает (или убывает) на X {\displaystyle X} .[1]
Если функция y = f ( x ) {\displaystyle y=f(x)} задана формулой, то для нахождения обратной к ней функции нужно решить уравнение f ( x ) = y {\displaystyle f(x)=y} относительно x {\displaystyle x} , а потом поменять местами x {\displaystyle x} и y {\displaystyle y} .
Если уравнение f ( x ) = y {\displaystyle f(x)=y} имеет более одного корня, то функции, обратной функции y = f ( x ) {\displaystyle y=f(x)} , не существует.
Графики обратных функций симметричны относительно прямой y = x {\displaystyle y=x} .
Если f {\displaystyle f} и g {\displaystyle g} – функции, обратные друг другу, то E ( f ) = D ( g ) {\displaystyle E(f)=D(g)} , D ( f ) = E ( g ) {\displaystyle D(f)=E(g)} , где D {\displaystyle D} и E {\displaystyle E} – области определения и значений соответственно.
Обратная функция может существовать только для обратимой функции.

Примеры

Функция y = x 2 {\displaystyle y=x^{2}} не является обратимой на R {\displaystyle \mathbb {R} } , но обратима при x ⩾ 0 {\displaystyle x\geqslant 0} или x ⩽ 0 {\displaystyle x\leqslant 0} .
Функция sin ⁡ x {\displaystyle \sin x} не является обратимой на R {\displaystyle \mathbb {R} } , т. к. одному значению функции соответствует бесконечное множество значений аргумента.

ru.wikipedia.org

Что такое Обратная функция?

Олег комаров

Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией. Предположим, мы имеем функцию:
v = u^2 , где u - аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v :
u=sqrt(v).
Если обозначить аргумент в обеих функциях через x , а функцию – через y, то мы имеем две функции:
y=x^2 и y=sqrt(x), каждая из которых является обратной по отношению к другой.
П р и м е р ы . Эти функции являются обратными друг к другу:
1) sin x и Arcsin x, так как, если y = sin x, то x = Arcsin y;
2) cos x и Arccos x, так как, если y = cos x, то x = Arccos y;
3) tan x и Arctan x, так как, если y = tan x, то x = Arctan y;
4) e^x и ln x, так как, если y = e^x , то x = ln y.
http://www.bymath.net/studyguide/fun/sec/fun7.htm

Обратная функция, функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) - данная функция, то переменная х, рассматриваемая как функция переменной у, х = j (y), является обратной по отношению к данной функции у = f (x). Например, Обратная функция для у = ax + b (а¹0) является х = (у-b)/a, Обратная функция для у = ех является х = ln у и т.д. Если х = j(y) есть Обратная функция по отношению к у = f (x), то и у = f (x) есть Обратная функция по отношению к х = j(y). Областью определения Обратная функция является область значений данной функции, а областью значений Обратная функция- область определения данной. Графики двух взаимно обратных функций у = f (x) и у = j (x) (где независимое переменное обозначено одной и той же буквой х), как, например, у = ax + b и у = (х-b)/a, у = ех и у = ln х, симметричны по отношению к биссектрисе у = х первого и третьего координатных углов. Функция, обратная по отношению к однозначной функии, может быть многозначной (ср., например, функции х2 и ). Для однозначности Обратная функция необходимо и достаточно, чтобы данная функция у = f (x) принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). Обратная функция по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна.

Если данная функция кусочно монотонна, то, разбивая область её определения на участки её монотонности, получают однозначные ветви Обратная функция Так, одним из участков монотонности для sin х служит интервал - p/2< x < p/2; ему соответствует т. н. главная ветвь arc sin х обратной функции Arc sin х. Для пары однозначных взаимно обратных функций имеют место соотношения j[f (x)]=x и f [j(x)] = х, первое из которых справедливо для всех значений х из области определения функции f (x), а второе - для всех значений х из области определения функции j (x); например, elnx = х (х > 0), 1n (ex) = х (- ¥ < х < ¥). Иногда функцию, обратную к f (x) =у, обозначают f- -1(y) = х, так что для непрерывной и монотонной функции f (x):
F -1[f (x)]=f [f -1) x)]=x.
Вообще же f --1[f (x)] представляет собой многозначную функцию от х, одним из значений которой является х; так, для f (x) = x2, х (¹ 0) является лишь одним из двух значений f --1[f (x)] = √x2 (другое: -х); для f (x) = sin х, х является лишь одним из бесконечного множества значений
f- -1[f (x)] = Arc sin [sin x] = (-1) n x + np,
n = 0, ± 1, ± 2,...
Если у = f (x) непрерывна и монотонна в окрестности точки х = x0 и дифференцируема при х = x0, причём f"(x0) ¹ 0, то f --1(y) дифференцируема при у = у0 и
(формула дифференцирования Обратная функция). Так, для -p/2 < х < p/2, у = f (x) = sin х непрерывна и монотонна, f’(x) = cos х ¹ 0 и f- -1(y)= arc sin у (-1< y http://bse.sci-lib.com/article083236.html