Определение угловой скорости

Угловая скорость. Формула угловой скорости

Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие – скорость. И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч - значит за один час проехать 100 километров.

А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды – Солнца - делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!

Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?

Понятие угловой скорости

Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).

Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» - ω.

Классическая формула угловой скорости вращения рассматривается так.

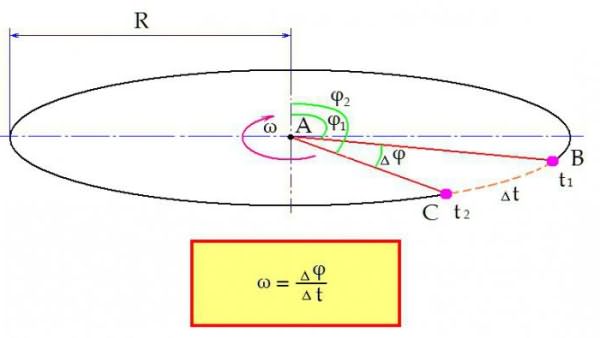
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.

Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:

∆t = t2 – t1.

Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:

∆φ = φ2 – φ1.

Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.

Единицы измерения угловой скорости

Скорость движения тела линейная измеряется в разных величинах. Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы – морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.

Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.

Радианы в секунду (рад/с) – классическое мерило скорости в международной системе единиц (СИ). Показывают – на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.

Обороты в минуту (об/мин) – самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.

Обороты в секунду (об/с) – используется реже, прежде всего в образовательных целях.

Период обращения

Иногда для определения скорости вращения удобнее пользоваться другим понятием. Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:

ω = 2П / Т.

Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.

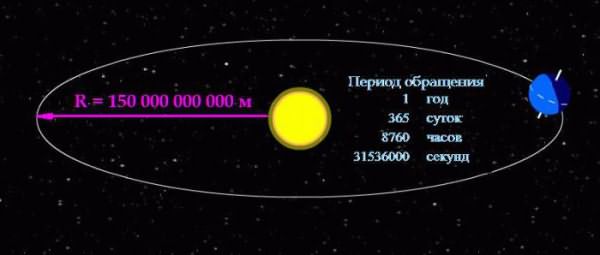
Формула угловой скорости позволяет вычислить её, зная период обращения:

ω = 2П/31536000 = 0,000000199238499086111 рад/с.

Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.

Связь угловой и линейной скоростей

В некоторых задачах должны быть определены линейная и угловая скорость. Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.

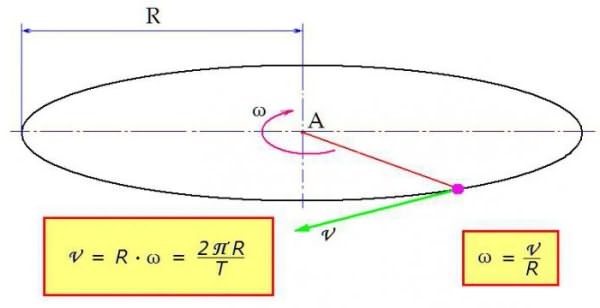
«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.

syl.ru

Угловая скорость

ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.

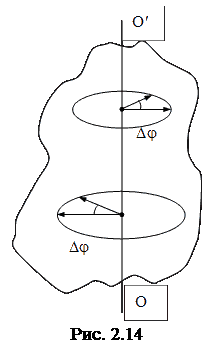В качестве координаты, определяющей положение точки при вращательном движении, берут угол, характеризующий мгновенное положение радиус-вектора, проведенного из центра вращения к рассматриваемой точке (рис. 2.14)

Для характеристики вращательного движения вводится понятие угловой скорости

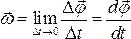Вектор 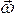направлен вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта (рис. 2.15).

Модуль вектора угловой скорости равен 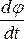. Если 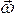= const, то такое движение называется равномерным, при этом 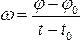, следовательно 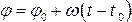и при t₀ = 0 получаем .

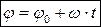Если j₀ = 0, то j = w·t или .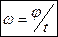

Таким образом, при равномерном движении w показывает на какой угол поворачивается тело за единицу времени. Размерность угловой скорости [w]=рад/сек.

Равномерное вращение можно характеризовать периодом вращения T, под которым понимают время, за которое тело делает один полный оборот, т.е. поворачивается на угол 2p. В этом случае 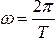, следовательно .

Частота вращения (число оборотов в единицу времени): n=1/T=w/2p. Отсюда w=2pn.

Дополнение 1.

Поворот тела на некоторый малый угол dj можно задать в виде отрезка, длина которого равна dj, а направление совпадает с осью, вокруг которой совершен поворот. Таким образом, повороту тела можно приписать некоторое численное значение и направление. При этом направление вектора можно определить, связав его с направлением вращения тела. Такие вектора называются аксиальными или псевдовекторами, в отличие от истинных или полярных векторов, для которых направление определяется естественным образом ( 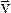, , 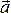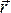и т. д.), при операции инверсии системы координат(x → -x’, y → -y’, z → -z’) последние меняют знак на противоположный: .

studopedia.ru

Вращательное движение и угловая скорость твердого тела

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

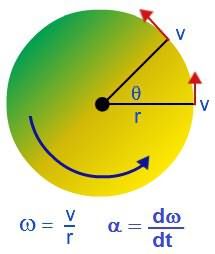
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек - сложно.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

φ = φ(t).

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной - угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с2.

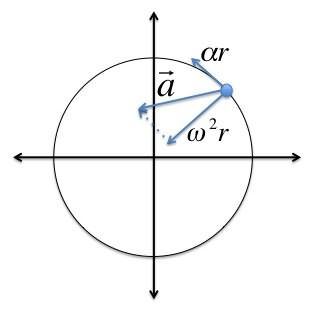
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ₀ + ωt, где φ₀ – начальное значение угла поворота.

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω₀+ εt, φ = φ₀ + ω₀t + εt2/2.

Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц = v2/R = (ωR)2/R = ω2R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

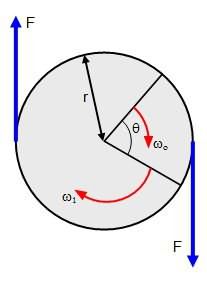
Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα,где α - угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R2mβ, β= M/mR2 = M/I, где I = mR2 - момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•104 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Решение

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω₀ - εt.

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω₀/t = 2πn/t.

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с2).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ₀ + ω₀t + εt2/2. Учитывая выражение для углового ускорения и то, что φ₀ = 0, находим: φ(t)= ω₀t/2 = πnt.

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•104 (об.).

Ответ: угловое ускорение равно 4,36 рад/с2; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•104 об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Решение

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR2 = F/mR.

Найдем время, за которое диск остановится: t = ω₀/ε, где ω₀ - начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

syl.ru

Определение линейных скоростей всех точек механизма и угловых скоростей звеньев

Исходные данные:

φ = 3300;

n= 95 min-1;

l_AB= 0.07 м;

l_BC= 0.44 м;

l_CF= 0.53 м;

l_CD= 0.31 м;

l_EF= 0.38 м;

m₁= 4 кг;

m₂= 6 кг;

m₃= 7 кг;

m₄ = 5 кг;

m₅= 11 кг;

центры масс всех звеньев лежат посредине длинны.

Линейные скорости точек и угловые скорости звеньев необходимы для вычисления кинетической энергии механизма, определения его инертных свойств. Скорости могут быть определены различными способами, из которых наиболее распространены два способа: при помощи МЦС и метод планов скоростей.

При помощи МЦС

Определим угловую скорость вращения кривошипа:

Определим линейную скорость точки А:

Вектор направлен перпендикулярно звену АB по направлению .

Звено СD совершает вращательное движение, значит скорость точки C направлена перпендикулярно звену СD. Для звена ВC, совершающего плоскопараллельное движение , находим МЦС. Для этого восстанавливаем перпендикуляры к направлениям скоростей и. Их пересечение является МЦС звена ВC (Р₂). На звене отмечаем середину – точку S₂ – и соединяем с полюсом Р₂. Угловая скорость звена 2 будет описываться соотношением:

Где BР₂=800 мм (замеряем на чертеже);

CР₂= 648 мм, S₂P₂=694 мм.

Учитывая масштаб построения, имеем:

Определяем скорости:

Определяем скорость :

Угловая скорость звена CF:

Далее определяем МЦС для звена 4. Учитывая, что ползун 5 движется только горизонтально, восстанавливаем перпендикуляры к направлениям скоростей и, и получаем точку Р₄ удалённую на значительное растояние

Для определения направления скорости соединяем точкуS₂ с МЦС Р₂ прямой.

Восстанавливаем перпендикуляр в точке S₂ к прямым.

Метод планов скоростей.

Определяем скорость точки B:

Вычисляем масштаб плана скоростей:

Выбираем на чертеже полюс p плана скоростей и изображаем скорость отрезком Рb=6.96 мм. Скорость перпендикулярна звену АB и направлена по ω₁.

Точка C принадлежит одновременно звеньям ВC и СD. Определение скорости точки C проводим по следующим векторным формулам:

(перпендикулярна CB)

(перпендикулярна CD)

На плане скоростей через точку b проводим прямую, перпендикулярную звену ВC, а из полюса р (так как точка D неподвижна) – прямую перпендикулярно СD. На пересечении этих прямых получаем точку c. На середине отрезка вc отмечаем точку S₂ и соединяем ее с полюсом р.Скорость противоположна по направлению скорости, а Скорость точки E находим по векторному уравнению:

(перпендикулярна FE)

параллельна Y-Y

Решаем графически уравнение.

Через точку F проводим прямую, перпендикулярную FE, а через полюс р - прямую, параллельную Y-Y. Точка пересечения этих прямых и будет e.

На середине ed имеем точку S₄, соединив которую с полюсом р, получим план скоростей.

Из плана скоростей имеем линейные скорости:

Угловые скорости звеньев:

Направление ω₂ определим, перенося вектор в точкуC и рассматривая вращение точки C относительно точки B. аналогично определяем направления угловых скоростей ω₄ и ω₃.

По МЦС скорость V_F=0.397м/с.

По планам скоростей скорость V_F=0.396 м/с.

Расхождение результатов:

Определение линейных ускорений точек и угловых скоростей механизма

Ускорения точек и их звеньев определяют при вычислении сил инерции:

а) графоаналитический способ:

Ускорение точки B складывается из касательного и нормального ускорений:

Согласно теореме об ускорения точек плоской фигуры:

Ускорение точки D=0. Приравниваем правые части равенств:

. (*)

Определяем нормальные ускорения:

Для определения касательных ускорений спроектируем векторное равенство (*) на оси ВХ и ВУ, взяв соответствующие значения углов с чертежа. Обозначим ,

BX:

BY:

Определяем ускорение точки C:

Определение ускорения центра масс :

Нормальное ускорение определим через угловую скорость звена 2:

Касательное ускорение определим:

,где:

проектируем векторное равенство на оси СХ и СУ.

СX:

СY:

Ускорение точки определится:

Угловое ускорение:

б) метод плана ускорений:

Определяем полное ускорение

так как

Вектор нормального ускорения направлен к центру вращения, т.е. от точкиB к A.

Точка C принадлежит одновременно звеньям ВC и СD. Рассматривая движение точки C по отношению к центрам B и D, запишем:

(перпендикулярно BC)

(перпендикулярно CD)

Вычислим нормальные составляющие:

Ускорение изобразим отрезком=мм. Тогда масштаб определиться:

Вектор направлен параллельно ВC от C к B. Вектор направлен параллельно СD от C к D. Направления тангенциальных ускорений указаны в скобках.

Теперь векторное уравнение можно решить графически. В соответствии с первым уравнением из n₁ в направлении от C к B откладываем отрезок

Через точку n₂ проводим прямую, перпендикулярную ВC (направление ). В соответствии со вторым векторным уравнением из точки(так как) параллельно СD в направлении от C к D откладываем отрезок

Через точку n₃ проводим прямую перпендикулярную СD (направление ). Отрезокизображает ускорение точкиC. Точка S₂ находится на середине отрезка вc.

Ускорение точки F определиться:

Ускорение точки E определиться:

Определим

На плане ускорений

Графически решаем записанные выше уравнения. Из точки F откладываем отрезок параллельноFE от E к F. Через точку n₄ проводим прямую, перпендикулярную FE, до пересечения с фронталью. Точку S₄ находим по методу подобия. Она лежит на середине отрезка fe.

Из плана ускорений имеем:

Угловые ускорения звеньев определим

Перенося вектор в точкуC звена 2, определим направление . Аналогично для остальных звеньев.

Расхождение результатов:

- по графическому способу

- по плану ускорений

StudFiles.ru

Что такое угловая скорость?

Что такое угловая скорость в дизайне? И как ее смотреть и почему на нее надо внимание обращать?

[ Sergio ]

Углова́я ско́рость — векторная величина, являющаяся псевдовектором (аксиальным вектором) и характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени:

Виктор поплевко

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]) . В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени.
Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью определяется формулой:

где — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = rω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения») , угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
Производная угловой скорости по времени есть угловое ускорение.
Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю) .