Приближенное значение величины и погрешности измерений

Приближенные числа и их погрешности

В самых разнообразных теоретических и прикладных исследованиях широко используются методы математического моделирования, которые сводят решение задач данной области исследования к решению адекватных (или приближенно адекватных) им математических задач. Необходимо довести решение этих задач до получения числового результата (вычисления различного рода величин, решения различных типов уравнений и т.п.). Целью вычислительной математики является разработка алгоритмов численного решения обширного круга математических задач. Методы должны быть разработаны так, чтобы их можно было эффективно реализовать с помощью современной вычислительной техники. Как правило, рассматриваемые задачи не допускают точного решения, поэтому речь идет о разработке алгоритмов, дающих приближенное решение. Для возможности замены неизвестного точного решения задачи приближенным необходимо, чтобы последнее было достаточно близко к точному. В связи с этим возникает необходимость оценки близости приближенного решения к точному и разработки приближенных методов построения приближенных решений, сколько угодно близких к точным.

Схематически вычислительный процесс заключается в том, чтобы для данной величины x (числовой, векторный и т.д.) вычислить значение некоторой функции A(x). Разность между точным и приближенным значениями величины называют погрешностью. Точное вычисление значения A(x) обычно невозможно, и вынуждает заменить функцию (операцию) A ее приближенным представлением Ã, которое можно вычислить: вычисление величины A(x), заменяется вычислением- Ã(x). Возникающую при этом погрешность A(x) - Ã(x) называют погрешностью метода. Способ оценки этой погрешности должен быть разработан вместе с разработкой метода вычисления величины Ã(x). Из возможных методов построения приближения следует использовать тот, который при имеющихся средствах и возможностях дает наименьшую погрешность.

Значение величины x, то есть исходных данных, в реальных задачах получается или непосредственно из измерений, или в результате предыдущего этапа вычислений. В этих случаях определяется лишь приближенное значение x _o величины x. Поэтому вместо величины Ã(x) может быть вычислено лишь приближенное ее значение Ã(x_o). Возникающую при этом погрешность A(x) - Ã(x_o) называют неустранимой. В результате неизбежных в ходе вычислений округлений, вместо величины Ã(x_o) вычисляется ее «округленное» значение 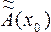, что приводит к появлению погрешности округления Ã(x_o) - 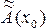. Полная погрешность вычислиниия оказывается равной A(x) - .

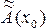Представим полную погрешность в виде

A(x) - 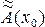= [A(x) - 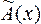] + [ 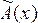- Ã(x_o)] +

+ [Ã(x_o) - 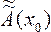] (1)

Последнее равенство показывает, что полная погрешность вычисления равна сумме погрешности метода, неустранимой погрешности и погрешности округления. Первые две составляющие погрешности можно оценить до начала вычислений. Погрешность округления оценивается лишь в ходе вычислений.

Рассмотрим следующие задачи:

а) характеристика точности приближенных чисел

б) оценка точности результата при известной точности исходных данных (оценка неустранимой погрешности)

в) определение необходимой точности исходных данных для обеспечения заданной точности результата

г) согласование точности исходных данных и вычислений с возможностями имеющихся вычислительных средств.

studopedia.ru

4 Погрешности измерений

4.1 Истинные и действительные значения физических величин. Погрешность измерения. Причины возникновения погрешностей измерений

При анализе измерений следует четко разграничивать два понятия: истинные значения физических величин и их эмпирические проявления - результаты измерений.

Истинные значения физических величин- это значения, идеальным образом отражающие свойства данного объекта как в количественном, так и в качественном отношении. Они не зависят от средств измерений и являются той абсолютной истиной, к которой стремятся при измерениях.

Напротив, результаты измерений являются продуктами познания. Представляя собой приближенные оценки значений величин, найденные в результате измерений, они зависят от метода измерений, от средств измерений и других факторов.

Погрешностью измерения называется разница между результатом измерения х и истинным значением Q измеряемой величины:

Δ= x – Q (4.1)

Но поскольку истинное значение Q измеряемой величины неизвестно, то для определения погрешности измерения в формулу (4.1) вместо истинного значения подставляют так называемое действительное значение.

Под действительным значением измеряемой величиныпонимается ее значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него.

Причинами возникновения погрешностей являются: несовершенство методов измерений, средств измерений и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений. Последние проявляются двояко. С одной стороны, все физические величины, играющие какую-либо роль при проведении измерений, в той или иной степени зависят друг от друга. Поэтому с изменением внешних условий изменяются истинные значения измеряемых величин. С другой стороны, условия проведения измерений влияют и на характеристики средств измерений и физиологические свойства органов чувств наблюдателя и через их посредство становятся источником погрешностей измерений.

4.2 Классификация погрешностей измерений в зависимости от характера их изменения

Описанные причины возникновения погрешностей являются совокупностью большого числа факторов, под влиянием которых складывается суммарная погрешность измерения. Их можно объединить в две основные группы.

К первой группе можно отнести факторы, проявляющиеся нерегулярно и неожиданно исчезающие или проявляющиеся с интенсивностью, которую трудно предвидеть. К ним относятся, например, малые флуктуации влияющих величин (температуры, давления окружающей среды и т.п.). Доля, или составляющая, суммарной погрешности измерения, возникающая под действием факторов этой группы, определяет случайную погрешность измерения.

Таким образом, случайная погрешность измерения - составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины.

При создании средств измерений и организации процесса измерения в целом интенсивность проявления факторов, определяющих случайную погрешность измерения, удается свести к общему уровню, так что все они влияют более или менее одинаково на формирование случайной погрешности. Однако некоторые из них, например, внезапное падение напряжения в сети электропитания, могут проявиться неожиданно сильно, в результате чего погрешность примет размеры, явно выходящие за границы, обусловленные ходом измерительного эксперимента. Такие погрешности в составе случайной погрешности называются грубыми. К ним тесно примыкают промахи - погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов.

Ко второй группе можно отнести факторы, постоянные или закономерно изменяющиеся в процессе измерительного эксперимента, например, плавные изменения влияющих величин. Составляющая суммарной погрешности измерения, возникающая под действием факторов этой группы, определяет систематическую погрешность измерения.

Таким образом, систематическая погрешность измерения- составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.

В процессе измерения описанные составляющие погрешности проявляются одновременно, и суммарную погрешность можно представить в виде суммы

, (4.2)

где - случайная,a Δ_s - систематическая погрешности.

Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей обработкой опытных данных. Поэтому большое значение имеет изучение погрешности как функции номера наблюдения, т.е. времени A (t). Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции:

Δ₁ = Δ(t₁), Δ₂ = Δ(t₂),..., Δ_n = Δ(t_n).

В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t_i. Можно указать лишь вероятности появления ее значений в том или ином интервале. В серии экспериментов, состоящих из ряда многократных наблюдений, мы получаем одну реализацию этой функции. При повторении серии при тех же значениях величин, характеризующих факторы второй группы, неизбежно получаем новую реализацию, отличающуюся от первой. Реализации отличаются друг от друга из-за влияния факторов первой группы, а факторы второй группы, одинаково проявляющиеся при получении каждой реализации, придают им некоторые общие черты (рисунок 4.1).

Погрешность измерений, соответствующая каждому моменту времени t_i, называется сечением случайной функции Δ(t). В каждом сечении можно найти среднее значение погрешности Δ_s(t_i), относительно которого группируются погрешности в различных реализациях. Если через полученные таким образом точки Δ_s(t_i) провести плавную кривую, то она будет характеризовать общую тенденцию изменения погрешности во времени. Нетрудно заметить, что средние значения Δ_s(tj) определяются действием факторов второй группы и представляют собой систематическую погрешность измерения в момент времени t_i, а отклонения Δ_j(t_j) от среднего значения в сечении t_i, соответствующие j-й реализации, дают значение случайной погрешности. Таким образом, имеет место равенство

(4.3)

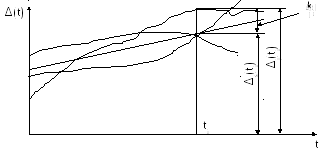
Рисунок 4.1

Предположим, что Δ_s(t_i) = 0, т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом сечении, и что все теоретико-вероятностные особенности случайных погрешностей, являющихся значениями одной реализации во всех сечениях, совпадают между собой. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины – как результаты независимых наблюдений над ней.

В таких условиях случайная погрешность измерений определяется как разность между исправленным результатом измерения Х_И (результатом, не содержащем систематическую погрешность) и истинным значением Q измеряемой величины:

Δ = X_И–Q 4.4)

причем исправленным будет результат измерений, из которого будут исключены систематические погрешности.

Подобные данные получают обычно при поверке средств измерений путем измерения заранее известных величин. При проведении же измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому неясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.

Ответ на эти вопросы можно получить, используя при обработке результатов наблюдений методы математической статистики, имеющие дело именно со случайными величинами.

4.3 Классификация погрешностей измерений в зависимости от причин их возникновения

В зависимости от причин возникновения различают следующие группы погрешностей: методические, инструментальные, внешние и субъективные.

Во многих методах измерений можно обнаружить методическую погрешность,являющуюся следствием тех или иных допущений и упрощений, применения эмпирических формул и функциональных зависимостей. В некоторых случаях влияние таких допущений оказывается незначительным, т.е. намного меньше, чем допускаемые погрешности измерений; в других случаях оно превышает эти погрешности.

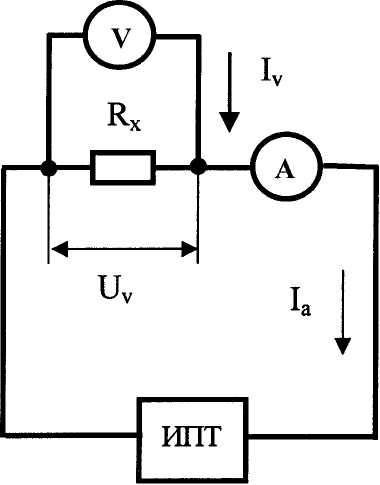
Примером методических погрешностей являются погрешности метода измерений электрического сопротивления при помощи амперметра и вольтметра (рисунок 4.2). Если сопротивление R_x определять по формуле закона Ома R_x =U_v/I_a, где U_v - падение напряжения, измеренное вольтметром V; I_а - сила тока, измеренная амперметром А, то в обоих случаях будут допущены методические погрешности измерений.

На рисунке 4.2,а сила тока I_а, измеренная амперметром, будет больше силы тока в сопротивлении R_x на значение силы тока I_v в вольтметре, включаемом параллельно сопротивлению. Сопротивление R_x, вычисленное с помощью приведенной формулы, окажется меньше действительного. На рисунке 4.2,6 напряжение, измеренное вольтметром V, окажется больше падения напряжения U_r в сопротивлении R_x на значение U_a (падение напряжения на сопротивлении амперметра А). Сопротивление, вычисленное по формуле закона Ома, окажется больше сопротивления R_x на значение R_a (сопротивление амперметра). Поправки в обоих случаях можно легко вычислить, если знать сопротивление вольтметра и амперметра. Поправки можно не вносить в том случае, если они значительно меньше допускаемой погрешности измерения сопротивления R_x, например, если в первом случае сопротивление вольтметра значительно б

б)

ольшеR_x, а во втором случае R_a значительно меньше R_x.

а)

Рисунок 4.2

Другим примером появления методической погрешности является измерение объема тел, форма которых принимается геометрически правильной, путем измерения размеров в одном или в недостаточном числе мест, например, измерение объема помещения путем измерения длины, ширины и высоты только в трех направлениях. Для точного определения объема следовало бы определить длину и ширину помещения по каждой стене, вверху и внизу, измерить высоту по углам и в середине и, наконец, углы между стенами. Этот пример иллюстрирует возможность появления существенной методической погрешности при необоснованном упрощении метода.

Как правило, методическая погрешность является систематической погрешностью.

Инструментальная погрешность— это составляющая погрешности из-за несовершенства средств измерений. Классическим примером такой погрешности является погрешность измерительного прибора, вызванная неточной градуировкой его шкалы. Очень важно четко разграничивать погрешности измерений и инструментальные погрешности. Несовершенство средств измерений является лишь одним из источников погрешности измерения и определяет только одну из ее составляющих − инструментальную погрешность. В свою очередь инструментальная погрешность является суммарной, составляющие которой − погрешности функциональных узлов − могут быть как систематическими, так и случайными.

Внешняя погрешность — составляющая погрешности измерения, вызываемая отклонением одной или нескольких влияющих величин от нормальных значений или выходом их за пределы нормальной области (например, влияние температуры, внешних электрических и магнитных полей, механических воздействий и т.п.). Как правило, внешние погрешности определяются дополнительными погрешностями применяемых средств измерений и являются систематическими. Однако при нестабильности влияющих величин они могут стать случайными.

Субъективная (личная) погрешность обусловлена индивидуальными особенностями экспериментатора и может быть как систематической, так и случайной. При применении современных цифровых средств измерений субъективной погрешностью можно пренебречь. Однако при отсчете показаний стрелочных приборов такие погрешности могут быть и значительными из-за неправильного отсчета десятых долей деления шкалы, асимметрии, возникающей при установке штриха посередине между двумя рисками, и т.п. Например, погрешности, которые делает экспериментатор при оценивании десятых долей деления шкалы прибора, могут достигать 0,1 деления. Эти погрешности проявляются в том, что для разных десятых долей деления разным экспериментаторам свойственны различные частоты оценок, причем каждый экспериментатор сохраняет присущее ему распределение в течение длительного времени. Так, один экспериментатор чаще, чем следует, относит показания к линиям, образующим края деления, и к значению 0,5 деления. Другой - к значениям 0,4 и 0,6 деления. Третий предпочитает значения 0,2 и 0,8 деления и т.д. В целом, имея в виду случайного экспериментатора, распределение погрешностей отсчитывания десятых долей деления можно считать равномерным с границами ±0,1 деления.

4.4 Формы представления погрешности измерения. Точность измерений

Погрешность измерения может быть представлена в форме абсолютной погрешности, выражаемой в единицах измеряемой величины и определяемой по формуле (4.1), или относительной погрешности, определяемой как отношение абсолютной погрешности к истинному значению измеряемой величины:

δ = Δ/Q. (4.5)

В случае выражения случайной погрешности в процентах, отношение Δ/Q умножается на 100 %. Кроме того, в формуле (4.5) допускается вместо истинного значения Q использовать результат измерения х.

Широко применяется также понятие точность измерений − характеристика, отражающая близость их результатов к истинному значению измеряемой величины. Другими словами, высокая точность соответствует малым погрешностям измерений. Поэтому количественно точность измерений можно оценить величиной, обратной модулю относительной погрешности

ε = 1/|δ|. (4.6)

StudFiles.ru

3.2. Округление

Одним из источников получения приближенных чисел является округление. Округляют как точные, так и приближенные числа.

Округлением данного числа до некоторого его разряда называют замену его новым числом, которое получается из данного путемотбрасываниявсех его цифр, записанныхправеецифры этого разряда, или путем замены его нулями. Этинули обычноподчеркивают или пишут их меньшими. Для обеспечения наибольшей близости округленного числа к округляемому следует пользоваться такимиправилами:

чтобы округлить число до единицы определенного разряда, надо отбросить все цифры, стоящие после цифры этого разряда, а в целом числе заменить их нулями. При этом учитывают следующее:

1) если первая (слева) из отбрасываемых цифрменее 5, то последнюю оставленную цифру не изменяют (округление снедостатком);

2) если первая отбрасываемая цифрабольше 5 или равна 5, то последнюю оставленную цифру увеличивают на единицу (округление сизбытком).*

Например:

Округлить:Ответы:

а) до десятых 12,34; 12,34 ≈ 12,3;

б) до сотых 3,2465; 1038,785; 3,2465 ≈ 3,25; 1038,785 ≈ 1038,79;

в) до тысячных 3,4335; 3,4335 ≈ 3,434;

г) до тысяч 12 375, 320 729. 12 375 ≈ 12000; 320 729 ≈ 321 000.

(* Несколько лет назад в случае отбрасывания одной лишь цифры 5пользовались«правилом четной цифры»: последнюю цифру оставляли без изменения, если она четная, и увеличивали на единицу, если нечетная. Теперь «правила четной цифры»непридерживаются: если отбрасывают одну цифру5, то к последней оставленной цифре добавляют единицу не зависимо от того, четная она или нечетная).

3.3. Абсолютная и относительная погрешность приближенного значения величин

Абсолютное значение разностимежду приближенным и точным (истинным) значением величины называетсяабсолютной погрешностьюприближенного значения.Например, если точное число1,214округлить до десятых, то получим приближенное число1,2. В данном случае абсолютная погрешность приближенного числа составит1,214 – 1,2 = 0,014.

Но в большинстве случаев точное значение рассматриваемой величины неизвестно, а только приближенное. Тогда и абсолютная погрешность неизвестна. В этих случаях указывают границу, которую она не превышает. Это число называютграничной абсолютной погрешностью. Говорят, что точное значение числа равно его приближенному значению с погрешностью меньшей, чем граничная погрешность.Например, число23,71есть приближенное значение числа23,7125с точностью до0,01, так как абсолютная погрешность приближения равна0,0025и меньше0,01. Здесь граничная абсолютная погрешность равна0,01.*

(* Абсолютнаяпогрешность бывает и положительной и отрицательной.Например,1,68 ≈ 1,7. Абсолютная погрешность равна1,68 – 1,7 ≈ - 0,02.Граничнаяпогрешность всегда положительна).

Граничную абсолютную погрешность приближенного числа «а» обозначают символомΔа. Запись

Х ≈ а (Δа)

следует понимать так: точное значение величины хнаходится в промежутке между числамиа+Δаи а–Δа, которые называют соответственнонижнейиверхней границейх и обозначаютНГхиВГх.

Например, еслих ≈ 2,3 (0,1),то2,2 < х< 2,4.

Наоборот, если 7,3 < х< 7,4, тох ≈ 7,35 (0,05).

Абсолютная или граничная абсолютная погрешность нехарактеризуют качество выполненного измерения. Одна и та же абсолютная погрешность может считаться значительной и незначительной в зависимости от числа, которым выражается измеряемая величина.

Например, если измеряем расстояние между двумя городами с точностью до одного километра, то такая точность вполне достаточна для этого измерения, в то же время при измерении расстояния между двумя домами одной улицы такая точность будет недопустимой.

Следовательно, точность приближенного значения величины зависит не только от величины абсолютной погрешности, но и от значения измеряемой величины. Поэтому мерой точности служит относительная погрешность.

Относительной погрешностью называется отношение абсолютной погрешности к величине приближенного числа. Отношение граничной абсолютной погрешности к приближенному числу называютграничной относительной погрешностью; обозначают её так:Δа/а. Относительную и граничную относительную погрешности принято выражатьв процентах.

Например, если измерения показали, что расстояние между двумя пунктами больше12,3 км, но меньше12,7 км, то заприближенное значение его принимаютсреднее арифметическоеэтих двух чисел, т.е. ихполусумму, тогдаграничнаяабсолютная погрешность равнаполуразностиэтих чисел. В данном случаех ≈ 12,5 (0,2).Здесь граничнаяабсолютнаяпогрешность равна0,2 км, а граничнаяотносительная:

StudFiles.ru

Абсолютная и относительная погрешности

Абсолютной погрешностью измерения называется величина, определяемая разницей между результатом измерения x и истинным значением измеряемой величины x₀:

Δx = |x – x₀|.

Величина δ, равная отношению абсолютной погрешности измерения к результату измерения, называется относительной погрешностью:

δ =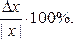

Пример 2.1. Приближённым значением числа π является 3.14. Тогда погрешность его равна 0.00159… . Абсолютную погрешность можно считать равной 0.0016, а относительную погрешность равной 0.0016 / 3.14 = 0.00051 = 0.051 %.

Значащие цифры. Если абсолютная погрешность величины a не превышает одной единицы разряда последней цифры числа a, то говорят, что у числа все знаки верные. Приближённые числа следует записывать, сохраняя только верные знаки. Если, например, абсолютная погрешность числа 52 400 равна 100, то это число должно быть записано, например, в виде 524 · 10 2 или 0.524 · 10 5. Оценить погрешность приближённого числа можно, указав, сколько верных значащих цифр оно содержит. При подсчёте значащих цифр не считаются нули с левой стороны числа.

Например, число 0.0283 имеет три верных значащих цифры, а 2.5400 – пять верных значащих цифр.

Правила округления чисел. Если приближённое число содержит лишние (или неверные) знаки, то его следует округлить. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры (d) округлённого числа. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причём если первая отбрасываемая цифра больше или равна d/2, то последняя сохраняемая цифра увеличивается на единицу.

Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются (как и лишние нули). Например, если погрешность измерения 0.001 мм, то результат 1.07005 округляется до 1.070. Если первая из изменяемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются. Например, число 148 935 с точностью измерения 50 имеет округление 148 900. Если первая из заменяемых нулями или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или идут нули, то округление производится до ближайшего чётного числа. Например, число 123.50 округляется до 124. Если первая из заменяемых нулями или отбрасываемых цифр больше 5 или равна 5, но за ней следует значащая цифра, то последняя остающаяся цифра увеличивается на единицу. Например, число 6783.6 округляется до 6784.

Пример 2.2. При округлении числа 1284 до 1300 абсолютная погрешность составляет 1300 – 1284 = 16, а при округлении до 1280 абсолютная погрешность составляет 1280 – 1284 = 4.

Пример 2.3. При округлении числа 197 до 200 абсолютная погрешность составляет 200 – 197 = 3. Относительная погрешность равна 3/197 ≈ 0.01523 или приближённо 3/200 ≈ 1.5 %.

Пример 2.4. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая – 50 г. Взвешивание дало 3600 г. Это число – приближённое. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превышает 50/3600 = 1.4 %.

Погрешности решения задачи на PC

В качестве основных источников погрешности обычно рассматривают три вида ошибок. Это так называемые ошибки усечения, ошибки округления и ошибки распространения. Например, при использовании итерационных методов поиска корней нелинейных уравнений результаты являются приближёнными в отличие от прямых методов, дающих точное решение.

Ошибки усечения

Этот вид ошибок связан с погрешностью, заложенной в самой задаче. Он может быть обусловлен неточностью определения исходных данных. Например, если в условии задачи заданы какие-либо размеры, то на практике для реальных объектов эти размеры известны всегда с некоторой точностью. То же самое касается любых других физических параметров. Сюда же можно отнести неточность расчётных формул и входящих в них числовых коэффициентов.

Ошибки распространения

Данный вид ошибок связан с применением того или иного способа решения задачи. В ходе вычислений неизбежно происходит накопление или, иначе говоря, распространение ошибки. Помимо того, что сами исходные данные не являются точными, новая погрешность возникает при их перемножении, сложении и т. п. Накопление ошибки зависит от характера и количества арифметических действий, используемых в расчёте.

Ошибки округления

Это тип ошибок связан с тем, что истинное значение числа не всегда точно сохраняется компьютером. При сохранении вещественного числа в памяти компьютера оно записывается в виде мантиссы и порядка примерно так же, как отображается число на калькуляторе.

studopedia.ru