схема это:
схема схе́ма сущ., ж., употр. сравн. часто Морфология: (нет) чего? схе́мы, чему? схе́ме, (вижу) что? схе́му, чем? схе́мой, о чём? о схе́ме; мн. что? схе́мы, (нет) чего? схе́м, чему? схе́мам, (вижу) что? схе́мы, чем? схе́мами, о чём? о схе́мах 1. Схемой называется взаимосвязь, взаимодействие между частями какого-либо устройства, прибора.Сложная электронная схема.
2. Схемой называется чертёж, который показывает и объясняет принцип работы какого-либо устройства.Читать, чертить схемы. | Схема телефонного аппарата. | Описание автомобиля снабжено схемами. | Собрать по схеме модель самолёта.
3. Схемой называют графическое изображение взаимного пространственного расположения чего-либо.Схема линий метрополитена. | Схема коммуникаций аэропорта.
4. Схемой называют план действий, продуманный порядок выполнения чего-либо.На все случаи жизни готовых схем нет. | Основная схема выполнения задания чётко разделяется на три части. | При покупке квартиры по безналичному расчёту схема оплаты упрощается.
5. Схемой называют изложение, описание чего-либо в самых общих, основных чертах, без деталей, подробностей.Вместо полнокровного романа вышла сухая схема событий.
• схемати́чный прил. • схемати́ческий прил. • схемати́чески нар. • схемати́чно нар. • схематизи́ровать глаг., нсв., св.Толковый словарь русского языка Дмитриева. Д. В. Дмитриев. 2003.
.
dic.academic.ru
3.1.2 Соединение в треугольник. Схема, определения
Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке.
На рис. 5 изображена трехфазная цепь, соединенная треугольником. Как видно из рис. 5, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы Uл = Uф
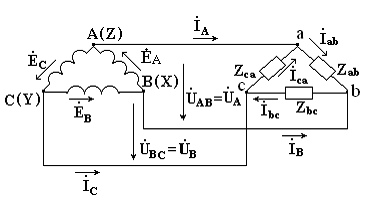
Рис. 5. Трехфазная цепь, соединенная треугольником
Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с:
![]()
или

Следовательно, при симметричной нагрузке Iл = √3 Iф
Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме "звезда".
3.2 Расчёт симметричных режимов работы трёхфазных цепей
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в комплексной форме в полной мере распространяются на них.
Трёхфазный приемник и вообще трёхфазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. ZA = ZB = ZC. В противном случае они являются несимметричными. Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 6 является симметричным, а на рис. 7 – нет.
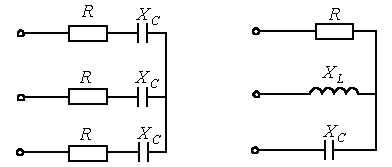
Рис. 6. Рис. 7.
Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол ![]() . Вследствие указанного расчет таких цепей проводится для одной фазы, в качестве которой обычно принимают фазуА. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы А фазового сдвига
. Вследствие указанного расчет таких цепей проводится для одной фазы, в качестве которой обычно принимают фазуА. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы А фазового сдвига ![]() при сохранении неизменным ее модуля. Так для симметричного режима работы цепи на рис. 8
при сохранении неизменным ее модуля. Так для симметричного режима работы цепи на рис. 8

Рис. 8.
при известных линейном напряжении и сопротивлениях фаз ZAB = ZBC = ZCA = Z можно записать
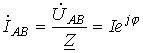
где угол фазового сдвига φ между напряжением и током определяется характером нагрузки Z.
Тогда на основании вышесказанного токи в других двух фазах равны:
![]()
![]()
Комплексы линейных токов можно найти с использованием векторной диаграммы, из которой следует
![]()
![]()
![]()
Пример расчёта симметричного режима работы трёхфазной цепи приведён в приложении 3.
4. Электрические цепи периодического несинусоидального тока
Периодические несинусоидальные токи и напряжения в электрических цепях возникают в случае действия в них несинусоидальных ЭДС или наличия в них нелинейных элементов. Реальные ЭДС, напряжения и токи в электрических цепях синусоидального переменного тока по разным причинам отличаются от синусоиды. В энергетике появление несинусоидальных токов или напряжений нежелательно, т.к. вызывает дополнительные потери энергии. Однако существуют большие области техники (радиотехника, автоматика, вычислительная техника, полупроводниковая преобразовательная техника), где несинусоидальные величины являются основной формой ЭДС, токов и напряжений.
Рассмотрим краткие теоретические сведения и методику расчёта линейных электрических цепей при воздействии на них источников периодических несинусоидальных ЭДС.
4.1.Разложение периодической функции в тригонометрический ряд
Как известно, всякая периодическая функция, имеющая конечное число разрывов первого рода и конечное число максимумов и минимумов за период,
может быть разложена в тригонометрический ряд (ряд Фурье):
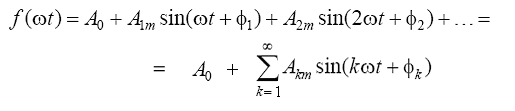
Первый член ряда называется постоянной составляющей, второй член – основной или первой гармоникой. Остальные члены ряда называются высшими гармониками.
Если в выражении раскрыть синусы суммы каждой из гармоник, то оно примет вид :
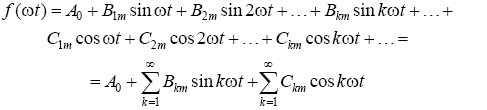
где
![]()
В случае аналитического задания функции f(ωt) коэффициенты ряда могут быть вычислены с помощью следующих выражений:
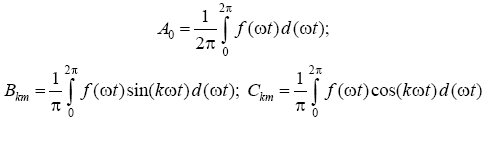
После чего производится расчёт амплитуд и начальных фаз гармонических составляющих ряда:

Коэффициенты ряда Фурье большей части периодических функций, встречающихся в технике, приводятся в справочных данных или в учебниках по электротехнике.
StudFiles.ru
Разностная схема
Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например краевые условия и/или начальное распределение). Таким образом, разностные схемы применяются для сведения дифференциальной задачи, имеющей континуальный характер, к конечной системе уравнений, численное решение которых принципиально возможно на вычислительных машинах. Алгебраические уравнения, поставленные в соответствие дифференциальному уравнению получаются применением разностного метода, что отличает теорию разностных схем от других численных методов решения дифференциальных задач (например проекционных методов, таких как метод Галёркина).
Решение разностной схемы называется приближенным решением дифференциальной задачи.
Хотя формальное определение не накладывает существенных ограничений на вид алгебраических уравнений, но на практике имеет смысл рассматривать только те схемы, которые каким-либо образом отвечают дифференциальной задаче. Важными понятиями теории разностных схем являются понятия сходимости, аппроксимации, устойчивости, консервативности.
Аппроксимация
Говорят, что дифференциальный оператор L ( u ) {\displaystyle L(u)} , определённый на функциях u {\displaystyle u} , заданных в области D ⊂ R N {\displaystyle D\subset \mathbb {R} ^{N}} , аппроксимируется на некотором классе функций u ∈ U {\displaystyle u\in U} конечно-разностным оператором R h ( u h ) {\displaystyle R_{h}(u_{h})} , определённым на функциях u h {\displaystyle u_{h}} , заданных на сетке, зависящей от шага h {\displaystyle h} , если выполняется условие сходимости
| | L ( u ) − R h ( u h ) | | → 0 , h → 0 ( ∀ u ∈ U ) . {\displaystyle ||L(u)-R_{h}(u_{h})||\to 0,\ \ h\to 0\ \ \ (\forall u\in U).}Говорят, что аппроксимация имеет порядок точности k {\displaystyle k} , если
| | L ( u ) − R h ( u h ) | | ≤ h k M , h → 0 ( ∀ u ∈ U ) , {\displaystyle ||L(u)-R_{h}(u_{h})||\leq h^{k}M,\ \ h\to 0\ \ \ (\forall u\in U),}где M {\displaystyle M} — константа, зависящая от конкретной функции u ∈ U {\displaystyle u\in U} , но не зависящая от шага h {\displaystyle h} . Норма, использованная выше, может быть различной, и понятие аппроксимации зависит от её выбора. Часто используется дискретный аналог нормы равномерной непрерывности:
| | u h | | = max n | u h ( x n ) | , {\displaystyle ||u_{h}||=\max _{n}|u_{h}(x_{n})|,}иногда используются дискретные аналоги интегральных норм[1][2].
Пример. Аппроксимация оператора L ( u ) = u x x {\displaystyle L(u)=u_{xx}} конечно-разностным оператором
R h ( u h ) ( x n ) = u n + 1 − 2 u n + u n − 1 h 2 , u i = u ( x i ) , x i + 1 = x i + h , {\displaystyle R_{h}(u_{h})(x_{n})={\frac {u_{n+1}-2u_{n}+u_{n-1}}{h^{2}}},\quad u_{i}=u(x_{i}),\quad x_{i+1}=x_{i}+h,}на ограниченном интервале D ⊂ R {\displaystyle D\subset \mathbb {R} } имеет второй порядок точности на классе гладких функций U = C 4 ( D ) {\displaystyle U=C^{4}(D)} .
ДоказательствоС помощью формулы Тейлора
u n ± 1 = u n ± h u x ( x n ) + h 2 2 u x x ( x n ) ± h 3 3 ! u x x x ( x n ) + h 4 4 ! u x x x x ( x n + ξ ± ) , ξ ± ∈ ( 0 , ± h ) , {\displaystyle u_{n\pm 1}=u_{n}\pm hu_{x}(x_{n})+{\frac {h^{2}}{2}}u_{xx}(x_{n})\pm {\frac {h^{3}}{3!}}u_{xxx}(x_{n})+{\frac {h^{4}}{4!}}u_{xxxx}(x_{n}+\xi _{\pm }),\quad \xi _{\pm }\in (0,\pm h),}получается оценка:
| u x x ( x n ) − R h ( u h ) ( x n ) | = 1 h 2 | u n + 1 − 2 u n + u n − 1 − h 2 u x x ( x n ) | = h 2 4 ! | u x x x x ( x n + ξ + ) + u x x x x ( x n + ξ − ) | ≤ h 2 4 ! C , {\displaystyle \bigl u_{xx}(x_{n})-R_{h}(u_{h})(x_{n})\bigr ={\frac {1}{h^{2}}}\,\bigl u_{n+1}-2u_{n}+u_{n-1}-h^{2}u_{xx}(x_{n})\bigr ={\frac {h^{2}}{4!}}\,\Bigl u_{xxxx}(x_{n}+\xi _{+})+u_{xxxx}(x_{n}+\xi _{-})\Bigr \leq {\frac {h^{2}}{4!}}\,C,}где константа
C = 2 sup x ∈ D | u x x x x ( x ) | ∞ . {\displaystyle C=2\sup \limits _{x\in D}|u_{xxxx}(x)| , если и само дифференциальное уравнение, и граничные (и начальные) условия аппроксимируются соответствующими конечно-разностными операторами с порядком точности не ниже k {\displaystyle k} .Пример. Аппроксимация уравнения теплопроводности u t − u x x = 0 {\displaystyle u_{t}-u_{xx}=0} (разностная схема в частных производных) конечно-разностным уравнением R h ( u h ) = 0 {\displaystyle R_{h}(u_{h})=0} , где
R h ( u h ) ( t m , x n ) = u n m + 1 − u n m Δ t − u n + 1 m − 2 u n m + u n − 1 m h 2 , {\displaystyle R_{h}(u_{h})(t_{m},x_{n})={\frac {u_{n}^{m+1}-u_{n}^{m}}{\Delta t}}-{\frac {u_{n+1}^{m}-2u_{n}^{m}+u_{n-1}^{m}}{h^{2}}},} u j i = u ( t i , x j ) , t i + 1 = t i + Δ t , x j + 1 = x j + h , Δ t = σ h 2 , σ = c o n s t > 0 , {\displaystyle u_{j}^{i}=u(t_{i},x_{j}),\quad t_{i+1}=t_{i}+\Delta t,\quad x_{j+1}=x_{j}+h,\quad \Delta t=\sigma h^{2},\quad \sigma =const>0,}имеет второй порядок точности по координате и первый порядок точности по времени на классе C 4 {\displaystyle C^{4}} -гладких функций.
Устойчивость
Условия аппроксимации недостаточно для того, чтобы результат разностной схемы приближался к точному ответу при h→0. В случае схем, коэффициенты которых не зависят от решения дифференциального уравнения, нужно выполнение условия устойчивости. Такие схемы можно представить как некоторый линейный оператор, который преобразует значения функции в момент t в значения функции в момент t+h. Условие устойчивости требует, чтобы собственные числа (вообще говоря комплексные) этого оператора не превосходили по модулю 1+ch, где с — некоторая константа, при h→0. Если это условие не выполнено, то погрешности схемы быстро возрастают и результат тем хуже, чем меньше шаг. Если выполнены как условие аппроксимации, так и условие устойчивости, то результат разностной схемы сходится к решению дифференциального уравнения (теорема Филиппова-Рябенького).[1][3]
Условие Куранта
Условие Куранта (в англоязычной литературе англ. Courant–Friedrichs–Lewy condition, CFL) — скорость распространения возмущений в разностной задаче не должна быть меньше, чем в дифференциальной. Если это условие не выполнено, то результат разностной схемы может не стремиться к решению дифференциального уравнения. Другими словами, за один шаг по времени частица не должна «пробегать» более одной ячейки.
В случае схем, коэффициенты которых не зависят от решения дифференциального уравнения, условие Куранта следует из устойчивости.
Для гиперболических систем уравнений это условие часто имеет вид
τ ≤ min ( h | λ | m a x ) {\displaystyle \tau \leq \min \left({\frac {h}{|\lambda |_{max}}}\right)}
( τ {\displaystyle \tau } — шаг по времени, h {\displaystyle h} — шаг пространственной сетки, | λ | m a x {\displaystyle |\lambda |_{max}} — максимальное по модулю собственное значение в точке. Минимум берется по всем точкам сетки.)
Классификация схем
Явные схемы
Явные схемы вычисляют значение результата через несколько соседних точек данных. Пример явной схемы для дифференцирования: f ′ ( x ) = f ( x + h ) − f ( x − h ) 2 h {\displaystyle f'(x)={\frac {f(x+h)-f(x-h)}{2h}}} (2-й порядок аппроксимации). Явные схемы часто оказываются неустойчивыми.
Согласно теореме Годунова среди линейных разностных схем для уравнения переноса с порядком аппроксимации выше первого нет монотонных.
Неявные схемы
Неявные схемы используют уравнения, которые выражают данные через несколько соседних точек результата. Для нахождения результата решается система линейных уравнений. Пример неявной схемы для уравнения струны: f ( x , t + h ) − 2 f ( x , t ) + f ( x , t − h ) = f ( x + h , t + h ) − 2 f ( x , t + h ) + f ( x − h , t + h ) {\displaystyle f(x,t+h)-2f(x,t)+f(x,t-h)=f(x+h,t+h)-2f(x,t+h)+f(x-h,t+h)} . Неявные схемы обычно являются устойчивыми.
Полунеявные схемы
На одних шагах применяется явная схема, на других — неявная (как правило, эти шаги чередуются).
Пример — Схема Кранка-Никольсо́н, когда решение берется в виде среднего от явной и неявной схемы решения для повышения точности
Компактные схемы
Компактные схемы используют уравнения, которые связывают значения результата в нескольких соседних точках с значениями данных в нескольких соседних точках. Это позволяет повысить порядок аппроксимации. Пример компактной схемы для дифференцирования: 1 6 f ′ ( x − h ) + 2 3 f ′ ( x ) + 1 6 f ′ ( x + h ) = f ( x + h ) − f ( x − h ) 2 h {\displaystyle {\frac {1}{6}}f'(x-h)+{\frac {2}{3}}f'(x)+{\frac {1}{6}}f'(x+h)={\frac {f(x+h)-f(x-h)}{2h}}} (4-тый порядок аппроксимации).
Консервативные схемы
Когда разностная схема удовлетворяет тем же интегральным соотношениям (например, сохранению энергии, энтропии), что и первоначальное дифференциальное уравнение, то говорят о свойстве консервативности. Консервативные схемы обычно представляются в дивергентном виде.
Примеры консервативных схем гидродинамики — схема Самарского, метод крупных частиц Белоцерковского.
Схемы на смещенных сетках
В этих схемах сетки, на которых задан результат, и данные смещены относительно друг друга. Например, точки результата находятся посередине между точками данных. В некоторых случаях это позволяет использовать более простые граничные условия.
Ссылки
- «Разностные схемы» — Глава в wikibooks на тему «Разностные схемы для гиперболических уравнений»
- Демьянов А. Ю., Чижиков Д. В. Неявная гибридная монотонная разностная схема второго порядка точности
- Рябенький В. С., Филиппов А. Ф. Об устойчивости разностных уравнений. — М.: Гостехиздат, 1956.
- Годунов С. К., Рябенький В. С. Введение в теорию разностных схем. — М.: Физматгиз, 1962.
- Бабенко К. И. Основы численного анализа. — М.: Наука, 1986.
- Березин И. С., Жидков Н. П. Методы вычислений, — Любое издание.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы, — Любое издание.
- Марчук Г. И. Методы вычислительной математики. — М.: Наука, 1977.
ru.wikipedia.org
Цикл развития папоротника: схема, определение, таблица и описание
Папоротники поистине являются одними из самых загадочных представителей растительного мира. С ними связаны красивые истории и легенды. В нашей статье мы рассмотрим цикл развития папоротника, схему жизненного периода и особенности этих растений.
Характерные черты отдела
Представители папоротниковидных представлены двумя жизненными формами. В лесах умеренного климатического пояса растут многолетние травы. Их надземная часть состоит только из листьев. А сам побег видоизменен в корневище и расположен под землей. От него отходят пучки мочковатой корневой системы. В зоне влажных тропических лесов встречаются древовидные папоротники. Их стебель может быть вьющимся или прямостоячим. В любом случае у этих видов он достигает нескольких десятков метров.
Папоротники относятся к группе высших споровых растений, представители которой являются первыми выходцами на сушу. В процессе эволюции у них сформировались настоящие ткани и органы. Именно это позволило освоить этим растениям новую среду обитания. Название данной систематической группы также связано с тем, что папоротники формируют споры, которые являются клетками бесполого размножения.

Цикл развития папоротника: схема описания
Для всех папоротников характерно наличие жизненного цикла. Так называется период между двумя одинаковыми этапами развития поколений. Типичным для этих растений является цикл развития папоротника орляка. Его можно представить в виде этапов, представленных в таблице.
| Период жизненного цикла | Функция |
| Растение бесполого поколения | Фотосинтез, формирование спор, вегетативное размножение, минеральное питание, транспирация, закрепление растения в почве |
| Споры | Бесполое размножение, формирование гаметофита |
| Заросток | Фотосинтез, закрепление растения в почве, формирование половых клеток - яйцеклеток и сперматозоидов |
| Гаметы | Половое размножение растения |
| Зародыш | Формирование бесполого поколения - спорофита |
Далее цикл развития папоротника повторяется. Этот процесс обеспечивает непрерывность существования всех отделов высших споровых растений. А теперь рассмотрим каждый этап более подробно.
Растение бесполого поколения
Знакомство с циклом развития папоротника, схема которого представлена ниже, мы начнем со спорофита. Именно так называется взрослое листостебельное растение, которое образует значительные заросли в лесах умеренного пояса. На поверхности мы можем видеть только листья папоротника. Они бывают двух видов. Молодые листья спирально закручены, их называют вайи. Они нарастают своей верхушкой и достигают значительных размеров. Так появляются пышные и раскидистые листья взрослых растений.
Спорофит является преобладающим поколением этих растений. Это является значительным отличием в циклах развития мхов и папоротников. У первых основным поколением является гаметофит. Он имеет вид зеленого листостебельного ковра и размножается с помощью половых клеток.

Где расположены спорангии
Следующим этапом цикла развития папоротника является созревание органов бесполого размножения. Они называются спорангиями. Эти структуры имеют вид небольших коричневых бугорков, расположенных на нижней стороне листьев. Сверху они дополнительно защищены пленчатыми "покрывальцами". Спорангии папоротников собраны в группы, которые называются сорусами.
В конце лета эти структуры темнеют. Это значит, что спорангии созрели. Далее они раскрываются, и в землю высыпаются тысячи мелких клеток. Это и есть споры. При наличии достаточного количества влаги они сразу начинают прорастать.

Что такое заросток
Результатом развития спор является заросток. Это и есть особь полового поколения, которая является следующим звеном в цикле развития папоротника. Долгое время ученые даже не знали о его существовании. Все дело в том, что заросток имеет очень мелкие размеры - всего до сантиметра в диаметре. Внешне он представляет собой пластину зеленого цвета сердцевидной формы. Заросток развивается на почве, к которой прикрепляется с помощью ризоидов.
По мере развития гаметофита на его нижней стороне формируются органы полового размножения. В них созревают половые клетки двух видов: яйцеклетки и сперматозоиды.
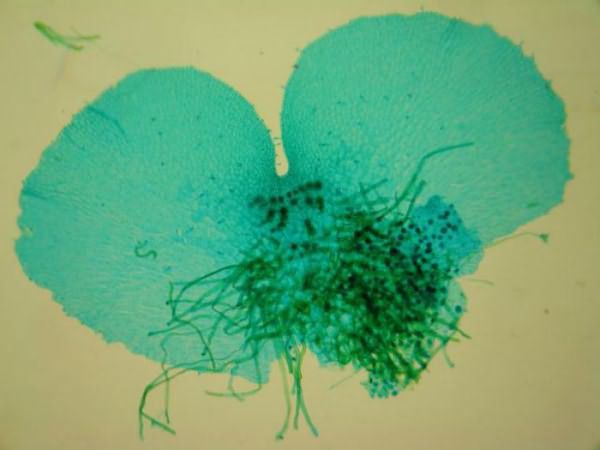
Условия оплодотворения в цикле развития папоротника орляка
Гаплоидный набор хромосом, который имеют половые клетки гаметофита, изменяется на двойной в процессе их слияния. Оплодотворение у папоротников имеет свои особенности. Во-первых, мужские и женские половые клетки на одном заростке созревают в разное время. Поэтому слияние гамет возможно только между разными растениями. Такой тип оплодотворения называется перекрестным.
Второй особенностью этого процесса у папоротников является обязательное наличие воды. Дело в том, что половые клетки споровых растений не могут самостоятельно двигаться. Поэтому сперматозоид может добраться до яйцеклетки только с помощью воды. Таким образом, папоротники хоть и относятся к группе первых наземных растений, но не утратили связь с прежней средой обитания.
Далее из оплодотворенной яйцеклетки развивается растение бесполого поколения, на нем созревают споры, и процесс повторяется.

Продолжительность жизни
Сколько может повторяться цикл развития папоротника? Это зависит от конкретного вида растения и места его произрастания. Так, у травянистых форм умеренных широт листья отмирают каждый сезон, а в тропиках растут несколько лет. Но благодаря наличию подземного видоизменения побега, который называется корневищем, само растение остается жизнеспособным независимо от времени года и климатических условий. Во многом именно эта особенность строения сохранила эти древние растения до современного этапа развития органического мира.
Корни папоротников выполняют свои функции в среднем около четырех лет, после чего заменяются новыми. А вот побег может сохранять свою жизнеспособность до 100 лет.

Итак, мы рассмотрели особенности развития одного из отделов высших споровых растений - Папоротниковидные. Для этих растений характерны следующие признаки:
- Появление настоящих тканей (механических, проводящих, покровных) и вегетативных органов (листьев, придаточных корней, видоизмененного подземного побега).
- Бесполое размножение осуществляется с помощью специализированных клеток - спор.
- В цикле развития папоротника преобладает спорофит. Это бесполое поколение, имеющее листостебельное строение.
- Гаметофит папоротника называется заростком. Он представляет собой зеленую пластинку сердцевидной формы с диаметром до 1 см. Заросток развивается отдельно от спорофита и анатомически с ним не связан.
- В жизненном цикле наблюдается последовательное чередование поколений - полового и бесполого.
fb.ru
*Внешняя схема а Отображение "внешний/концептуальный" схемы Определение структур хранения (внутренняя схема)
Схемы и отображения создаются и сопровождаются администратором Л базы данных (АБД) *
![]()
Базовый язык +
подъязык данных!
Базовый язык +
подъязык данных!
Базовый язык +^Внешняя схема Б
кюдъяэык данных!Отображение "внешний/концептуальный" схемы А
Концептуальное представление
Отображение "концептуальный/внутренний"
\
Внешнее представление А
Концептуальная схема
^ ^^ ~^ ^ ^ ^
Хранимая база данных (внутреннее представление)
L_J L_J L_J L_J L_J I )
j *Интерфейс пользователя |
Рис. 2.3. Детальная схема архитектуры системы баз данных
Замечание. Из соображений точности следует отметить, что современный язык PL/I на самом деле вообще не включает никаких особых средств для работы с базами данных. Оператор "языка обработки данных" (оператор CALL), в частности, обычно просто обра- щается к СУБД (хотя такие обращения могут быть синтаксически скрыты, чтобы сделать их более дружественными по отношению к пользователю). Разговор о внедрении опера- торов языка SQL будет продолжен в главе 4.
Вернемся к архитектуре. Как уже отмечалось, отдельного пользователя интересу- ет лишь некоторая часть всей базы данных. Кроме того, представление пользователя об этой части будет, безусловно, чем-то абстрактным по сравнению с выбранным способом физического хранения данных. В соответствии с терминологией ANSI/SPARC представление отдельного пользователя называется внешним пред- ставлением. Таким образом, внешнее представление — это содержимое базы дан- ных, каким его видит определенный пользователь (т.е. для каждого пользователя внешнее представление и есть та база данных, с которой он работает). Например, пользователь из отдела кадров может рассматривать базу данных как набор записей с информацией об отделах плюс набор записей с информацией о служащих и ничего не знать о записях с информацией о материалах и их поставщиках, с которыми рабо- тают пользователи в отделе снабжения.
В общем случае внешнее представление состоит из некоторого множества экземп- ляров каждого из многих типов внешних записей (которые вовсе не обязательно должны совпадать с хранимыми записями)2. Предоставляемый в распоряжение поль- зователя подъязык данных всегда определяется в терминах внешних записей. Напри- мер, операция выборки языка обработки данных осуществляет выборку экземпляров внешних, а не хранимых записей.
Замечание. Теперь мы видим, что термин "логическая запись", употреблявшийся в главе 1, на самом деле относится к внешним записям. Поэтому в дальнейшем мы бу- дем избегать его использования.
2В данном случае предполагается, что вся информация на внешнем уровне представлена в форме записей. Но некоторые системы позволяют представлять информацию иначе: либо вме- сто записей, либо совместно с ними. Для использующих такие альтернативные методы систем все определения и пояснения этого раздела требуют соответствующих изменений. Это замеча- ние касается также концептуального и внутреннего уровней. Детальное обсуждение подобных вопросов в этой части книги было бы преждевременным, поэтому мы вернемся к ним позднее, в главах 13 (в особенности — в разделе "Список литературы ") и 24.
Каждое внешнее представление определяется посредством внешней схемы, которая, в основном, состоит из определений записей каждого из типов, присутст- вующих в этом внешнем представлении (см. рис. 2.2). Внешняя схема записывает- ся с помощью языка определения данных, являющегося подмножеством подъязы- ка данных пользователя. (Поэтому язык определения данных иногда называют внешним языком определения данных.) Например, тип внешней записи о работни- ке можно определить как шестисимвольное поле с номером работника, плюс поле из пяти десятичных цифр, предназначенное для его зарплаты, и т.д. Кроме того, может потребоваться определить отображение между внешней и исходной кон- цептуальной схемами (подробности — в следующем разделе). Это отображение рассматривается в разделе 2.6.StudFiles.ru
Читайте также
![Акт определение Акт определение]() Акт определение
Акт определение![Двигатель определение Двигатель определение]() Двигатель определение
Двигатель определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Определение цены деления шприца Определение цены деления шприца]() Определение цены деления шприца
Определение цены деления шприца![Определение высоты объекта Определение высоты объекта]() Определение высоты объекта
Определение высоты объекта![Определение ph воды Определение ph воды]() Определение ph воды
Определение ph воды![Легальное определение юридического лица дано Легальное определение юридического лица дано]() Легальное определение юридического лица дано
Легальное определение юридического лица дано![Деталь определение Деталь определение]() Деталь определение
Деталь определение![Закон джоуля ленца формула и определение Закон джоуля ленца формула и определение]() Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение![Машина определение Машина определение]() Машина определение
Машина определение![Места массового скопления людей определение Места массового скопления людей определение]() Места массового скопления людей определение
Места массового скопления людей определение![Определение надежности Определение надежности]() Определение надежности
Определение надежности
 Акт определение
Акт определение Двигатель определение
Двигатель определение Болезнь определение
Болезнь определение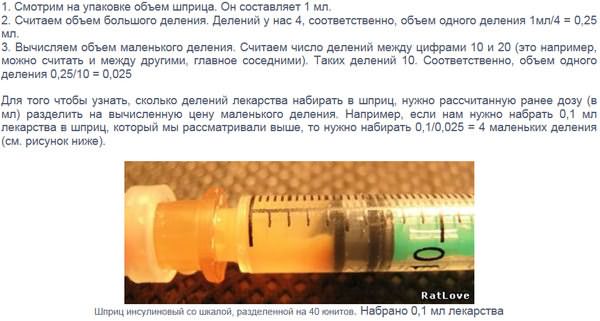 Определение цены деления шприца
Определение цены деления шприца Определение высоты объекта
Определение высоты объекта Определение ph воды
Определение ph воды Легальное определение юридического лица дано
Легальное определение юридического лица дано Деталь определение
Деталь определение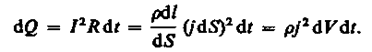 Закон джоуля ленца формула и определение
Закон джоуля ленца формула и определение Машина определение
Машина определение Места массового скопления людей определение
Места массового скопления людей определение Определение надежности
Определение надежности