Интегральная теорема Лапласа
Вновь предположим, что производится писпытаний, в каждом из которых вероятность появления события Апостоянна и равна р(0рРп (k1 , k2)того, что событие А появится в писпытаниях не менее k1и не более k2раз (для краткости будем говорить «от k1до k2раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже, опустив доказательство.
Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рп (k1 , k2) того, что событие А появится в п испытаниях от k1 до k2 раз, приближенно равна определенному интегралу
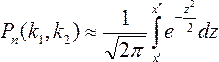 (*)
(*)
где 
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл 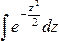 не выражается через элементарные функции.
не выражается через элементарные функции.
Таблица для интеграла 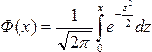 приведена в приложении 2.
приведена в приложении 2.
В таблице даны значения функции Ф(х) для положительных значений хи для х = 0; для х.
В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5. Функцию Ф (х) часто называют функцией Лапласа.
Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (*) так:
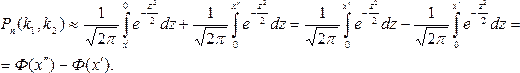
Итак, вероятность того, что событие А появится в п независимых испытаниях от k1 до k2 раз, вычисляется по формуле:
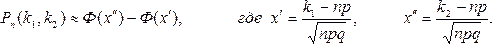
Пример 4. Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. По условию, р=0,2; q=0,8; n=400; k1=70; k2=100. Воспользуемся интегральной теоремой Лапласа:
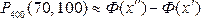
Вычислим нижний и верхний пределы интегрирования:
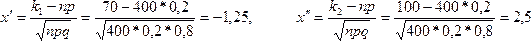
Таким образом, имеем
Р400(70, 100) = Ф(2,5) – Ф(–1,25) = Ф(2,5) + Ф(1,25).
По таблице приложения 2 находим:
Ф (2,5) = 0,4938; Ф (1,25)=0,3944.
Искомая вероятность равна:
Р400 (70, 100) = 0,4938 + 0,3944 = 0,8882.
Задачи
1. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент:
а) включено 4 мотора; б) включены все моторы; в) выключены все моторы.
Отв. а) Р6(4)=0,246; б) Р6(6)=0,26; в) Р6(0) = 0,000064.
2. Найти вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна 0,3.
Отв. Р = 1 – [Р5(0) + Р5(1)] = 0,472.
3. Событие В появится в случае, если событие А появится не менее двух раз. Найти вероятность того, что наступит событие В, если будет произведено 6 независимых испытаний, в каждом из которых вероятность появления события А равна 0,4.
Отв. Р = 1 – [Р6(0) + Р6(1)] = 0,767.
4. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза.
Отв. Р = 1 – [Р8(0) + Р8(1)] = 0,19.
5. Монету бросают 6 раз. Найти вероятность того, что герб выпадет:
а) менее двух раз; б) не менее двух раз.
Отв. а) Р = Р6(0) + Р6(1) = 7/64; б)Q = l – [Р6(0) + Р6(1)]=57/64.
6. Вероятность попадания в цель при одном выстреле из орудия р=0,9. Вероятность поражения цели при k попаданиях (k≥1) равна 1-qk. Найти вероятность того, что цель будет поражена, если сделано два выстрела.
Указание. Воспользоваться формулами Бернулли и полной вероятности.
Отв. 0,9639.
7. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Отв. Р400 (104) = 0,0006.
8. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена:
а) не менее 70 и не более 80 раз; б) не более 70 раз.
Отв. а) Р100(70,80) = 2Ф(1,15) = 0,7498;
б) Р100(0; 70)= – Ф (1,15) + 0,5 = 0,1251.
ПРИЛОЖЕНИЕ 1. Таблица значений локальной функции Лапласа 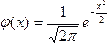
| 0,0 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3726 | 0,3712 | 0,3698 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,4 | 0,3683 | 0,3668 | 0,3652 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,5 | 0,3521 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,9 | 0,2661 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,0 | 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,2012 | 0,1989 | 0,1965 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,2 | 0,1942 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,5 | 0,1295 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,8 | 0,0790 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,0 | 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0395 | 0,0387 | 0,0379 | 0,0371 | 0,0363 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,2 | 0,0353 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0046 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,0 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0021 | 0,0020 | 0,0019 | 0,0018 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,3 | 0,0017 | 0,0016 | 0,0015 | 0,0014 | 0,0013 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,4 | 0,0012 | 0,0012 | 0,0011 | 0,0010 | 0,0010 | 0,0009 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0006 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,6 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0004 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ПРИЛОЖЕНИЕ 2. Таблица значений интегральной функции Лапласа 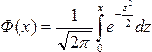
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[1] Функцию φ(х) называют асимптотическим приближением функции f(x), если
studopedia.ru
/ таблица значений функции Лапласа
Сайт www.MatBuro.ru
©МатБюро - Решение задач по высшей математике, теории вероятностей
|
Функция Лапласа |
y =Φ(x)= |
1 |
∫x |
e−t2 / 2dt |
|||||||
|
2π |
|||||||||||
|
0 |
|||||||||||
|
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
||||
|
0 |
0 |
||||||||||
|
0,01 |
0,004 |
0,13 |
0,0517 |
0,25 |
0,0987 |
0,37 |
0,1443 |
||||
|
0,02 |
0,008 |
0,14 |
0,0557 |
0,26 |
0,1026 |
0,38 |
0,148 |
||||
|
0,03 |
0,012 |
0,15 |
0,0596 |
0,27 |
0,1064 |
0,39 |
0,1517 |
||||
|
0,04 |
0,016 |
0,16 |
0,0636 |
0,28 |
0,1103 |
0,4 |
0,1554 |
||||
|
0,05 |
0,0199 |
0,17 |
0,0675 |
0,29 |
0,1141 |
0,41 |
0,1591 |
||||
|
0,06 |
0,0239 |
0,18 |
0,0714 |
0,3 |
0,1179 |
0,42 |
0,1628 |
||||
|
0,07 |
0,0279 |
0,19 |
0,0753 |
0,31 |
0,1217 |
0,43 |
0,1664 |
||||
|
0,08 |
0,0319 |
0,2 |
0,0793 |
0,32 |
0,1255 |
0,44 |
0,17 |
||||
|
0,09 |
0,0359 |
0,21 |
0,0832 |
0,33 |
0,1293 |
0,45 |
0,1736 |
||||
|
0,1 |
0,0398 |
0,22 |
0,0871 |
0,34 |
0,1331 |
0,46 |
0,1772 |
||||
|
0,11 |
0,0438 |
0,23 |
0,091 |
0,35 |
0,1368 |
0,47 |
0,1808 |
||||
|
0,12 |
0,0478 |
0,24 |
0,0948 |
0,36 |
0,1406 |
0,48 |
0,1844 |
||||
|
0,49 |
0,1879 |
1,02 |
0,3461 |
1,55 |
0,4394 |
2,16 |
0,4846 |
||||
|
0,5 |
0,1915 |
1,03 |
0,3485 |
1,56 |
0,4406 |
2,18 |
4854 |
||||
|
0,51 |
0,195 |
1,04 |
0,3508 |
1,57 |
0,4418 |
2,2 |
0,4861 |
||||
|
0,52 |
0,1985 |
1,05 |
0,3531 |
1,58 |
0,4429 |
2,22 |
0,4868 |
||||
|
0,53 |
0,2019 |
1,06 |
0,3554 |
1,59 |
0,4441 |
2,24 |
0,4875 |
||||
|
0,54 |
0,2054 |
1,07 |
0,3577 |
1,6 |
0,4452 |
2,26 |
0,4881 |
||||
|
0,55 |
0,2088 |
1,08 |
0,3599 |
1,61 |
0,4463 |
2,28 |
0,4887 |
||||
|
0,56 |
0,2123 |
1,09 |
0,3621 |
1,62 |
0,4474 |
2,3 |
0,4893 |
||||
|
0,57 |
0,2157 |
1,1 |
0,3643 |
1,63 |
0,4484 |
2,32 |
0,4898 |
||||
|
0,58 |
0,219 |
1,11 |
0,3665 |
1,64 |
0,4495 |
2,34 |
0,4904 |
||||
|
0,59 |
0,2224 |
1,12 |
0,3686 |
1,65 |
0,4505 |
2,36 |
0,4908 |
||||
|
0,6 |
0,2257 |
1,13 |
0,3708 |
1,66 |
0,4515 |
2,38 |
0,4913 |
||||
|
0,61 |
0,2291 |
1,14 |
0,3729 |
1,67 |
0,4525 |
2,4 |
0,4918 |
||||
|
0,62 |
0,2324 |
1,15 |
0,3749 |
1,68 |
0,4535 |
2,42 |
0,4922 |
||||
|
0,63 |
0,2357 |
1,16 |
0,377 |
1,69 |
0,4545 |
2,44 |
0,4927 |
||||
|
0,64 |
0,2389 |
1,17 |
0,379 |
1,7 |
0,4554 |
2,46 |
0,4931 |
||||
|
0,65 |
0,2422 |
1,18 |
0,381 |
1,71 |
0,4564 |
2,48 |
0,4934 |
||||
|
0,66 |
0,2454 |
1,19 |
0,383 |
1,72 |
0,4573 |
2,5 |
0,4938 |
||||
|
0,67 |
0,2486 |
1,2 |
0,3849 |
1,73 |
0,4582 |
2,52 |
0,4941 |
||||
|
0,68 |
0,2517 |
1,21 |
0,3869 |
1,74 |
0,4591 |
2,54 |
0,4945 |
||||
|
0,69 |
0,2549 |
1,22 |
0,3888 |
1,75 |
0,4599 |
2,56 |
0,4948 |
||||
|
0,7 |
0,258 |
1,23 |
0,3907 |
1,76 |
0,4608 |
2,58 |
0,4951 |
||||
|
0,71 |
0,2611 |
1,24 |
0,3925 |
1,77 |
0,4616 |
2,6 |
0,4953 |
||||
|
0,72 |
0,2642 |
1,25 |
0,3914 |
1,78 |
0,4625 |
2,62 |
0,4956 |
||||
|
0,73 |
0,2673 |
1,26 |
0,3962 |
1,79 |
0,4633 |
2,64 |
0,4959 |
||||
|
0,74 |
0.2703 |
1,27 |
0,398 |
1,8 |
0,4641 |
2,66 |
0,4961 |
||||
|
0,75 |
0,2734 |
1,28 |
0,3997 |
1,81 |
0,4649 |
2,68 |
0,4963 |
||||
|
0,76 |
0,2764 |
1,29 |
0,4015 |
1,82 |
0,4656 |
2,7 |
0,4965 |
||||
|
0,77 |
0,2794 |
1,3 |
0,4032 |
1,83 |
0,4664 |
2,72 |
0,4967 |
||||
|
0,78 |
0,2823 |
1,31 |
0,4049 |
1,84 |
0,4671 |
2,74 |
0,4969 |
||||
Сайт www.MatBuro.ru
©МатБюро - Решение задач по высшей математике, теории вероятностей
|
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
|
0,79 |
0,2852 |
1,32 |
0,4066 |
1,85 |
0,4678 |
2,76 |
0,4971 |
|
0,8 |
0,2881 |
1,33 |
0,4082 |
1,86 |
0,4686 |
2,78 |
0,4973 |
|
0,81 |
0,291 |
1,34 |
0,4099 |
1,87 |
0,4693 |
2,8 |
0,4974 |
|
0,82 |
0,2939 |
1,35 |
0,4115 |
1,88 |
0,4699 |
2,82 |
0,4976 |
|
0,83 |
0,2967 |
1,36 |
0,4131 |
1,89 |
0,4706 |
2,84 |
0,4977 |
|
0.84 |
0,2995 |
1,37 |
0,4147 |
1,9 |
0,4713 |
2,86 |
0,4979 |
|
0,85 |
0,3023 |
1,38 |
0,4162 |
1,91 |
0,4719 |
2,88 |
0,498 |
|
0,86 |
0,3051 |
1,39 |
0,4177 |
1,92 |
0,4726 |
2,9 |
0,4981 |
|
0,87 |
0,3078 |
1,4 |
0,4192 |
1,93 |
0,4732 |
2,92 |
0,4982 |
|
0,88 |
0,3106 |
1,41 |
0,4207 |
1,94 |
0,4738 |
2,94 |
0,4984 |
|
0,89 |
0,3133 |
1,42 |
0,4222 |
1,95 |
0,4744 |
2,96 |
0,4985 |
|
0,9 |
0,3159 |
1,43 |
0,4236 |
1,96 |
0,475 |
2,98 |
0,4986 |
|
0,91 |
0,3186 |
1,44 |
0,4251 |
1,97 |
0,4756 |
3 |
0,49865 |
|
0,92 |
0,3112 |
1,45 |
0,4265 |
1,98 |
0,4761 |
3,2 |
0,49931 |
|
0,93 |
0,3238 |
1,46 |
0,4279 |
1,99 |
0,4767 |
3,4 |
0,49966 |
|
0,94 |
0,3264 |
1,47 |
0,4292 |
2 |
0,4772 |
3,6 |
0,499841 |
|
0,95 |
0,3289 |
1,48 |
0,4306 |
2,02 |
0,4783 |
3,8 |
0,499928 |
|
0,96 |
0,3315 |
1,49 |
0,4319 |
2,04 |
0,4793 |
4 |
0,499968 |
|
0,97 |
0,334 |
1,5 |
0,4332 |
2,06 |
0,4803 |
4,5 |
0,499997 |
|
0,98 |
0,3365 |
1,51 |
0,4345 |
2,08 |
0,4812 |
5 |
0,5 |
|
0,99 |
0,3389 |
1,52 |
0,4357 |
2,1 |
0,4821 |
||
|
1 |
0,3413 |
1,53 |
0,437 |
2,12 |
0,483 |
||
|
1,01 |
0,3438 |
1,54 |
0,4382 |
2,14 |
0,4838 |
StudFiles.ru
Значение функции Лапласа .
|
x |
Ф(x) |
x |
Ф(x) |
x |
Ф(x) |
x |
Ф(x) |
x |
Ф(x) |
x |
Ф(x) |
|
0,00 |
0,00000 |
0,50 |
0,19146 |
1,00 |
0,34134 |
1,50 |
0,43319 |
2,00 |
0,47725 |
3,00 |
0,49865 |
|
0,01 |
0,00399 |
0,51 |
0,19497 |
1,01 |
0,34375 |
1,51 |
0,43448 |
2,02 |
0,47831 |
3,05 |
0,49886 |
|
0,02 |
0,00798 |
0,52 |
0,19847 |
1,02 |
0,34614 |
1,52 |
0,43574 |
2,04 |
0,47932 |
3,10 |
0,49903 |
|
0,03 |
0,01197 |
0,53 |
0,20194 |
1,03 |
0,34849 |
1,53 |
0,43699 |
2,06 |
0,48030 |
3,15 |
0,49918 |
|
0,04 |
0,01595 |
0,54 |
0,20540 |
1,04 |
0,35083 |
1,54 |
0,43822 |
2,08 |
0,48124 |
3,20 |
0,49931 |
|
0,05 |
0,01994 |
0,55 |
0,20884 |
1,05 |
0,35314 |
1,55 |
0,43943 |
2,10 |
0,48214 |
3,25 |
0,49942 |
|
0,06 |
0,02392 |
0,56 |
0,21226 |
1,06 |
0,35543 |
1,56 |
0,44062 |
2,12 |
0,48300 |
3,30 |
0,49952 |
|
0,07 |
0,02790 |
0,57 |
0,21566 |
1,07 |
0,35769 |
1,57 |
0,44179 |
2,14 |
0,48382 |
3,35 |
0,49960 |
|
0,08 |
0,03188 |
0,58 |
0,21904 |
1,08 |
0,35993 |
1,58 |
0,44295 |
2,16 |
0,48461 |
3,40 |
0,49966 |
|
0,09 |
0,03586 |
0,59 |
0,22240 |
1,09 |
0,36214 |
1,59 |
0,44408 |
2,18 |
0,48537 |
3,45 |
0,49972 |
|
0,10 |
0,03983 |
0,60 |
0,22575 |
1,10 |
0,36433 |
1,60 |
0,44520 |
2,20 |
0,48610 |
3,50 |
0,49977 |
|
0,11 |
0,04380 |
0,61 |
0,22907 |
1,11 |
0,36650 |
1,61 |
0,44630 |
2,22 |
0,48679 |
3,55 |
0,49981 |
|
0,12 |
0,04776 |
0,62 |
0,23237 |
1,12 |
0,36864 |
1,62 |
0,44738 |
2,24 |
0,48745 |
3,60 |
0,49984 |
|
0,13 |
0,05172 |
0,63 |
0,23565 |
1,13 |
0,37076 |
1,63 |
0,44845 |
2,26 |
0,48809 |
3,65 |
0,49987 |
|
0,14 |
0,05567 |
0,64 |
0,23891 |
1,14 |
0,37286 |
1,64 |
0,44950 |
2,28 |
0,48870 |
3,70 |
0,49989 |
|
0,15 |
0,05962 |
0,65 |
0,24215 |
1,15 |
0,37493 |
1,65 |
0,45053 |
2,30 |
0,48928 |
3,75 |
0,49991 |
|
0,16 |
0,06356 |
0,66 |
0,24537 |
1,16 |
0,37698 |
1,66 |
0,45154 |
2,32 |
0,48983 |
3,80 |
0,49993 |
|
0,17 |
0,06749 |
0,67 |
0,24857 |
1,17 |
0,37900 |
1,67 |
0,45254 |
2,34 |
0,49036 |
3,85 |
0,49994 |
|
0,18 |
0,07142 |
0,68 |
0,25175 |
1,18 |
0,38100 |
1,68 |
0,45352 |
2,36 |
0,49086 |
3,90 |
0,49995 |
|
0,19 |
0,07535 |
0,69 |
0,25490 |
1,19 |
0,38298 |
1,69 |
0,45449 |
2,38 |
0,49134 |
3,95 |
0,49996 |
|
0,20 |
0,07926 |
0,70 |
0,25804 |
1,20 |
0,38493 |
1,70 |
0,45543 |
2,40 |
0,49180 |
4,00 |
0,49997 |
|
0,21 |
0,08317 |
0,71 |
0,26115 |
1,21 |
0,38686 |
1,71 |
0,45637 |
2,42 |
0,49224 |
4,05 |
0,49997 |
|
0,22 |
0,08706 |
0,72 |
0,26424 |
1,22 |
0,38877 |
1,72 |
0,45728 |
2,44 |
0,49266 |
4,10 |
0,49998 |
|
0,23 |
0,09095 |
0,73 |
0,26730 |
1,23 |
0,39065 |
1,73 |
0,45818 |
2,46 |
0,49305 |
4,15 |
0,49998 |
|
0,24 |
0,09483 |
0,74 |
0,27035 |
1,24 |
0,39251 |
1,74 |
0,45907 |
2,48 |
0,49343 |
4,20 |
0,49999 |
|
0,25 |
0,09871 |
0,75 |
0,27337 |
1,25 |
0,39435 |
1,75 |
0,45994 |
2,50 |
0,49379 |
4,25 |
0,49999 |
|
0,26 |
0,10257 |
0,76 |
0,27637 |
1,26 |
0,39617 |
1,76 |
0,46080 |
2,52 |
0,49413 |
4,30 |
0,49999 |
|
0,27 |
0,10642 |
0,77 |
0,27935 |
1,27 |
0,39796 |
1,77 |
0,46164 |
2,54 |
0,49446 |
4,35 |
0,49999 |
|
0,28 |
0,11026 |
0,78 |
0,28230 |
1,28 |
0,39973 |
1,78 |
0,46246 |
2,56 |
0,49477 |
4,40 |
0,49999 |
|
0,29 |
0,11409 |
0,79 |
0,28524 |
1,29 |
0,40147 |
1,79 |
0,46327 |
2,58 |
0,49506 |
4,45 |
0,50000 |
|
0,30 |
0,11791 |
0,80 |
0,28814 |
1,30 |
0,40320 |
1,80 |
0,46407 |
2,60 |
0,49534 |
4,50 |
0,50000 |
|
0,31 |
0,12172 |
0,81 |
0,29103 |
1,31 |
0,40490 |
1,81 |
0,46485 |
2,62 |
0,49560 |
4,55 |
0,50000 |
|
0,32 |
0,12552 |
0,82 |
0,29389 |
1,32 |
0,40658 |
1,82 |
0,46562 |
2,64 |
0,49585 |
4,60 |
0,50000 |
|
0,33 |
0,12930 |
0,83 |
0,29673 |
1,33 |
0,40824 |
1,83 |
0,46638 |
2,66 |
0,49609 |
4,65 |
0,50000 |
|
0,34 |
0,13307 |
0,84 |
0,29955 |
1,34 |
0,40988 |
1,84 |
0,46712 |
2,68 |
0,49632 |
4,70 |
0,50000 |
|
0,35 |
0,13683 |
0,85 |
0,30234 |
1,35 |
0,41149 |
1,85 |
0,46784 |
2,70 |
0,49653 |
4,75 |
0,50000 |
|
0,36 |
0,14058 |
0,86 |
0,30511 |
1,36 |
0,41309 |
1,86 |
0,46856 |
2,72 |
0,49674 |
4,80 |
0,50000 |
|
0,37 |
0,14431 |
0,87 |
0,30785 |
1,37 |
0,41466 |
1,87 |
0,46926 |
2,74 |
0,49693 |
4,85 |
0,50000 |
|
0,38 |
0,14803 |
0,88 |
0,31057 |
1,38 |
0,41621 |
1,88 |
0,46995 |
2,76 |
0,49711 |
4,90 |
0,50000 |
|
0,39 |
0,15173 |
0,89 |
0,31327 |
1,39 |
0,41774 |
1,89 |
0,47062 |
2,78 |
0,49728 |
4,95 |
0,50000 |
|
0,40 |
0,15542 |
0,90 |
0,31594 |
1,40 |
0,41924 |
1,90 |
0,47128 |
2,80 |
0,49744 |
5,00 |
0,50000 |
|
0,41 |
0,15910 |
0,91 |
0,31859 |
1,41 |
0,42073 |
1,91 |
0,47193 |
2,82 |
0,49760 |
||
|
0,42 |
0,16276 |
0,92 |
0,32121 |
1,42 |
0,42220 |
1,92 |
0,47257 |
2,84 |
0,49774 |
||
|
0,43 |
0,16640 |
0,93 |
0,32381 |
1,43 |
0,42364 |
1,93 |
0,47320 |
2,86 |
0,49788 |
||
|
0,44 |
0,17003 |
0,94 |
0,32639 |
1,44 |
0,42507 |
1,94 |
0,47381 |
2,88 |
0,49801 |
||
|
0,45 |
0,17364 |
0,95 |
0,32894 |
1,45 |
0,42647 |
1,95 |
0,47441 |
2,90 |
0,49813 |
||
|
0,46 |
0,17724 |
0,96 |
0,33147 |
1,46 |
0,42785 |
1,96 |
0,47500 |
2,92 |
0,49825 |
||
|
0,47 |
0,18082 |
0,97 |
0,33398 |
1,47 |
0,42922 |
1,97 |
0,47558 |
2,94 |
0,49836 |
||
|
0,48 |
0,18439 |
0,98 |
0,33646 |
1,48 |
0,43056 |
1,98 |
0,47615 |
2,96 |
0,49846 |
||
|
0,49 |
0,18793 |
0,99 |
0,33891 |
1,49 |
0,43189 |
1,99 |
0,47670 |
2,98 |
0,49856 |
Для отрицательных значений Ф(-X)=-Ф(X). Для x>5 Ф(X)=0,5 . В Excel значение функции Лапласа можно вычислить с помощью формулы =НОРМСТРАСП(число) - 0,5. По своему логическому содержанию функция Лапласа Ф(X) близка к интегральной функции нормального распределения F(X), их взаимосвязь: Ф(X) = F(X) - 0,5
StudFiles.ru
2. Таблица значений большой функции Лапласа
|
x |
Ф(x) |
x |
Ф(x) |
x |
Ф(x) |
x |
Ф(x) |
|
0,00 |
0,0000 |
0,33 |
0,1293 |
0,66 |
0,2454 |
0,99 |
0,3389 |
|
0,01 |
0,0040 |
0,34 |
0,1331 |
0,67 |
0,2486 |
1,00 |
0,3413 |
|
0,02 |
0,0080 |
0,35 |
0,1368 |
0,68 |
0,2517 |
1,01 |
0,3438 |
|
0,03 |
0,0120 |
0,36 |
0,1406 |
0,69 |
0,2549 |
1,02 |
0,3461 |
|
0,04 |
0,0160 |
0,37 |
0,1443 |
0,70 |
0,2580 |
1,03 |
0,3485 |
|
0,05 |
0,0199 |
0,38 |
0,1480 |
0,71 |
0,2611 |
1,04 |
0,3508 |
|
0,06 |
0,0239 |
0,39 |
0,1517 |
0,72 |
0,2642 |
1,05 |
0,3531 |
|
0,07 |
0,0279 |
0,40 |
0,1554 |
0,73 |
0,2673 |
1,06 |
0,3554 |
|
0,08 |
0,0319 |
0,41 |
0,1591 |
0,74 |
0,2703 |
1,07 |
0,3577 |
|
0,09 |
0,0359 |
0,42 |
0,1628 |
0,75 |
0,2734 |
1,08 |
0,3599 |
|
0,10 |
0,0398 |
0,43 |
0,1664 |
0,76 |
0,2764 |
1,09 |
0,3621 |
|
0,11 |
0,0438 |
0,44 |
0,1700 |
0,77 |
0,2794 |
1,10 |
0,3643 |
|
0,12 |
0,0478 |
0,45 |
0,1736 |
0,78 |
0,2823 |
1,11 |
0,3665 |
|
0,13 |
0,0517 |
0,46 |
0,1772 |
0,79 |
0,2852 |
1,12 |
0,3686 |
|
0,14 |
0,0557 |
0,47 |
0,1808 |
0,80 |
0,2881 |
1,13 |
0,3708 |
|
0,15 |
0,0596 |
0,48 |
0,1844 |
0,81 |
0,2910 |
1,14 |
0,3729 |
|
0,16 |
0,0636 |
0,49 |
0,1879 |
0,82 |
0,2939 |
1,15 |
0,3749 |
|
0,17 |
0,0675 |
0,50 |
0,1915 |
0,83 |
0,2967 |
1,16 |
0,3770 |
|
0,18 |
0,0714 |
0,51 |
0,1950 |
0,84 |
0,2995 |
1,17 |
0,3790 |
|
0,19 |
0,0753 |
0,52 |
0,1985 |
0,85 |
0,3023 |
1,18 |
0,3810 |
|
0,20 |
0,0793 |
0,53 |
0,2019 |
0,86 |
0,3051 |
1,19 |
0,3830 |
|
0,21 |
0,0832 |
0,54 |
0,2054 |
0,87 |
0,3078 |
1,20 |
0,3849 |
|
0,22 |
0,0871 |
0,55 |
0,2088 |
0,88 |
0,3106 |
1,21 |
0,3869 |
|
0,23 |
0,0910 |
0,56 |
0,2123 |
0,89 |
0,3133 |
1,22 |
0,3883 |
|
0,24 |
0,0948 |
0,57 |
0,2157 |
0,90 |
0,3159 |
1,23 |
0,3907 |
|
0,25 |
0,0987 |
0,58 |
0,2190 |
0,91 |
0,3186 |
1,24 |
0,3925 |
|
0,26 |
0,1026 |
0,59 |
0,2224 |
0,92 |
0,3212 |
1,25 |
0,3944 |
|
0,27 |
0,1064 |
0,60 |
0,2257 |
0,93 |
0,3238 |
1,26 |
0,3962 |
|
0,28 |
0,1103 |
0,61 |
0,2291 |
0,94 |
0,3264 |
1,27 |
0,3980 |
|
0,29 |
0,1141 |
0,62 |
0,2324 |
0,95 |
0,3289 |
1,28 |
0,3997 |
|
0,30 |
0,1179 |
0,63 |
0,2357 |
0,96 |
0,3315 |
1,29 |
0,4015 |
|
0,31 |
0,1217 |
0,64 |
0,2389 |
0,97 |
0,3340 |
1,30 |
0,4032 |
|
0,32 |
0,1255 |
0,65 |
0,2422 |
0,98 |
0,3365 |
1,31 |
0,4049 |
|
1,32 |
0,4066 |
1,66 |
0,4515 |
2,00 |
0,4772 |
2,68 |
0,4963 |
|
1,33 |
0,4082 |
1,67 |
0,4525 |
2,02 |
0,4783 |
2,70 |
0,4965 |
|
1,34 |
0,4099 |
1,68 |
0,4535 |
2,04 |
0,4793 |
2,72 |
0,4967 |
|
1,35 |
0,4115 |
1,69 |
0,4545 |
2,06 |
0,4803 |
2,74 |
0,4969 |
|
1,36 |
0,4131 |
1,70 |
0,4554 |
2,08 |
0,4812 |
2,76 |
0,4971 |
|
1,37 |
0,4147 |
1,71 |
0,4564 |
2,10 |
0,4821 |
2,78 |
0,4973 |
|
1,38 |
0,4162 |
1,72 |
0,4573 |
2,12 |
0,4830 |
2,80 |
0,4974 |
|
1,39 |
0,4177 |
1,73 |
0,4582 |
2,14 |
0,4838 |
2,82 |
0,4976 |
|
1,40 |
0,4192 |
1,74 |
0,4591 |
2,16 |
0,4846 |
2,84 |
0,4977 |
|
1,41 |
0,4207 |
1,75 |
0,4599 |
2,18 |
0,4854 |
2,86 |
0,4979 |
|
1,42 |
0,4222 |
1,76 |
0,4608 |
2,20 |
0,4861 |
2,88 |
0,4980 |
|
1,43 |
0,4236 |
1,77 |
0,4616 |
2,22 |
0,4868 |
2,90 |
0,4981 |
|
1,44 |
0,4251 |
1,78 |
0,4625 |
2,24 |
0,4875 |
2,92 |
0,4982 |
|
1,45 |
0,4265 |
1,79 |
0,4633 |
2,26 |
0,4881 |
2,94 |
0,4984 |
|
1,46 |
0,4279 |
1,80 |
0,4641 |
2,28 |
0,4887 |
2,96 |
0,4985 |
|
1,47 |
0,4292 |
1,81 |
0,4649 |
2,30 |
0,4893 |
2,98 |
0,4986 |
|
1,48 |
0,4306 |
1,82 |
0,4656 |
2,32 |
0,4898 |
3,00 |
0,49865 |
|
1,49 |
0,4319 |
1,83 |
0,4664 |
2,34 |
0,4904 |
3,20 |
0,49931 |
|
1,50 |
0,4332 |
1,84 |
0,4671 |
2,36 |
0,4909 |
3,40 |
0,49966 |
|
1,51 |
0,4345 |
1,85 |
0,4678 |
2,38 |
0,4913 |
3,60 |
0,499841 |
|
1,52 |
0,4357 |
1,86 |
0,4686 |
2,40 |
0,4918 |
3,80 |
0,499928 |
|
1,53 |
0,4370 |
1,87 |
0,4693 |
2.42 |
0,4922 |
4,00 |
0,499968 |
|
1,54 |
0,4382 |
1,88 |
0,4699 |
2,44 |
0,4927 |
4,50 |
0,499997 |
|
1,55 |
0,4394 |
1,89 |
0,4706 |
2,46 |
0,4931 |
5,00 |
0,499997 |
|
1,56 |
0,4406 |
1,90 |
0,4713 |
2,48 |
0,4934 |
||
|
1,57 |
0,4418 |
1,91 |
0,4719 |
2,50 |
0,4938 |
||
|
1,58 |
0,4429 |
1,92 |
0,4746 |
2,52 |
0,4941 |
||
|
1,59 |
0,4441 |
1,93 |
0,4732 |
2,54 |
0,4945 |
||
|
1,60 |
0,4452 |
1,94 |
0,4738 |
2,56 |
0,4948 |
||
|
1,61 |
0,4463 |
1,95 |
0,4744 |
2,58 |
0,4951 |
||
|
1,62 |
0,4474 |
1,96 |
0,4750 |
2,60 |
0,4953 |
||
|
1,63 |
0,4484 |
1,97 |
0,4756 |
2,62 |
0,4956 |
||
|
1,64 |
0,4495 |
1,98 |
0,4761 |
2,64 |
0,4959 |
||
|
1,65 |
0,4505 |
1,99 |
0,4767 |
2,66 |
0,4961 |
StudFiles.ru
6.2. Локальная и интегральная теоремы Лапласа
Выше мы рассмотрели формулу Бернулли, которая позволяет находить вероятность появления события в ![]() испытаниях
испытаниях![]() раз. Эту формулу удобно использовать в тех случаях, когда число испытаний
раз. Эту формулу удобно использовать в тех случаях, когда число испытаний![]() невелико. Если же, например, надо найтиP50(30), то в этом случае сталкиваемся с вычислением
невелико. Если же, например, надо найтиP50(30), то в этом случае сталкиваемся с вычислением![]() . Но даже не все современные калькуляторы могут вычислить это значение. При использовании стандартной записи числа приходится делать округления, отбрасывая значащие цифры, что приводит в процессе вычислений к накоплению погрешностей.
. Но даже не все современные калькуляторы могут вычислить это значение. При использовании стандартной записи числа приходится делать округления, отбрасывая значащие цифры, что приводит в процессе вычислений к накоплению погрешностей.
Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно kраз вnиспытаниях, если число испытаний достаточно велико.
Заметим, что для частного случая, а именно для p=1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольногоp, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь иногда называют теоремой Муавра – Лапласа.
Мы приведем только формулировку этой теоремы, опуская ее доказательство.
Теорема 6.1 (локальная теорема Лапласа).
Если вероятность pпоявления событияAв каждом испытании постоянно и отличается от нуля и единицы, то вероятностьPn(k) того, что событиеAпоявится вnиспытаниях ровноkраз, приближенно равна (тем точнее, чем большеn):
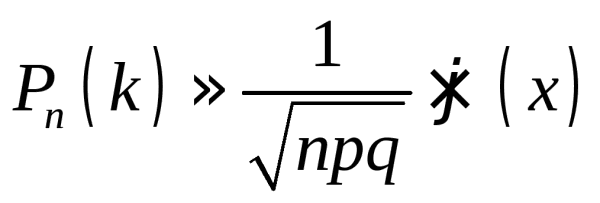 , где
, где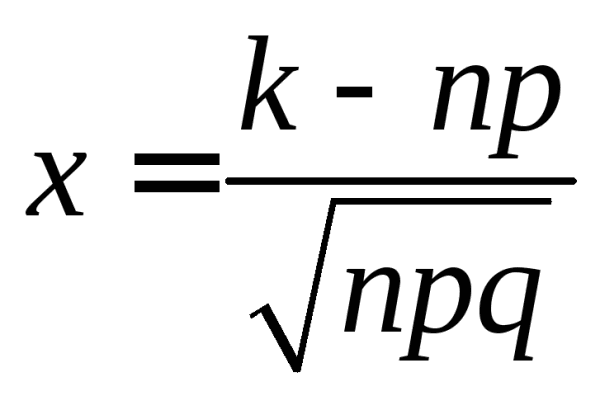 . (6.2)
. (6.2)
Функция ![]() называется малой функций Лапласа. Значения функции(x), соответствующие положительному значению аргумента
называется малой функций Лапласа. Значения функции(x), соответствующие положительному значению аргумента![]() , определяется из соответствующей таблицы. Для отрицательных значений аргумента пользуются той же таблицей, так как(x) четная функция, т.е.
, определяется из соответствующей таблицы. Для отрицательных значений аргумента пользуются той же таблицей, так как(x) четная функция, т.е. ![]() .
.
Вновь предположим, что производится ![]() испытаний, в каждом из которых вероятность появления события
испытаний, в каждом из которых вероятность появления события![]() постоянна и равна
постоянна и равна![]() . Как вычислить вероятность
. Как вычислить вероятность![]() того, что событие
того, что событие![]() появится вnиспытаниях не менее
появится вnиспытаниях не менее![]() и не более
и не более![]() раз (для краткости будем говорить «от
раз (для краткости будем говорить «от![]() до
до![]() раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим, опустив доказательство.
раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим, опустив доказательство.
Теорема 6.2 (интегральная теорема Лапласа).
Если вероятность ![]() появления события
появления события![]() в каждом испытании постоянно и отличается от нуля и единицы, то вероятность
в каждом испытании постоянно и отличается от нуля и единицы, то вероятность![]() того, что событие
того, что событие![]() появится вnиспытаниях от
появится вnиспытаниях от![]() до
до![]() раз, приближенно равна:
раз, приближенно равна:
![]() , где
, где![]() . (6.3)
. (6.3)
Функция 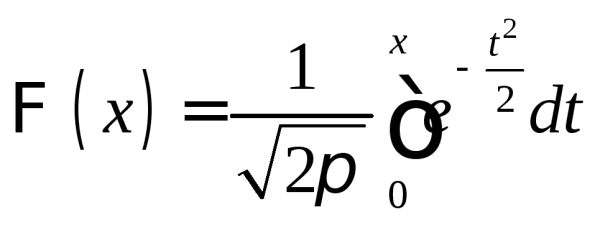 называется функций Лапласа. Значения функции(x), соответствующие положительному значению аргумента
называется функций Лапласа. Значения функции(x), соответствующие положительному значению аргумента![]() и
и![]() , определяется из соответствующей таблицы. Для отрицательных значений аргумента можно пользоваться той же таблицей, так как(x) нечетная функция, т.е.
, определяется из соответствующей таблицы. Для отрицательных значений аргумента можно пользоваться той же таблицей, так как(x) нечетная функция, т.е.![]() . В таблице приводятся значения лишь до
. В таблице приводятся значения лишь до![]() . При
. При![]() можно принять
можно принять![]() .
.
Замечание. Локальной и интегральной теоремами Лапласа на практике удобно пользоваться в случае, если npq>10. Если же npq
Пример 6.4.Вероятность появления событияAв каждом из 900 независимых испытаний равнаp=0,8. Найти вероятность того, что событиеAпроизойдет:
а) 750 раз;
б) не менее 710 раз и не более 740 раз.
Решение.а) Из условия следует, чтоn=900,k=750,p=0,8, поэтомуq=0,2. Посколькуnpq=9000,80,2=144>10, то можно воспользоваться локальной теоремой Лапласа.
Находим x:
![]() .
.
По таблице значений функции находим (2,5)=0,0175.
Согласно локальной теореме Лапласа получаем искомую вероятность:
![]() .
.
б) Из условия следует, что n=900,k1=710,k2=740,p=0,8, поэтомуq=0,2. Находимx1иx2:
![]() ;
;
![]() .
.
По таблице значений функции Лапласа, учитывая нечетность функции, определяем
(x1)=(0,83)=0,2967;
(x2)=(1,67)=0,4525.
Согласно интегральной теореме Лапласа получаем искомую вероятность:
![]() .
.
StudFiles.ru
Локальная и интегральная теоремы Лапласа
Очевидно, что при больших значениях n пользоваться формулой Бернулли затруднительно, так как придется вычислять значения факториалов больших чисел и возводить в большую степень числа, близкие к нулю (0 < p < 1). В этом случае можно использовать асимптотические формулы Лапласа, дающие тем лучшее приближенное значение Pn(m) и Pn(k1 £ m £ k2), чем больше n.
Локальная теорема Лапласа.Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний ровно m раз приближенно равна (тем точнее, чем больше n) значению функции
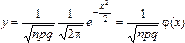 ,
, 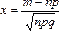 .
.
(В приложении A приведена таблица значений функции 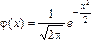 , соответствующих положительным значениям аргумента.)
, соответствующих положительным значениям аргумента.)
Функция j(x) является четной функцией, то есть j(– x) = j(x), для всех 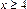 принимается j( x) = 0. Таким образом, вероятность того, что событие A появится в n независимых испытаниях ровно m раз, приближенно равна
принимается j( x) = 0. Таким образом, вероятность того, что событие A появится в n независимых испытаниях ровно m раз, приближенно равна
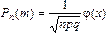 , (11)
, (11)
где 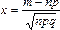 .
.
Интегральная теорема Лапласа.Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний от k1 до k2 раз, приближенно равна
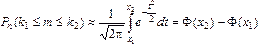 , (12)
, (12)
где 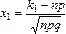 ,
, 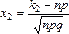 .
.
В приложении Б приведены таблицы значений функции Лапласа
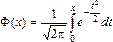 .
.
Функция F(x) нечетна, то есть F(– x) = – F(x). При x > 5 можно принять F(x) = 0,5.
Пример 21Завод изготавливает конденсаторы. Вероятность выхода из строя за время Т одного конденсатора равна 0,2. Найти вероятность того, что из 100 конденсаторов за время Т выйдет из строя: а) ровно 10 конденсаторов; б) не менее 20 и не более100 конденсаторов.
Решение. Определим события В = {среди 100 конденсаторов ровно 20 выйдет из строя за время Т}; С ={среди 100 конденсаторов за время Т из строя выйдет не менее 20 и не более100}.
Предполагая, что выход из строя конденсаторов осуществляется независимо друг от друга, условие задачи можно рассматривать как серию из n = 100 независимых испытаний, в каждом из которых вероятность события A = {конденсатор выйдет из строя} равна 0,2. То есть p = 0,2, q = 0,8.
Так как число испытаний достаточно велико, для вычисления вероятностей событий B и C можно воспользоваться приближёнными формулами Муавра-Лапласа.
а) Определим вероятность события В = {среди 100 конденсаторов ровно 10 выйдет из строя за время Т}.
Для вычисления вероятности события В воспользуемся локальной теоремой Муавра-Лапласа. В данном случае: n = 100; p = 0,2; q = 0,8; m = 10;
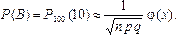
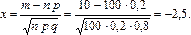
По таблицам значений функции 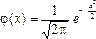 находим
находим
j ( – 2,5) = 0,0175;
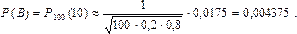
б) Для вычисления вероятности события С воспользуемся интегральной теоремой Муавра-Лапласа при n = 100; p = 0,2; q = 1 – 0,2= 0,8; k1 = 20; k2 =100;
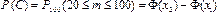 ;
;
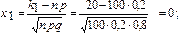
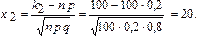
По таблицам значений функции 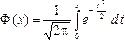 находим
находим
F (0) = 0, F (20) = 0,5.
Таким образом, 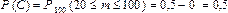 .
.
studopedia.ru
Как пользоваться таблицей интегральной функции Лапласа?
Здравствуйте. Возникли вопросы по таблице значений интегральной функции Лапласа
Ф (8,107)=0, потому что 8,107>4. Верно?
Чему равно Ф (-1,506) ?
Заранее спасибо.
Cooler viktor ▶
Таблицами значений интегральной функции Лапласа нынче никто не пользуется. Вместо этого тупо вычисляют интеграл, через который эта функция выражается. Примерно так:
Тыкаешь СЮДА, в появиившемся окне нажимаешь МОДЕРН ВИД, затем с помощью вывлившеся виртуальной клавиатуры набиваешь нужный интеграл (делить -- это косая черта / рядом с правой клавишей SHIFT, умножить -- снежинка *, нажимаешь SHIFT+цифра 8):

Тыкаешь ВЫЧИСЛИТЬ ИНТЕГРАЛ и получаешь ответ:

☛ Не забывай о свойстве: Ф (-x) = -Ф (x)
☛ НО! ! С числом 8,107 получается не совсем хорошо. Онлайн калькулятор выдает:

А должен выдавать: 0,999999999999999999999999999999999999...
И в каком-нибудь пятидесятом знаке после запятой должна быть не девятка, а другая цифра. А оно простым инженерам надо? Нет. Поэтому тупо бери для интегральной функции Лапласа Ф (8,107)=1.
Всего доброго, успехов в учебе. ☺
☛ Я под функцией Лапласа Ф (х) подразумевал интеграл от -х до +х.
Но часто подразумевают интеграл от нуля до х (например, х=8,107).
Если брать такой интеграл (т. е. от нуля до 8,107), то получится число, в два раза меньшее чем у меня, т. е. Ф (8,107)=0,5, а не Ф (8,107)=1.
Точно так же будет Ф (-1,506)=-0,433967.
Читайте также
![Таблица значений функции Таблица значений функции]() Таблица значений функции
Таблица значений функции![Таблица значений критерия стьюдента t критерия Таблица значений критерия стьюдента t критерия]() Таблица значений критерия стьюдента t критерия
Таблица значений критерия стьюдента t критерия- Разряды наречий по значению таблица с примерами
![Таблица критических значений спирмена Таблица критических значений спирмена]() Таблица критических значений спирмена
Таблица критических значений спирмена![Таблица критических значений манна уитни Таблица критических значений манна уитни]() Таблица критических значений манна уитни
Таблица критических значений манна уитни![Таблица критических значений пирсона Таблица критических значений пирсона]() Таблица критических значений пирсона
Таблица критических значений пирсона![Как найти область значения функции Как найти область значения функции]() Как найти область значения функции
Как найти область значения функции![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского- 7 Треф значение
![Славянские имена мальчиков и их значение Славянские имена мальчиков и их значение]() Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия
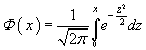 Таблица значений функции
Таблица значений функции Таблица значений критерия стьюдента t критерия
Таблица значений критерия стьюдента t критерия Таблица критических значений спирмена
Таблица критических значений спирмена Таблица критических значений манна уитни
Таблица критических значений манна уитни Таблица критических значений пирсона
Таблица критических значений пирсона Как найти область значения функции
Как найти область значения функции Аутентичность значение слова
Аутентичность значение слова Чувак значение слова с еврейского
Чувак значение слова с еврейского Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение Барыга значение слова википедия
Барыга значение слова википедия