t-критерий Стьюдента для зависимых выборок
Метод позволяет проверить гипотезу о том, что средние значения двух генеральных совокупностей, из которых извлечены сравниваемые зависимые выборки, отличаются друг от друга. Допущение зависимости чаще всего значит, что признак измерен на одной и той же выборке дважды, например, до воздействия и после него. В общем же случае каждому представителю одной выборки поставлен в соответствие представитель из другой выборки (они попарно объединены) так, что два ряда данных положительно коррелируют друг с другом. Более слабые виды зависимости выборок: выборка 1 — мужья, выборка 2 — их жены; выборка 1 — годовалые дети, выборка 2 составлена из близнецов детей выборки 1, и т. д.
Проверяемая статистическая гипотеза, как и в предыдущем случае, Н0: М1 = М2 (средние значения в выборках 1 и 2 равны).При ее отклонении принимается альтернативная гипотеза о том, что М1 больше (меньше) М2.
Исходные предположения для статистической проверки:
□ каждому представителю одной выборки (из одной генеральной совокупности) поставлен в соответствие представитель другой выборки (из другой генеральной совокупности);
□ данные двух выборок положительно коррелируют (образуют пары);
□ распределение изучаемого признака и в той и другой выборке соответствует нормальному закону.
Структура исходных данных: имеется по два значения изучаемого признака для каждого объекта (для каждой пары).
Ограничения: распределения признака и в той, и в другой выборке должно существенно не отличаться от нормального; данные двух измерений, соответствующих той и другой выборке, положительно коррелируют.
Альтернативы: критерий Т-Вилкоксона, если распределение хотя бы для одной выборки существенно отличается от нормального; критерий t-Стьюдента для независимых выборок — если данные для двух выборок не коррелируют положительно.
Формула для эмпирического значения критерия t-Стьюдента отражает тот факт, что единицей анализа различий является разность (сдвиг) значений признака для каждой пары наблюдений. Соответственно, для каждой из N пар значений признака сначала вычисляется разность di = х1i - x2i.
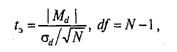
(3)где Md – средняя разность значений; σd – стандартное отклонение разностей.
Пример расчета:
Предположим, в ходе проверки эффективности тренинга каждому из 8 членов группы задавался вопрос «Насколько часто твое мнение совпадаете мнением группы?» — дважды, до и после тренинга. Для ответов использовалась 10-балльная шкала: 1 — никогда, 5 — в половине случаев, 10 — всегда. Проверялась гипотеза о том, что в результате тренинга самооценка конформизма (стремления быть как другие в группе) участников возрастет (α = 0,05). Составим таблицу для промежуточных вычислений (таблица 3).
Таблица 3

Среднее арифметической для разности Md = (-6)/8= -0,75. Вычтем это значение из каждого d (предпоследний столбец таблицы).
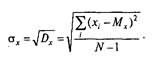 Формула для стандартного отклонения отличается лишь тем, что вместо Х в ней фигурирует d.Подставляем все нужные значения, получаем
Формула для стандартного отклонения отличается лишь тем, что вместо Х в ней фигурирует d.Подставляем все нужные значения, получаем
σd = 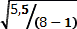 = 0,886.
= 0,886.
Ш а г 1. Вычисляем эмпирическое значение критерия по формуле (3): средняя разность Md = -0,75; стандартное отклонение σd = 0,886; tэ = 2,39; df =7.
 Ш а г 2. Определяем по таблице критических значений критерия t-Стьюдента р-уровень значимости. Для df = 7 эмпирическое значение находится между критическими для р = 0,05 и р — 0,01. Следовательно, р < 0,05.
Ш а г 2. Определяем по таблице критических значений критерия t-Стьюдента р-уровень значимости. Для df = 7 эмпирическое значение находится между критическими для р = 0,05 и р — 0,01. Следовательно, р < 0,05.
| df | Р | ||
| 0,05 | 0,01 | 0,001 | |
| 2,365 | 3,499 | 5,408 |
Ш а г 3. Принимаем статистическое решение и формулируем вывод. Статистическая гипотеза о равенстве средних значений отклоняется. Вывод: показатель самооценки конформизма участников после тренинга увеличился статистически достоверно (на уровне значимости р < 0,05).
К параметрическим методам относится и сравнение дисперсий двух выборок по критерию F-Фишера.Иногда этот метод приводит к ценным содержательным выводам, а в случае сравнения средних для независимых выборок сравнение дисперсий является обязательной процедурой.
Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая знаменателе.
Сравнение дисперсий. Метод позволяет проверить гипотезу о том, что дисперсии двух генеральных совокупностей, из которых извлечены сравниваемые выборки, отличаются друг от друга. Проверяемая статистическая гипотеза Н0: σ12 = σ22 (дисперсия в выборке 1 равна дисперсии в выборке 2). При ее отклонении принимается альтернативная гипотеза о том, что одна дисперсия больше другой.
Исходные предположения: две выборки извлекаются случайно из разных генеральных совокупностей с нормальным распределением изучаемого признака.
Структура исходных данных: изучаемый признак измерен у объектов (испытуемых), каждый из которых принадлежит к одной из двух сравниваемых выборок.
Ограничения: распределения признака и в той, и в другой выборке существенно не отличаются от нормального.
Альтернатива методу: критерий Ливена (Levene'sTest), применение которого не требует проверки предположения о нормальности (используется в программе SPSS).
Формула для эмпирического значения критерия F-Фишера:
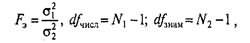 (4)
(4)
где σ12 — большая дисперсия, a σ22— меньшая дисперсия. Так как заранее не известно, какая дисперсия больше, то для определения р-уровня применяется Таблица критических значений для ненаправленных альтернатив. Если Fэ > FKp для соответствующего числа степеней свободы, то р < 0,05 и статистическую гипотезу о равенстве дисперсий можно отклонить (для α = 0,05).
Пример расчета:
Детям давались обычные арифметические задания, после чего одной случайно выбранной половине учащихся сообщали, что они не выдержали испытания, а остальным — обратное. Затем у каждого ребенка спрашивали, сколько секунд ему потребовалось бы для решения аналогичной задачи. Экспериментатор вычислял разность между называемым ребенком временем и результатом выполненного задания (в сек.). Ожидалось, что сообщение о неудаче вызовет некоторую неадекватность самооценки ребенка. Проверяемая гипотеза (на уровне α = 0,005) состояла в том, что дисперсия совокупности самооценок не зависит от сообщений об удаче или неудаче (Н0: σ12=σ22).
Были получены следующие данные:
 |
Ш а г 1. Вычислим эмпирическое значение критерия и числа степеней свободы по формулам (4):

Шаг 2. По таблице критических значений критерия f-Фишера для ненаправленных альтернатив находим критическое значение для dfчисл = 11; dfзнам = 11. Однако критическое значение есть только для dfчисл = 10 и dfзнам = 12. Большее число степеней свободы брать нельзя, поэтому берем критическое значение для dfчисл = 10: Для р = 0,05 FKp = 3,526; для р = 0,01 FKp = 5,418.
Ш а г 3. Принятие статистического решения и содержательный вывод. Поскольку эмпирическое значение превышает критическое значение для р = 0,01 (и тем более — для р = 0,05), то в данном случае р < 0,01 и принимается альтернативная гипотеза: дисперсия в группе 1 превышает дисперсию в группе 2 (р < 0,01). Следовательно, после сообщения о неудаче неадекватность самооценки выше, чем после сообщения об удаче.
studopedia.ru
/ практикум-статистика / справочные материалы / значения t-критерия стьюдента
Значениеt-критерия Стьюдента при уровне значимости 0,10, 0,05 и 0,01
|
ν |
|
ν |
|
||||
|
0,10 |
0,05 |
0,01 |
0,10 |
0,05 |
0,01 |
||
|
1 |
6,3138 |
12,706 |
63,657 |
18 |
1,7341 |
2,1009 |
2,8784 |
|
2 |
2,9200 |
4,3027 |
9,9248 |
19 |
1,7291 |
2,0930 |
2,8609 |
|
3 |
2,3534 |
3,1825 |
5,8409 |
20 |
1,7247 |
2,0860 |
2,8453 |
|
4 |
2,1318 |
2,7764 |
4,6041 |
21 |
1,7207 |
2,0796 |
2,8314 |
|
5 |
2,0150 |
2,5706 |
4,0321 |
22 |
1,7171 |
2,0739 |
2,8188 |
|
6 |
1,9432 |
2,4469 |
3,7074 |
23 |
1,7139 |
2,0687 |
2,8073 |
|
7 |
1,8946 |
2,3646 |
3,4995 |
24 |
1,7109 |
2,0639 |
2,7969 |
|
8 |
1,8595 |
2,3060 |
3,3554 |
25 |
1,7081 |
2,0595 |
2,7874 |
|
9 |
1,8331 |
2,2622 |
3,2498 |
26 |
1,7056 |
2,0555 |
2,7757 |
|
10 |
1,8125 |
2,2281 |
3,1693 |
27 |
1,7033 |
2,0518 |
2,7707 |
|
11 |
1,7959 |
2,2010 |
3,1058 |
28 |
1,7011 |
2,0484 |
2,7633 |
|
12 |
1,7823 |
2,1788 |
3,0545 |
29 |
1,6991 |
2,0452 |
2,7564 |
|
13 |
1,7709 |
2,1604 |
3,0123 |
30 |
1,6973 |
2,0423 |
2,7500 |
|
14 |
1,7613 |
2,1448 |
2,9768 |
40 |
1,6839 |
2,0211 |
2,7045 |
|
15 |
1,7530 |
2,1315 |
2,9467 |
60 |
1,6707 |
2,0003 |
2,6603 |
|
16 |
1,7459 |
2,1199 |
2,9208 |
120 |
1,6577 |
1,9799 |
2,6174 |
|
17 |
1,7396 |
2,1098 |
2,8982 |
|
1,6449 |
1,9600 |
2,5758 |
ν – степени свободы вариации
StudFiles.ru
Стандартные значения критерия Стьюдента
|
Число степеней свободы |
Уровни значимости |
Число степеней свободы |
Уровни значимости |
||||||
|
0,95 |
0,99 |
0,999 |
0,95 |
0,99 |
0,999 |
||||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 2,14 2,13 2,12 2,11 2,10 |
63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 3,01 2,98 2,95 2,92 2,90 2,88 |
636,62 31,60 12,94 8,61 6,86 5,96 5,40 5,04 4,78 4,59 4,49 4,32 4,22 4,14 4,07 4,01 3,96 3,92 |
19 20 21 22 23 24 25 26 27 28 29 30 35 40 60 120 ¥ |
2,09 2,08 2,07 2,06 2,06 2,05 2,05 2,04 2,02 2,00 1,98 1,96 |
2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,70 2,66 2,62 2,58 |
3,88 3,85 3,82 3,79 3,77 3,74 3,72 3,71 3,69 3,66 3,66 3,65 3,55 3,46 3,37 3,29 |
||
Таблица XI
Стандартные значения критерия Фишера, используемые для оценки достоверности различий между двумя выборками
|
Степени свободы (n) |
Уровень значимости |
Степени свободы (n) |
Уровень значимости |
||||
|
0,95 |
0,99 |
0,999 |
0,95 |
0,99 |
0,999 |
||
|
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
10,13 7,71 6,61 5,99 5,59 5,32 5,12 4,96 4,84 4,75 4,67 4,60 4,54 4,49 4,45 4,41 4,38 4,35 4,32 4,30 4,28 4,26 4,24 4,22 4,21 |
34,12 21,20 16,26 13,74 12,25 11,26 10,56 10,04 9,65 9,33 9,07 8,86 8,68 8,53 8,40 8,28 8,18 8,10 8,02 7,94 7,88 7,82 7,77 7,72 7,68 |
167,5 74,1 47,0 35,5 29,2 25,4 22,9 21,0 19,7 18,6 17,8 17,1 16,6 16,1 15,7 15,4 15,1 14,8 14,6 14,4 14,2 14,0 13,9 13,7 13,6 |
28 29 30 32 34 36 38 40 42 44 46 48 50 55 60 65 70 80 100 125 150 200 400 1000 ¥ |
4,20 4,18 4,17 4,15 4,13 4,11 4,10 4,08 4,07 4,06 4,05 4,04 4,03 4,02 4,00 3,99 3,98 3,96 3,94 3,92 3,91 3,89 3,86 3,85 3,84 |
7,64 7,60 7,56 7,50 7,44 7,39 7,35 7,31 7,27 7,24 7,21 7,19 7,17 7,12 7,08 7,04 7,01 6,96 6,90 6,84 6,81 6,76 6,70 6,66 6,64 |
13,5 13,4 13,3 13,2 13,1 13,0 12,9 12,8 12,7 12,5 12,4 12,3 12,2 12,1 12,0 11,9 11,6 11,5 11,4 11,3 11,2 11,0 10,9 10,8 |
Таблица XII
StudFiles.ru
t-Критерий Стьюдента
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
t-статистика строится обычно по следующему общему принципу: в числителе случайная величина с нулевым математическим ожиданием (при выполнении нулевой гипотезы), а в знаменателе — выборочное стандартное отклонение этой случайной величины, получаемое как квадратный корень из несмешенной оценки дисперсии.
История
Данный критерий был разработан Уильямом Госсетом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
Требования к данным
Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.
Требование нормальности распределения данных является необходимым для точного t {\displaystyle t} -теста. Однако, даже при других распределениях данных возможно использование t {\displaystyle t} -статистики. Во многих случаях эта статистика асимптотически имеет стандартное нормальное распределение — N ( 0 , 1 ) {\displaystyle N(0,1)} , поэтому можно использовать квантили этого распределения. Однако, часто даже в этом случае используют квантили не стандартного нормального распределения, а соответствующего распределения Стьюдента, как в точном t {\displaystyle t} -тесте. Асимптотически они эквивалентны, однако на малых выборках доверительные интервалы распределения Стьюдента шире и надежнее.
Одновыборочный t-критерий
Применяется для проверки нулевой гипотезы H 0 : E ( X ) = m {\displaystyle H_{0}:E(X)=m} о равенстве математического ожидания E ( X ) {\displaystyle E(X)} некоторому известному значению m {\displaystyle m} .
Очевидно, при выполнении нулевой гипотезы E ( X ¯ ) = m {\displaystyle E({\overline {X}})=m} . С учётом предполагаемой независимости наблюдений V ( X ¯ ) = σ 2 / n {\displaystyle V({\overline {X}})=\sigma ^{2}/n} . Используя несмещенную оценку дисперсии s X 2 = ∑ t = 1 n ( X t − X ¯ ) 2 / ( n − 1 ) {\displaystyle s_{X}^{2}=\sum _{t=1}^{n}(X_{t}-{\overline {X}})^{2}/(n-1)} получаем следующую t-статистику:
t = X ¯ − m s X / n {\displaystyle t={\frac {{\overline {X}}-m}{s_{X}/{\sqrt {n}}}}}
При нулевой гипотезе распределение этой статистики t ( n − 1 ) {\displaystyle t(n-1)} . Следовательно, при превышении значения статистики по абсолютной величине критического значения данного распределения (при заданном уровне значимости) нулевая гипотеза отвергается.
Двухвыборочный t-критерий для независимых выборок
Пусть имеются две независимые выборки объемами n 1 , n 2 {\displaystyle n_{1}~,~n_{2}} нормально распределенных случайных величин X 1 , X 2 {\displaystyle X_{1},~X_{2}} . Необходимо проверить по выборочным данным нулевую гипотезу равенства математических ожиданий этих случайных величин H 0 : M 1 = M 2 {\displaystyle H_{0}:~M_{1}=M_{2}} .
Рассмотрим разность выборочных средних Δ = X ¯ 1 − X ¯ 2 {\displaystyle \Delta ={\overline {X}}_{1}-{\overline {X}}_{2}} . Очевидно, если нулевая гипотеза выполнена E ( Δ ) = M 1 − M 2 = 0 {\displaystyle E(\Delta )=M_{1}-M_{2}=0} . Дисперсия этой разности равна исходя из независимости выборок: V ( Δ ) = σ 1 2 n 1 + σ 2 2 n 2 {\displaystyle V(\Delta )={\frac {\sigma _{1}^{2}}{n_{1}}}+{\frac {\sigma _{2}^{2}}{n_{2}}}} . Тогда используя несмещенную оценку дисперсии s 2 = ∑ t = 1 n ( X t − X ¯ ) 2 n − 1 {\displaystyle s^{2}={\frac {\sum _{t=1}^{n}(X_{t}-{\overline {X}})^{2}}{n-1}}} получаем несмещенную оценку дисперсии разности выборочных средних: s Δ 2 = s 1 2 n 1 + s 2 2 n 2 {\displaystyle s_{\Delta }^{2}={\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}} . Следовательно, t-статистика для проверки нулевой гипотезы равна
t = X ¯ 1 − X ¯ 2 s 1 2 n 1 + s 2 2 n 2 {\displaystyle t={\frac {{\overline {X}}_{1}-{\overline {X}}_{2}}{\sqrt {{\frac {s_{1}^{2}}{n_{1}}}+{\frac {s_{2}^{2}}{n_{2}}}}}}}Эта статистика при справедливости нулевой гипотезы имеет распределение t ( d f ) {\displaystyle t(df)} , где d f = ( s 1 2 / n 1 + s 2 2 / n 2 ) 2 ( s 1 2 / n 1 ) 2 / ( n 1 − 1 ) + ( s 2 2 / n 2 ) 2 / ( n 2 − 1 ) {\displaystyle df={\frac {(s_{1}^{2}/n_{1}+s_{2}^{2}/n_{2})^{2}}{(s_{1}^{2}/n_{1})^{2}/(n_{1}-1)+(s_{2}^{2}/n_{2})^{2}/(n_{2}-1)}}}
Случай одинаковой дисперсии
В случае, если дисперсии выборок предполагаются одинаковыми, то
V ( Δ ) = σ 2 ( 1 n 1 + 1 n 2 ) {\displaystyle V(\Delta )=\sigma ^{2}\left({\frac {1}{n_{1}}}+{\frac {1}{n_{2}}}\right)}Тогда t-статистика равна:
t = X ¯ 1 − X ¯ 2 s X 1 n 1 + 1 n 2 , s X = ( n 1 − 1 ) s 1 2 + ( n 2 − 1 ) s 2 2 n 1 + n 2 − 2 {\displaystyle t={\frac {{\overline {X}}_{1}-{\overline {X}}_{2}}{s_{X}{\sqrt {{\frac {1}{n_{1}}}+{\frac {1}{n_{2}}}}}}}~,~~s_{X}={\sqrt {\frac {(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{n_{1}+n_{2}-2}}}}Эта статистика имеет распределение t ( n 1 + n 2 − 2 ) {\displaystyle t(n_{1}+n_{2}-2)}
Двухвыборочный t-критерий для зависимых выборок
Для вычисления эмпирического значения t {\displaystyle t} -критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:
t = M d s d / n {\displaystyle t={\frac {M_{d}}{s_{d}/{\sqrt {n}}}}}где M d {\displaystyle M_{d}} — средняя разность значений, s d {\displaystyle s_{d}} — стандартное отклонение разностей, а n — количество наблюдений
Эта статистика имеет распределение t ( n − 1 ) {\displaystyle t(n-1)} .
Проверка линейного ограничения на параметры линейной регрессии
С помощью t-теста можно также проверить произвольное (одно) линейное ограничение на параметры линейной регрессии, оцененной обычным методом наименьших квадратов. Пусть необходимо проверить гипотезу H 0 : c T b = a {\displaystyle H_{0}:c^{T}b=a} . Очевидно, при выполнении нулевой гипотезы E ( c T b ^ − a ) = c T E ( b ^ ) − a = 0 {\displaystyle E(c^{T}{\hat {b}}-a)=c^{T}E({\hat {b}})-a=0} . Здесь использовано свойство несмещенности МНК-оценок параметров модели E ( b ^ ) = b {\displaystyle E({\hat {b}})=b} . Кроме того, V ( c T b ^ − a ) = c T V ( b ^ ) c = σ 2 c T ( X T X ) − 1 c {\displaystyle V(c^{T}{\hat {b}}-a)=c^{T}V({\hat {b}})c=\sigma ^{2}c^{T}(X^{T}X)^{-1}c} . Используя вместо неизвестной дисперсии её несмещенную оценку s 2 = E S S / ( n − k ) {\displaystyle s^{2}=ESS/(n-k)} получаем следующую t-статистику:
t = c T b ^ − a s c T ( X T X ) − 1 c {\displaystyle t={\frac {c^{T}{\hat {b}}-a}{s{\sqrt {c^{T}(X^{T}X)^{-1}c}}}}}Эта статистика при выполнении нулевой гипотезы имеет распределение t ( n − k ) {\displaystyle t(n-k)} , поэтому если значение статистики выше критического, то нулевая гипотеза о линейном ограничении отклоняется.
Проверка гипотез о коэффициенте линейной регрессии
Частным случаем линейного ограничения является проверка гипотезы о равенстве коэффициента b j {\displaystyle b_{j}} регрессии некоторому значению a {\displaystyle a} . В этом случае соответстующая t-статистика равна:
t = b ^ j − a s b ^ j {\displaystyle t={\frac {{\hat {b}}_{j}-a}{s_{{\hat {b}}_{j}}}}}где s b ^ j {\displaystyle s_{{\hat {b}}_{j}}} — стандартная ошибка оценки коэффициента — квадратный корень из соответствующего диагонального элемента ковариационной матрицы оценок коэффициентов.
При справедливости нулевой гипотезы распределение этой статистики — t ( n − k ) {\displaystyle t(n-k)} . Если значение статистики по абсолютной величине выше критического значения, то отличие коэффициента от a {\displaystyle a} является статистически значимым (неслучайным), в противном случае — незначимым (случайным, то есть истинный коэффициент вероятно равен или очень близок к предполагаемому значению a {\displaystyle a} )
Замечание
Одновыборочный тест для математических ожиданий можно свести к проверке линейного ограничения на параметры линейной регрессии. В одновыборочном тесте это «регрессия» на константу. Поэтому s 2 {\displaystyle s^{2}} регрессии это и есть выборочная оценка дисперсии изучаемой случайной величины, матрица X T X {\displaystyle X^{T}X} равна n {\displaystyle n} , а оценка «коэффициента» модели равна выборочному среднему. Отсюда и получаем выражение для t-статистики, приведенное выше для общего случая.
Аналогично можно показать, что двухвыборочный тест при равенстве дисперсий выборок также сводится к проверке линейных ограничений. В двухвыборочном тесте это «регрессия» на константу и фиктивную переменную, идентифицирующую подвыборку в зависимости от значения (0 или 1): y = a + b D {\displaystyle y=a+bD} . Гипотеза о равенстве математических ожиданий выборок может быть сформулирована как гипотеза о равенстве коэффициента b этой модели нулю. Можно показать, что соответствующая t-статистика для проверки этой гипотезы равна t-статистике, приведенной для двухвыборочного теста.
Также к проверке линейного ограничения можно свести и в случае разных дисперсий. В этом случае дисперсия ошибок модели принимает два значения. Исходя из этого можно также получить t-статистику, аналогичную приведенной для двухвыборочного теста.
Непараметрические аналоги
Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна — Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков и T-критерий Вилкоксона
Литература
Student. The probable error of a mean. // Biometrika. 1908. № 6 (1). P. 1-25.
Ссылки
О критериях проверки гипотез об однородности средних на сайте Новосибирского государственного технического университета
ru.wikipedia.org
Читайте также
![Таблица критических значений пирсона Таблица критических значений пирсона]() Таблица критических значений пирсона
Таблица критических значений пирсона- Разряды наречий по значению таблица с примерами
![Таблица значений функции Таблица значений функции]() Таблица значений функции
Таблица значений функции![Таблица критических значений спирмена Таблица критических значений спирмена]() Таблица критических значений спирмена
Таблица критических значений спирмена![Таблица критических значений манна уитни Таблица критических значений манна уитни]() Таблица критических значений манна уитни
Таблица критических значений манна уитни![Таблица значений интегральной функции лапласа Таблица значений интегральной функции лапласа]() Таблица значений интегральной функции лапласа
Таблица значений интегральной функции лапласа![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского- 7 Треф значение
![Славянские имена мальчиков и их значение Славянские имена мальчиков и их значение]() Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия![Амбициозный значение слова Амбициозный значение слова]() Амбициозный значение слова
Амбициозный значение слова
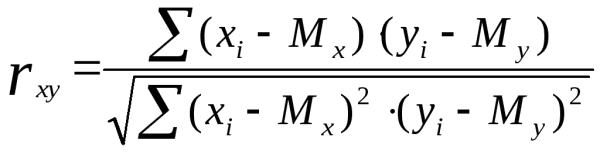 Таблица критических значений пирсона
Таблица критических значений пирсона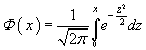 Таблица значений функции
Таблица значений функции Таблица критических значений спирмена
Таблица критических значений спирмена Таблица критических значений манна уитни
Таблица критических значений манна уитни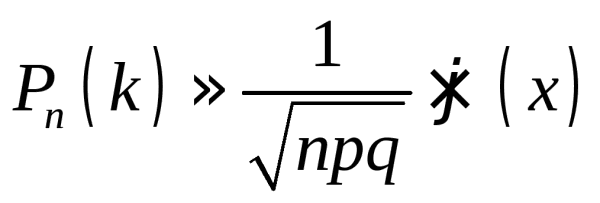 Таблица значений интегральной функции лапласа
Таблица значений интегральной функции лапласа Аутентичность значение слова
Аутентичность значение слова Чувак значение слова с еврейского
Чувак значение слова с еврейского Славянские имена мальчиков и их значение
Славянские имена мальчиков и их значение Барыга значение слова википедия
Барыга значение слова википедия Амбициозный значение слова
Амбициозный значение слова