/ Физика
1.Определение колебательного движения
Колебательное движение - это движение, точно или приблизительно повторяющееся через одинаковые промежутки времени. Учение о колебательном движении в физике выделяют особо. Это обусловлено общностью закономерностей колебательного движения различной природы и методов его исследования. Механические, акустические, электромагнитные колебания и волны рассматриваются с единой точки зрения. Колебательное движение свойственно всем явлениям природы. Внутри любого живого организма непрерывно происходят ритмично повторяющиеся процессы, например биение сердца.
Механические колебанияКолебания - это любой физический процесс, характеризующийся повторяемостью во времени.
Волнение моря, качание маятника часов, вибрации корпуса корабля, биение человеческого сердца, звук, радиоволны, свет, переменные токи — все это колебания.
В процессе колебаний значения физических величин, определяющих состояние системы, через равные или неравные промежутки времени повторяются. Колебания называются периодическими, если значения изменяющихся физических величин повторяются через равные промежутки времени.
Наименьший промежуток времени Т, черезкоторый значение изменяющейся физической величины повторяется (по величине и направлению, если эта величина векторная, по величине и знаку, если она скалярная), называетсяпериодом колебаний.
Число полных колебаний n , совершаемых за единицу времени, называется частотой колебаний этой величины и обозначается через ν . Период и частота колебаний связаны соотношением : ![]()
Любое колебание обусловлено тем или иным воздействием на колеблющуюся систему. В зависимости от характера воздействия, вызывающего колебания, различают следующие виды периодических колебаний: свободные, вынужденные, автоколебания, параметрические.
Свободные колебания — это колебания, происходящие в системе, предоставленной самой себе, после выведения ее из состояния устойчивого равновесия (например, колебания груза на пружине).
Вынужденные колебания — это колебания, обусловленные внешним периодическим воздействием (например, электромагнитные колебания в антенне телевизора).
Механические колебания
Автоколебания — свободные колебания, поддерживаемые внешним источником энергии, включение которого в нужные моменты времени осуществляет сама колеблющаяся система (например, колебания маятника часов).
Параметрические колебания — это колебания, в процессе которых происходит периодическое изменение какого-либо параметра системы (например, раскачивание качелей: приседая в крайних положениях и выпрямляясь в среднем положении, человек, находящийся на качелях, изменяет момент инерции качелей).
Различные по своей природе колебания обнаруживают много общего: они подчиняются одним и тем же закономерностям, описываются одними и теми же уравнениями, исследуются одними и теми же методами. Это дает возможность создать единую теорию колебаний.
Простейшими из периодических колебаний
являются гармонические колебания.
Гармонические колебания- это колебания, в процессе совершения которых значения физических величин изменяются с течением времени по закону синуса или косинуса. Большинство колебательных процессов описываются этим законом или может быть приставлено в виде суммы гармонических колебаний.
Возможно и другое «динамическое» определение гармонических колебании как процесса, совершаемого под действием упругой или «квазиупругой»
силы.
2. Периодическими называются колебания, при которых происходит точное повторение процесса через равные промежутки времени.
Периодом периодических колебаний называется минимальное время, через которое система возвращается в первоначальное
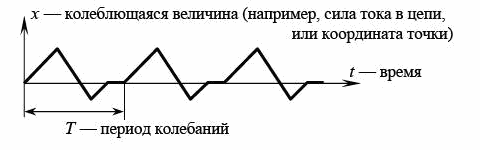
х — колеблющаяся величина (например, сила тока в цепи, состояние и начинается повторение процесса. Процесс, происходящий за один период колебаний, называется «одно полное колебание».
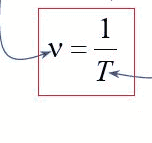
периодических колебаний называется число полных колебаний за единицу времени (1 секунду) — это может быть не целое число.
Т — период колебаний Период — время одного полного колебания.
Чтобы вычислить частоту v, надо разделить 1 секунду на время Т одного колебания (в секундах) и получится число колебаний за 1 секунду или координата точки) t — время
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
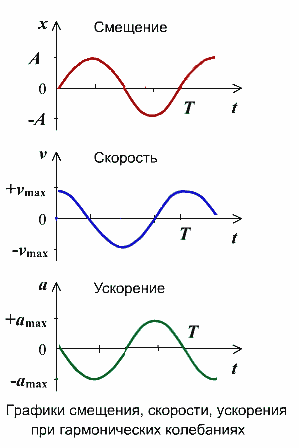
График гармонического колебания
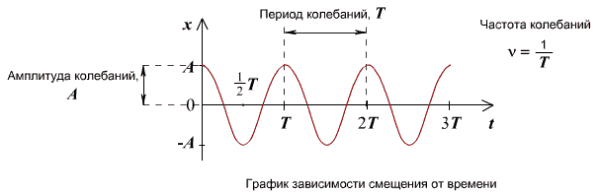
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
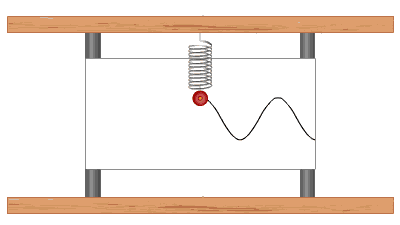
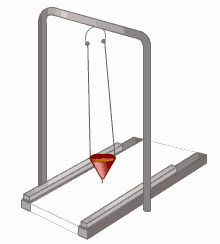
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
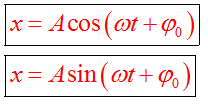
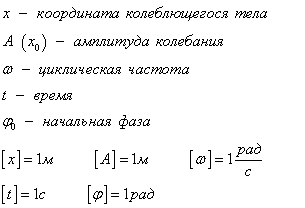
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой ![]() .
.
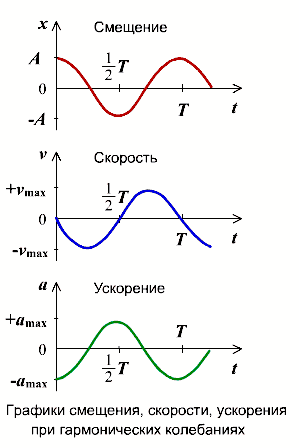
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, каксила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия - достигает максимального значения.
Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса
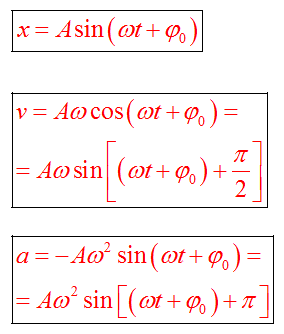
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
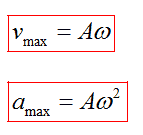

Как получить зависимости v(t) и a(t)
StudFiles.ru
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ
Колебательными называются процессы, при которых параметры, характеризующие состояние колебательной системы, обладают определённой повторяемостью во времени. Такими процессами, например, могут являться суточные и годовые колебания температуры атмосферы и поверхности Земли, колебания маятников и т.д.
Если промежутки времени, через которые состояние системы повторяется, равны между собой, то колебания называются периодическими, а промежуток времени между двумя последовательными одинаковыми состояниями системы – периодом колебаний.
Для периодических колебаний функция, определяющая состояние колеблющейся системы, повторяется через период колебаний:
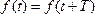
Среди периодических колебаний особое место занимают колебания гармонические, т.е. колебания, при которых характеристики движения системы изменяются по гармоническому закону, например:
 (308)
(308)
Наибольшее внимание, уделяемое в теории колебаний именно часто встречающимся на практике гармоническим процессам, объясняется как тем, что для них наиболее хорошо развит аналитический аппарат, так и тем, что любые периодические колебания (и не только периодические) могут быть рассмотрены в виде определённой комбинации гармонических составляющих. В силу этих причин далее будут рассмотрены преимущественно гармонические колебания. В аналитическом выражении гармонических колебаний (308) величина x отклонения материальной точки от положения равновесия называется смещением.
Очевидно, что максимальное отклонение точки от положения равновесия равно a, эта величина называется амплитудой колебаний. Физическая величина, равная:
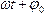
и определяющая состояние колеблющейся системы в данный момент времени, называется фазой колебаний. Значение фазы в момент начала от счёта времени

называется начальной фазой колебаний. Величина w в выражении фазы колебаний, определяющая быстроту колебательного процесса, называется его круговой или циклической частотой колебаний.
Состояние движения при периодических колебаниях должно повторяться через промежутки времени, равные периоду колебаний T. При этом, очевидно, фаза колебаний должна изменятся на 2p (период гармонической функции), т.е.:

Отсюда следует, что период колебаний и циклическая частота связаны между собой соотношением:
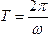
Скорость точки, закон движения которой определяется (301), также изменяется по гармоническому закону
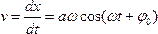 (309)
(309)
Отметим, что смещение и скорость точки неодновременно обращаются в нуль или принимают максимальные значения, т.е. смешение и скорость отличаются по фазе.
Аналогично получаем, что ускорение точки равно:
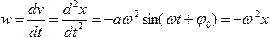 (310)
(310)
Из выражения для ускорения видно, что оно смещено по фазе относительно смещения и скорости. Хотя смешение и ускорение одновременно проходят через нуль, в этот момент времени они имеют противоположные направления, т.е. смещены на p. Графики зависимостей смещения, скорости и ускорения от времени при гармонических колебаниях представлены условном масштабе на рис.81.
|
|

Циклическая частота колебаний и период определяются внутренними параметрами системы, а амплитуда колебаний и начальная фаза - начальными условиями; при этом под начальными условиями понимают значения смещения, и скорости материальной точки в момент начала отсчёта времени:
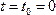
Из закона гармонического движения (308), пользуясь формулами тригонометрических преобразований, можно записать:
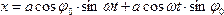
Обозначив 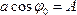 и
и 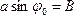 выражение закона движения можно представить в виде
выражение закона движения можно представить в виде
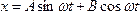 (311)
(311)
Выражение (311) показывает, что гармоническое колебание с произвольной начальной фазой, отличной от нуля, можно представить в виде суммы двух гармонических колебаний с нулевыми начальными фазами, происходящих по законам синуса и косинуса, при соответствующем подборе амплитуд составляющих.
Начальные условия, как было отмечено выше, определяются значениями смещения и скорости в момент начала отсчёта времени
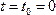
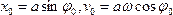 (312)
(312)
Из начальных условий, представленных в виде (312), легко определяются значения амплитуды и начальной фазы колебаний:
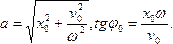 (313)
(313)
Пояснить влияние начальных условий на характер последующих колебаний системы можно на двух простых частных примерах. В первом случае будем полагать, что в начальный момент времени тело (например, тело маятника) вывели из положения равновесия, сообщив ему отклонение А, и без толчка отпустили. Начальные условия для такого случая имеют вид:

Подставив значения начальных смещения и скорости в (313), получим:

Таким образом, при заданных начальных условиях колебания тела будут происходить без начальной фазы по закону косинуса с амплитудой, равной начальному отклонению тела от положения равновесия.
Если же, во втором случае, в исходный момент времени телу в положении равновесия (начальное отклонение отсутствует) толчком сообщили скорость, то начальные значения смещения и скорости равны 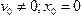 . Подставив эти значения в (313) получаем:
. Подставив эти значения в (313) получаем:
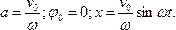
Следовательно, и в этом случае колебания происходят без начальной фазы (начальная фаза равна нулю), но на этот раз по закону синуса с амплитудой, равной 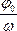 .
.
Важными характеристиками колебательного движения являются их форма, периодичность и т.д. Эти характеристики, независимо от природы колебаний, присущи как колебаниям механическим, так и электрическим, тепловым. Что же касается причин, вызывающих и обусловливающих колебания, то они определяются природой колебательной системы. Далее будем рассматривать механические колебательные системы, например, колебания системы при выводе её из положения равновесия при наличии внутренних упругих взаимодействий. Такие колебания системы, выведенной из положения равновесия, я затем предоставленной самой себе, называются свободными. Характер свободных колебаний зависит от того, насколько большим будет сопротивление движению. Если таковым можно пренебречь, то колебания можно считать чисто гармоническими, с неизменной амплитудой, а при наличии трения амплитуда колебаний будет с течением времени уменьшаться по определённому закону, и колебания нельзя представить только гармонической функцией. В первом случае колебания обычно называют собственными, во втором - затухающими.
studopedia.ru
Основные определения колебательного движения
Изучение данных вопросов необходимо для изучения колебательных движений механической системы в дисциплине «Детали машин», для решения задач в дисциплинах «Теория машин и механизмов» и «Сопротивление материалов».
Лекция 10. Исследование колебаний механических систем.
В данной лекции рассматриваются следующие вопросы:
1. Основные определения колебательного движения.
2. Малые свободные колебания системы.
3. Свободные колебания системы с учетом сил сопротивления движению.
4. Вынужденные колебания системы.
5. Влияние сопротивления на вынужденные колебания.
Колебательным движением материальной системы называется такое ее движение, при котором она через некоторые промежутки времени постоянно возвращается к определенному положению.
Нетрудно обнаружить, что большинство окружающих нас систем совершают колебательное движение.
Если время, за которое все точки системы возвращаются к любому определенному положению с равными скоростями, постоянно и одинаково, то такое время Т называется периодом колебаний. А эти колебания – периодическим колебательным движением.
На рис.79 показан пример изменения какой-то обобщенной координаты q при довольно сложном колебательном процессе. А на рис.80 – при более организованных, периодических колебаниях.
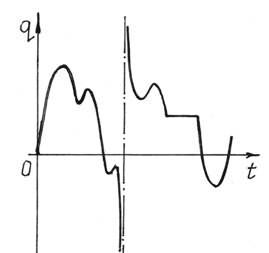
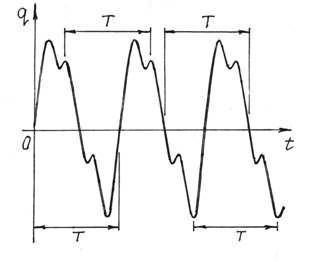
studopedia.ru
Дайте определение механическое колебание - это...?
Лилюша
Механические колебания – это повторяющееся движение, при котором тело многократно проходит одно и то же положение в пространстве. Различают периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени.
Примерами механических колебаний могут служить движение шара на пружине, на нити, движение ножек звучащего камертона или молекул воздуха вблизи него . В физике рассматривают и другие колебания – процессы, обладающие той или иной степенью повторяемости во времени (например, электромагнитные колебания. )
Колебания можно классифицировать по условиям возникновения (свободные, вынужденные, автоколебания) и по характеру изменения во времени кинематических характеристик (пилообразные, гармонические, затухающие).
Ольга г
повторяющийся в той или иной степени во времени процесс изменения состояний системы. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Ирина андрианова
Механические КолебаL9;ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Читайте также
![Дайте определение понятию авария Дайте определение понятию авария]() Дайте определение понятию авария
Дайте определение понятию авария![Данные это в информатике определение Данные это в информатике определение]() Данные это в информатике определение
Данные это в информатике определение![Дайте определение социологии Дайте определение социологии]() Дайте определение социологии
Дайте определение социологии![Дать определение синонимов и антонимов Дать определение синонимов и антонимов]() Дать определение синонимов и антонимов
Дать определение синонимов и антонимов- Дать определение понятию индустриализация
- Дать определение
![Равномерное прямолинейное движение определение Равномерное прямолинейное движение определение]() Равномерное прямолинейное движение определение
Равномерное прямолинейное движение определение![Определение частоты дыхательных движений Определение частоты дыхательных движений]() Определение частоты дыхательных движений
Определение частоты дыхательных движений![Дайте определение термину отказ Дайте определение термину отказ]() Дайте определение термину отказ
Дайте определение термину отказ![Определение чрезвычайной ситуации дано в федеральном законе Определение чрезвычайной ситуации дано в федеральном законе]() Определение чрезвычайной ситуации дано в федеральном законе
Определение чрезвычайной ситуации дано в федеральном законе![Дайте определение понятию управление Дайте определение понятию управление]() Дайте определение понятию управление
Дайте определение понятию управление![Официальное определение государственной тайны дано Официальное определение государственной тайны дано]() Официальное определение государственной тайны дано
Официальное определение государственной тайны дано
 Дайте определение понятию авария
Дайте определение понятию авария Данные это в информатике определение
Данные это в информатике определение Дайте определение социологии
Дайте определение социологии Дать определение синонимов и антонимов
Дать определение синонимов и антонимов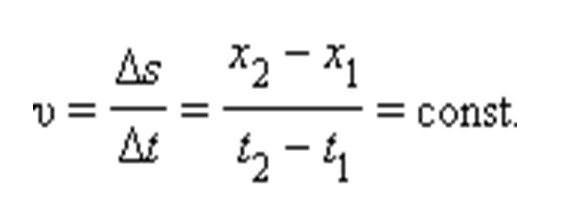 Равномерное прямолинейное движение определение
Равномерное прямолинейное движение определение Определение частоты дыхательных движений
Определение частоты дыхательных движений Дайте определение термину отказ
Дайте определение термину отказ Определение чрезвычайной ситуации дано в федеральном законе
Определение чрезвычайной ситуации дано в федеральном законе Дайте определение понятию управление
Дайте определение понятию управление Официальное определение государственной тайны дано
Официальное определение государственной тайны дано