Множество
У этого термина существуют и другие значения, см. Множество (значения).Мно́жество — одно из ключевых понятий математики, в частности, теории множеств и логики.
Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть несводимое к другим понятиям, а значит, и не имеющее определения; для его объяснения используются описательные формулировки, характеризующие множество как совокупность различных элементов, мыслимое как единое целое[1][2]. Также возможно косвенное определение через аксиомы теории множеств. Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством.
История понятия
Основная статья: История теории множествОсновы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов.
С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты назвал элементами множества. Множество объектов, обладающих свойством A ( x ) {\displaystyle A(x)} , обозначил { x ∣ A ( x ) } {\displaystyle \{x\mid A(x)\}} . Если некоторое множество Y = { x ∣ A ( x ) } {\displaystyle Y=\{x\mid A(x)\}} , то A ( x ) {\displaystyle A(x)} назвал характеристическим свойством множества Y {\displaystyle Y} .
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств, а вновь построенную — аксиоматической теорией множеств.
В практике, сложившейся с середины XX века множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Элемент множества
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если a {\displaystyle a} — элемент множества A {\displaystyle A} , то записывают a ∈ A {\displaystyle a\in A} (« a {\displaystyle a} принадлежит A {\displaystyle A} »). Если a {\displaystyle a} не является элементом множества A {\displaystyle A} , то записывают a ∉ A {\displaystyle a\notin A} (« a {\displaystyle a} не принадлежит A {\displaystyle A} »). В отличие от мультимножества каждый элемент множества уникален, и во множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его:
{ 6 , 11 } = { 11 , 6 } = { 11 , 11 , 6 , 11 , 6 } {\displaystyle \{6,11\}=\{11,6\}=\{11,11,6,11,6\}} .Некоторые виды множеств и сходных объектов
Специальные множества
- Пустое множество — множество, не содержащее ни одного элемента.
- Универсальное множество (универсум) — множество, содержащее все мыслимые объекты. В связи с парадоксом Рассела данное понятие трактуется в настоящее время как «множество, включающее все множества, участвующие в рассматриваемой задаче».
- Частично упорядоченное множество, вполне упорядоченное множество — множество, на котором задано отношение порядка.
Сходные объекты
- Кортеж (в частности, упорядоченная пара) — упорядоченная совокупность конечного числа именованных объектов. Записывается внутри круглых или угловых скобок, а элементы могут повторяться.
- Мультимножество (в теории сетей Петри называется «комплект») — множество с кратными элементами.
- Пространство — множество с некоторой дополнительной структурой.
- Вектор — элемент линейного пространства, содержащий конечное число элементов некоторого поля в качестве координат. Порядок имеет значение, элементы могут повторяться.
- Последовательность — функция одного натурального переменного. Представляется как бесконечный набор элементов (не обязательно различных), порядок которых имеет значение.
- Нечёткое множество — математический объект, подобный множеству, принадлежность которому задаётся не отношением, а функцией. Иными словами, относительно элементов нечёткого множества можно говорить «в какой мере» они в него входят, а не просто, входят они в него или нет.
По иерархии
- Множество множеств (в частности, булеан — множество всех подмножеств данного множества).
- Подмножество
- Надмножество
Отношения между множествами
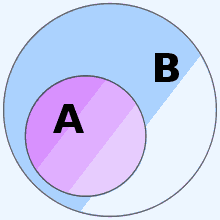 Диаграмма Эйлера для A ⊂ B {\displaystyle A\subset B} Основная статья: Подмножество
Диаграмма Эйлера для A ⊂ B {\displaystyle A\subset B} Основная статья: Подмножество
Два множества A {\displaystyle A} и B {\displaystyle B} могут вступать друг с другом в различные отношения.
- A {\displaystyle A} включено в B {\displaystyle B} , если каждый элемент множества A {\displaystyle A} принадлежит также и множеству B {\displaystyle B} : A ⊆ B ⇔ ∀ a ∈ A : a ∈ B {\displaystyle A\subseteq B\Leftrightarrow \forall a\in A\colon a\in B}
- A {\displaystyle A} включает B {\displaystyle B} , если B {\displaystyle B} включено в A {\displaystyle A} : A ⊇ B ⇔ B ⊆ A {\displaystyle A\supseteq B\Leftrightarrow B\subseteq A}
- A {\displaystyle A} равно B {\displaystyle B} , если A {\displaystyle A} и B {\displaystyle B} включены друг в друга: A = B ⇔ ( A ⊆ B ) ∧ ( B ⊆ A ) {\displaystyle A=B\Leftrightarrow (A\subseteq B)\land (B\subseteq A)}
- A {\displaystyle A} строго включено в B {\displaystyle B} , если A {\displaystyle A} включено в B {\displaystyle B} , но не равно ему: A ⊂ B ⇔ ( A ⊆ B ) ∧ ( A ≠ B ) {\displaystyle A\subset B\Leftrightarrow (A\subseteq B)\land (A\neq B)}
- A {\displaystyle A} строго включает B {\displaystyle B} , если B {\displaystyle B} строго включено в A {\displaystyle A} : A ⊃ B ⇔ B ⊂ A {\displaystyle A\supset B\Leftrightarrow B\subset A}
- A {\displaystyle A} и B {\displaystyle B} не пересекаются, если у них нет общих элементов: A {\displaystyle A} и B {\displaystyle B} не пересекаются ⇔ ∀ a ∈ A : a ∉ B {\displaystyle \Leftrightarrow \forall a\in A\colon a\notin B}
- A {\displaystyle A} и B {\displaystyle B} находятся в общем положении, если существует элемент, принадлежащий исключительно множеству A {\displaystyle A} , элемент, принадлежащий исключительно множеству B {\displaystyle B} , а также элемент, принадлежащий обоим множествам: A {\displaystyle A} и B {\displaystyle B} находятся в общем положении ⇔ {\displaystyle \Leftrightarrow } ∃ a , b , c : ( a ∈ A ) ∧ ( a ∉ B ) ∧ ( b ∈ B ) ∧ ( b ∉ A ) ∧ ( c ∈ A ) ∧ ( c ∈ B ) {\displaystyle \exists a,b,c\colon (a\in A)\land (a\notin B)\land (b\in B)\land (b\notin A)\land (c\in A)\land (c\in B)}
Операции над множествами
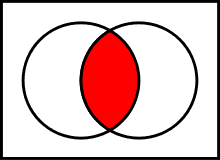 Диаграмма Венна для A ∩ B {\displaystyle A\cap B}
Диаграмма Венна для A ∩ B {\displaystyle A\cap B} 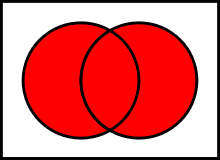 Диаграмма Венна для A ∪ B {\displaystyle A\cup B}
Диаграмма Венна для A ∪ B {\displaystyle A\cup B} 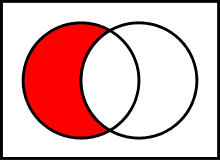 Диаграмма Венна для A ∖ B {\displaystyle A\setminus B}
Диаграмма Венна для A ∖ B {\displaystyle A\setminus B}  Диаграмма Венна для A △ B {\displaystyle A\triangle B}
Диаграмма Венна для A △ B {\displaystyle A\triangle B}
Бинарные операции
Основные бинарные операции, определяемые над множествами:
- пересечение: A ∩ B := { x ∣ x ∈ A ∧ x ∈ B } {\displaystyle A\cap B:=\{x\mid x\in A\land x\in B\}} .
- объединение: A ∪ B := { x ∣ x ∈ A ∨ x ∈ B } {\displaystyle A\cup B:=\{x\mid x\in A\lor x\in B\}} .
- разность: A ∖ B := A ∩ B ¯ = { x ∣ x ∈ A ∧ x ∉ B } {\displaystyle A\setminus B:=A\cap {\overline {B}}=\{x\mid x\in A\land x\notin B\}} .
- симметрическая разность: A △ B ≡ A − ˙ B := {\displaystyle A\triangle B\equiv A{\dot {-}}B:=} ( A ∪ B ) ∖ ( A ∩ B ) = A ∩ B ¯ + A ¯ ∩ B = {\displaystyle (A\cup B)\setminus (A\cap B)=A\cap {\overline {B}}+{\overline {A}}\cap B=} = { x ∣ ( x ∈ A ∧ x ∉ B ) ∨ ( x ∉ A ∧ x ∈ B ) } {\displaystyle =\{x\mid (x\in A\land x\notin B)\lor (x\notin A\land x\in B)\}} .
- декартово или прямое произведение: A × B = { ( a , b ) ∣ a ∈ A , b ∈ B } {\displaystyle A\times B=\{(a,\;b)\mid a\in A,\;b\in B\}} .
Для объяснения смысла операций часто используются диаграммы Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Всякая система множеств, замкнутая относительно операций объединения и пересечения, образует относительно объединения и пересечения дистрибутивную решётку.
Унарные операции
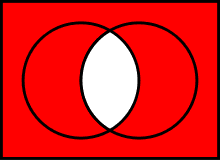 Диаграмма Венна для ( A ∩ B ) ∁ {\displaystyle (A\cap B)^{\complement }}
Диаграмма Венна для ( A ∩ B ) ∁ {\displaystyle (A\cap B)^{\complement }}
Дополнение определяется следующим образом:
A ¯ ≡ A ∁ := { x ∣ x ∉ A } {\displaystyle {\overline {A}}\equiv A^{\complement }:=\{x\mid x\notin A\}} .Операция дополнения подразумевает некоторый зафиксированный универсум (универсальное множество U {\displaystyle U} , которое содержит A {\displaystyle A} ), и сводится к разности множеств с этим универсумом:
A ¯ = U ∖ A {\displaystyle {\overline {A}}=U\setminus A} .Система множеств с фиксированным универсумом, замкнутая относительно операций объединения, пересечения с введённым таким образом дополнением образует булеву алгебру.
Булеан — множество всех подмножеств:
2 X ≡ P X := { A ∣ A ⊂ X } {\displaystyle 2^{X}\equiv {\mathcal {P}}X:=\{A\mid A\subset X\}} .Обозначение 2 X {\displaystyle 2^{X}} происходит из свойства мощности множества всех подмножеств конечного множества:
| 2 X | = 2 | X | {\displaystyle \left|2^{X}\right|=2^X} .Булеан 2 X {\displaystyle 2^{X}} порождает систему множеств с фиксированным универсумом X {\displaystyle X} , замкнутую относительно операций объединения и пересечения, то есть, образует булеву алгебру.
Приоритет операций
Последовательность выполнения операций над множествами, как и обычно, может быть задана скобками. При отсутствии скобок сначала выполняются унарные операции (дополнение), затем — пересечения, затем — объединения и разности, которые имеют одинаковый приоритет. Операции одного приоритета выполняются слева направо. При этом надо иметь ввиду, что в отличии от арифметических сложения и вычитания, для которых верно, что ( a + b ) − c = a + ( b − c ) {\displaystyle (a+b)-c=a+(b-c)} , для аналогичных операций над множествами это неверно. Например, если A = { 1 , 3 } , B = { 1 , 2 } , C = { 2 , 3 } , {\displaystyle A=\{1,3\},B=\{1,2\},C=\{2,3\},} то ( A ∪ B ) ∖ C = { 1 } , {\displaystyle (A\cup B)\setminus C=\{1\},} но, в то же время, A ∪ ( B ∖ C ) = { 1 , 3 } {\displaystyle A\cup (B\setminus C)=\{1,3\}} .
Мощность
Основная статья: Мощность множестваМощность множества — характеристика множества, обобщающая понятие о количестве элементов для конечного множества таким образом, чтобы множества, между которыми возможно установление биекции были равномощны. Обозначается | A | A или ♯ A {\displaystyle \sharp A} . Мощность пустого множества равна нулю, для конечных множеств мощность совпадает с числом элементов, для бесконечных множеств вводятся специальные кардинальные числа, соотносящиеся друг с другом по принципу включения (если A ⊆ B {\displaystyle A\subseteq B} , то | A | ⩽ | B | \leqslant ) и распространением свойства мощности булеана конечного множества: | 2 A | = 2 | A | {\displaystyle |2^{A}|=2^A} на случай бесконечных множеств (само обозначение 2 A {\displaystyle 2^{A}} мотивировано этим свойством).
Наименьшая бесконечная мощность обозначается ℵ 0 {\displaystyle \aleph _{0}} , это мощность счётного множества. Мощность континуума, биективного булеану счётного множества обозначается c {\displaystyle {\mathfrak {c}}} или 2 ℵ 0 {\displaystyle 2^{\aleph _{0}}} . Континуум-гипотеза — предположение о том, что между счётной мощностью и мощностью континуума нет промежуточных мощностей.
ru.wikipedia.org
Тема 1. Множества и операции над ними
Содержание
-
Понятие множества и элемента множества.
-
Способы задания множества.
-
Отношения между множествами. Подмножества.
-
Изображение отношений между множествами при помощи кругов Эйлера.
Основная литература 7, 10, 11, 16, 23, 33, 34;
Дополнительная литература 2, 31, 82, 87, 92
Введение
Успешное обучение математике младших школьников требует от учителя не только мастерства, но и глубокого понимания сути математических понятий и факторов. Дело не только в том, что в начальных классах закладываются основы таких важнейших понятий, как «число» и «величина», происходит ознакомление с элементами буквенной символики и геометрии, развиваются логические умения, но и в том, что многие математические понятия младшие школьники используют без строгих определений, а во многих случаях и неявно. Все это предъявляет особые требования к математической подготовке учителя начальных классов. Он должен владеть понятиями натурального числа и величины, знать различные определения арифметических действий над числами, их свойства, уметь выполнять и объяснять устные и письменные вычисления, обосновывать выбор действия и устанавливать вид зависимости между величинами при решении текстовых задач. Учителю необходимо и умение использовать уроки математики для воспитания учащихся, в частности для формирования у них основ научного мировоззрения.
Математика, как и другие науки изучает окружающий нас мир, природные и общественные явления, но изучает лишь их особые стороны. Например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие их свойства: цвет, массу, твердость. От всего этого отвлекаются, абстрагируются. Поэтому в геометрии вместо слова «предмет» говорят: «Геометрическая фигура».
Результатом абстрагирования являются и такие важнейшие математические понятия, как «число» и «величина».
Вообще, любые математические объекты– это результат выделения из предметов и явлений окружающего мира количественных и пространственных свойств и отношений и абстрагирования их от всех других свойств. Следовательно, математические объекты реально не существуют, нет в окружающем нас мире геометрических фигур, чисел и т.д. Все они созданы человеческим умом в процессе исторического развития общества и существуют лишь в мышлении человека.
Более того, при образовании математических объектов происходит не только абстрагирование от многих свойств предметов, но и приписывание им таких свойств, которыми никакие реальные предметы не обладают. Например, свойство неограниченной протяженности в обоих направлениях – прямой не обладает ни какой реальный предмет.
Эта лекция будет посвящена одному из таких математических объектов - понятию множества.
1. Понятие множества и элемента множества
Множество – одно из основных понятий современной математики, используемое почти во всех ее разделах.
Во многих вопросах приходится рассматривать некоторую совокупность элементов как единое целое. Так, биолог, изучая животный мир и растительный мир данной области, классифицирует все особи по видам, виды по родам. Каждый вид является некоторой совокупность живых существ, рассматриваемой как единое целое.
Для математического описания таких совокупностей и было введено понятие множества. По словам одного из создателей теории множеств – немецкого математика Георга Кантора (1845–1918), «множество есть многое, мыслимое нами как целое». Разумеется, эти слова не могут рассматриваться как математически строгое определение множества, такового определения не существует, поскольку понятие множества является исходным, на основе которого строятся остальные понятия математики. Но из этих слов ясно, что можно говорить о множестве чисел от 1 до 10, натуральных числах, множестве треугольников и квадратов на плоскости.
Понятие множества является одним из основных понятийматематики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве учащихся некоторого класса, о множестве гласных букв русского алфавита, о множестве натуральных чисел.
Математический смысл слова «множество» отличается от того, как оно используется в обычной речи, где его связывают с большим количеством предметов. В математике этого не требуется. Здесь рассматривают множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.
В основном множества обозначают буквами латинского алфавита: A, B, C, …, Z, L.
Определение. Множество, не содержащее ни одного объекта, называют пустым и обозначают знаком .
Определение. Объекты, из которых образовано множество, называют его элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c, …, z.
В математике и других науках нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Например, мы говорим, что число 5 натуральное. Другими словами, число 5 принадлежит множеству натуральных чисел. Или, например, число 0,45 не является натуральным числом. Это означает, что число 0,45 не принадлежит множеству натуральных чисел.
Предложение вида “ Объект а принадлежит множеству А” можно записать, используя символы: аА. Прочитать его можно по-разному:
Объект а принадлежит множеству А.
Объект а – элемент множества А.
Множество А содержит элемент а.
Предложение “ Объект а не принадлежит множеству А” можно записать так: а А. Его читают:
Объект а не принадлежит множеству А.
Объект а не является элементом множества А.
Множество А не содержит элемента а.
Пример
Пусть А – множество однозначных чисел. Тогда предложение “7А” можно прочитать: “Число 7 однозначное”, а запись “ 14 А” означает: “Число 14 не является однозначным”.
Множества бывают конечными и бесконечными. Так, множество дней недели конечно, а множество точек прямой бесконечно. Бесконечными множествами являются и такие множества, как множество натуральных чисел (N), множество целых чисел (Z), множество рациональных чисел (Q), множество действительных чисел (R).
StudFiles.ru
Лекция 1 основные понятия теории множеств Основные определения
Множество – совокупность вполне определённых различимых элементов, рассматриваемых как единое целое.
В зависимости от предмета рассмотрения элементы множества могут быть самой различной природы.
При решении прикладных задач можно говорить о множестве людей, живущих в городе, множестве букв алфавита, множестве учитываемых факторов при оценке обстановки, множестве процессов химического производства, и таких примеров можно привести сколько угодно.
Элементами множества могут быть не только конкретные, но и абстрактные объекты. Например, вполне естественно говорить о множестве вещественных чисел, множестве символов, множестве функций и других объектов теоретических построений, в том числе о множестве возможных решений.
При абстрактном описании множества принято обозначать большими латинскими буквами X, Y, Z, M,…
Элементы множеств обозначаются соответственно малыми буквами x, y, z, m,…
Принадлежность элемента yjмножеству Y символически записывается в виде yj![]() Y, азапись xi
Y, азапись xi![]() Y обозначает, что элемент xiне принадлежит множеству Y.
Y обозначает, что элемент xiне принадлежит множеству Y.
Множества бывают конечными и бесконечными.
Конечное множество содержит вполне определённое число N элементов.
Бесконечное множество содержит бесконечно большое число элементов.
Существует два способа задания множеств – перечисление и описание.
При задании множества перечислением его общим обозначением служит пара фигурных скобок {}, внутри которых перечисляются, обычно через запятые, обозначения элементов множества.
Например, конечное и бесконечное множества соответственно записываются как Y={y1,y2,…,yn} и Z={0, 1, 2,…}.
Для сокращения записи иногда конечное и бесконечное множества, используя индексы, записывают в виде Y={yj}(j=1,…,n) и Z={i} (i=1,2,3…) соответственно.
Описательный способ задания множества состоит в том, что указывается свойство, которым обладают все элементы множества.
Несколько примеров задания множеств методом описания:
1) множествоМ чётных чисел может быть записано в виде М={x│x – чётное число} (что читается так: множество М состоит из элементов x, обладающих тем свойством, что xявляется чётным числом);
2) {x│x2 – 1=0} – множество {+1, –1};
3) если С – множество целых чисел, то {x![]() С│0x
С│0x![]() 7} есть множество {1,2,3,4,5,6,7};
7} есть множество {1,2,3,4,5,6,7};
4) А={x│x – отличник группы} – множество А отличников.
Из определения множества следует, что в нём не должно быть неразличимых (одинаковых) элементов: запись {2, 2, 3, 5} следует рассматривать как некорректную и заменить её на {2, 3, 5}.
устое множество – множество, не содержащее ни одного элемента.
Пустое множество, которое будем условно относить к конечным множествам, обозначается символом ![]() , например, {x
, например, {x![]() С│x2 – x +1=0}=
С│x2 – x +1=0}=![]() .
.
Равные множества – множества, состоящие из одних и тех же элементов.
Равные множества Xи Y представляют собой одно и то же множество Х=Y.
Из определения равенства множеств вытекает, что порядок элементов в множестве несуществен. Так, например, множества {3, 4, 5, 6} и {4, 5, 6, 3} представляют собой одно и то же множество.
Неравные множества Х1![]() Y1, если либо в множестве Xесть элементы, не принадлежащие, либо в множество Y есть элементы, не принадлежащие X.
Y1, если либо в множестве Xесть элементы, не принадлежащие, либо в множество Y есть элементы, не принадлежащие X.
Символ равенства множеств обладает свойствами:
рефлексивность (Х=Х);
симметринностъ (еслиX=Y, то Y=X);
транзитивность (если X=Yи Y=Z, to X=Z)
Подмножество множества Y – множество X, любой элемент которогопринадлежит множеству Y.
Пусть Y – множество студентов группы, aY– множество отличников той же группы. Так как каждый отличник группы является в то же время студентом этой группы, то множество Xявляется подмножеством множества Y.
Универсальное множество – множество, для которого все отличающиеся от него другие рассматриваемые множества являются подмножествами.
Многие определения теории множеств удобно давать в виде математических выражений, содержащих некоторые логические символы. Для определения подмножества используем два таких символа.
![]() –символ, называемый квантором общности, означающий «для всех» (любой, каков бы ни был);
–символ, называемый квантором общности, означающий «для всех» (любой, каков бы ни был);
→ – символ следствия (импликации), означающий «влечет за собой».
Определение подмножества, которое может быть сформулировано в виде: для любого хутверждение «хпринадлежит X» влечет за собой утверждение «х принадлежит Y», запишется так:
StudFiles.ru
Конечное множество
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным. Например,
{ 2 , 4 , 6 , 8 , 10 } {\displaystyle \{2,4,6,8,10\}}конечное множество из пяти элементов. Число элементов конечного множества является натуральным числом и называется мощностью множества. Множество всех положительных целых чисел бесконечно:
{ 1 , 2 , 3 , … } . {\displaystyle \{1,2,3,\ldots \}.}Конечные множества играют особую роль в комбинаторике, которая изучает дискретные объекты. Рассуждения о конечных множествах используют принцип Дирихле, согласно которому не может существовать инъекция из большего конечного множества в меньшее.
Формальное определение
Два множества X {\displaystyle X} и Y {\displaystyle Y} называются эквивалентными, если существует биективное отображение одного множества в другое. Если множества X и Y эквивалентны, то этот факт записывают X ∼ Y {\displaystyle X\sim Y} или | X | = | Y | \displaystyle и говорят, что множества имеют одинаковые мощности.
Множество X {\displaystyle \ X} называется конечным, если оно эквивалентно множеству { 1 , 2 , … , n } {\displaystyle \{1,2,\dots ,n\}} при некотором неотрицательном целом n {\displaystyle \ n} . При этом число n {\displaystyle \ n} называется количеством элементов множества X {\displaystyle \ X} , что записывается как | X | = n =n .[1]
В частности, пустое множество является конечным множеством, количество элементов которого равно 0, то есть, | ∅ | = 0 \varnothing .
Существуют и другие определения конечного множества:
- множество конечно, если оно индуктивно;
- множество конечно, если множество всех его подмножеств нерефлексивно[2];
- множество конечно, если оно нерефлексивно;
- множество конечно, если оно не является объединением двух непересекающихся множеств, каждое из которых эквивалентно данному множеству[2].
Проблема определения конечности множеств в общем случае неразрешима (теорема Трахтенброта). Не существует ни самого слабого, ни самого сильного определения конечного множества. Для каждой логической формулы, являющейся определением конечного множества, существует более сильная и более слабая формулы. Существует неограниченное число логических формул, определяющих конечные множества, и среди них неограниченное множество независимых определений.
Свойства
- Регулярное множество не эквивалентно никакому своему собственному подмножеству;[1]
- Если конечные множества X 1 , … , X n {\displaystyle X_{1},\dots ,X_{n}} попарно не пересекаются (то есть, X i ∩ X j = ∅ {\displaystyle X_{i}\cap X_{j}=\varnothing } ), то | X 1 ∪ X 2 ∪ ⋯ ∪ X n | = | X 1 | + | X 2 | + ⋯ + | X n | {\displaystyle |X_{1}\cup X_{2}\cup \dots \cup X_{n}|=|X_{1}|+|X_{2}|+\dots +|X_{n}|} ;
- Если X 1 , … , X n {\displaystyle X_{1},\dots ,X_{n}} — конечные множества, то | X 1 × X 2 × ⋯ × X n | = | X 1 | × | X 2 | × ⋯ × | X n | {\displaystyle |X_{1}\times X_{2}\times \dots \times X_{n}|=|X_{1}|\times |X_{2}|\times \dots \times |X_{n}|} ;
- Если X {\displaystyle X} — конечное множество, то мощность его булеана равна | 2 X | = 2 | X | . {\displaystyle \ |2^{X}|=2^.}
ru.wikipedia.org
Что такое множество
Olesia
Мно́жество — одно из ключевых понятий математики, в частности, теории множеств и логики.
Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения. Однако, можно дать описание множества, например в формулировке Георга Кантора: под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M).
Другая формулировка принадлежит Бертрану Расселлу: «Множество есть совокупность различных элементов, мыслимая как единое целое» . Также, возможно косвенное определение через аксиомы теории множеств.
В математической логике и дискретной математике часто употребляемый синоним множества — алфавит.
Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Более того, как в наивной, так и в формальной теориях множеств любой объект обычно считается множеством.
Baby love
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т. д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников. Множества обычно обозначают большими буквами: A, B, C, N, ..а элементы этих множеств − аналогичными маленькими буквами: a, b, c, n, ..Существуют стандартные обозначения для некоторых множеств. Например,
− множество целых чисел;
− множество рациональных чисел;
− множество иррациональных чисел;
− множество действительных чисел;
− множество комплексных чисел.
Если элемент a принадлежит множеству A, то пишут: a A.
Читайте также
![Акт определение Акт определение]() Акт определение
Акт определение- Актив определение
![База данных определение База данных определение]() База данных определение
База данных определение![Бетон определение Бетон определение]() Бетон определение
Бетон определение![Власть определение Власть определение]() Власть определение
Власть определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Генетические механизмы определения пола Генетические механизмы определения пола]() Генетические механизмы определения пола
Генетические механизмы определения пола![Газоопасные работы определение Газоопасные работы определение]() Газоопасные работы определение
Газоопасные работы определение![Выберите один из вариантов определения бытия Выберите один из вариантов определения бытия]() Выберите один из вариантов определения бытия
Выберите один из вариантов определения бытия- Выберите один из вариантов определения истины это
![Вихревое электрическое поле определение Вихревое электрическое поле определение]() Вихревое электрическое поле определение
Вихревое электрическое поле определение![Выберите верное определение материи Выберите верное определение материи]() Выберите верное определение материи
Выберите верное определение материи
 Акт определение
Акт определение База данных определение
База данных определение Бетон определение
Бетон определение Власть определение
Власть определение Болезнь определение
Болезнь определение Генетические механизмы определения пола
Генетические механизмы определения пола Газоопасные работы определение
Газоопасные работы определение Выберите один из вариантов определения бытия
Выберите один из вариантов определения бытия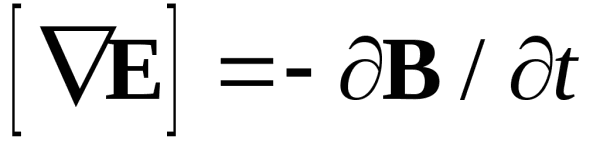 Вихревое электрическое поле определение
Вихревое электрическое поле определение Выберите верное определение материи
Выберите верное определение материи