Способы определения координат центра тяжести.
Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
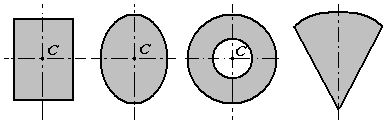
Рис.7
2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.
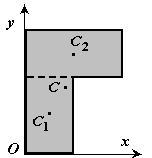
Рис.8
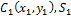
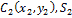
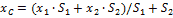
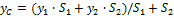
S=S1+S2.
3.Метод отрицательных площадей.Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
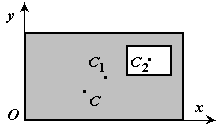
Рис.9
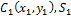
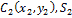
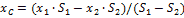
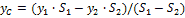
S=S1-S2.
4.Метод группировки.Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы.
Центры тяжести некоторых однородных тел.
1) Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом 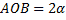 . В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 10).
. В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 10).
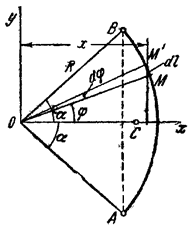
Рис.10
Найдем координату 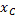 по формуле
по формуле 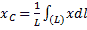 . Для этого выделим на дуге АВ элемент ММ’ длиною
. Для этого выделим на дуге АВ элемент ММ’ длиною  , положение которого определяется углом
, положение которого определяется углом 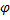 . Координата х элемента ММ’ будет
. Координата х элемента ММ’ будет 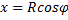 . Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
. Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
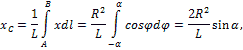
где L - длина дуги АВ, равная  .
.
Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном 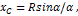
где угол 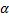 измеряется в радианах.
измеряется в радианах.
2) Центр тяжести площади треугольника. Рассмотрим треугольник, лежащий в плоскости Oxy, координаты вершин которого известны: Ai (xi,yi), (i = 1,2,3). Разбивая треугольник на узкие полоски, параллельные стороне А1А2 , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А3 М3 (рис.11).

Рис.11
Разбивая треугольник на полоски, параллельные стороне А2А3, можно убедиться, что он должен лежать на медиане А1М1. Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.
В частности, для медианы А1М1 получим, учитывая, что координаты точки М1 - это среднее арифметическое координат вершин А2 и А3 :
xc = x1 + (2/3)∙(xМ1 - x1) = x1 + (2/3)∙[(x2 + x3)/2-x1] = (x1+ x2 +x3)/3.
Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:
xc =(1/3)Σxi ; yc =(1/3)Σyi.
3) Центр тяжести площади кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2α, расположенный симметрично относительно оси Ox (рис.12) .
Очевидно, что yc = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле:
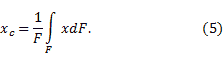
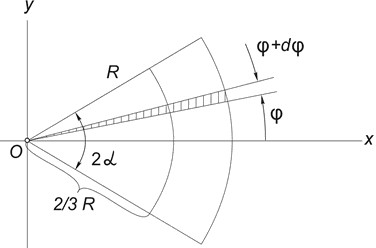
Рис.12
Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом dφ. С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R×dφ и высотой R. Площадь такого треугольника dF=(1/2)R2∙dφ, а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому в (5) положим x = (2/3)R∙cosφ. Подставляя в (5) F = αR2, получим:
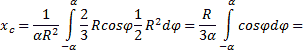
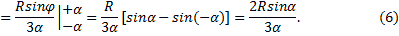
С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга.
Подставляя в (2) α = π/2, получим: xc = (4R)/(3π) ≅ 0,4R . 
Пример 1. Определим центр тяжести однородного тела, изображённого на рис. 13.

Рис.13
Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:
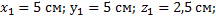
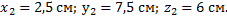
Объёмы их: 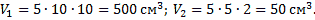
Поэтому координаты центра тяжести тела
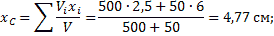
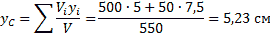
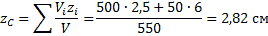
Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.14).

Рис.14
Координаты центров тяжести: 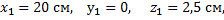
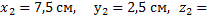 0.
0.
Площади: 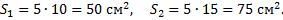
Поэтому:
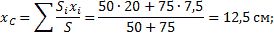
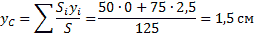
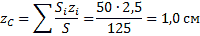
|
 см вырезано квадратное отверстие
см вырезано квадратное отверстие 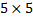 см (рис.15). Найдем центр тяжести листа.
см (рис.15). Найдем центр тяжести листа.
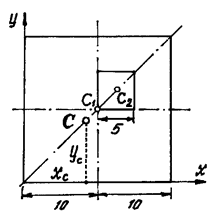
Рис.15
В этой задаче удобнее разделить тело на две части: большой квадрат и квадратное отверстие. Только площадь отверстия надо считать отрицательной. Тогда координаты центра тяжести листа с отверстием:
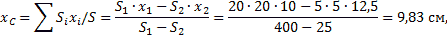
координата  так как тело имеет ось симметрии (диагональ).
так как тело имеет ось симметрии (диагональ).
Пример 4. Проволочная скобка (рис.16) состоит из трёх участков одинаковой длины l.

Рис.16
Координаты центров тяжести участков:
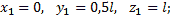
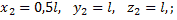
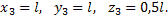
Поэтому координаты центра тяжести всей скобки:
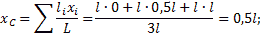

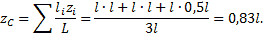
Пример 5. Определить положение центра тяжести фермы, все стержни которой имеют одинаковую погонную плотность (рис.17).
Напомним, что в физике плотность тела ρ и его удельный вес g связаны соотношением: γ= ρg , где g - ускорение свободного падения. Чтобы найти массу такого однородного тела, нужно плотность умножить на его объем.

Рис.17
Термин «линейная» или «погонная» плотность означает, что для определения массы стержня фермы нужно погонную плотность умножить на длину этого стержня.
Для решения задачи можно воспользоваться методом разбиения. Представив заданную ферму в виде суммы 6 отдельных стержней, получим:
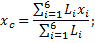
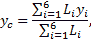
где Li длина i-го стержня фермы, а xi, yi - координаты его центра тяжести.
Решение этой задачи можно упростить, если сгруппировать 5 последних стержней фермы. Нетрудно видеть, что они образуют фигуру, имеющую центр симметрии, расположенный посредине четвертого стержня, где и находится центр тяжести этой группы стержней.
Таким образом, заданную ферму можно представить комбинацией всего двух групп стержней.
Первая группа состоит из первого стержня, для нее L1 = 4 м, x1 = 0 м, y1= 2 м. Вторая группа стержней состоит из пяти стержней, для нее L2 = 20 м, x2= 3 м, y2= 2 м.
Координаты центра тяжести фермы находим по формуле:
xc = (L1∙x1 + L2∙x2)/(L1+ L2) = (4∙0 + 20∙3)/24 = 5/2 м;
yc = (L1∙y1 + L2∙y2)/(L1+ L2) = (4∙2 + 20∙2)/24 = 2 м.
Отметим, что центр С лежит на прямой, соединяющей С1 и С2 и делит отрезок С1С2 в отношении: С1С/СС2 = (xc- x1)/(x2 - xc) = L2 / L1 = 2,5/0,5.
Вопросы для самопроверки
- Что называется центром параллельных сил?
- Как определяются координаты центра параллельных сил?
- Как определить центр параллельных сил, равнодействующая которых равна нулю?
- Каким свойством обладает центр параллельных сил?
- По каким формулам вычисляются координаты центра параллельных сил?
- Что называется центром тяжести тела?
- Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
- Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
- Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?
- Что называют статическим моментом площади?
- Приведите пример тела, центр тяжести которого расположен вне тела.
- Как используются свойства симметрии при определении центров тяжести тел?
- В чем состоит сущность способа отрицательных весов?
- Где расположен центр тяжести дуги окружности?
- Каким графическим построением можно найти центр тяжести треугольника?
- Запишите формулу, определяющую центр тяжести кругового сектора.
- Используя формулы, определяющие центры тяжести треугольника и кругового сектора, выведите аналогичную формулу для кругового сегмента.
- По каким формулам вычисляются координаты центров тяжести однородных тел, плоских фигур и линий?
- Что называется статическим моментом площади плоской фигуры относительно оси, как он вычисляется и какую размерность имеет?
- Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?
- Какими вспомогательными теоремами пользуются при определении положения центра тяжести?
studopedia.ru
Определения положения центра тяжести
К аналитическим методам определения положения центра тяжести относятся метод разбиений и метод отрицательных площадей.
 1. Метод разбиений.Метод заключается в мысленном разбиении тела на несколько простейших (конечных элементов), для которых известно положение центра тяжести. Используют формулы вида (2).
1. Метод разбиений.Метод заключается в мысленном разбиении тела на несколько простейших (конечных элементов), для которых известно положение центра тяжести. Используют формулы вида (2).
2. Метод отрицательных площадей.Заключается в том, что данное тело дополняют до простейшего. При этом дополняющие элементы (их вес, объем, площадь или длину) считают отрицательными.
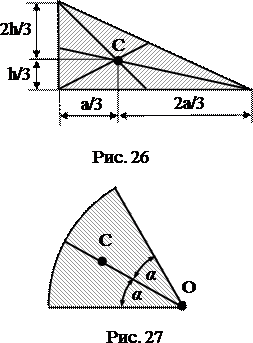
Простейшими являются тела, у которых известно положение центра тяжести (ЦТ). Это: однородные диск и окружность, их ЦТ. находится в центре; прямоугольник и параллелограмм, их ЦТ находится в точке пересечения диагоналей; треугольник, его ЦТ находится в точке пересечения медиан. При этом следует учитывать, что медианы точкой их пересечения делятся в отношении 1:2 (рис. 26). Положение центра тяжести кругового сектора можно определить по формуле: ОС=2/3∙R∙ sinα/α, где α – половина центрального угла, выраженного врадианах (рис. 27). ЦТ тела, имеющего центр, плоскость или ось симметрии находится на них.
Из экспериментальных способов отметим методы взвешивания и подвешивания.
 Метод взвешивания(рис. 28). По известным весу тела P, показаниям весов R и расстоянию a определяют расстояние х из уравнения: ∑mO = - P∙x + R∙a; откуда
Метод взвешивания(рис. 28). По известным весу тела P, показаниям весов R и расстоянию a определяют расстояние х из уравнения: ∑mO = - P∙x + R∙a; откуда
х = R∙a /P.
Метод подвешивания (применяется преимущественно для плоских тел).При этом способе тело подвешивают на нити сначала в одной точке и проводят линию, продолжающую нить, затем в другой точке. Точка пересечения этих линий определит положение ЦТ.
studopedia.ru
11.3. Способы определения координат центров тяжести тел
135
|
n |
|
|
Ус =∑ ℓi . уi / L ; |
(11. 5) |
|
i=1 |
n
Zс =i=1∑ ℓi . zi / L,
где
n
L = ∑ ℓi – длина линейного тела, ℓi – длина отдельной его части.
i=1
Для плоского стержня эти координаты будут определяться:
n
|
Хс =∑ ℓi . хi / L ; |
|
|
i=1 |
|
|
n |
|
|
Ус =∑ ℓi . уi / L ; |
(11. 6) |
|
i=1 |
Для определения координат центров тяжести объемных и плоских тел существуют специальные способы. Рассмотрим наиболее распространенные из них:
1. Способ разделения твердого тела на отдельные части. Для объемного или плоского тела сложной геометрической формы положение центра тяжести можно выразить предварительно разделив его на какое-точисло N простейших тел или фигур, объемы Vi (i = 1, … N), площади Fi и координаты центров тяжести (хi, уi, zi) которых известны. Поэтому координаты центров тяжести сложных объемных тел выразятся:
N
|
Хс =∑ Vi . хi / V ; |
|
|
i=1 |
|
|
N |
|
|
Ус =∑ Vi . уi / V ; |
(11. 7) |
|
i=1 |
N
Zс =∑i=1Vi . zi / V,
для плоских фигур:
136
N
|
Хс =∑ Fi . хi / F ; |
|
|
i=1 |
|
|
N |
|
|
Ус =∑ Fi . уi / F ; |
(11. 8) |
|
i=1 |
При определении координат центров тяжести тел или фигур, содержащих вырезы, не нарушая общности решения, удобно применять способ отрицательных объемов или площадей. Для этого сложное объемное тело или плоскую фигуру рассматривают как единое целое без учета вырезов, с последующим определением объемов или площадей вырезов, как отрицательных величин, вычисляя координаты их центров тяжести. Координаты центров тяжести сложных тел и фигур возможно в этом случае определять по полученным зависимостям (11. 7), (11. 8).
2. Способ интегрирования.
Для объемных или плоских тел, разнообразной формы, содержащих криволинейные очертания граничных поверхностей или контуров, определение координат центров тяжести путем разделения на конечное число простейших тел или фигур не представляется возможным. Поэтому объемное или плоское тело разделяется на множество N малых частей. Полагая, что объемы или площади частей тела стремятся к нулю и переходя к пределу, получим выражения координат центров тяжести для объемных тел сложной формы в виде:
Хс =∫V хdV/V ;
|
Ус =∫V уdV /V; |
(11. 9) |
|
Zс =∫V zdV/V; |
|
|
для плоских фигур: |
|
|
Хс =∫F хdF/F ; |
|
|
Ус =∫F уdF/F ; |
(11. 10) |
|
для линейных тел: |
|
|
Хс =∫L хdℓ/L ; |
|
|
Ус =∫L уdℓ/L ; |
(11. 11) |
|
Zс =∫L zdℓ/L ; |
|
|
для плоской линии или стержня: |
|
|
Хс =∫L хdℓ/L ; |
137
|
Ус =∫L уdℓ/L ; |
(11. 12) |
где dV, dF, dℓ – дифференциалы изменения элементарных объемов, площадей и длин в зависимости от соответствующих координат.
Кроме аналитических способов определения координат центров тяжести существует экспериментальный метод определения рассматриваемых величин
–это способ взвешивания объемных, плоских и линейных тел.
Вчастном случае, когда однородное тело имеет плоскость, ось или центр симметрии, координаты центра тяжести этого тела расположены или в плоскости или на оси, или в центре симметрии, соответственно.
11.4. Координаты центров тяжести основных площадей и линий
Выразим координаты центров тяжести некоторых основных видов плоских фигур и линий (11. 10), (11. 12).
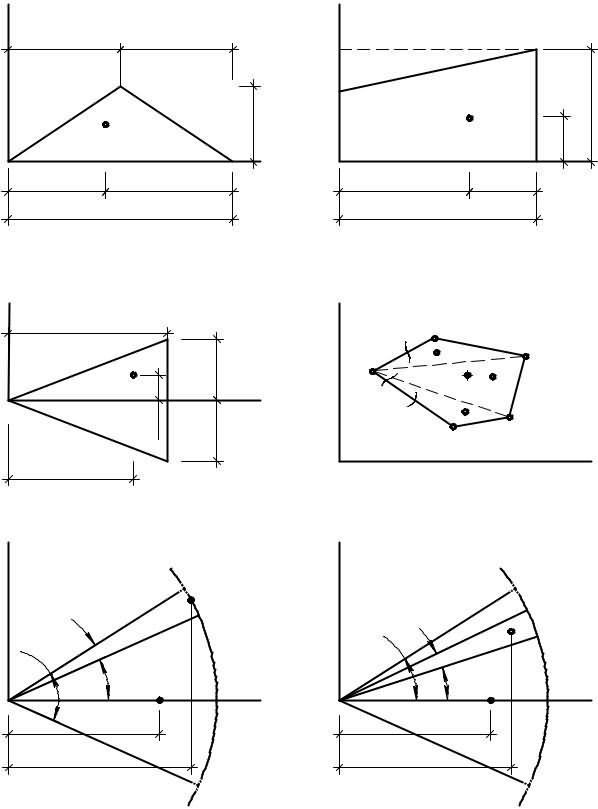
Прямоугольник размерами ℓ . h (рис. 11. 4, а).
|
ℓ |
||
|
F = ∫dF =∫h. dx = ℓ. h ; |
||
|
F |
о |
|
|
ℓ |
||
|
∫x. dx =∫h. xdx = h. ℓ2 / 2 ; |
||
|
F |
о |
|
|
h ℓ2 |
ℓ |
|
|
Хc =----------=----- . |
||
|
2 . ℓ h |
2 |
|
|
Аналогично |
h |
|
|
∫у. dF =∫у. ℓ. dу = ℓ. h2 / 2 ; |
||
|
F |
о |
|
|
ℓ h2 |
h |
|
|
Уc =----------=----- |
||
|
2 . ℓ h |
2 |
|
Прямоугольный треугольник размерами ℓ . h (рис. 11. 4, б).
ℓ
F = ∫dF =∫h / ℓ. хdx = h/ℓ. ℓ2/2 = 1/2 ℓh ;
F о
ℓ
∫x. dF =∫x. h/ℓ. xdx = h / ℓ. ℓ3 / 3 = h ℓ3 / 3ℓ ;
|
F |
о |
|
|
h ℓ3 . 2 |
2 |
|
|
Хc =----------=-----ℓ; |
||
|
3ℓ . ℓ h |
3 |
|
Аналогично вычислим Уc (рис. 11. 4, в).
138
h
F = ∫dF =∫(ℓ - ℓ / h. у)dу = ℓh - ℓ/h. h2/2= 1/2 ℓh ;
F о
h
∫у. dF =∫у. (ℓ - ℓ /hу). dу = ℓ. h2 /2 - ℓ / h. h3 /3 = 1/6 ℓh2 ;
|
F |
о |
|
|
ℓ h2 . 2 |
1 |
|
|
Уc =----------=-----h . |
||
|
6 . ℓ h |
3 |
|
Получили координаты центра тяжести прямоугольного треугольника (рис. 11. 4, г).
Хc = 2/3 ℓ ; Х′c = 1/3 ℓ ; Уc = 1/3 h ; У′c = 2/3 h .
Треугольник с основанием ℓ = а + b, высотой h (рис. 11. 5, а). Его площадь будет складываться из площадей двух прямоугольных треугольников F=1/2аh+ +1/2bh = 1/2ℓh. Вычислим статические моменты двух прямоугольных треугольников относительно осей х, у (11. 4).
2
Sх =i=1∑ Fi . уi = 1/2аh. 1/3h + 1/2bh. 1/3h = 1/6ℓh2 ;
2
Sу =i=1∑ Fi . хi = 1/2аh. 2/3а + 1/2bh. (а + 1/3b) = 1/6ℓh (ℓ + а) ;
и координаты центра тяжести (11. 8):
|
ℓh (ℓ + а) . 2 |
ℓ + а |
|
|
Хc =---------------- |
= --------- |
, |
|
6ℓh |
3 |
|
|
ℓh2 .2 |
||
|
Ус =------------ |
= 1/3h , |
|
|
6ℓh |
||
|
ℓ + а |
ℓ + а |
|
|
Х′c = ℓ -------- |
= ------- |
. |
|
3 |
3 |
|
|
Трапеция с основанием ℓ, высотами h, H (рис. 11.5, б). Воспользуемся |
||
|
способом отрицательных площадей (11. 8). Ее площадь равна: |
||
|
H + h |
||
|
F = ℓ . H – 1/2ℓ (H – h) =--------- |
. ℓ |
|
|
2 |
||
139
а.
y
|
a |
b |
|
С |
h |
||
|
0 |
X'c |
x |
|
|
Xc |
|||
|
l |
в.
|
y |
l |
|
|
С |
h 1 |
|
|
0 |
Yc |
x |
|
2 |
||
|
h |
Xc
д.
y
|
A |
|
|
R |
dl |
| d | |
| f | |
|
2 |
|
| a | |
| j |
С
|
0 |
Xc |
x |
|
X |
||
|
B |
б.
y
|
С |
H |
||
|
h |
Yc |
||
|
0 |
X'c |
x |
|
|
Xc |
|||
|
l |
|
г. |
||||
|
y |
A2 |
(x2 ;y2 ) |
||
|
F1 |
||||
|
A1 (x1 ;y1 ) |
С1 |
A3 (x3 ;y3 ) |
||
|
F2 |
С |
С2 |
||
|
F3 |
С3 |
|||
|
A4 (x4 ;y4 ) |
||||
|
A5 (x5 ;y5 ) |
||||
|
0 |
x |
|||
|
е. |
||||
|
y |
||||
|
A |
||||
| a |
d |
dl |
||
| f | ||||
С
|
0 |
x |
|
|
Xc |
||
|
X |
||
|
R |
B |
Рис. 11.5
140
|
Координаты центра тяжести будут: |
ℓ 2H + h |
|
2 |
|
Хс =∑ Fi . хi / F = [ℓH. ℓ /2 – 1/2ℓ (H – h). 1/3ℓ] / (H + h). ℓ/2 =--- . ---------; |
||
|
i=1 |
3 |
Н + h |
|
ℓ |
H +2h |
|
|
Х′c = ℓ - Хс =-------=----------; |
||
|
3 |
H + h |
|
2
Ус =∑i=1Fi . уi / F = {ℓH. H /2 – 1/2ℓ (H – h). [h + 2/3 (H – h)} / (H + h). ℓ/2 =
1H3 – h3
=----- . -----------; 3 Н2 – h2
Треугольник с основанием h = (h1 + h2) и высотой ℓ (рис. 11. 5, в). Его площадь будет суммироваться из площадей двух прямоугольных треугольников F = 1/2 h1ℓ + 1/2 h2ℓ = 1/2ℓh. Вычислим статические моменты двух треугольников относительно осей х, у.
2
Sх =i=1∑ Fi . уi = 1/2ℓh1 . 1/3h1 + 1/2ℓh2 . (-1/3h2)= 1/6ℓ(h12 – h22);
2
Sу =i=1∑ Fi . хi = 1/2ℓh1 . 2/3ℓ + 1/2ℓh2 . 2/3ℓ = 1/3ℓ2h
и координаты центра тяжести (11.4)
Хc = 1/3ℓ2 h/1/2 ℓh = 2/3ℓ ;
Ус = 1/6ℓ (h12 – h22)/ 1/2ℓh = 1/3(h1 – h2) .
Выразим координаты центра тяжести площади многоугольника (рис. 11. 5, г) с известными координатами вершин относительно координатных осей. Разделим многоугольник на треугольники с общей вершиной в точке А, с координатами А (х1 у1). Составим аналитические выражения площадей этих треугольников в зависимости от координат вершин:
|
х1 |
у1 1 |
= 1/2 [х1 (у2 - у3) + х2 (у3 - у1) + х3 (у1 - у2)] ; |
||
|
F1 = 1/2 |
х2 |
у2 1 |
||
|
F |
х3 |
у3 1 |
||
|
2 = 1/2 [х1 (у3 - у4) + х3 (у4 - у1) + х4 (у1 - у3)] ; |
||||
|
F3 = 1/2 [х1 (у4 - у5) + х4 (у5 - у1) + х5 (у1 - у4)] ; |
||||
|
и координат их центров тяжести |
||||
|
х1 + х2 + х3 |
||||
|
Хc1 =---------------- |
; |
|||
|
3 |
||||
|
х1 + х3 + х4 |
||||
|
Хc2 =---------------- |
; |
|||
|
3 |
||||
|
141 |
|
|
Хc3= |
х1 + х4 + х5 |
|
----------------; |
|
|
3 |
|
|
у1 + у2 + у3 |
|
|
Уc1= |
----------------; |
|
3 |
|
|
Уc2= |
у1 + у3 + у4 |
|
----------------; |
|
|
3 |
|
|
Уc3= |
у1 + у4 + у5 |
|
---------------- . |
|
|
3 |
|
|
Координаты центра тяжести площади многоугольника будут равны: |
|
|
F1Хc1+ F2Хc2+F3Хc3 |
|
| Хc =------------------------------- |
; |
|
F1 + F2 + F3 |
|
|
F1Уc1+ F2Уc2+F3Уc3 |
|
| Уc =------------------------------- |
; |
|
Вычислим координаты центра |
F1 + F2 + F3 |
|
тяжести дуги окружности радиуса R с |
|
центральным углом 2α (рис. 11. 5, д) и осью симметрии Ох. Поэтому Ус = 0 и центр тяжести будет располагаться на оси х с координатой (11. 12)
Хс = 1/L ∫хdℓ .
АВ
Составим аналитические выражения подинтегральных зависимостей: dℓ = R . dφ – бесконечно малый элемент дуги с координатой его центра тяжести
х = R . Соs φ; dφ – бесконечно малый центральный угол, соответствующий элементу дуги dℓ; φ – центральный угол, изменяющийся в пределах от-α до+α.
|
Длина дуги АВ = L = 2αR. Поэтому |
R . Sin φ |
|
|
1 |
+α |
|
|
Хс = ----------∫R Cos φ. R dφ =------------- , |
||
|
2αR |
-α |
α |
где α - угол в радианах.
Выразим координаты центра тяжести кругового сектора ОАВ радиуса R, с центральным углом 2α (рис. 11. 5, е) и осью симметрии Ох. Поэтому Ус = 0 и центр тяжести будет находиться на оси х с координатой (11. 10).
Хс = ∫хdF / F .
F
StudFiles.ru
Определение положения центра тяжести
Статические моменты.
Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями Oz и Oy (рис. 4.1). Выделим элемент площади dF с координатами z, y.
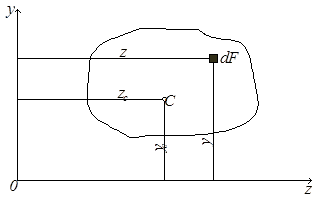
Рис. 4.1
По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражение для момента площади, которое называется статическим моментом. Так dSz = ydF и dSy = zdF – статические моменты элемента площади dF относительно осей Oz и Oy. Просуммировав по всей площади фигуры, получим статические моменты:
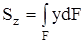 ,
, 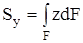 . (4.1)
. (4.1)
Статические моменты имеют размерность единицы длины в кубе (например, см3). Могут быть положительными и отрицательными, знак зависит от положения осей относительно фигуры. Ясно, что относительно каких-то осей статические моменты равны нулю – это оси, проходящие через центр тяжести фигуры.
Рассмотрим задачу о параллельном переносе осей (рис.4.2.).
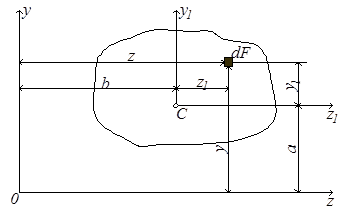 Рис. 4.2 Рис. 4.2 |
Дано: параллельные оси Oz, Oy и Cz1 Cy1, точка C – центр тяжести фигуры, a и b – расстояния между осями, Sz и Sy – известны. Определить: Sz1 и Sy1. Из рис.4.2. следует, что y1 = y – a и z1 = z – b. По определению 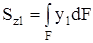 . Подставим у1: . Подставим у1: 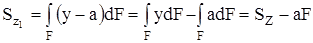 . . |
Получили формулы зависимостей между статическими моментами относительно параллельных осей.
Sz1 = Sz – aF, Sy1 = Sy – bF, (4.2)
где F – площадь фигуры;
a и b – расстояния между осями.
Если оси Cz1 и Cy1 – центральные (проходят через центр тяжести), то Sz1 = Sy1 = 0. Тогда
0 = Sz – ycF, 0 = Sy - zcF.
Статический момент любой фигуры равен произведению площади на расстояние от центра тяжести фигуры до оси:
Sz = Fyc, Sy = Fzc. (4.3)
Отсюда координаты центра тяжести
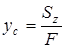 ,
, 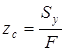 . (4.4)
. (4.4)
По формулам (4.4.) можно найти положение центра тяжести любой плоской фигуры. На рис.4.3. изображена криволинейная лопатка направляющего аппарата гидротурбины. Её необходимо разбить на простые фигуры – прямоугольники, для каждого из которых известна площадь (Fi) и положение центра тяжести (zi, yi) относительно заданных нами осей.
Статический момент площади фигуры относительно данной оси определится как сумма статических моментов каждой части. Координаты центра тяжести
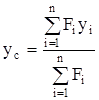 ,
, 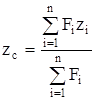 . (4.5)
. (4.5)
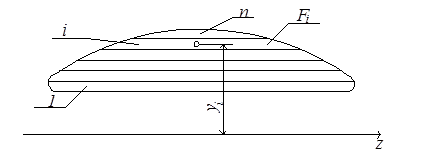
Рис.4.3
studopedia.ru
Центр тяжести это:
Центр тяжести геометрическая точка, неизменно связанная с твёрдым телом, через которую проходит равнодействующая всех сил тяжести, действующих на частицы этого тела при любом положении последнего в пространстве; она может не совпадать ни с одной из точек данного тела (например, у кольца). Если свободное тело подвешивать на нити, прикрепляемые последовательно к разным точкам тела, то направления этих нитей пересекутся в Ц. т. тела. Положение Ц. т. твёрдого тела в однородном поле тяжести совпадает с положением его центра масс (См. Центр масс). Разбивая тело на части с весами pk, для которых координаты xk, yk, zk их Ц. т. известны, можно найти координаты Ц. т. всего тела по формулам: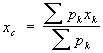
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
dic.academic.ru
Читайте также
![Определение степени тяжести вреда здоровью при дтп Определение степени тяжести вреда здоровью при дтп]() Определение степени тяжести вреда здоровью при дтп
Определение степени тяжести вреда здоровью при дтп![3 Закон ньютона определение 3 Закон ньютона определение]() 3 Закон ньютона определение
3 Закон ньютона определение![Административное право определение Административное право определение]() Административное право определение
Административное право определение![Автомобиль определение Автомобиль определение]() Автомобиль определение
Автомобиль определение![Вес определение Вес определение]() Вес определение
Вес определение![Аренда определение Аренда определение]() Аренда определение
Аренда определение![База данных определение База данных определение]() База данных определение
База данных определение![Бетон определение Бетон определение]() Бетон определение
Бетон определение![Брак это определение в производстве Брак это определение в производстве]() Брак это определение в производстве
Брак это определение в производстве![Власть определение Власть определение]() Власть определение
Власть определение![Восприятие определение Восприятие определение]() Восприятие определение
Восприятие определение- Выберите один из вариантов определения истины это
 Определение степени тяжести вреда здоровью при дтп
Определение степени тяжести вреда здоровью при дтп 3 Закон ньютона определение
3 Закон ньютона определение Административное право определение
Административное право определение Автомобиль определение
Автомобиль определение Вес определение
Вес определение Аренда определение
Аренда определение База данных определение
База данных определение Бетон определение
Бетон определение Брак это определение в производстве
Брак это определение в производстве Власть определение
Власть определение Восприятие определение
Восприятие определение