Понятие окрестности точки
Абсолютная величина (или модуль) действительного числа х - это само число х, если х неотрицательно, и противоположное число -х, если х отрицательно:
![]()
Некоторые свойства абсолютных величин:
-
|х| ≥ 0 (по определению);
-
|х + y| |х| + |y|;
-
|х - y| ≥ |х| - |y|;
-
|хy| = |х||y|;
-
|х/y| = |х|/|y|.
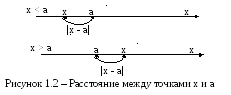 Абсолютная величина разности двух чисел |х - а| означает расстояние между точками х и а числовой прямой как для случая х < а, так и для х > а (см. рис. 1.2). Поэтому, например, решениями неравенства |х - а| < (где > 0) будут точки х интервала ]а - , а + [.
Абсолютная величина разности двух чисел |х - а| означает расстояние между точками х и а числовой прямой как для случая х < а, так и для х > а (см. рис. 1.2). Поэтому, например, решениями неравенства |х - а| < (где > 0) будут точки х интервала ]а - , а + [.
Окрестность точки. Всякий интервал, содержащий точку а, называется окрестностью точки а.
И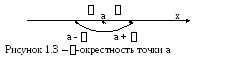 нтервал ]а -, а + [, т.е. множество точек х таких, что |х - а| < (где > 0) называется -окрестностью точки а (см. рис. 1.3).
нтервал ]а -, а + [, т.е. множество точек х таких, что |х - а| < (где > 0) называется -окрестностью точки а (см. рис. 1.3).
Функциональная зависимость
Постоянной величиной (константой) называется величина, сохраняющая одно и то же значение.
Переменной называется величина, которая может принимать различные числовые значения.
Функция – это соответствие (закон), согласно которому каждому элементу х множества X (х X) ставится в соответствие вполне определенный элемент у множества Y (у Y) (этот элемент yобязательно должен быть только один для любого х)..
При этом говорят, что на множестве X задана функция y = f(x).
Переменная х называется независимой переменной (или аргументом), у - зависимой переменной, а буква f обозначает закон соответствия.
Множество X называется областью определения (или существования) функции, а множество Y - областью значений функции.
Если множество X специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной х, т.е. множество таких значений х, при которых функция у = f(х) вообще имеет смысл.
Например, область определения функции ![]() есть промежуток [5; +[, так как под знаком корня должно стоять неотрицательное выражение (х – 5 ≥ 0).
есть промежуток [5; +[, так как под знаком корня должно стоять неотрицательное выражение (х – 5 ≥ 0).
Способы задания функций.Существует несколько способов задания функций:
а) Аналитический способ, если функция задана формулой вида y = f(x). Этот способ наиболее часто встречается на практике. Например, функция ![]() задана аналитически.
задана аналитически.
С помощью формулы функция может быть задана явно или неявно. Задание будет явным, если правая часть формулы не содержит зависимую переменную. Например, в формуле ![]() правая часть не содержит y, поэтому функция задана явно. Пример неявного задания функции – выражение x3 + y2 = 2. С помощью этого выражения неявно заданы две функции –
правая часть не содержит y, поэтому функция задана явно. Пример неявного задания функции – выражение x3 + y2 = 2. С помощью этого выражения неявно заданы две функции – ![]() для y > 0 и
для y > 0 и ![]() для y < 0.
для y < 0.
б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции f(x). Например, прайс-лист, в котором каждому номеру товара соответствует его цена.
в) Графический способ состоит в изображении графика функции - множества точек (х, y), абсциссы которых есть значения аргумента х, а ординаты - соответствующие им значения y (см. рисунок 1.3).
Основные свойства функций
1. Четность и нечетность. Функция y = f(x) называется четной для любых значений х из области определения, если f(-x) = f(x), и нечетной, если f(-x) = -f(x). В противном случае функция называется функцией общего вида.
Например, функция у = х2 является четной, так как (-х)2 = х2; а функция у = х3 – нечетной, так как (-х)3 = -х3. Функция у = f(x) = х2 +х3 является функцией общего вида, так как f(-x) = (-х)2 +(-х)3 = х2 - х3. При этом f(-x) f(x) и f(-x) - f(x).
График четной функции симметричен относительно оси ординат (например, функции у = х2), а график нечетной функции симметричен относительно начала координат (например, график функции у = х3).
2. Монотонность. Функция y = f(x) называется возрастающей (убывающей) на некотором промежутке, еcли большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть х1, х2 X и х2 > х1. Тогда функция возрастает на промежутке X, если f(x2) > f (х1) и убывает, если f(x2) < f (х1).
В обоих случаях функции называются строго монотонными. Если два последних неравенства – нестрогие (т.е. f(x2) ≥ f (х1) и f(x2) f (х1)), то функции называют соответственно неубывающими и невозрастающими.
Например, функция у = х2 убывает для неположительных значений аргумента (т.е. на промежутке ]-; 0]) и возрастает для неотрицательных.
3. Ограниченность. Функцияy= f(x) называетсяограниченнойна некотором промежуткеX, если существует такое положительное число М, что модуль значения функции не превышает этого числа для любого аргумента из этого промежутка. (М > 0: |f(x)|Mдля любого хX)
В противном случае функция называется неограниченной.
Например, функция у = cosх ограничена на всей числовой оси, так как |cosх|1. Функция у = х не ограничена на ]-; +[.
Если в определении рассматривать не модуль значения функции, а само значение, которое должно быть не меньше или не больше числа М, то можно говорить об ограниченности снизу или сверху.
4. Периодичность. Функция y = f(x) называется периодической с периодом Т 0, если для любых х из области определения f(х + Т) = f(x).
Например3, функция у = sin х имеет период Т = 2, так как sin (х +2) = sin х.
Обратная функция. Если для функции y = f(x) различным аргументам х1 х2 соответствуют различные значения функции y1 y2, то можно определить функцию x = (y), которая каждому число y = f(x) ставит в соответствие число х. Такую функцию называют обратной для f и обозначают f-1.(не следует путать это обозначение с возведением в степень (-1)).
Из этого определения следует, что для любой строго монотонной функции существует обратная функция.
Например, для функции у=ах обратной будет функция x=lоgaу (или в обычных обозначениях зависимой и независимой переменных у= lоgах).
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (относительно прямой y = x) (см. рис. 1.3).

Сложная функция. Пусть функция y = f (u) есть функция от переменной u, определенной на множестве U c областью значений Y, а переменная u, в свою очередь, является функцией u = (х) от переменной х, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y = f [ (х)] называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции).
Например, у = lg sin х — сложная функция, так как ее можно представить в виде у= lg u, где u = sin х.
StudFiles.ru
Определение 4. Определение предела последовательности
Предел последовательности
Примеры.
Предельная точка.
Окрестность точки.
Определение 2. Окрестностью точки A на числовой прямой называется любой интервал CD, содержащий эту точку. ε - окрестностью точки A называется интервал (A - ε, A + ε), или, в виде неравенства, .(см. Рис. 3. а)).
ε - окрестность точки A обозначается: Uε (A) или ε(A) и записывается с помощью неравенства: Uε (A) : .
Определение 2'. Проколотой окрестностью точки A на числовой прямой называется совокупность интервалов CA ∪ AD, то есть интервал CD не содержащий точку A. Проколотой ε - окрестностью точкиA называется интервал совокупность интервалов (A - ε, A) ∪ (A, A + ε),
или, в виде двойного неравенства, .( см. Рис. 3. б)).
Проколотая ε - окрестность точки A обозначается или и записывается с помощью двойного неравенства неравенства:
: .
Рис. 3. а) Рис. 3. б)
Определение 3. (геометрическое) Точка a называетсяпредельной точкойпоследовательности, если в любой ее окрестности содержится бесконечное множество точек (элементов) последовательности.
Определение 3'. (формализованное)
a - предельная точка .
a - предельная точка, если для любого положительного ε и для любого номера последовательности N всегда найдется элемент последовательности с номером n> N, лежащий в ε - окрестности точки a.
Пояснение (к определению 3' ).Если для любого номера последовательности N всякий раз найдется n-ый элемент (n > N) такой, что он будет отличаться от a меньше, чем на ε ( ), в ε - окрестности точки a наберется бесконечное число элементов последовательности.
Формализованные определения позволяют проводить строгие математические доказательства, геометрические - позволяют понять формализованное определение. Геометрические доказательства без наличия строго формализованного доказательства чаще всего доказательством не считают.
o Последовательность{xn}, где xn = - (1)n имеет две предельные точки a1 = 1 и a2 = - 1 (Рис. 4. а)).
o Последовательность{xn}, где xn = 1/n имеет одну предельную точку a = 0 (Рис. 4. б)).
o Последовательность{xn}, где имеет три предельные точки . (Докажите самостоятельно)
o Последовательность{xn}, где имеет n предельных точек.
o Последовательность{xn}, где не имеет предельных точек (у нас пока не введено понятия окрестности для бесконечности ∞, поэтому пока мы не можем сказать, что у данной последовательности есть предельная точка, равная ∞).
Рис. 4. а). Рис. 4. б).
(формализованное) Число A называется пределом последовательности {xn}, если для любого положительного ε найдется номер последовательности N(ε), вообще говоря, зависящий от ε такой, что для любого n > N, все элементы последовательности с номером n >N попадут в ε - окрестность точки A: .
Пояснение.Для любого сколь угодно малого ε всякий раз найдется такой номер N последовательности, что с ростом n (n > N) значения элементов последовательности становятся сколь угодно близкими к A, то есть отличаются от A меньше, чем на ε (Рис. 4. б)), это и означает, что A - предел.
Геометрически: если A предел последовательности {xn}, то за пределами ε - окрестности точки A окажется лишь конечное число точек (элементов) последовательности.
o На рисунке 4.а) последовательность { ( - 1)n } имеет две предельные точки, и, за пределами ε - окрестности одной точки лежит бесконечное число точек той же последовательности, значит данная последовательность не имеет предела.
o На рисунке 4.б) последовательность {1/n}имеет одну предельную точку, и она является пределом последовательности.
ü Но не следует думать, что наличие единственной предельной точки гарантирует существования предела. Приведем контрпример:
Контрпример.Рассмотрим последовательность, состоящую из смешанного набора точек двух последовательностей {n} и {1/n}. Ее элементы:
1, 1, 1/2,1/3, 3, 1/4, 4, …1/n, n, ….
Условно обозначим эту последовательность {1/n, n}. У нее имеется единственная предельная точка 0, но предела у последовательности нет. Так как за пределами окрестности точки 0 имеется бесконечное число элементов последовательности. (Рис. 5)
Рис. 5
Контрпример позволяет опровергнуть утверждение и не проводить длинное, сложное доказательство. Мы предположили, что у всех числовых последовательностей с единственной предельной точкой существует предел. Мы привели контрпример и показали, что это не так.
Задачи. С помощью определения предела (формализованного) доказать
| a) , c) , e) ∄ , | b) , d) , f) ∄ . |
a)
Докажем , исходя из определения предела.
По сути, нам надо определить при каких n будет верно неравенство .
(n - натуральное число, всегда положительное).
Положим , где функция - выражает собой целую часть числа x.
Например, целая часть числа 2,89 есть число 2: [2,89] = 2.
Имеем,
.
Это и означает, что .
b) ,
Исходя из определения предела, определим при каких n будет верно неравенство .
.
Положим ,
тогда,
. .
Это и означает, что .
c) ,
Исходя из определения предела, определим, при каких n будет верно неравенство .
.
Для того чтобы увеличить дробь нужно увеличить числитель и уменьшить знаменатель. Проведем оценки:
| Увеличиваем слагаемые числителя | Уменьшаем слагаемые знаменателя |
Положим ,
тогда, . .
Это и означает, что .
d) ,
Исходя из определения предела, определим, при каких n будет верно неравенство .
Здесь мы домножили числитель и знаменатель на выражение, дающее в числителе формулу квадрата разности .
Для того чтобы увеличить дробь нужно уменьшить знаменатель:
| Уменьшаем слагаемые знаменателя |
.
Положим ,
тогда, .
Мы доказали, что .
e) ∄
, так как с ростом n значения {(-1)n} не становятся сколь угодно
близкими к 1. Например, при ε = 1 условие близости
не выполняется при всех нечетных n и, следовательно,
не существует такое число N, чтобы для всех n>N было .
, так как с ростом n условие близости
не выполняется при всех четных n.
, так как для ε = ½ с ростом условие близости
не выполняется при всех n.
f) ∄ не существует. Докажите самостоятельно.
Указание: последовательность{ } имеет три предельные точки
.
| Для n = 3k+1, где k - любое натуральное число. | |
| Для n = 3k+2, где k - любое натуральное число. | |
| Для n = 3k, где k - любое натуральное число. |
Теорема. 1. (о единственности предела). Если предел последовательности существует, то он единственный.
Доказательство. Позже.
Определение 5. Определение ограниченной последовательности.
Последовательности {xn}, называется ограниченной, если
∃ M, что .
Теорема. 2. (об ограниченности последовательности, имеющей предел). Если предел последовательности имеет предел, то она ограничена.
Доказательство. Позже.
Замечание. Обратное: если последовательность ограничена, она имеет предел, - неверно.
Контрпримеры. {(-1)n}, { }, {n}… Придумайте еще примеры.
Следствие. Если последовательность не ограничена, то она не имеет предела.
Доказательство. Если последовательность не ограничена и имеет предел, то по Теореме 2 она ограничена.
studopedia.ru
2Определения
Здесь > 0, поэтому последнее неравенство выполняется для всех только при неположительном дискриминанте, т.е.
= 4 2 − 4 6 0,
, 2 6 ‖ ‖2 · ‖ ‖2,
, 6 ‖ ‖ · ‖ ‖.
Равенство , = ‖ ‖ · ‖ ‖ выполняется только в случае + , + = 0, т.е. + = 0, а это и означает, что и линейно зависимы. [:|||||:]
Теорема 25.2 (Неравенство Минковского). Для любых двух векторов= ( 1, . . . , ) и
= ( 1, . . . , ) имеет место неравенство
|
+ |
||||||||
|
( + )2 6 |
2 |
2. |
||||||
|
=1 |
=1 |
=1 |
||||||
|
∑ |
∑ |
∑ |
||||||
Доказательство. По формуле квадрата суммы и в силу неравенстваКоши-Буняковского:
|
( + ) = |
+ |
2 + |
6 |
+ 2 |
. |
||||||||||||||||||||||||||||
|
+ |
|||||||||||||||||||||||||||||||||
|
· |
|||||||||||||||||||||||||||||||||
|
=1 |
=1 |
=1 |
=1 |
=1 |
=1 |
=1 |
=1 |
||||||||||||||||||||||||||
|
∑ |
∑ |
∑ |
∑ |
∑ |
∑ |
∑ |
∑ |
||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||
|
Правая часть этого неравенства может быть записана в виде квадрата суммы: |
|||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||
|
2 |
+ 2 |
2 |
· |
2 |
2 |
= |
2 |
2 |
. |
||||||||||||||||||||||||
|
+ |
+ |
=1 |
|||||||||||||||||||||||||||||||
|
=1 |
=1 |
=1 |
=1 |
=1 |
|||||||||||||||||||||||||||||
|
∑ |
∑ |
∑ |
∑ |
∑ |
∑ |
||||||||||||||||||||||||||||
|
Таким образом |
|||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||
|
∑ |
∑ |
∑ |
|||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||||||||||||
|
=1 ( + ) |
6 =1 |
+ =1 |
, |
||||||||||||||||||||||||||||||
|
6 |
+ |
||||||||||||||||||||||||||||||||
|
( |
+ )2 |
2 |
2. |
||||||||||||||||||||||||||||||
|
=1 |
=1 |
=1 |
|||||||||||||||||||||||||||||||
|
∑ |
∑ |
∑ |
|||||||||||||||||||||||||||||||
[:|||||:]
2.1 Классификация точек
Будем называть открытым шаром радиуса с центром в точке множество R , азакрытым шаром радиуса с центром в точке множество R .Сферой же радиуса с центром в будем называть множество ( , ) = . Принято обозначать открытый шар радиуса с центром в как U ( ). Подробнее о связи с окрестностью точки будет сказано ниже.
Например, в двумерном случае открытый шар — это множество всех точек круга радиуса (не считая границу), закрытый — сам круг радиуса , а сфера — это окружность радиуса .
Пусть имеется множество R . Тогда все точки пространства можно разделить на 3 непересекающихся множества:
70
внутренняя для , если > 0 : U ( ) . Фактически это означает, что существует такой открытый шар вокруг , который целиком содержится в .
внешняя для , если > 0 : U ( ) ∩ = ?. Это означает, что существует такой открытый шар вокруг , который не содержится в .
граничная, если > 0′,′′ U ( ) :′ ,′′ / . Заметим, что граничная точка не является ни внутренней, ни внешней. Иначе говоря, часть точек из открытого шара вокруг принадлежит , а часть — нет.
2.2Открытые и замкнутые множества
Будем называть множество открытым, если оно состоит только из внутренних точек. Множество называетсязамкнутым, если оно содержит также все свои граничные точки.Границей множества ∂ будем называть множество всех граничных точек .
Из определений ясно, что если — открытый шар, то ∂ ̸ , а если замкнутый, то ∂ . Однако стоит понимать, что множество может быть не открытым и не замкнутым, например:
|
= |
{ R | |
{ ( , ) 6 |
, |
если 1 |
— иррационально}. |
|
( , ) |
, |
если 1 |
— рационально |
Очевидно, что в этом множестве есть граничные точки, но не все.
Важно также понимать, что граница множества — необязательно подмножество самого множества. Рассмотрим следующий пример:
= ( , ) .
Нетрудно понять, что ∂ = 0 6 , 6 1, т.е. ∂ . Более того, из определений этих множеств следует, что | | = 0, в то время как |∂ | = |R|, т.е. | | < |∂ |.
Будем называть точку предельной для , если > 0 в U ( ) есть точки из , отличные от . Из этого определения следует, что — предельная точка т.и.т.т., когда > 0 в U ( ) содержится бесконечно много точек из (тут все аналогично одномерному случаю).
Теорема 25.3. Множество замкнуто т.и.т.т., когда содержит все свои предельные точки.
Доказательство.
Необходимость.
, будучи замкнутым, не содержит в себе только внешние точки. Но предельные точки по определению не являются внешними, значит они заведомо входят в .
Достаточность.
Предположим, что не замкнуто и * — граничная точка, такая что* / , т.е. > 0
в U ( *) есть точки из , отличные от* (т.к.* / по предположению). Но это не что иное, как определение предельной точки, т.е.* — предельная точка. Но тогда по 1 части теоремы* , т.е. получили противоречие.
[:|||||:]
Предельная и граничная точка — разные понятия! Например, рассмотрим множество
= ( , ) {(2, 2)}. Тогда:
71
Точка (0, 0) является предельной, но не граничной.
Точка (1, 0) и граничная, и предельная.
Точка (2, 2) граничная (т.к. в любом открытом шаре вокруг нее есть она сама и точки не из ), но не предельная.
2.3Окрестность точки
Теперь поговорим об окрестностях. В многомерном пространстве можно определить 2 вида взаимозаменяемых (как будет показано позже) окрестностей. Обычно в доказательствах принято использовать шаровую окрестность U ( ) (т.е. открытый шар), но возможен и другой вариант.
Назовем прямоугольной окрестностью точки окрестность (1,2, . . . , ), состоящую из всех точек R , таких что |1 −1| -мерномпространстве со сторонами (21, 22, . . . , 2 ). Однако вид окрестности не имеет значения (в одномерном случае они вообще одинаковы):
Теорема 25.4. Любая шаровая-окрестностьточки содержит в себе некоторую прямоугольную окрестность, и наоборот, любая прямоугольная окрестность точки содержит в себе некоторую шаровую-окрестность.
Доказательство.
|
Пусть имеется -окрестностьточки . Тогда по определению√ =1( − )2 < , из чего |
|||||||||||||||||||||||||
|
| |
− |
| |
принадлежит прямоугольной |
||||||||||||||||||||||
|
следует, что |
1, |
< , а это значит, что |
∑ |
||||||||||||||||||||||
|
-окрестности. |
|||||||||||||||||||||||||
|
Пусть теперь ( 1,2, . . . , ). Тогда |
√ |
< | 1 −1|+|2 −2|+· · ·+| − | |
|||||||||||||||||||||||
|
=1(− )2 |
|||||||||||||||||||||||||
|
1 + 2+ |
· · · |
+ |
6 |
· |
max |
1 |
2 |
} |
∑ |
||||||||||||||||
|
{ |
, , . . . , |
= , т.е. |
U ( ). |
||||||||||||||||||||||
[:|||||:]
Будем называть множество ограниченным, если > 0 : | | 6 . Здесь запись | | фактически означает ‖ ‖. Далее мы везде будем использовать | |, если из контекста понятно, что имеется в виду. Это удобно, поскольку многие определения и теоремы в многомерном случае формулируются точно так же, как и в одномерном, если не учитывать смысл, который вкладывается в запись | |.
Будем говорить, что точки и связаны непрерывной кривой ( ), если ( ) C[ , ] :( ) = , ( ) = . Иными словами, есть некоторая непрерывная кривая, каждая точка ( ) которой задается как ( ) = (1(1),2(2), . . . , ( )), причем первая точка кривой совпадает с , а последняя — с , т.е. она соединяет точки и , причем ее траектория может быть абсолютно любой.
Соответственно, множество называется связным, если′,′′ ( ), соединяющая′ и′′, причем ( ) . Например, множество = 2 +2 6 1 связно, а′ =( , ) — нет, т.к. не существует кривой, целиком содержащейся в′, которая бы соединяла, например,′ = (0, 0) и′′ = (3, 3).
72

3Числовые последовательности в R
Как и в одномерном случае, у нас есть некоторое отображение из N в R , т.е. каждомуN ставится в соответствие = ( 1 ,2 , . . . , ) R . Обратите внимание, что означает не возведение в степень, а-ыйчлен последовательности.
Теперь введем понятие сходимости в многомерном пространстве:
lim = > 0 ( ) > 0 : > | − | < .
→∞
Заметим, что это определение абсолютно аналогично таковому в одномерном случае за исключением смысла | − | (теперь это ( , )).
Теорема 25.5. Для любогоконечномерного пространстваR выполняется:{ } −−−→
→∞
{ } −−−→ .
→∞
Доказательство.
Необходимость.
По определению > 0 ( ) > 0 : > ∑( − )2
|
означает, что |
. |
=1 |
|||||||||||
|
{ |
} −−−→ |
||||||||||||
|
→∞ |
|||||||||||||
|
Достаточность. |
|||||||||||||
|
По определению |
и > 0 |
( ) : > | − | 6 |
√ |
. Но если выбрать |
|||||||||
|
< · 2 |
= 2 ( , ) < . |
||||||||||||
|
= max , то > =1( − )2 |
|||||||||||||
|
∑ |
|||||||||||||
[:|||||:]
Таким образом, все теоремы доказываются, опираясь на уже доказанное для одномерного случая. Например:
Теорема 25.6 (Критерий Коши). Последовательность{ } сходится т.и.т.т., когда она является фундаментальной, т.е.> 0 ( ) : > , N | + − | < .
Доказательство.
Необходимость.
Полностью аналогично одномерному случаю.
Достаточность.
 — фундаментальная. Тогда > 0 ( ) : > , N∑(+ − )2
— фундаментальная. Тогда > 0 ( ) : > , N∑(+ − )2
=1
| + − | < , а это определение фундаментальной последовательности для одномерного случая. Каждая координатная последовательность сходится, значит из предыдущей теоремы следует, что и { } сходится.
[:|||||:]
Теорема 25.7 (Теорема Больцано-Вейерштрасса). Если{ } ограничена, то существует
ее сходящаяся подпоследовательность, т.е. { } −−−→ .
→∞
73
StudFiles.ru
Проколотая окрестность это:
Проколотая окрестностьОкре́стность точки — множество, содержащее данную точку, и близкие к ней.
Содержание
|
Определения
- Пусть задано топологическое пространство
 , где X — произвольное множество, а
, где X — произвольное множество, а  — определённая на X топология. Множество
— определённая на X топология. Множество  называется окрестностью точки
называется окрестностью точки  , если существует открытое множество
, если существует открытое множество  такое, что
такое, что  .
.
- Аналогично окрестностью множества
 называется такое множество
называется такое множество  , что существует открытое множество
, что существует открытое множество  , для которого выполнено
, для которого выполнено  .
.
Замечания
- Приведённые выше определения не требуют, чтобы окрестность V была открытым множеством, но лишь чтобы она содержала открытое множество U. Некоторые авторы настаивают на том, что любая окрестность открыта. Тогда окрестностью множества называется любое содержащее его открытое множество. Это не принципиальное для развития дальнейшей топологической теории различие. Однако, в каждом случае важно фиксировать терминологию.
- Прямо из определения следует, что V является окрестностью множества M тогда и только тогда, когда V есть окрестность любой точки
 .
.
Проколотая окрестность
Множество 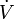 называется проко́лотой окре́стностью (вы́колотой окрестностью) точки
называется проко́лотой окре́стностью (вы́колотой окрестностью) точки 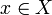 , если
, если
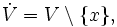
где V — окрестность x.
Строго говоря, проколотая окрестность не является окрестностью в смысле данного выше определения.
Пример
Пусть дана вещественная прямая со стандартной топологией. Тогда [ − 1,2] является окрестностью, а ( − 1,2) — открытой окрестностью точки 0. Множество  является проколотой окрестностью 0.
является проколотой окрестностью 0.
См. также
- ε-окрестность.
Wikimedia Foundation. 2010.
dic.academic.ru
Глава 2. Предел числовой последовательности
2.1. Определение окрестности точки, числовой
последовательности и ее предела
2.1.1. Числовая последовательность
-
Что называется числовой последовательностью? Как обозначается и каким образом задается числовая последовательность. Приведите примеры числовых последовательностей.
-
Какая последовательность называется постоянной последовательностью, конечной последовательностью? Приведите примеры таких последовательностей.
-
Приведите примеры геометрической и арифметической прогрессий.
-
Найдите пятый член последовательностей:
а) ![]() , если
, если![]() ,
,
б) ![]() , если
, если![]() ,
,
в) ![]() , если
, если![]() ,
,![]() ,
,
г) ![]() ,
,
д) ![]() − последовательность всех делителей числа 20, расположенных в порядке возрастания,
− последовательность всех делителей числа 20, расположенных в порядке возрастания,
е) 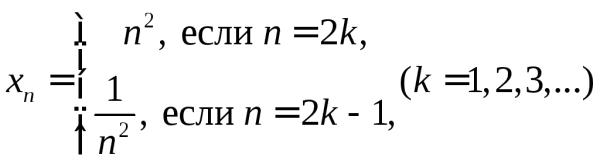 ,
,
ж) ![]() − последовательность,n член которой − n цифра числа
− последовательность,n член которой − n цифра числа ![]() ,
,
з) ![]() ,
,
и) ![]() − геометрическая прогрессия, у которой первый член
− геометрическая прогрессия, у которой первый член![]() , а знаменатель прогрессии
, а знаменатель прогрессии![]() ,
,
к) ![]() − арифметическая прогрессия, у которой первый член
− арифметическая прогрессия, у которой первый член![]() , а разность прогрессии
, а разность прогрессии![]() .
.
-
Дайте определения ограниченной сверху (снизу), ограниченной, неограниченной последовательности. Каков геометрический смысл понятия “ограниченная последовательность”? Приведите соответствующие примеры.
-
Являются ли последовательности ограниченными сверху (снизу), ограниченными, неограниченными:
а) ![]() ,
,
б) ![]() ,
,
в) ![]() ,
,
г) ![]() ,
,
д) ![]() .
.
2.1.2. Предел числовой последовательности
-
Запишите определение предела последовательности с помощью логических знаков.
-
Дайте определения сходящейся и расходящейся последовательности. Приведите примеры таких последовательностей.
-
Пусть последовательность
 и число
и число удовлетворяют условию:
удовлетворяют условию:
![]() такое, что
такое, что ![]() . Всякая ли сходящаяся к
. Всякая ли сходящаяся к![]() последовательность удовлетворяет этому условию?
последовательность удовлетворяет этому условию?
-
Пусть
 .
.
а) Могут ли все члены последовательности быть положительными (отрицательными), если ![]() ?
?
б) Может ли последовательность иметь бесконечно много отрицательных (равных нулю) членов, если ![]() ?
?
в) Докажите, что ![]() ,
,![]() .
.
-
Пусть последовательность сходится. Является ли сходящейся последовательность, которая получается из исходной, если:
а) из нее удалить конечное число членов, а оставшиеся заново перенумеровать в порядке их следования,
б) к ней добавить конечное число членов, перенумеровав члены последовательности в порядке их следования,
в) в ней изменить произвольным образом конечное число членов?
-
Сформулировать на языке “
 ”определение того, что
”определение того, что
а) ![]() ,
,
б) не существует ![]() .
.
-
Докажите по определению, что предел
 равен
равен .
. -
Докажите, что если
 , то
, то .
. -
Привести пример последовательности
 , удовлетворяющей условию
, удовлетворяющей условию и такой, что
и такой, что
а) она не имеет предел,
б) она имеет предел. Может ли этот предел быть положительным?
2.1.3 Окрестность точки, геометрический смысл предела последовательности
-
Дайте определение окрестности точки
 .
. -
Приведите геометрическую иллюстрацию предела последовательности.
-
Пусть в некоторой окрестности точки
 лежит бесконечно много членов последовательности
лежит бесконечно много членов последовательности . Следует ли из этого условия, что:
. Следует ли из этого условия, что:
а) ![]() ,
,
б) никакая точка вне этой окрестности не является пределом последовательности ![]() ,
,
в) ![]() ограничена?
ограничена?
-
Пусть в любой окрестности точки
 лежит бесконечно много членов последовательности
лежит бесконечно много членов последовательности . Следует ли отсюда, что
. Следует ли отсюда, что ?
?
StudFiles.ru
Читайте также
![Определение документооборота с точки зрения информации Определение документооборота с точки зрения информации]() Определение документооборота с точки зрения информации
Определение документооборота с точки зрения информации![Точка определение Точка определение]() Точка определение
Точка определение![Определение пикетажного положения нулевых точек Определение пикетажного положения нулевых точек]() Определение пикетажного положения нулевых точек
Определение пикетажного положения нулевых точек![Определение момента силы относительно точки Определение момента силы относительно точки]() Определение момента силы относительно точки
Определение момента силы относительно точки![Акт определение Акт определение]() Акт определение
Акт определение- Актив определение
![Административное право определение Административное право определение]() Административное право определение
Административное право определение![Аренда определение Аренда определение]() Аренда определение
Аренда определение![База данных определение База данных определение]() База данных определение
База данных определение![Бетон определение Бетон определение]() Бетон определение
Бетон определение![Брак это определение в производстве Брак это определение в производстве]() Брак это определение в производстве
Брак это определение в производстве![Власть определение Власть определение]() Власть определение
Власть определение
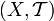 , где X — произвольное множество, а
, где X — произвольное множество, а 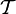 — определённая на X топология. Множество
— определённая на X топология. Множество 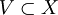 называется окрестностью точки
называется окрестностью точки 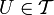 такое, что
такое, что 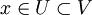 .
.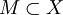 называется такое множество
называется такое множество 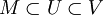 .
.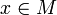 .
. Определение документооборота с точки зрения информации
Определение документооборота с точки зрения информации Точка определение
Точка определение Определение пикетажного положения нулевых точек
Определение пикетажного положения нулевых точек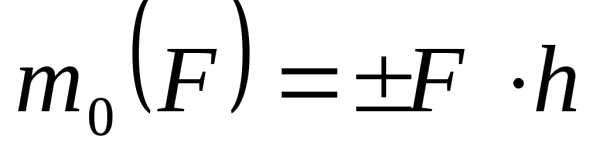 Определение момента силы относительно точки
Определение момента силы относительно точки Акт определение
Акт определение Административное право определение
Административное право определение Аренда определение
Аренда определение База данных определение
База данных определение Бетон определение
Бетон определение Брак это определение в производстве
Брак это определение в производстве Власть определение
Власть определение