ПРОСТОЕ ЧИСЛО это:
ПРОСТОЕ ЧИСЛО- натуральное (целое положительное) число р>1, имеющее только два делителя 1 и p: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ... Числа, имеющие не менее трех различных делителей, наз. составными. Понятие П. ч. является основным ири изучении делимости натуральных чисел. Так, основная теорема элементарной теории чисел утверждает, что всякое натуральное число, отличное от единицы, либо простое, либо, если оно составное, может быть представлено в виде произведения простых чисел. При этом такое представление единственно (с точностью до расположения сомножителей). Запись этого произведения в виде степеней одинаковых П. ч., а самих П. ч. в порядке возрастания, дает канонич. разложение натурального числа:

С помощью канонич. разложений натуральных чисел al, а 2, . . ., а k находят наибольший общий делитель d=(a1, а 2, . . ., ak).и наименьшее общее кратное m=[a1, а 2, . . ., ak] этих чисел. С помощью канонич. разложения натурального числа пвычисляются значения теоретико-числовых функций t(n), S(п).и j(n), к-рые обозначают соответственно число делителей, сумму делителей числа пи количество натуральных чисел  , взаимно простых с п(т. е. таких, что ( т, n)=1):
, взаимно простых с п(т. е. таких, что ( т, n)=1):

Существенной особенностью этих формул является их зависимость от арифметич. структуры натурального аргумента п.
П. ч. играют роль своеобразных "кирпичиков", из к-рых строятся вес остальные натуральные числа. Еще в 3 в. до н. э. Евклид доказал бесконечность множества П. ч., а Эратосфен нашел способ отсеивания П. ч. из множества натуральных чисел (см. Эратосфена решето). Л. Эйлер (L. Euler) нашел доказательство бесконечности множества П. ч., основанное на использовании средств математич. анализа. Дальнейшее развитие аналитич. метода Эйлера оказалось очень плодотворным (см. Аналитическая теория чисел). П. Л. Чебышев открыл ряд новых законов, к-рым подчиняются П. ч. В частности, с помощью элементарных рассуждений, использующих канонич. разложение для числа n!, П. Л. Чебышев нашел неравенства, к-рым должно удовлетворять количество p(х). простых чисел  :
:

где a1 - нек-рые положительные константы. Наиболее глубокие закономерности, к-рым подчиняется поведение последовательности П. ч., были получены путем углубления исходных идей П. Л. Чебышева с помощью аналитических и, в ряде случаев, элементарных методов (см. Распределение простых чисел).
П. ч. связаны не только с мультипликативной, но и с аддитивной структурой натуральных чисел. Достаточно характерной в этом отношении является Гольдбаха проблема о разбиении натуральных чисел на сумму трех П. ч., решенная в 1937 И. М. Виноградовым (см. Аддитивная теория чисел). Изучение законов разложения П. ч. в алгебраич. полях проливает свет на свойства обычных П. ч. Напр,, рассматривая закон разложения П. ч.  в поле гауссовых чисел, получают теорему Гаусса: р=а 2+b2 тогда и только тогда, когда
в поле гауссовых чисел, получают теорему Гаусса: р=а 2+b2 тогда и только тогда, когда  (mod 4).
(mod 4).
Существует много пока (1983) еще не решенных проблем, относящихся к П. ч. Напр.:
будет ли бесконечным множество П. ч. Мерсенна:
р=2q-1, где q- простое; будет ли бесконечным множество П. ч. Ферма:
 , где
, где  - целое;
- целое;
существует Ли бесконечное множество П. ч. р 1 и р 2 "близнецов", т. е. таких, что р 1- р 2=2.
Экспериментальные и эвристич. соображения свидетельствуют в пользу положительного решения сформулированных выше проблем и др. аналогичных задач.
Лит.:[1] Xассе Г., Лекции по теории чисел, пер. с нем., М., 1953 Б. М. Бредихин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Как найти простые числа?
Числа бывают разными: натуральными, естественными, рациональными, целыми и дробными, положительными и отрицательными, комплексными и простыми, нечетными и четными, действительными и др. Из данной статьи можно узнать, что такое простые числа.

Какие числа называют английским словом “симпл”?
Очень часто школьники на один из самых несложных на первый взгляд вопросов математики, о том что такое простое число, не знают, как ответить. Они часто путают простые числа с натуральными (то есть числа, которые используются людьми при счете предметов, при этом в некоторых источниках они начинаются с нуля, а в других - с единицы). Но это совершенно два разных понятия. Простые числа - это, натуральные, то есть целые и положительные числа, которые большее единицы и которые имеют всего лишь 2 натуральных делителя. При этом один из этих делителей - это данное число, а второй – единица. Например, три - это простое число, поскольку он не делится без остатка ни на какое другое число, кроме себя самого и единицы.
Составные числа
Противоположностью простых чисел являются составные. Они также являются натуральным, также больше единицы, но имеют не два, а большее количество делителей. Так, например, числа 4, 6, 8, 9 и т. д. являются натуральными, составными, но не простыми числами. Как видите – это в основном четные числа, но не все. А вот “двойка” – четное число и “первый номер” в ряду простых чисел.
Последовательность
Чтобы построить ряд простых чисел, необходимо совершить отбор из всех натуральных чисел с учетом их определения, то есть нужно действовать методом от противного. Необходимо рассмотреть каждое из натуральных положительных чисел на предмет того, имеет ли оно более двух делителей. Давайте постараемся построить ряд (последовательность), который составляют простые числа. Список начинается с двух, следующим идет три, поскольку оно делится только на себя и на единицу. Рассмотрим число четыре. Имеет ли оно делители, кроме четырех и единицы? Да, это число 2. Значит, четыре не является простым числом. Пять также является простым (оно, кроме 1 и 5, ни на какое другое число не делится), а вот шесть – делится. И вообще, если проследить за всеми четными числами, то можно заметить, что кроме “двух”, ни одно из них не является простым. Отсюда сделаем вывод, что четные числа, кроме двух, не являются простыми. Еще одно открытие: все числа, делящиеся на три, кроме самой тройки, будь то четные или нечетные, также не являются простыми (6, 9, 12, 15, 18, 21, 24, 27 и т.д.). То же самое касается и чисел, которые делятся на пять и на семь. Все их множество также не является простым. Давайте подведем итоги. Итак, к простым однозначным числам относятся все нечетные числа, кроме единицы и девятки, а из четных – только “два”. Сами десятки (10, 20,... 40 и др.) не являются простыми. Двузначные, трехзначные и т. д. простые числа можно определить, исходя из вышеизложенных принципов: если они не имеют других делителей, кроме их самих и единицы.

Теории о свойствах простых чисел
Существует наука, которая изучает свойства целых чисел, в том числе и простых. Это раздел математики, которая называется высшей. Помимо свойств целых чисел, она также занимается алгебраическими, трансцендентными числами, а также функциями различного происхождения, связанными с арифметикой этих чисел. В этих исследованиях, помимо элементарных и алгебраических методов, также используются аналитические и геометрические. Конкретно изучением простых чисел занимается “Теория чисел”.
Простые числа — “строительные блоки” натуральных чисел
В арифметике есть теорема, которая называется основной. Согласно ей, любое натуральное число, кроме единицы, можно представить в виде произведения, множителями которого являются простые числа, причем порядок следования множителей единственен, этот означает, что и способ представления единственен. Он называется разложением натурального числа на простые множители. Есть и другое название этого процесса – факторизация чисел. Исходя из этого, простые числа можно назвать “строительным материалом”, "блоками" для построения натуральных чисел.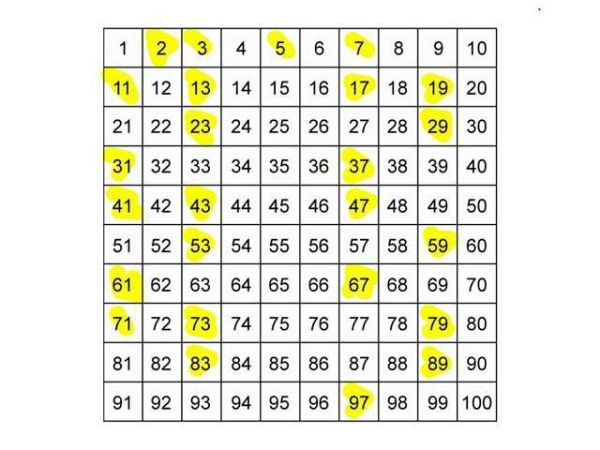
Поиск простых чисел. Тесты простоты
Множество ученых разных времен пытались найти какие-то принципы (системы) для нахождения списка простых чисел. Науке известны системы, которые называются решето Аткина, решето Сундартама, решето Эратосфена. Однако они не дают каких-то существенных результатов, и для нахождения простых чисел используется простая проверка. Также математиками были созданы алгоритмы. Их принято называть тестами простоты. Например, существует тест, разработанный Рабином и Миллером. Его используют криптографы. Также существует тест Каяла-Агравала- Саскены. Однако он, несмотря на достаточную точность, очень сложен в вычислении, что принижает его прикладное значение.
Имеет ли множество простых чисел предел?
О том, что множество простых является бесконечностью, писал в книге “Начала” древнегреческий ученый Евклид. Он говорил так: “Давайте на минуту представим, что простые числа имеют предел. Тогда давайте перемножим их друг с другом, а к произведению прибавим единицу. Число, полученное в результате этих простых действий, не может делиться ни на одно из ряда простых чисел, потому что в остатке всегда будет единица. А это значит, что существует какое-то другое число, которое еще не включено в список простых чисел. Следовательно, наше допущение не верно, и это множество не может иметь предела. Помимо доказательства Евклида, существует более современная формула, данная швейцарским математиком восемнадцатого века Леонардом Эйлером. Согласно ему, сумма, обратная сумме первых n чисел растет неограниченно с ростом числа n. А вот формула теоремы относительно распределения простых чисел: (n) растёт, как n/ln (n).
Какое наибольшее простое число?
Все тот же Леонард Эйлер смог найти самое большое для своего времени простое число. Это 231 – 1 = 2147483647. Однако к 2013 году было вычислено другое наиболее точное самое большое в списке простых чисел – 257885161 – 1. Его называют числом Мерсенна. Оно содержит около 17 миллионов десятичных цифр. Как видите, число, найденное ученым из восемнадцатого века, в несколько раз меньше этого. Так и должно было быть, ведь Эйлер вел данный подсчет вручную, нашему же современнику наверняка помогала вычислительная машина. Более того, это число было получено на факультете математики в одном из американских факультетов. Числа, названные в честь этого ученого, проходят через тест простоты Люка-Лемера. Однако наука не желает останавливаться на достигнутом. Фонд Электронных рубежей, который был основан в 1990 году в Соединенных Штатах Америки (EFF), назначил за нахождение больших простых чисел денежную награду. И если до 2013 года приз полагался тем ученным, которые найдут их из числа 1 и 10 миллионов десятичных чисел, то сегодня это цифра достигла от 100 миллионов до 1 миллиарда. Размер призов составляет от 150 до 250 тысяч долларов США.
Названия специальных простых чисел
Те числа, которые были найдены благодаря алгоритмам, созданным теми или иными учеными, и прошли тест простоты, называются специальными. Вот некоторые из них:
1. Мерссена.
2. Вудаа.
3. Ферма.
4. Каллена.
5. Прота.
6. Миллса и др.
Простота этих чисел, названных в честь вышеперечисленных ученых, устанавливается с использованием следующих тестов:
1. Люка-Лемера.
2. Пепина.
3. Ризеля.
4. Биллхарта – Лемера – Селфриджа и др.
Современная наука не останавливается на достигнутом, и, вероятно, в ближайшем будущем мир узнает имена тех, кто смог получить приз в 250.000 долларов, найдя наибольшее простое число.
syl.ru
Случайное простое число
В криптографии под случайным простым числом понимается простое число, содержащее в двоичной записи заданное количество битов k {\displaystyle k} , на алгоритм генерации которого накладываются определенные ограничения. Получение случайных простых чисел является неотъемлемой частью процедур выработки ключей во многих криптографических алгоритмах, включая RSA и ElGamal.
Ввиду того, что тестирование простоты больших чисел требует существенных временных затрат, требование простоты получаемого числа часто ослабляют до сильной псевдопростоты по нескольким различным случайным основаниям. Существующие алгоритмы тестирования сильной псевдопростоты на порядки быстрее лучших известных алгоритмов тестирования простоты. В то же время, числа, успешно прошедшие тестирования сильной псевдопростоты по нескольким случайным основаниям, с большой вероятностью являются простыми, причём эта вероятность растет с ростом количества оснований, по которым проводится тестирование.
Требования к алгоритму и его реализации
Требования к алгоритмам генерации случайных простых чисел сводятся к следующим двум:
- Распределение получаемых простых чисел должно быть близко к равномерному на множестве всех k-битных простых чисел. Существует несколько способов обеспечить выполнимость этого требования.
- Процесс генерации конкретного случайного простого числа нельзя воспроизвести, даже зная детали алгоритма и его реализации. Обычно выполнение этого требования обеспечивается использованием криптостойкого ГПСЧ, проинициализированного некоторым ключом, получаемым извне (т. е. не являющимся частью алгоритма или его реализации). В качестве ключа может выступать, например, значение криптографической хеш-функции от секретной фразы, запрашиваемой у пользователя.
Типовые алгоритмы генерации случайных простых чисел
Везде далее предполагается использование криптографически стойкого ГПСЧ, проинициализированного с помощью секретного ключа (детали зависят от используемого ГПСЧ и способа получения и представления ключа).
Тестирование простоты
Основная статья: Тест простотыПроверить (вероятную) простоту числа p, содержащего k битов, можно так:
- Убедиться, что p не делится на небольшие простые числа 3, 5, 7, 11, и т.д. до некоторого небольшого предела (например, 256). Такая проверка позволяет эффективно отсечь множество заведомо составных чисел, прежде чем проверять их посредством более трудоёмких алгоритмов. Так, проверка делимости p на простые числа 2, 3, 5 и 7 отсеивает все четные числа и 54% нечетных чисел, проверка делимости p на все простые числа до 100 отсеивает 76% нечетных чисел, а проверка делимости p на все простые числа до 256 отсеивает 80% нечетных чисел.
- Выполнить тест Миллера — Рабина с количеством раундов не меньше k.
Если число p не проходит хотя бы одной проверки — оно не является простым. В противном случае с большой вероятностью (зависящей от количества раундов) число p является простым.
Прямое построение
- Сгенерировать k − 1 {\displaystyle k-1} случайных битов и составить из них k-битное число p со старшим битом равным 1.
- Увеличить p на 1 и проверить его простоту. Повторять этот шаг до тех пор, пока не будет найдено простое число.
Второй шаг можно ускорить, если рассматривать только нечетные числа или числа сравнимые с 1 и 5 по модулю 6 и т.п.
(n—1)-методы
(n—1)-методы построения простых чисел используют знание о простых делителях числа n—1 для тестирования простоты n с помощью теста простоты Люка.[1]
Типичный представитель этого класса методов описан в книге «Введение в криптографию» под редакцией В. В. Ященко.[2]
Генерация простых чисел Софи Жермен
Простые числа Софи Жермен — такие простые p, что 2p + 1 тоже простое.
ru.wikipedia.org
Что такое простые числа?
Кто- нибудь может подсказать что это? Только, пожалуйста, без ссылок на википедию. Нужно очень простым языком. Спасибо!
Девушка бонда
Простое число, целое положительное число, большее, чем единица, не имеющее других делителей, кроме самого себя и единицы: 2, 3, 5, 7, 11, 13,...Понятие П. ч. является основным при изучении делимости натуральных (целых положительных) чисел; именно, основная теорема теории делимости устанавливает, что всякое целое положительное число, кроме 1, единственным образом разлагается в произведении П. ч. (порядок сомножителей при этом не принимается во внимание) . П. ч. бесконечно много (это предложение было известно ещё древнегреческим математикам, его доказательство имеется в 9-й книге "Начал" Евклида) . Вопросы делимости натуральных чисел, а следовательно, вопросы, связанные с П. ч. , имеют важное значение при изучении групп; в частности, строение группы с конечным числом элементов тесно связано с тем, каким образом это число элементов (порядок группы) разлагается на простые множители. В теории алгебраических чисел рассматриваются вопросы делимости целых алгебраических чисел; понятия П. ч. оказалось недостаточным для построения теории делимости — это привело к созданию понятия идеала. П. Г. Л. Дирихле в 1837 установил, что в арифметической прогрессии а + bx при х = 1, 2,...с целыми взаимно простыми а и b содержится бесконечно много П. ч.
Пчелинцева нина
Просто́е число́ — натуральное (целое положительное) число, имеющее ровно два различных натуральных делителя [1] — единицу и самого себя. Другими словами, число p является простым, если оно больше 1 и при этом делится без остатка только на 1 и на p (на самого себя).
Пример: 5 простое число, потому что делится только на 1 и на 5, а 6 является составным числом, так как делится на 2 и 3, помимо 1 и 6.
Натуральные числа, бо́льшие единицы, не являющиеся простыми, называются составными. Таким образом, все натуральные числа разбиваются на три класса: единицу (имеющую один натуральный делитель), простые числа (имеющие два натуральных делителя) и составные числа (имеющие больше двух натуральных делителей). Изучением свойств простых чисел занимается теория чисел. В теории колец простым числам соответствуют неприводимые элементы.
Как определить является ли число простым?
Дева вирджиния
Если число, как Анна20064 уже ответила, не делится ни на что, кроме единицы и самого себя, то оно простое. А определить кратность можно так:
если оканчивается на чётную цифру - чётное;
на 3 делится, если сумма его цифр делится на 3;
на 4 - если 2 последние цифры - нули, или составляют число, делящееся на 4;
на 5 - если оканчивается на 0 или 5;
на 6 - если делится и на 2, и на 3;
на 7 - если утроенное число десятков, сложенное с числом единиц, делится на 7;
на 8 - если число, образованное тремя последними цифрами, делится на 8, а если речь о трёхзначном - если число единиц, сложенное с удвоенным числом десятков и учетверённым числом сотен, делится на 8;
на 9 -если сумма его цифр делится на 9;
на 10 - если оно оканчивается на 0 (на 100 - если на два нуля и т. д.).
Источник - Википедия.
Анна20064
Число является простым, если оно ни на что не делится, кроме единицы и самого себя.
нужно проверить кратность (то есть делится ли) на 2,3,5,7,11,13 и так далее... По сути дела нужно делить на ряд простых чисел, верхний предел - в два раза меньше проверяемого числа - точно не ошибетесь.
Начитанный даг
Вот я всего лишь процитирую ответ автора, дабы не повторять одну и ту же простую истину. Мы лично проходили закон о простых числах по математике в пятом классе и до сих пор помню этот закон и всегда при определении простых чисел я знаю что:

bolshoyvopros.ru
Читайте также
- Определение числа дыхательных движений алгоритм
![Определение кислотного числа Определение кислотного числа]() Определение кислотного числа
Определение кислотного числа![Автомобиль определение Автомобиль определение]() Автомобиль определение
Автомобиль определение- Актив определение
![Вопросы определения Вопросы определения]() Вопросы определения
Вопросы определения![Бетон определение Бетон определение]() Бетон определение
Бетон определение![Болезнь определение Болезнь определение]() Болезнь определение
Болезнь определение![Власть определение Власть определение]() Власть определение
Власть определение![Выберите один из вариантов определения бытия Выберите один из вариантов определения бытия]() Выберите один из вариантов определения бытия
Выберите один из вариантов определения бытия![Газоопасные работы определение Газоопасные работы определение]() Газоопасные работы определение
Газоопасные работы определение- Выберите один из вариантов определения истины это
![Вихревое электрическое поле определение Вихревое электрическое поле определение]() Вихревое электрическое поле определение
Вихревое электрическое поле определение
 Определение кислотного числа
Определение кислотного числа Автомобиль определение
Автомобиль определение Вопросы определения
Вопросы определения Бетон определение
Бетон определение Болезнь определение
Болезнь определение Власть определение
Власть определение Выберите один из вариантов определения бытия
Выберите один из вариантов определения бытия Газоопасные работы определение
Газоопасные работы определение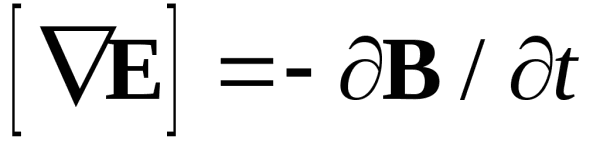 Вихревое электрическое поле определение
Вихревое электрическое поле определение