Среднее арифметическое
У этого термина существуют и другие значения, см. среднее значение.Сре́днее арифмети́ческое (в математике и статистике) множества чисел — сумма всех чисел, делённая на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ {\displaystyle {\bar {x}}} , произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и x ¯ {\displaystyle {\bar {x}}} в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда x ¯ {\displaystyle {\bar {x}}} (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + ⋯ + x n ) . {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\cdots +x_{n}).}Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры
- Для трёх чисел необходимо сложить их и разделить на 3:
- Для четырёх чисел необходимо сложить их и разделить на 4:
Или проще 5+5=10, 10:2. Потому что мы складывали 2 числа, а значит, сколько чисел складываем, на столько и делим.
Непрерывная случайная величина
Для непрерывно распределённой величины f ( x ) {\displaystyle f(x)} среднее арифметическое на отрезке [ a ; b ] {\displaystyle [a;b]} определяется через определённый интеграл:
f ( x ) ¯ [ a ; b ] = 1 b − a ∫ a b f ( x ) d x {\displaystyle {\overline {f(x)}}_{[a;b]}={\frac {1}{b-a}}\int _{a}^{b}f(x)dx}Некоторые проблемы применения среднего
Отсутствие робастности
Основная статья: Робастность в статистикеХотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Основная статья: Окупаемость инвестицийЕсли числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года всего на $5.1, средний рост в 8,2 % даёт конечный результат $35.1:
[$30 (1 — 0.1) (1 + 0.3) = $30 (1 + 0.082) (1 + 0.082) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: [$30 (1 + 0.1) (1 + 0.1) = $36.3].
Сложный процент в конце 2 года: 90 % * 130 % = 117 % , то есть общий прирост 17 %, а среднегодовой сложный процент 117 % ≈ 108.2 % {\displaystyle {\sqrt {117\%}}\approx 108.2\%} , то есть среднегодовой прирост 8,2 %.
Направления
Основная статья: Статистика направленийПри расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 1 ∘ + 359 ∘ 2 = {\displaystyle {\frac {1^{\circ }+359^{\circ }}{2}}=} 180°. Это число неверно по двум причинам.
- Во-первых, угловые меры определены только для диапазона от 0° до 360° (или от 0 до 2π при измерении в радианах). Таким образом, ту же пару чисел можно было бы записать как (1° и −1°) или как (1° и 719°). Средние значения каждой из пар будут отличаться: 1 ∘ + ( − 1 ∘ ) 2 = 0 ∘ {\displaystyle {\frac {1^{\circ }+(-1^{\circ })}{2}}=0^{\circ }} , 1 ∘ + 719 ∘ 2 = 360 ∘ {\displaystyle {\frac {1^{\circ }+719^{\circ }}{2}}=360^{\circ }} .
- Во-вторых, в данном случае, значение 0° (эквивалентное 360°) будет геометрически лучшим средним значеним, так как числа отклоняются от 0° меньше, чем от какого-либо другого значения (у значения 0° наименьшая дисперсия). Сравните:
- число 1° отклоняется от 0° всего на 1°;
- число 1° отклоняется от вычисленного среднего, равного 180°, на 179°.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
ru.wikipedia.org
Среднее арифметическое это:
Среднее арифметическое У этого термина существуют и другие значения, см. среднее значение.В математике и статистике сре́днее арифмети́ческое - одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их количество.
Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1] и является одной из наиболее распространенных мер центральной тенденции.
Частными случаями среднего арифметического являются генеральное среднее ( генеральной совокупности) и выборочное среднее ( выборки).
Содержание
|
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и в том, что μ является типичной ненаблюдаемой переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.
Примеры
- Для трёх чисел сложим их и поделим на 3:
- Для четырёх чисел сложим их и поделим на 4:
Непрерывная случайная величина
Для непрерывно распределённой величины среднее арифметическое на отрезке определяется через определённый интеграл:
Некоторые проблемы применения среднего
Отсутствие робастности
Основная статья: Робастность в статистикеХотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Основная статья: Окупаемость инвестицийЕсли числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего числа. Если акции в начале стоили $30 и упали на 10 %, они теперь стоят $27. Если акции выросли на 30 %, они теперь стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года на $5.1, средний рост в 8,2 % даёт конечный результат $35.1 [$30 (1 — 10 %) (1 + 30 %) = $30 (1 + 8,2 %) (1 + 8,2 %) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое увеличение [$30 (1 + 10 %) (1 + 10 %) = $36.3].
В общем, сложный процент даёт 90 % * 130 % = 117 % общий рост, а годовой прирост , то есть 8,2 % в год.
Направления
Основная статья: Статистика направленийОсобую осторожность нужно иметь при расчёте циклических данных, таких как фазы или углы. Наивное вычисление среднего арифметического 1° и 359° даёт результат 180°. Это неверно по двум причинам:
- Во-первых, угловые меры определены только до 360° (или 2π, при измерении в радианах). Таким образом, ту же пару можно записать 1° и −1°, или 1° и 719°, но каждая из которых даёт различные средние значения.
- Во-вторых, в этой ситуации, 0° (эквивалентно 360°) геометрически лучшее среднее значение: меньше дисперсия (обе точки на 1° от него, и на 179° от 180°, вычисленного среднего).
В целом применение такого рассмотрения средней величины ведёт к искусственному сдвигу его к середине числового диапазона. Решение этой проблемы заключается в использовании оптимальной формализации (а именно, определение среднего в качестве центральной точки, то есть точки, от которой наименьшая дисперсия), а также переопределение вычитания как модульного расстояния (то есть как расстояние от окружности; в частности, модульное расстояние между 1° и 359° — это 2°, а не 358°).
Примечания
- ↑ Cantrell, David W., "Pythagorean Means" from MathWorld
См. также
- Взвешенное среднее
- Винсоризованное среднее
- Гармоническое среднее
- Геометрическое среднее
- Медиана
- Мода
- Среднее Колмогорова
- Усеченное среднее
- Неравенство между средним арифметическим и средним геометрическим
- Неравенство Швейцера
Ссылки
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика
- Прикладная математика
статистика Статистический
вывод и
проверка
гипотез Корреляция
|
||||||||||||
|
||||||||||||
| Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания | ||||||||||||
| Линейные модели | Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ | |||||||||||
| Регрессия | Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия |
- Средние величины
Wikimedia Foundation. 2010.
dic.academic.ru
4.3. Средние величины. Сущность и значение средних величин
Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.
Например, обобщающим показателем доходов рабочих акционерного общества (АО) служит средний доход одного рабочего, определяемый отношением фонда заработной платы и выплат социального характера за рассматриваемый период (год, квартал, месяц) к численности рабочих АО.
Вычисление среднего - один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.
Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях.
Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве.
Средняя - это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает.
4.4. Виды средних и способы их вычисления
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется, одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д. Перечисленные средние относятся к классу степенных средних.
Помимо степенных средних в статистической практике используются средние структурные, в качестве которых рассматриваются мода и медиана.
Остановимся подробнее на степенных средних.
Средняя арифметическая
Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя, например: общий фонд заработной платы - это сумма заработных плат всех работников, валовый сбор урожая - сумма произведенной продукции со всей посевной площади.
Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.
Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой служит простая средняя.
Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):
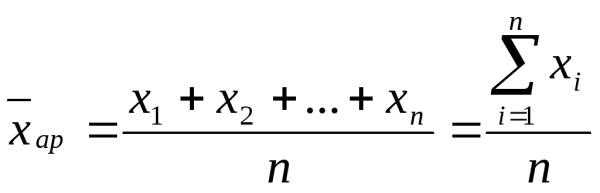 ,
,
где ![]() - индивидуальные значения варьирующего (варианты);м - число единиц совокупности.
- индивидуальные значения варьирующего (варианты);м - число единиц совокупности.
Далее пределы суммирования в формулах указываться не будут. Например, требуется найти среднюю выработку одного рабочего (слесаря), если известно, сколько деталей изготовил каждый из 15 рабочих, т.е. дан ряд индивидуальных значений признака, шт.:
21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.
Средняя арифметическая простая рассчитывается по формуле (4.1),1 шт.:
![]()
Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).
Средняя арифметическая взвешенная - средняя сгруппированных величин ![]() , - вычисляется по формуле:
, - вычисляется по формуле:
![]() , (4.2)
, (4.2)
где ![]() - веса (частоты повторения одинаковых признаков);
- веса (частоты повторения одинаковых признаков);
![]() - сумма произведений величины признаков на их частоты;
- сумма произведений величины признаков на их частоты;
![]() - общая численность единиц совокупности.
- общая численность единиц совокупности.
Технику вычисления средней арифметической взвешенной проиллюстрируем на рассмотренном выше примере. Для этого сгруппируем исходные данные и поместим их в табл. 4.1.
Таблица 4.1
Распределение рабочих по выработке деталей
|
Выработка деталей за смену одним рабочим, шт. |
Число рабочих |
xf |
|
18 19 20 21 22 |
2 4 5 3 1 |
36 76 100 63 22 |
|
Итого |
15 |
297 |
По формуле (4.2) средняя арифметическая взвешенная равна, шт.:
![]() .
.
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид:
![]()
где ![]() - частность, т.е. доля каждой частоты в общей сумме всех
- частность, т.е. доля каждой частоты в общей сумме всех
частот.
Если частоты подсчитывают в долях (коэффициентах), то ![]() = 1,и формула средней арифметически взвешенной имеет вид:
= 1,и формула средней арифметически взвешенной имеет вид:
![]()
Вычисление средней арифметической взвешенной из групповых средних ![]() осуществляется по формуле:
осуществляется по формуле:
![]() ,
,
где f -число единиц в каждой группе.
Результаты вычисления средней арифметической из групповых средних представлены в табл. 4.2.
Таблица 4.2
Распределение рабочих по среднему стажу работы
|
Номер цеха |
Средний стаж работы, лет ^гр |
Число рабочих, чел.f |
|
1-й 2-й 3-й |
5 7 10 |
90 60 50 |
|
Итого |
- |
200 |
В этом примере вариантами являются не индивидуальные данные о стаже работы отдельных рабочих, а средние по каждому цеху ![]() . Весами fявляются численности рабочих в цехах. Отсюда средний стаж работы рабочих по всему предприятию составит, лет:
. Весами fявляются численности рабочих в цехах. Отсюда средний стаж работы рабочих по всему предприятию составит, лет:
![]() .
.
Расчет средней арифметической в рядах распределения
Если значения осредняемого признака заданы в виде интервалов («от - до»), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд. Рассмотрим следующий пример (табл. 4.3).
От интервального ряда перейдем к дискретному путем замены интервальных значений их средними значениями/(простая средняя
Таблица 4.3
Распределение рабочих АО по уровню ежемесячной оплаты труда
в 2000 г.
|
Группы рабочих по |
Число рабочих, |
Середина интервала, |
xf |
|
оплате труда, руб. |
чел., f |
руб., х |
|
|
До 500 |
5 |
450 |
2250 |
|
500-600 |
15 |
550 |
8250 |
|
600-700 |
20 |
650 |
13000 |
|
700-800 |
30 |
750 |
22500 |
|
800-900 |
16 |
850 |
13600 |
|
900 и более |
14 |
950 |
13300 |
|
Итого |
100 |
- |
72900 |
величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним (второй и предпоследний).
При таком исчислении средней допускается некоторая неточность, поскольку делается предположение о равномерности распределения единиц признака внутри группы. Однако ошибка будет тем меньше, чем уже интервал и чем больше единиц в интервале.
После того как найдены середины интервалов, вычисления делают так же, как и в дискретном ряду, - варианты умножают на частоты (веса) и сумму произведений делят на сумму частот (весов), тыс. руб.:
![]() .
.
Итак, средний уровень оплаты труда рабочих АО составляет 729 руб. в месяц.
Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчета средней можно упростить и облегчить, если воспользоваться ее свойствами. Приведем (без доказательства) некоторые основные свойства средней арифметической.
Свойство 1. Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в iраз, то среднее значение нового признака соответственно уменьшится или увеличится в iраз.
Свойство 2. Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А.
Свойство 3. Если веса всех осредняемых вариантов уменьшить или увеличить в к раз, то средняя арифметическая не изменится.
В качестве весов средней вместо абсолютных показателей можно использовать удельные веса в общем итоге (доли или проценты). Тем самым достигается упрощение расчетов средней.
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается, когда в качестве А выбирается значение одного из центральных вариантов, обладающего наибольшей частотой, в качестве / - величина интервала (для рядов с одинаковыми интервалами). Величина Л называется началом отсчета, поэтому такой метод вычисления средней называется «способом отсчета от условного нуля» или «способом моментов».
Допустим, что все варианты х сначала уменьшены на одно и то же число А, а затем уменьшены в iраз. Получим новый вариационный ряд распределения новых вариантов ![]() .
.
Тогда новые варианты будут выражаться:
![]() ,
,
а их новая средняя арифметическая ![]() , -момент первого порядка -формулой:
, -момент первого порядка -формулой:
![]() .
.
Она равна средней из первоначальных вариантов, уменьшенной сначала на А, а затем в iраз.
Для получения действительной средней надо момент первого порядка m1, умножить на iи прибавить А:
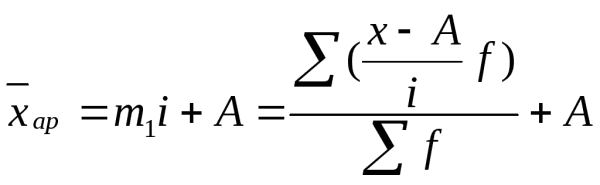 .
.
Данный способ вычисления средней арифметической из вариационного ряда называют «способом моментов». Применяется этот способ в рядах с равными интервалами.
Расчет средней арифметической по способу моментов иллюстрируется данными табл. 4.4.
Таблица 4.4
Распределение малых предприятий региона по стоимости основных производственных фондов (ОПФ) в 2000 г.
|
Группы предприятий по стоимости ОПФ, тыс. руб. |
Число предприятий,f |
Середины интервалов, x |
|
|
|
14-16 16-18 18-20 20-22 22-24 |
2 6 10 4 3 |
15 17 |
-2 -1 0 1 2 |
-4 -6 0 4 6 |
|
19 |
||||
|
21 22 |
||||
|
Итого |
25 |
- |
- |
0 |
Находим момент первого порядка
![]() .
.
Затем, принимая А = 19 и зная, что i= 2, вычисляем х, тыс. руб.:
![]()
StudFiles.ru
Что такое среднее арифметическое? Как найти среднее арифметическое?
Формула среднего арифметического чисел?
Алекс-89
Среднее арифметическое нескольких чисел — это сумма этих чисел, делённая на их количество.
x ср = S/n
где:
x ср — среднее арифметическое
S — сумма чисел
n — количество чисел.
Например, нам нужно найти среднее арифметическое чисел 3, 4, 5 и 6.
Для этого нам нужно их сложить и полученную сумму разделить на 4:
(3 + 4 + 5 + 6) : 4 = 18 : 4 = 4,5.
Алсу - ш
Мне, как математику, интересны вопросы по данному предмету.
Начну с истории вопроса. Над средними величинами задумывались с древних времмен. Среднее арифметическое, среднее геометоическое, среднее гармоническое. Эти понятия предложены в древней Греции пифагорийцами.
А теперь интересующий нас вопрос. Что же понимается под средним арифметичским нескольких чисел:

Итак, для нахождения среднего арифметического чисел нужно прибавить все числа и разделить полученную сумму на количество слагаемых.
Имеет место формула:
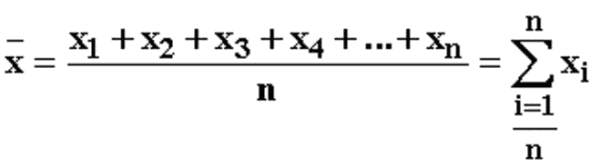
Пример. Найти среднее арифметическое чисел: 100, 175, 325.
Решение.
Воспользуемся формулой нахождения среднего арифметического трех чисел (то есть вместо n будет 3; нужно сложить все 3 числа и разделить полученную сумму на их количество, т.е. на 3). Имеем: х=(100+175+325)/3=600/3=200.
Ответ: 200.
Lady v
Арифметика считается самым элементарным разделом математики и изучает простые действия с числами. Поэтому и среднее арифметическое также находится очень просто. Начнем с определения. Среднее арифметическое - это величина, которая показывает какое число наиболее близко к истине при нескольких последовательных однотипных действиях. Например при беге на сто метров человек каждый раз показывает разное время, но средняя величина будет в пределах например 12 секунд. Нахождение среднего арифметического таким образом сводится в последовательному суммированию всех чисел определенного ряда (результатов забегов) и деление этой суммы на количество этих забегов (попыток, чисел). В виде формулы это выглядит так:
Sариф = (Х1+Х2+..+Хn)/n
Mb78
Среднее арифметическое - это среднее число между несколькими числами.
Например между числами 2 и 4 среднее число 3.
Формула нахождения среднего арифметического такая:
Нужно сложить все числа и разделить на количество этих чисел:
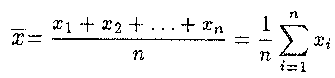
Например у нас 3 числа: 2, 5 и 8.
Находим среднее арифметическое:
X=(2+5+8)/3=15/3=5
Область применения среднего арифметического достаточно широка.
Например можно зная координаты двух точек отрезка найти координаты середины этого отрезка.
Например координаты отрезка: (X1,Y1,Z1)-(X2,Y2,Z2).
Обозначим середину этого отрезка координатами X3,Y3,Z3.
Отдельно находим середину для каждой координаты:
X3=(X1+X2)/2;
Y3=(Y1+Y2)/2;
Z3=(Z1+Z2)/2;
Красивая поляна
Средне арифметическое число, это числа сложенные вместе и деленные на их количество, полученный ответ и есть средне арифметическое число.
Например: Катя положила в копилку 50 рублей, Максим 100 рублей, а Саша положил в копилку 150 рублей. 50 + 100 + 150 = 300 рублей в копилке, теперь делим эту сумму на три (три человека положили деньги). Итак 300 : 3 = 100 рублей. Эти 100 рублей и будет средне арифметически, каждый из них положил в копилку.
Есть такой простой пример: один человек ест мясо, другой человек ест капусту, а средне арифметически они оба едят голубцы.
Таким же образом рассчитывают среднюю зарплату...
Simpl
Среднеарифметическое-это среднее значение из заданных...
Т.е. по простому имеем количество палочек разной длины и хотим узнать их среднее значение..
Логично, что для этого мы их сводим вместе, получая длинную палку, а потом делим её на требуемое число частей..
Вот и выходит среднеарифметическое..
Вот так и выводится формула:Sa=(S(1)+..S(n))/n..
Птичка2014
Среднее арифметическое - это сумма всех значений и деленное на их количество.
Например числа 2, 3 , 5, 6 . Нужно их сложить 2+ 3+ 5 + 6 = 16
16 делим на 4 и получаем ответ 4 .
4 и есть среднее арифметическое этих чисел.
Azamatik
Средним арифметическим называют сумму чисел, разделенное на количество этих самых чисел. А найти среднее арифметическое очень просто.
Как следует из определения мы должны взять числа, сложить их и разделить на их количество.
Приведем пример: дается числа 1, 3, 5, 7 и нам надо найти среднее арифметическое этих чисел.
- сначала складываем эти числа (1+3+5+7) и получаем 16
- полученный результат нам надо разделить на 4 (кол - во): 16/4 и получаем результат 4.
Итак, среднее арифметическое чисел 1, 3, 5 и 7 - это 4.
Tana76
Среднее арифметическое - среднее значение среди заданных показателей.
Оно находится путем деления суммы всех показателей на их количество.
Например, у меня есть 5 яблок весом 200, 250, 180, 220 и 230 грамм.
Средний вес 1 яблока находим так:
- ищем общий вес всех яблок (сумму всех показателей) - он равен 1080 граммов,
- делим общий вес на количество яблок 1080:5 = 216 граммов. Это и есть среднее арифметическое.
Это наиболее часто применяемый в статистике показатель.
Зеленый чебуречек
Это мы знаем со школьной скамьи. У кого был хороший учитель по математике, то запомнить это нехитрое действие можно было с первого раза.
При нахождении среднего арифметического необходимо сложить все имеющиеся числа и разделить на их количество.
Например, я купила в магазине 1 кг яблок, 2 кг бананов, 3 кг апельсинов и 1 кг киви. Сколько килограммов в среднем я купила фруктов.
1+2+3+1=7.
7/4= 1,8 килограммов. Это и будет среднеарифметическим значением.
Бьемон эпу
Помню как итоговую контрольную по математике сдавал
Так там нужно было среднее арифметическое найти.
Хорошо что добрые люди подсказали что делать, иначе беда.
Например у нас 4 числа.
Складываем числа и делим на их количество (в данном случае 4)
Например цифры 2,6,1,1. Складываем 2+6+1+1 и делим на 4 = 2.5
Как видите ничего сложного. Так что среднее арифметическая - это среднее значение всех чисел.
bolshoyvopros.ru
Как найти среднее арифметическое чисел 42,5;41,7;40,9;43,1;42,3.
Максим ю. Волков
В математике и статистике сре́днее арифмети́ческое (или просто среднее) набора чисел — это сумма всех чисел в этом наборе, делённая на их количество.
Среднее арифметическое является наиболее общим и самым распространённым понятием средней величины. Термин "среднее арифметическое" предпочитают в математике и статистике, чтобы отличать его от других средних величин, таких как медиана и мода. Частными случаями среднего арифметического являются генеральное среднее (генеральной совокупности) и выборочное среднее (выборки) .
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений» . Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего» , а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу) . Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода) . Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа» , то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Наталья зубченко
В математике и статистике сре́днее арифмети́ческое (или просто среднее) набора чисел — это сумма всех чисел в этом наборе, делённая на их количество.
Среднее арифметическое является наиболее общим и самым распространённым понятием средней величины. Термин "среднее арифметическое" предпочитают в математике и статистике, чтобы отличать его от других средних величин, таких как медиана и мода. Частными случаями среднего арифметического являются генеральное среднее (генеральной совокупности) и выборочное среднее (выборки) .
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений» . Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего» , а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу) . Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода) . Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа» , то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Читайте также
![Среднее значение Среднее значение]() Среднее значение
Среднее значение![Расчет среднего значения Расчет среднего значения]() Расчет среднего значения
Расчет среднего значения![Сущность и значение средних величин Сущность и значение средних величин]() Сущность и значение средних величин
Сущность и значение средних величин![Символ среднего значения Символ среднего значения]() Символ среднего значения
Символ среднего значения![Среднее значение функции на отрезке Среднее значение функции на отрезке]() Среднее значение функции на отрезке
Среднее значение функции на отрезке![Обозначение среднего значения Обозначение среднего значения]() Обозначение среднего значения
Обозначение среднего значения![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![1515 На часах значение 1515 На часах значение]() 1515 На часах значение
1515 На часах значение![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия![16 16 Значение времени 16 16 Значение времени]() 16 16 Значение времени
16 16 Значение времени![Семен значение имени характер и судьба Семен значение имени характер и судьба]() Семен значение имени характер и судьба
Семен значение имени характер и судьба
 Среднее значение
Среднее значение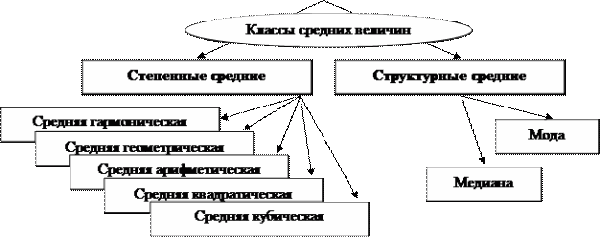 Расчет среднего значения
Расчет среднего значения Сущность и значение средних величин
Сущность и значение средних величин Символ среднего значения
Символ среднего значения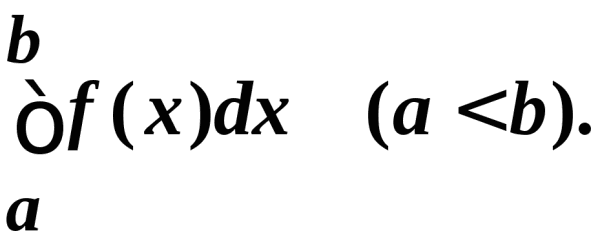 Среднее значение функции на отрезке
Среднее значение функции на отрезке Аутентичность значение слова
Аутентичность значение слова 1515 На часах значение
1515 На часах значение Чувак значение слова с еврейского
Чувак значение слова с еврейского Барыга значение слова википедия
Барыга значение слова википедия 16 16 Значение времени
16 16 Значение времени Семен значение имени характер и судьба
Семен значение имени характер и судьба