8.3. Свойства определенного интеграла Римана
![]()
-

 .
. -
Линейность. Если f(x), g(x) интегрируемs на [a, b], то
 (следует из линейности суммы и предельного перехода)
(следует из линейности суммы и предельного перехода) -
Аддитивность. Если f(x) интегрируема на [a, b] и
с(a, b), то![]()
Доказательство. Рассмотрим такие разбиения отрезка [a, b], где одной из точек xi является точка с. ![]()
При 0![]()
-
Если f(x) интегрируема на [a,b] иf1(x) =f(x) для всехx[a;b] за исключением конечного числа точек, то

(интеграл Римана не замечает изменения функции в конечном числе точек).
Доказательство. Изменяя f(x) в конечном числе точек, в интегральной сумме изменим конечное число слагаемых, но при 0 их вклад в сумму стремится к нулю (так как f(x) ограничена).
Свойства, связанные с оценкой интеграла с помощью неравенств (функцииf(x) и g(x) интегрируемы на [a, b]):
-

-
 .
. -


-
 .
. -
 .
.
Доказательство. Исходим из определения:![]() .
.
Свойство5.1. очевидно, так как при a< b множители xiположительны. Предельный переход сохраняет неравенство:![]()
5.2 следует из 5.1. и линейности интеграла:
![]()
![]() .5.3.
.5.3.
![]()
![]() .
.
5.4. ![]()
![]() ;
;
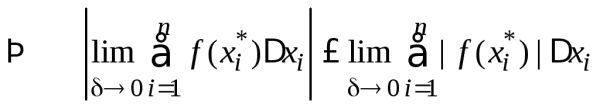
(использовалась непрерывность модуля) 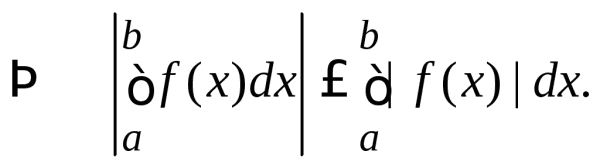 .
.
5.5. ![]() .
.
Замечание 1. Свойства 2, 3 и 4 остаются справедливыми и при a > b, при этом с(b,a).
Замечание 2. Свойство 3 можно формулировать при любом взаимном расположении точек a, b, c, если функция интегрируема на большем промежутке.
Н![]() апример,
апример,
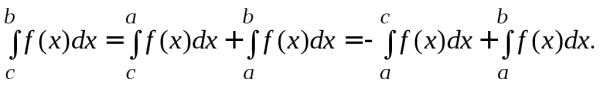
![]()
Замечание 3. Свойства 5 при a> bперестают быть верными.
Можно переформулировать. Например, (5.5):
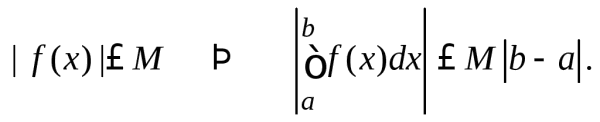
12. Среднее значение интегрируемой функции на отрезке. Теорема о среднем значении для интеграла Римана. (8.4)
8.4. Теорема о среднем значении.
Определение.Число fср= ![]() называетсясредним значением интегрируемой функции f(x) на отрезке [a, b].
называетсясредним значением интегрируемой функции f(x) на отрезке [a, b].
Теорема.Если f(x) непрерывна на [a, b], то в некоторой точке с этого отрезка она принимает свое среднее значение: с[a, b]: f(c) =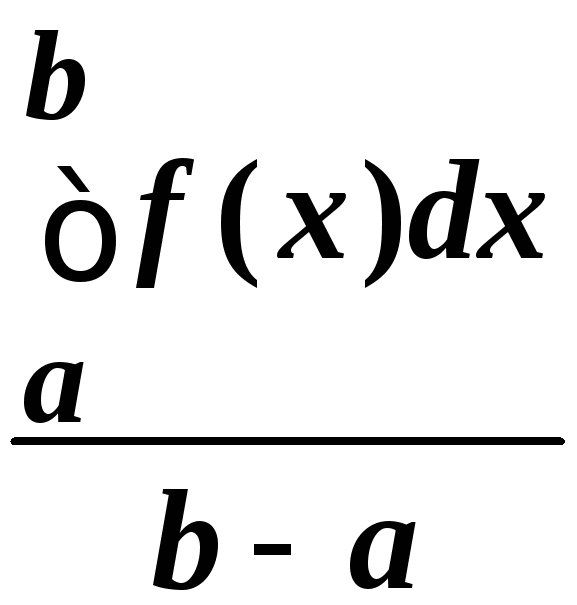 или
или 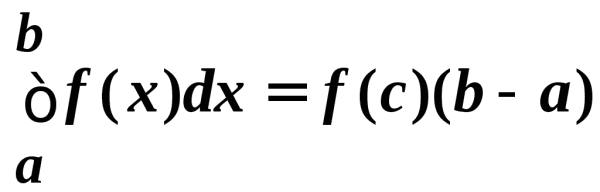 .
.
Доказательство. Значения непрерывной функции на отрезке [a, b] образуют отрезок [m, M], где m и M наименьшее и наибольшее значения.
По свойству 5.3![]()
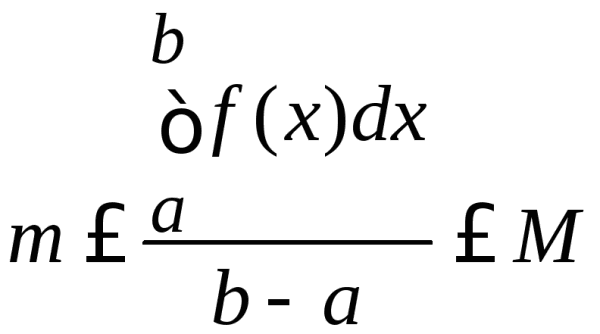 т.е.fср[m, M].
т.е.fср[m, M].
это промежуточное значение принимается функцией в некоторой точке отрезка.
Замечание. Разрывная интегрируемая функция может не принимать свое среднее значение ни в одной точке отрезка.
Пример.![]()
Вычислим среднее значение.
![]() =
=  ;
;
fср=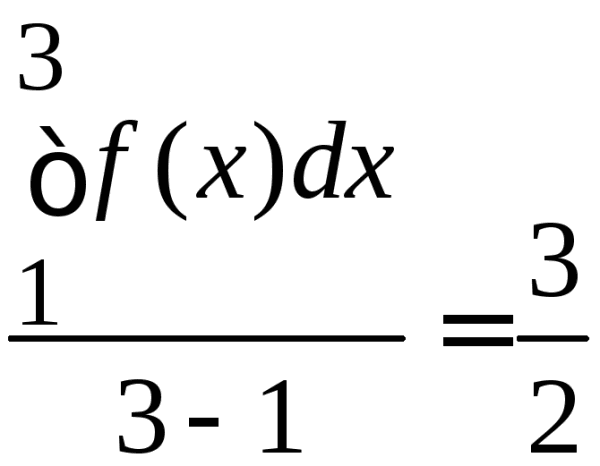 .
.
На отрезке [1, 3] среднее значение не принимается ни в одной точке.
13. Свойства определенного интеграла как функции верхнего предела: непрерывность. (8.5)
8.5. Интеграл Римана с переменным верхним пределом. Доказательство существования первообразной у непрерывной функции. Формула Ньютона-Лейбница.
Пусть f(x) задана на интервале (c, d) и интегрируема на каждом отрезке, содержащемся в этом интервале.
Выберем точку а(c, d) и рассмотрим функцию![]() (интеграл Римана с переменным верхним пределом).xопределена на всем интервале (c, d).
(интеграл Римана с переменным верхним пределом).xопределена на всем интервале (c, d).
Теорема 1.Для любой интегрируемой f(x)функция x непрерывна.
Доказательство. Рассмотрим точку x(c, d). Интегрируемая функция ограничена в некоторой окрестности точки x: MR xU(x) |f(x)| M.
xx+ x–x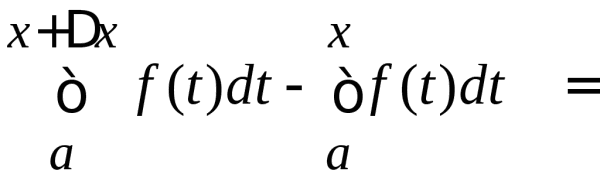 =
=![]() .|x| = -=
.|x| = -=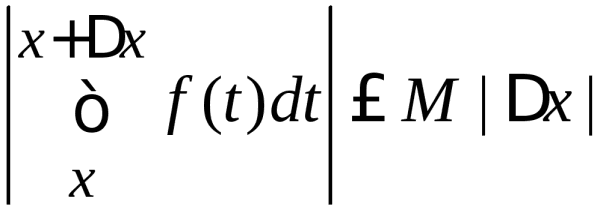 .
.
При x0 имеем 0, что и означает непрерывность x в т. x(c, d).
Теорема 2 (о существовании первообразной у непрерывной функции). Для любой непрерывной f(x)на интервале (c, d) функция x дифференцируема на (c, d) и является первообразной для f(x), т. е.![]()
Доказательство.
 [применим теорему о среднем значении]
[применим теорему о среднем значении]
![]() .
.
Но т. с заключена между x и x+x, поэтому при x0 имеем сx и в силу непрерывности функции f(x). Итак, ![]()
Теорема 3. Формула Ньютона-Лейбница.
Если f(x)непрерывна на [a, b], то ![]()
где F(x) – любая первообразная для f(x).
Другая форма записи:![]()
Доказательство. Пусть F(x) – известная первообразная для f(x) на [a, b].
Еще одна первообразная: ![]() (x) – F(x) = const:
(x) – F(x) = const:
![]() .
.
x = a ![]()
![]() .
.
x = b ![]() .
.
StudFiles.ru
Среднее значение функции это:
Среднее значение функции У этого термина существуют и другие значения, см. среднее значение.Среднее значение функции — это некоторое число, заключённое между наименьшим и наибольшим её значениями. В дифференциальном и интегральном исчислении имеется ряд «теорем о среднем», устанавливающих существование таких точек, в которых функция или её производная получает то или иное среднее значение. Наиболее важной теоремой о среднем значении функции в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если непрерывна на отрезке и дифференцируема в интервале , то существует точка , принадлежащая интервалу , такая, что . В интегральном исчислении наиболее важной теоремой о среднем значении является следующая: если непрерывна на отрезке , а сохраняет постоянный знак, то существует точка из интервала такая, что
В частности, если , то
Вследствие этого под средним значением функции на отрезке обычно понимают величину
Аналогично определяется среднее значение функции нескольких переменных в некоторой области.
См. также
- Средние Колмогорова
- Первая теорема о среднем
- Математическое ожидание
- Математический анализ
- Функции
Wikimedia Foundation. 2010.
dic.academic.ru
/ теория / 53 ВОПРОС
53.Условие интегрируемости функций. Основные свойства определенного интеграла.
Условия интегрируемости функции на отрезке ![]() – это условия существования определенного интеграла
– это условия существования определенного интеграла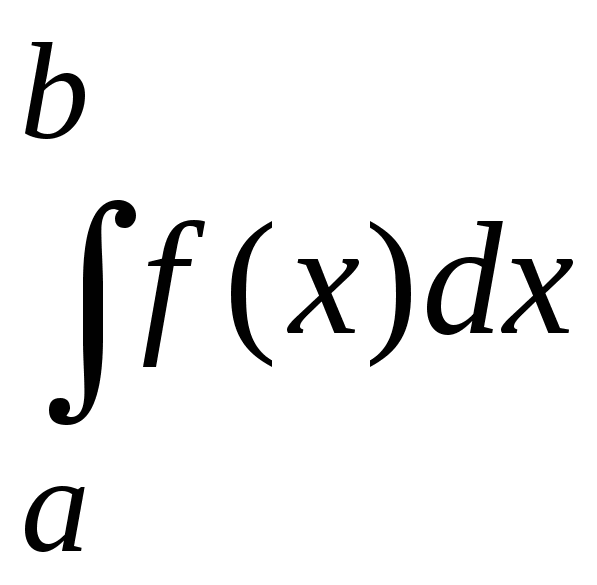 . При определении его как предела интегральной суммы предполагалось, что функция
. При определении его как предела интегральной суммы предполагалось, что функция![]() ограничена на отрезке
ограничена на отрезке![]() .
.
Необходимое условие интегрируемости функции
Покажем, что условие ограниченности функций на отрезке ![]() являетсянеобходимым условием интегрируемости функций, т.е. справедлива следующая теорема.
являетсянеобходимым условием интегрируемости функций, т.е. справедлива следующая теорема.
Т. Если ![]() существует, то функция
существует, то функция![]() ограничена на отрезке
ограничена на отрезке![]() .
.
Ограниченность является необходимым, но не достаточным условием интегрируемости функции на отрезке ![]() , Существуют ограниченные функции, не являющиеся интегрируемыми.
, Существуют ограниченные функции, не являющиеся интегрируемыми.
Достаточные условия интегрируемости функции
Т. Если функция ![]() непрерывна на отрезке [a, b], то она интегрируема на этом отрезке, т.е. существует
непрерывна на отрезке [a, b], то она интегрируема на этом отрезке, т.е. существует 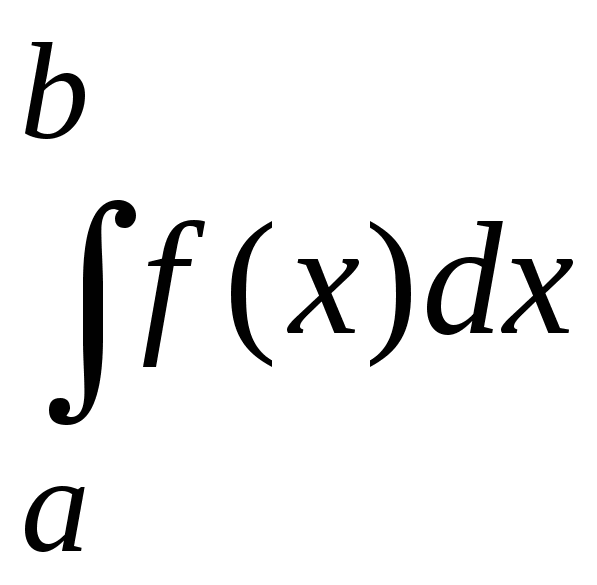
Т. Если функция ![]() ограничена на отрезке [a, b] и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
ограничена на отрезке [a, b] и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
Т. Если функция ![]() монотонна и ограничена на отрезке [a, b], то она интегрируема на [a, b].
монотонна и ограничена на отрезке [a, b], то она интегрируема на [a, b].
Свойства определенного интеграла, выражаемые равенствами
1. Если нижний и верхний пределы интегрирования равны ![]() ,то интеграл равен нулю:
,то интеграл равен нулю: ![]() .
.
2. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
![]()
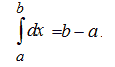
3.
4. Если функция f(x) интегрируема на отрезке [a, b], то и функция ![]() ,где k – постоянная, также интегрируема на [a, b], причем
,где k – постоянная, также интегрируема на [a, b], причем 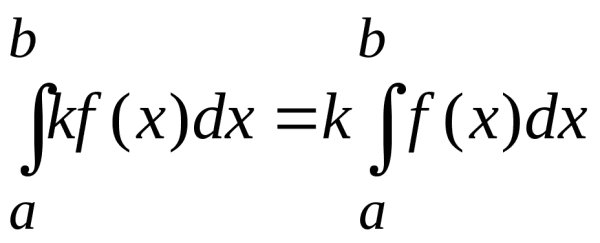
![]() ,
,
т.е. постоянный множитель можно выносить за знак определенного интеграла.
5. Если функции f(x) и g(x) интегрируемы на [a, b], то ![]() также интегрируема на [a, b], причем
также интегрируема на [a, b], причем
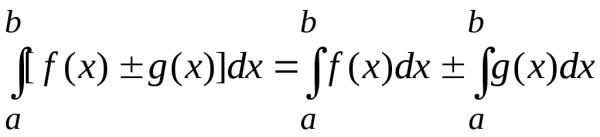 .
.
6. Аддитивность определенного интеграла. Если существуют интегралы 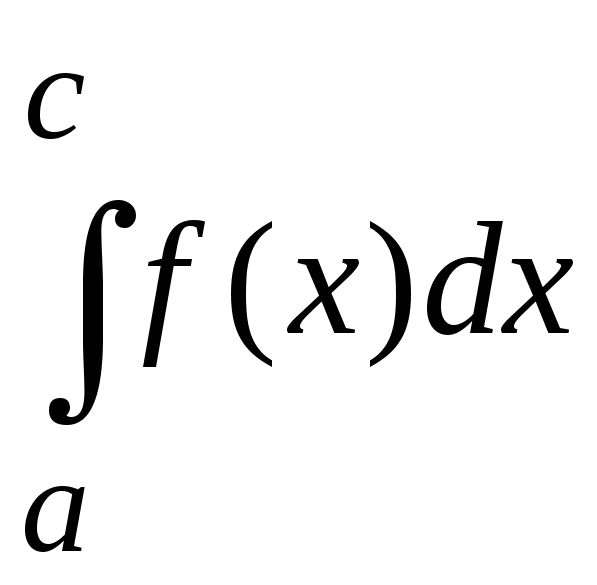 и
и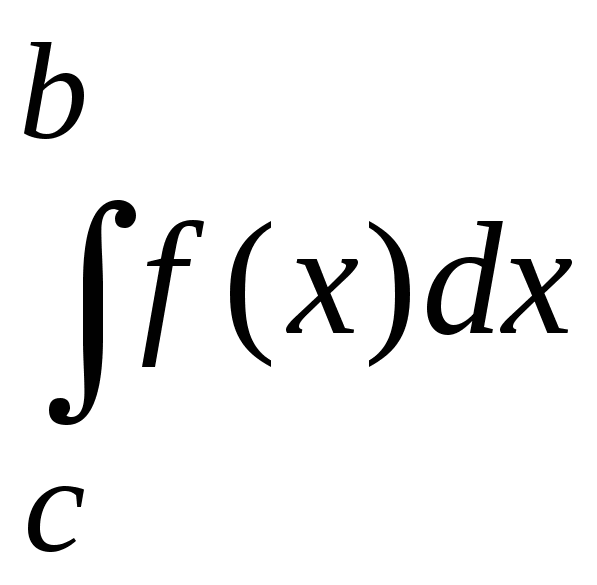 ,то существует также интеграл
,то существует также интеграл 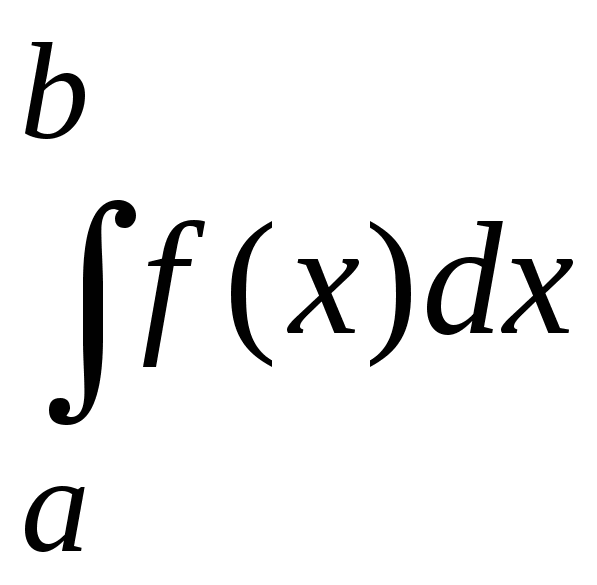 (и обратно)и для любых чисел a, b, c
(и обратно)и для любых чисел a, b, c  .
.
7. Если функция f(x) не меняет знак на ![]() ,то определенный интеграл
,то определенный интеграл 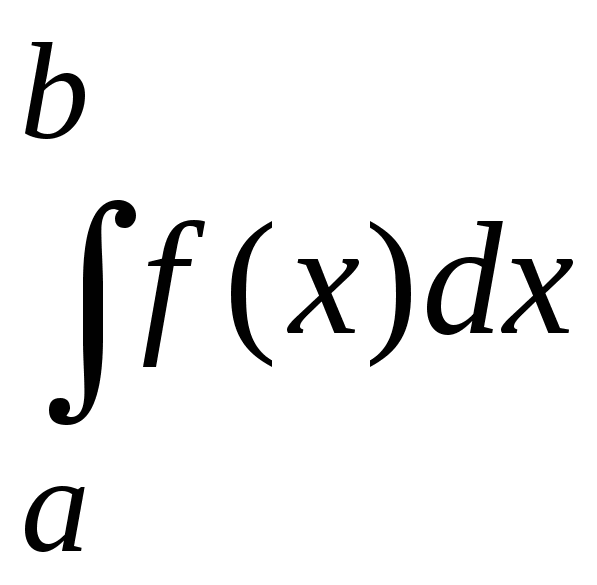 сохраняет ее знак, т.е. если
сохраняет ее знак, т.е. если ![]()
![]()
![]() ,то
,то  ,
,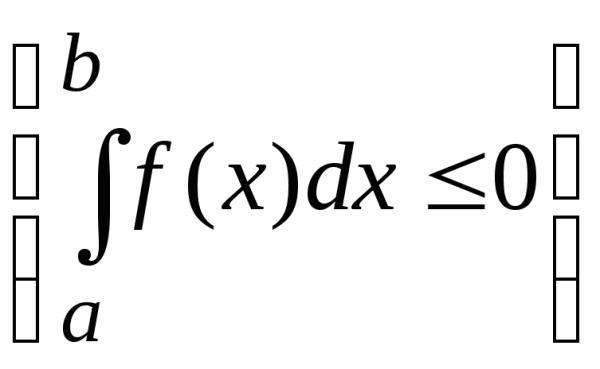 ,
,![]() .
.
8. Монотонность определенного интеграла. Если интегрируемые функции ![]() и
и![]() удовлетворяют неравенству
удовлетворяют неравенству![]()
![]() , то
, то 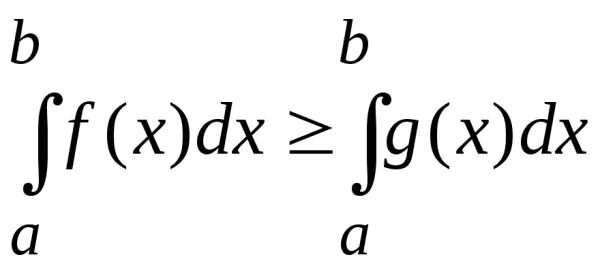 ,
,![]() .
.
9. Оценка интеграла. Если f(x) интегрируема на ![]()
![]() и
и![]()
![]() , то
, то ,
,![]() .
.
10. (о среднем значении для непрерывной функции). Если функция f(x) непрерывна на отрезке ![]() , то существует такая точка
, то существует такая точка ![]() ,что
,что 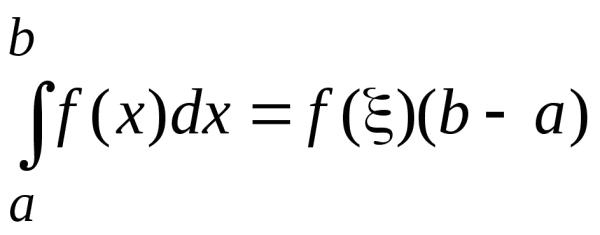 ,
,
т.е. определенный интеграл от непрерывной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ![]() отрезка интегрирования
отрезка интегрирования ![]() и длины b–a этого отрезка.
и длины b–a этого отрезка.
Число ![]() , определяемое по формуле
, определяемое по формуле 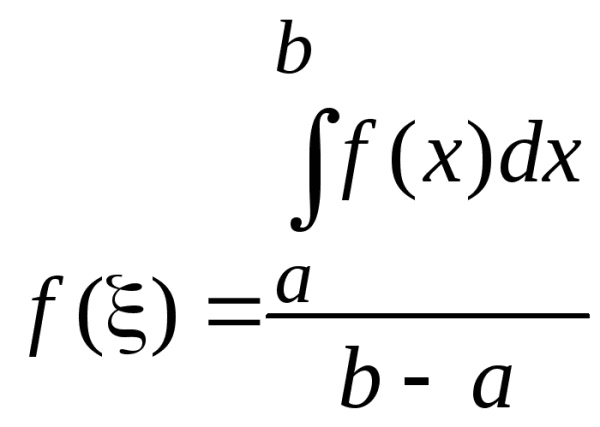 ,называется интегральным средним значением функции f(x) на отрезке
,называется интегральным средним значением функции f(x) на отрезке ![]() .
.
StudFiles.ru
Найти наименьшее значение функции на отрезке
Найти наименьшее значение функции на отрезке
f(x)=(1/4x^4)-(2*x^2)+1
Х [-1;3]
Мертвый_белый_снег
Как вообще ищется минимальное значение функции на отрезке: минимум функции на отрезке может достигаться 1) на концах отрезка; 2) в точках разрыва функции; 3) в точках эстремума.
1. Найдем точки, в которых может быть минимум: концы отрезка ---x=-1, x=3.
В точках экстремума производная равна нулю, поэтому их ищем из уравнения f'(x)=0:
f'(x)=x^3-4x=0
x=0 или x=+/-2 (-2 не входит в нужных нам отрезок, поэтому ее проверять не будем) .
Функция разрывов не имеет.
2. Проверяем значение функции в указанных точках:
f(-1)=1/4
f(0)=1
f(2)=-3
f(3)=5/4
Наименьшее значение ---(-3).
Все ок?
Читайте также
![Обозначение среднего значения Обозначение среднего значения]() Обозначение среднего значения
Обозначение среднего значения![Таблица значений интегральной функции лапласа Таблица значений интегральной функции лапласа]() Таблица значений интегральной функции лапласа
Таблица значений интегральной функции лапласа![Среднее значение Среднее значение]() Среднее значение
Среднее значение![Расчет среднего значения Расчет среднего значения]() Расчет среднего значения
Расчет среднего значения![Таблица значений функции Таблица значений функции]() Таблица значений функции
Таблица значений функции![Сущность и значение средних величин Сущность и значение средних величин]() Сущность и значение средних величин
Сущность и значение средних величин![Символ среднего значения Символ среднего значения]() Символ среднего значения
Символ среднего значения![Как найти область значения функции Как найти область значения функции]() Как найти область значения функции
Как найти область значения функции![Аутентичность значение слова Аутентичность значение слова]() Аутентичность значение слова
Аутентичность значение слова![1515 На часах значение 1515 На часах значение]() 1515 На часах значение
1515 На часах значение![Чувак значение слова с еврейского Чувак значение слова с еврейского]() Чувак значение слова с еврейского
Чувак значение слова с еврейского![Барыга значение слова википедия Барыга значение слова википедия]() Барыга значение слова википедия
Барыга значение слова википедия
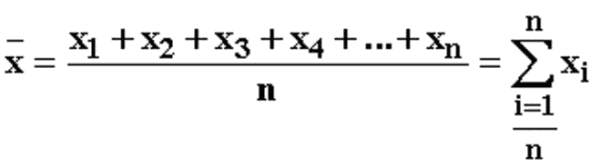 Обозначение среднего значения
Обозначение среднего значения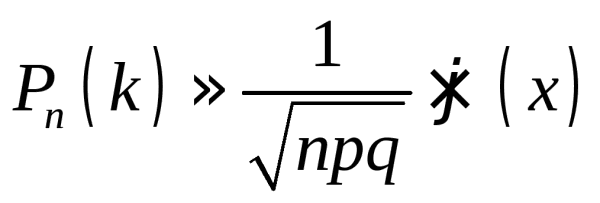 Таблица значений интегральной функции лапласа
Таблица значений интегральной функции лапласа Среднее значение
Среднее значение Расчет среднего значения
Расчет среднего значения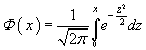 Таблица значений функции
Таблица значений функции Сущность и значение средних величин
Сущность и значение средних величин Символ среднего значения
Символ среднего значения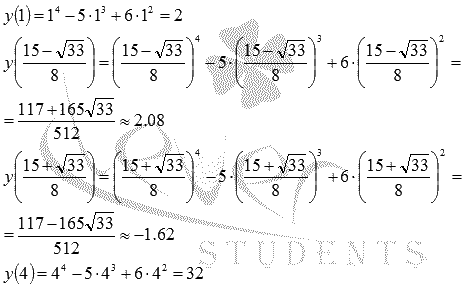 Как найти область значения функции
Как найти область значения функции Аутентичность значение слова
Аутентичность значение слова 1515 На часах значение
1515 На часах значение Чувак значение слова с еврейского
Чувак значение слова с еврейского Барыга значение слова википедия
Барыга значение слова википедия