Стереометрия основные понятия и определения

/ Основные понятия и аксиомы стереометрии

"Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей"

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Простейшие фигуры в пространстве: точка, прямая, плоскость.

Плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.

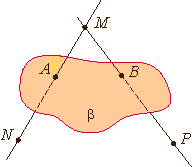
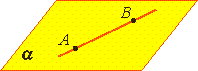
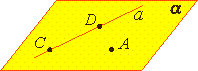
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,

Аксиомы стереометрии и их следствия

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
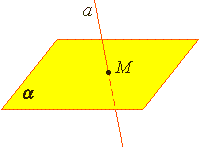
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
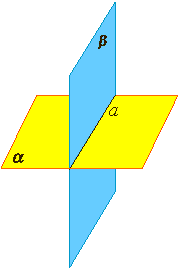
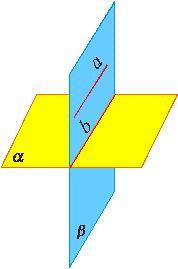
Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты.

Некоторые следствия из аксиом

Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
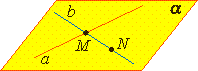
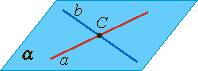
Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Параллельные прямые в пространстве

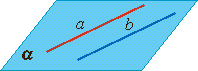
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема о параллельных прямых.

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

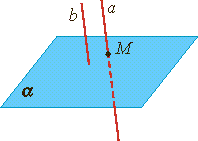
Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

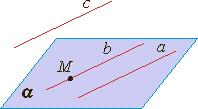
Теорема о трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).

Параллельность прямой и плоскости

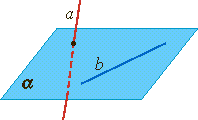
Прямая и плоскость называются параллельными, если они не имеют общих точек.

Признак параллельности прямой и плоскости

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Взаимное расположение прямых в пространстве


Пересекающиеся прямые: лежат в одной плоскости, имеют одну общую точку.	Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются)	Скрещивающиеся прямые: не лежат в одной плоскости, не имеют общих точек (не пересекаются)

StudFiles.ru

Стереометрия

Стереометрия (от др.-греч. στερεός, «стереос» — «твёрдый, объёмный, пространственный» и μετρέω, «метрео» — «измеряю») — раздел геометрии, в котором изучаются свойства фигур в пространстве. Основными (простейшими) фигурами в пространстве являются точки, прямые и плоскости. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путём рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Не стоит путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), а в стереометрии — свойства фигур в пространстве (свойства пространственных фигур).

Аксиомы стереометрии

На каждой прямой и в каждой плоскости имеются по крайней мере две точки.
В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;
2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

Многогранник

Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников. Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми и невыпуклыми . Выпуклый многогранник расположен по одну сторону относительно плоскости, проходящей через любую его грань .

Литература

В. В. Прасолов, И. Ф. Шарыгин. Задачи по стереометрии. — М.: Наука, 1989.
И. Ф. Шарыгин. Задачи по геометрии (стереометрия). М.: Наука, 1984. — 160 с. (Библиотечка «Квант», Выпуск 31).

Это заготовка статьи по геометрии. Вы можете помочь проекту, дополнив её.

Разделы математики

Портал «Наука»

Основания математики Теория множеств Математическая логика алгебра логики

Теория чисел (арифметика)

Алгебра Общая алгебра


Элементарная алгебра • Линейная алгебра (Полилинейная алгебра) • Общая алгебра
Коммутативная алгебра • Теория представлений • Дифференциальная алгебра • Гомологическая алгебра • Универсальная алгебра • Теория категорий

Анализ Классический анализ Теория функций Дифференциальные и
интегральные уравнения


Дифференциальное исчисление • Интегральное исчисление
Теория функций вещественного переменного • Теория меры • Комплексный анализ • Кватернионный анализ • Функциональный анализ • Вариационное исчисление • Гармонический анализ
Обыкновенные дифференциальные уравнения • Уравнения в частных производных • Динамические системы и эргодическая теория • Интегральные уравнения
Векторный анализ • Глобальный анализ • Теория катастроф • Нестандартный анализ • Гладкий инфинитезимальный анализ

Геометрия и топология Геометрия Топология

Алгебраическая геометрия • Аналитическая геометрия • Евклидова геометрия • Неевклидова геометрия • Планиметрия • Стереометрия • Тригонометрия

Общая топология • Алгебраическая топология • Дифференциальная геометрия и топология

Дискретная математика

Комбинаторика • Теория графов

Прикладная математика

Математическая физика
Математическая химия
Математическая статистика
Математическое моделирование
Теория алгоритмов
Численные методы
Математическая экономика
Финансовая математика
Теория вероятностей
Исследование операций
Теория игр

Портал «Математика»
Категория «Математика»

ru.wikipedia.org

Какие основные понятия и аксиомы стереометрии

Грустный мир

А1. Через любые три точки не лежащие на одной прямой проходит плоскость и проитом тока одна.
А2 Если 2 точ прямой лежат в плоскости то все точ. этой прямой лежат в плоскости.
А3 Если две плоскости имеют общую точку, то они имеют общию прямую на которой лежать все общие точки.

Следствия:
1. Через прямую и нележащию на ней точку проходит одна плоскость.
2. Через две пересекающиеся прямые проходит плоскость и притом тока одна.

Юрий малихов

Тут нужно уточнить. Любое из этих трех высказываний можно взять исходно за аксиому. Тогда остальные два будут теоремами, доказываемыми на основе взятой аксиомы:
1. Через любые три точки не лежащие на одной прямой проходит плоскость и притом тока одна.
2. Через прямую и нележащию на ней точку проходит одна плоскость.
3. Через две пересекающиеся прямые проходит плоскость и притом тока одна.

Алексей рябчиков

В планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается еще одна основная фигура - плоскость. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
Как и ранее, точки будем обозначать прописными латинскими буквами А, В, С и т. д., а прямые - строчными латинскими буквами а, Ь, с И т. д. или двумя прописными латинскими буквами АВ, CD и т. д. Плоскости будем обозначать греческими буквами а, Р, Y и т. д. На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области .
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. Вся система аксиом стереометрии состоит из ряда аксиом, большая часть которых нам знакома по курсу планиметрии. Мы сформулируем лишь три аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве. Ниже они обозначены А:, А1, А2. A3.
А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Плоскость, проходящую через точки А, В и С, не лежащие на одной прямой, иногда называют плоскостью ABC. Отметим, что если взять не три, а четыре произвольные точки, то через них может не проходить ни одна плоскость. Иначе говоря, четыре точки могут не лежать в одной плоскости. Каждый знаком с таким наглядным подтверждением этого факта: если ножки стула не одинаковые по длине, то стул стоит на трех ножках, т. е. опирается на три "точки", а конец четвертой ножки (четвертая "точка") не лежит в плоскости пола, а висит в воздухе.
А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
В таком случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.
Свойство, выраженное в аксиоме А2, используется для проверки "ровности" чертежной линейки. С этой целью линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный (прямолинейный), то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет."
Из аксиомы А2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются .
А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, что плоскости пересекаются по прямой. Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка классной комнаты.