Определение. Точки максимума и минимума функции называются точками экстремума
Точки экстремума
Определение. Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 +Dx) > f(x2) при любом Dх (Dх может быть и отрицательным).
Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке.
Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.
Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.
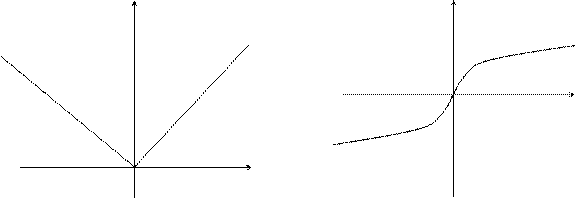
Пример: f(x) = ôxô Пример: f(x) = 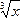
 y y
y y
x
| В точке х = 0 функция имеет минимум, но не имеет производной. | В точке х = 0 функция не имеет ни максимума, ни минимума, ни производной. |
Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.
Теорема. (Достаточные условия существования экстремума)
Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1).
Если при переходе через точку х1 слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.
На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:
1) Найти критические точки функции.
2) Найти значения функции в критических точках.
3) Найти значения функции на концах отрезка.
4) Выбрать среди полученных значений наибольшее и наименьшее.
studopedia.ru
Экстремум
У этого термина существуют и другие значения, см. Экстремум (значения).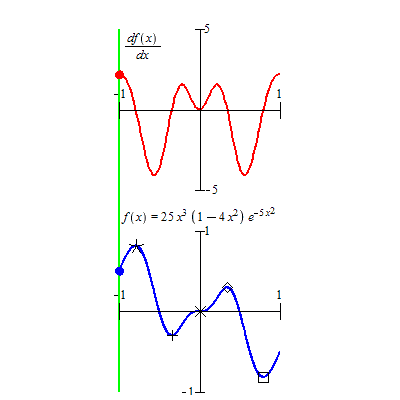 Функция (синяя) и её производная (красная). Глобальный максимум функции обозначен символом 🞯, её глобальный минимум — ☐, локальный максимум — ◇, локальный минимум — +, нуль производной без экстремума — ╳. Видно, что остальные нули производной соответствуют точкам экстремума функции.
Функция (синяя) и её производная (красная). Глобальный максимум функции обозначен символом 🞯, её глобальный минимум — ☐, локальный максимум — ◇, локальный минимум — +, нуль производной без экстремума — ╳. Видно, что остальные нули производной соответствуют точкам экстремума функции.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть дана функция f : M ⊂ R → R , {\displaystyle f:M\subset \mathbb {R} \to \mathbb {R} ,} и x 0 ∈ M 0 {\displaystyle x_{0}\in M^{0}} — внутренняя точка области определения f . {\displaystyle f.} Тогда
- x 0 {\displaystyle x_{0}} называется точкой локального максимума функции f , {\displaystyle f,} если существует проколотая окрестность U ˙ ( x 0 ) {\displaystyle {\dot {U}}(x_{0})} такая, что ∀ x ∈ U ˙ ( x 0 ) f ( x ) ⩽ f ( x 0 ) ; {\displaystyle \forall x\in {\dot {U}}(x_{0})\quad f(x)\leqslant f(x_{0});}
- x 0 {\displaystyle x_{0}} называется точкой локального минимума функции f , {\displaystyle f,} если существует проколотая окрестность U ˙ ( x 0 ) {\displaystyle {\dot {U}}(x_{0})} такая, что ∀ x ∈ U ˙ ( x 0 ) f ( x ) ⩾ f ( x 0 ) . {\displaystyle \forall x\in {\dot {U}}(x_{0})\quad f(x)\geqslant f(x_{0}).}
Если неравенства выше строгие, то x 0 {\displaystyle x_{0}} называется точкой строгого локального максимума или минимума соответственно.
- x 0 {\displaystyle x_{0}} называется точкой абсолютного (глобального) максимума, если ∀ x ∈ M f ( x ) ⩽ f ( x 0 ) ; {\displaystyle \forall x\in M\quad f(x)\leqslant f(x_{0});}
- x 0 {\displaystyle x_{0}} называется точкой абсолютного минимума, если ∀ x ∈ M f ( x ) ⩾ f ( x 0 ) . {\displaystyle \forall x\in M\quad f(x)\geqslant f(x_{0}).}
Значение функции f ( x 0 ) {\displaystyle f(x_{0})} называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
Замечание
Функция f , {\displaystyle f,} определённая на множестве M , {\displaystyle M,} может не иметь на нём ни одного локального или абсолютного экстремума. Например, f ( x ) = x , x ∈ ( − 1 , 1 ) . {\displaystyle f(x)=x,\;x\in (-1,1).}
Необходимые условия существования локальных экстремумов
- Из леммы Ферма вытекает следующее[1]:
Эти условия не являются достаточными, так, функция может иметь нуль производной в точке, но эта точка может не быть точкой экстремума, а являться, скажем, точкой перегиба, как точка (0,0) у функции f ( x ) = x 3 {\displaystyle f(x)=x^{3}} .
Достаточные условия существования локальных экстремумов
- Пусть функция f ∈ C ( x 0 ) {\displaystyle f\in C(x_{0})} непрерывна в x 0 ∈ M 0 , {\displaystyle x_{0}\in M^{0},} и существуют конечные или бесконечные односторонние производные f + ′ ( x 0 ) , f − ′ ( x 0 ) {\displaystyle f'_{+}(x_{0}),f'_{-}(x_{0})} . Тогда при условии
x 0 {\displaystyle x_{0}} является точкой строгого локального максимума. А если
f + ′ ( x 0 ) > 0 , f − ′ ( x 0 ) 0 , {\displaystyle f'_{+}(x_{0})>0,\;f'_{-}(x_{0}) является точкой строгого локального минимума.Заметим, что при этом функция не дифференцируема в точке x 0 {\displaystyle x_{0}} .
- Пусть функция f {\displaystyle f} непрерывна и дважды дифференцируема в точке x 0 {\displaystyle x_{0}} . Тогда при условии
то x 0 {\displaystyle x_{0}} является точкой локального минимума.
- Пусть функция f {\displaystyle f} дифференцируема n {\displaystyle n} раз в точке x 0 {\displaystyle x_{0}} и f ′ ( x 0 ) = f ″ ( x 0 ) = ⋯ = f ( n − 1 ) ( x 0 ) = 0 {\displaystyle f'(x_{0})=f''(x_{0})=\dots =f^{(n-1)}(x_{0})=0} , а f ( n ) ( x 0 ) ≠ 0 {\displaystyle f^{(n)}(x_{0})\neq 0} .
Если n {\displaystyle n} чётно и f ( n ) ( x 0 ) 0 {\displaystyle f^{(n)}(x_{0}) — точка локального максимума. Если n {\displaystyle n} чётно и f ( n ) ( x 0 ) > 0 {\displaystyle f^{(n)}(x_{0})>0} , то x 0 {\displaystyle x_{0}} — точка локального минимума. Если n {\displaystyle n} нечётно, то экстремума нет.
ru.wikipedia.org
Максимум и минимум функций. Необходимые и достаточные условия существования экстремума
Определение. Точка  называется точкой максимума функции у = f (x), если
называется точкой максимума функции у = f (x), если
cуществует такая 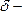 окрестность точки
окрестность точки  , что для всех
, что для всех 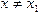 из этой окрестности выполняется неравенство f(x) < f(
из этой окрестности выполняется неравенство f(x) < f(  ).
).
Определение. Точка 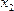 называется точкой минимума функции у = f( x),если
называется точкой минимума функции у = f( x),если
cуществует такая 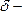 окрестность точки
окрестность точки 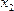 , что для всех
, что для всех 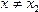 из этой окрестности выполняется неравенство f (x)> f (
из этой окрестности выполняется неравенство f (x)> f ( 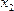 ).
).
Значение функции в точке максимума (минимума) называется максимумом
(минимумом) функции.Максимум (минимумом) функции называется экстремумомфункции.
Теорема 1 (необходимое условие существования экстремума). Если дифференцируемая функция у = f(x) имеет экстремум в точке  , то ее производная в этой точке равна нулю: f¢ (
, то ее производная в этой точке равна нулю: f¢ (  ) = 0.
) = 0.
Обратное утверждение к этой теореме не верно.
Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.
Теорема 2(достаточные условия существования экстремума). Пусть функция f (x) непрерывна в интервале (а, b), который содержит критическую точку  , и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки
, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки  ). Если при переходе через точку
). Если при переходе через точку  слева направо производная функции f¢ (x) меняет знак с плюса на минус, то в точке
слева направо производная функции f¢ (x) меняет знак с плюса на минус, то в точке  функция f (x) имеет максимум, если же производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум, если же производная знака не меняет, то в точке
функция f (x) имеет максимум, если же производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум, если же производная знака не меняет, то в точке  экстремума не существует.
экстремума не существует.
studopedia.ru
1.11. Максимумы и минимумы функции. Нахождение экстремумов функции
Литература: [3], гл. V, § 3
[5], Ч.1, гл. 6, § 6.3
Точка x0 называется точкой максимума (минимума) функции y = f(x), если существует такая окрестность точки x0, что для всех x ≠ x0 из этой окрестности выполняется неравенство f(x) < f(x0) (f(x) > f(x0)).
Точки максимума и минимума функции называются точками экстремума функции, а значения функции в этих точках ─ экстремумами (максимумами и минимумами) функции.
Необходимый признак существования экстремума функции: если непрерывная функция имеет в точке x0 экстремум, то ее производная в этой точке либо равна нулю, либо не существует.
Внутренние точки области определения функции, в которых производная функции равна нулю или не существует, называются критическими.
Первый достаточный признак существования экстремума: если непрерывная функция y = f(x) дифференцируема в некоторой окрестности точки x0 при переходе через эту точку (слева направо) производная ![]() меняет свой знак плюса на минус, тоx0 является точкой максимума, если знак меняется с минуса на плюс, то точка x0 ─ точка минимума. Если знак производной не меняется, то x0 не является точкой экстремума.
меняет свой знак плюса на минус, тоx0 является точкой максимума, если знак меняется с минуса на плюс, то точка x0 ─ точка минимума. Если знак производной не меняется, то x0 не является точкой экстремума.
Пример 1. Найти точки экстремума функции
![]() .
.
Решение. Область определения функции: ![]() .
.
Находим производную функции: ![]() .
.
Находим критические точки: ![]() не существует при
не существует при![]() ,
,![]() при
при![]() . Критические точки
. Критические точки![]() и
и![]() разбивают область определения функции на интервалы (-∞, 0), (0, 1), (1, +∞).
разбивают область определения функции на интервалы (-∞, 0), (0, 1), (1, +∞).
Определяем знаки производной на каждом из интервалов:

В критической точке ![]() производная меняет знак с «+» на «‑». Значит, функция имеет в точке
производная меняет знак с «+» на «‑». Значит, функция имеет в точке![]() максимум. В критической точке
максимум. В критической точке![]() знак производной меняется с «‑» на «+». Следовательно,
знак производной меняется с «‑» на «+». Следовательно,![]() является точкой минимума функции.
является точкой минимума функции.
Второй достаточный признак существования экстремума: если в точке x0 первая производная функции y = f(x) равна нулю, т.е. ![]() , а вторая производная функции существует и отлична от нуля, т.е.
, а вторая производная функции существует и отлична от нуля, т.е.![]() , то точкаx0 является точкой экстремума. При
, то точкаx0 является точкой экстремума. При ![]() в точкеx0 функция имеет максимум, а при
в точкеx0 функция имеет максимум, а при ![]() ─ минимум. В случае, когда
─ минимум. В случае, когда![]() данный признак не дает ответа на вопрос о существовании экстремума.
данный признак не дает ответа на вопрос о существовании экстремума.
Пример 2. Исследовать на экстремум функцию ![]() , пользуясь вторым достаточным признаком существования экстремума.
, пользуясь вторым достаточным признаком существования экстремума.
Решение. Область определения функции: ![]() .
.
Находим первую производную функции: ![]() .
.
![]() при
при ![]() , откуда
, откуда![]() и
и![]() .
.
![]() не существует при
не существует при ![]() .
.
Таким образом, данная функция имеет только одну критическую точку ![]() , поскольку точки
, поскольку точки![]() и
и![]() не входят в область определения функции
не входят в область определения функции![]() .
.
Находим вторую производную функции: ![]() . Вычисляем ее значение в критической точке:
. Вычисляем ее значение в критической точке:![]() . Значит, в точке
. Значит, в точке![]() функция имеет минимум:
функция имеет минимум:![]() .
.
1.12. Нахождение промежутков выпуклости и вогнутости кривой. Точки перегиба
Литература: [3], гл. V, § 9
[5], Ч.1, гл. 6, § 6.4
Кривая называется выпуклой в интервале (а‚b), если все точки кривой лежат не выше любой ее касательной в этом интервале. Кривая называется вогнутой в интервале (а‚b), если ее точки лежат не ниже любой ее касательной в этом интервале (рис. 1.6).
Для нахождения интервалов выпуклости и вогнутости используется вторая производная функции.
Теорема (достаточный признак выпуклости (вогнутости) кривой): если во всех точках некоторого интервала вторая производная функции y = f(x) отрицательна (положительна), то кривая, описываемая уравнением y = f(x), в этом интервале выпуклая (вогнутая).
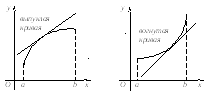
Рис. 1.6
Точка кривой М0(x0, f(x0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.
Теорема (достаточный признак существования точки перегиба): если в точке x0 вторая производная функции y = f(x) равна нулю или не существует и при переходе через эту точку ![]() меняет знак, то точка с абсциссойx = x0 является точкой перегиба графика функции.
меняет знак, то точка с абсциссойx = x0 является точкой перегиба графика функции.
Пример. Найти точки перегиба, интервалы выпуклости и вогнутости кривой ![]() .
.
Решение. Область определения функции: ![]() . Находим первую и вторую производные функции:
. Находим первую и вторую производные функции:
![]() ,
, ![]() .
.
Обе производные существуют при любых значениях x. Приравняв вторую производную к нулю, находим: x0 = 2.
Точка x0 = 2 разбивает область определения функции на интервалы (-∞, 2) и (2, +∞).
Составим таблицу знаков второй производной и поведения функции:
|
x |
(-∞, 2) |
2 |
(2, +∞) |
|
|
− |
0 |
+ |
|
y |
выпуклая |
|
вогнутая |
Знак второй производной меняется в точке x0 = 2. Значит, точка кривой ![]() является точкой перегиба. Слева от этой точки кривая выпуклая (так как
является точкой перегиба. Слева от этой точки кривая выпуклая (так как![]() ), справа ─ вогнутая (так как
), справа ─ вогнутая (так как![]() ).
).
Итак, интервал выпуклости (-∞, 2), вогнутости (2, +∞).
StudFiles.ru
Что такое точка максимума? что такое точка минимума? что такое точка локального экстремума?
Игорь стронин
точка максимума- наибольшее значение функции f(x) на заданом интервале
точка минимума- наименьшее значение функции f(x) на заданом интервале
екстремум- наибольшее или наименьшее значение функции
локальный екстремум - нужно знать с какой области (раздела) математики идет речь, определений есть несколько
Кстати колега выше прав есть и такое определение что производная в точке екстремума =0
Fataleast
точка максимума это типа такая точка, две соседние точки (данной функции) которой расположенны ниже. это как я помню, должна быть самая высокая точка функции.. .
а экстремум, это тоже самое, но точка не обязательно должна быть самой высокой.. . тоесть на локальном отрезке она самая высокая, но в масштабах функции нет :) фух надеюсь доступно обьяснил.
Аs l
Круто.
Это из производных.
помню что в точках максимума минимума первая производная ровна нулю.
точки лок экстремума и есть точки максимума минимума.
Точное определение сейчас не дам (сколько лет прошло) но помню как определить.
Берешь горизонтальную линию и пркладываешь к определяемой точке графика. Если от этой точки график в обе стороны идет вниз - это точка максимума, а если верх - то минимума. Если ни то ни другое - то просто точк графика :))))
Во что помню ышо :)))))
Катя карцева
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум) .
Пусть дана функция f:M \subset \R \to \R, и x_0 \in M^0 — внутренняя точка области определения f. Тогда
* x0 называется точкой локального максимума функции f, если существует проколотая окрестность \dot{U}(x_0) такая, что
\forall x \in \dot{U}(x_0) \quad f(x) \le f(x_0);
* x0 называется точкой локального минимума функции f, если существует проколотая окрестность \dot{U}(x_0) такая, что
\forall x \in \dot{U}(x_0) \quad f(x) \ge f(x_0).
Если неравенства выше строгие, то x0 называется точкой строгого локального максимума или минимума соответственно.
* x0 называется точкой абсолютного (глобального) максимума, если
\forall x\in M\quad f(x) \le f(x_0);
* x0 называется точкой абсолютного минимума, если
\forall x\in M\quad f(x) \ge f(x_0).
Значение функции f(x0) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точка (локального) максимума или минимума, называются точками (локального) экстремума.
Читайте также
![Определение обратной функции Определение обратной функции]() Определение обратной функции
Определение обратной функции![Область определения сложной функции Область определения сложной функции]() Область определения сложной функции
Область определения сложной функции![Понятие функции способы задания функции область определения Понятие функции способы задания функции область определения]() Понятие функции способы задания функции область определения
Понятие функции способы задания функции область определения![Функции нескольких переменных область определения линии уровня Функции нескольких переменных область определения линии уровня]() Функции нескольких переменных область определения линии уровня
Функции нескольких переменных область определения линии уровня![Определение функции нескольких переменных Определение функции нескольких переменных]() Определение функции нескольких переменных
Определение функции нескольких переменных![Определение функции виды функции Определение функции виды функции]() Определение функции виды функции
Определение функции виды функции- Как найти область определения функции
![Как обозначается область определения функции Как обозначается область определения функции]() Как обозначается область определения функции
Как обозначается область определения функции![Электрический ток определение Электрический ток определение]() Электрический ток определение
Электрический ток определение![3 Закон ньютона определение 3 Закон ньютона определение]() 3 Закон ньютона определение
3 Закон ньютона определение- Актив определение
![Акт определение Акт определение]() Акт определение
Акт определение
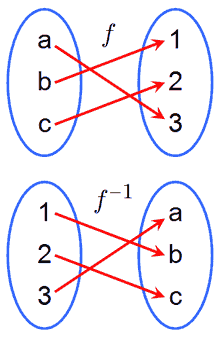 Определение обратной функции
Определение обратной функции Область определения сложной функции
Область определения сложной функции Понятие функции способы задания функции область определения
Понятие функции способы задания функции область определения Функции нескольких переменных область определения линии уровня
Функции нескольких переменных область определения линии уровня Определение функции нескольких переменных
Определение функции нескольких переменных Определение функции виды функции
Определение функции виды функции Как обозначается область определения функции
Как обозначается область определения функции Электрический ток определение
Электрический ток определение 3 Закон ньютона определение
3 Закон ньютона определение Акт определение
Акт определение