Среднее арифметическое это:
Среднее арифметическое У этого термина существуют и другие значения, см. среднее значение.В математике и статистике сре́днее арифмети́ческое - одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их количество.
Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1] и является одной из наиболее распространенных мер центральной тенденции.
Частными случаями среднего арифметического являются генеральное среднее ( генеральной совокупности) и выборочное среднее ( выборки).
Содержание
|
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и в том, что μ является типичной ненаблюдаемой переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.
Примеры
- Для трёх чисел сложим их и поделим на 3:
- Для четырёх чисел сложим их и поделим на 4:
Непрерывная случайная величина
Для непрерывно распределённой величины среднее арифметическое на отрезке определяется через определённый интеграл:
Некоторые проблемы применения среднего
Отсутствие робастности
Основная статья: Робастность в статистикеХотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Основная статья: Окупаемость инвестицийЕсли числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего числа. Если акции в начале стоили $30 и упали на 10 %, они теперь стоят $27. Если акции выросли на 30 %, они теперь стоят $35.1. Арифметическое среднее этого роста 10 %, но поскольку акции выросли за 2 года на $5.1, средний рост в 8,2 % даёт конечный результат $35.1 [$30 (1 — 10 %) (1 + 30 %) = $30 (1 + 8,2 %) (1 + 8,2 %) = $35.1]. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое увеличение [$30 (1 + 10 %) (1 + 10 %) = $36.3].
В общем, сложный процент даёт 90 % * 130 % = 117 % общий рост, а годовой прирост , то есть 8,2 % в год.
Направления
Основная статья: Статистика направленийОсобую осторожность нужно иметь при расчёте циклических данных, таких как фазы или углы. Наивное вычисление среднего арифметического 1° и 359° даёт результат 180°. Это неверно по двум причинам:
- Во-первых, угловые меры определены только до 360° (или 2π, при измерении в радианах). Таким образом, ту же пару можно записать 1° и −1°, или 1° и 719°, но каждая из которых даёт различные средние значения.
- Во-вторых, в этой ситуации, 0° (эквивалентно 360°) геометрически лучшее среднее значение: меньше дисперсия (обе точки на 1° от него, и на 179° от 180°, вычисленного среднего).
В целом применение такого рассмотрения средней величины ведёт к искусственному сдвигу его к середине числового диапазона. Решение этой проблемы заключается в использовании оптимальной формализации (а именно, определение среднего в качестве центральной точки, то есть точки, от которой наименьшая дисперсия), а также переопределение вычитания как модульного расстояния (то есть как расстояние от окружности; в частности, модульное расстояние между 1° и 359° — это 2°, а не 358°).
Примечания
- ↑ Cantrell, David W., "Pythagorean Means" from MathWorld
См. также
- Взвешенное среднее
- Винсоризованное среднее
- Гармоническое среднее
- Геометрическое среднее
- Медиана
- Мода
- Среднее Колмогорова
- Усеченное среднее
- Неравенство между средним арифметическим и средним геометрическим
- Неравенство Швейцера
Ссылки
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика
- Прикладная математика
статистика Статистический
вывод и
проверка
гипотез Корреляция
|
||||||||||||
|
||||||||||||
| Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания | ||||||||||||
| Линейные модели | Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ | |||||||||||
| Регрессия | Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия |
- Средние величины
Wikimedia Foundation. 2010.
dic.academic.ru
Среднее значение
Сре́днее значе́ние — числовая характеристика множества чисел или функций (в математике); — некоторое число, заключённое между наименьшим и наибольшим из их значений.
Основные сведения
Исходным пунктом становления теории средних величин явилось исследование пропорций школой Пифагора. При этом не проводилось строгого различия между понятиями средней величины и пропорции. Значительный толчок развитию теории пропорций с арифметической точки зрения был дан греческими математиками — Никомахом Герасским (конец I — начало II в. н. э.) и Паппом Александрийским (III в. н. э.). Первым этапом развития понятия средней является этап, когда средняя стала считаться центральным членом непрерывной пропорции. Но понятие средней как центрального значения прогрессии не даёт возможности вывести понятие средней по отношению к последовательности n членов, независимо от того, в каком порядке они следуют друг за другом. Для этой цели необходимо прибегнуть к формальному обобщению средних. Следующий этап — переход от непрерывных пропорций к прогрессиям — арифметической, геометрической и гармонической (англ.)[1].
В истории статистики впервые широкое употребление средних величин связано с именем английского учёного У. Петти. У. Петти один из первых пытался придать средней величине статистический смысл, связав её с экономическими категориями. Но описания понятия средней величины, его выделения, Петти не произвёл. Родоначальником теории средних величин принято считать А. Кетле. Он одним из первых начал последовательно разрабатывать теорию средних величин, пытаясь подвести под неё математическую базу. А. Кетле выделял два вида средних величин — собственно средние и средние арифметические. Собственно средние представляют вещь, число, действительно существующие. Собственно средние или средние статистические должны выводиться из явлений однокачественных, одинаковых по своему внутреннему значению. Средние арифметические — числа, дающие возможно близкое представление о многих числах, различных, хотя и однородных[2].
Каждый из видов средней может выступать либо в форме простой, либо в форме взвешенной средней. Правильность выбора формы средней вытекает из материальной природы объекта исследования. Формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются. Когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторений индивидуальных значений признака присутствует в расчётных формулах степенных средних. В этом случае они называются формулами взвешенных средних.[3]
Иерархия средних значений в математике
- среднее значение функции — понятие, определяемое многими способами.
- Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
- среднее степенное — частный случай средних Колмогорова при ϕ ( x ) = x α {\displaystyle \phi (x)=x^{\alpha }} . Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
- среднее арифметическое ( α = 1 {\displaystyle \alpha =1} );
- среднее квадратическое ( α = 2 {\displaystyle \alpha =2} );
- среднее гармоническое ( α = − 1 {\displaystyle \alpha =-1} );
- по непрерывности при α → 0 {\displaystyle \alpha \to 0} доопределяется среднее геометрическое, которое также является Колмогоровским средним при ϕ ( x ) = log x {\displaystyle \phi (x)=\log x}
- среднее степенное — частный случай средних Колмогорова при ϕ ( x ) = x α {\displaystyle \phi (x)=x^{\alpha }} . Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
- Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
- Среднее взвешенное — обобщение средней величины на случай произвольной линейной комбинации:
- Среднее арифметическое взвешенное.
- Среднее геометрическое взвешенное.
- Среднее гармоническое взвешенное.
- среднее хронологическое — обобщает значения признака для одной и той же единицы или совокупности в целом, изменяющихся во времени.
- среднее логарифмическое, определяемое по формуле a ¯ = a 1 − a 2 ln ( a 1 / a 2 ) {\textstyle {\bar {a}}={\frac {a_{1}-a_{2}}{\ln(a_{1}/a_{2})}}} , используется в теплотехнике
- среднее логарифмическое, определяемое в электроизоляции соответствии с ГОСТ 27905.4-88 определяется как l o g a ¯ = log a 1 + l o g a 2 + . . . + . . . l o g a n a 1 + a 2 + . . . + a n {\textstyle log{\bar {a}}={\frac {\log a_{1}+loga_{2}+...+...loga_{n}}{a_{1}+a_{2}+...+a_{n}}}} (логарифм по любому основанию)[4]
В теории вероятностей и статистике
Основная статья: Показатели центра распределения- непараметрические средние — мода, медиана.
- среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.
ru.wikipedia.org
1.3. Буквенные обозначения величин
|
I |
— |
ток, действующее значение; |
|
i |
— |
ток, мгновенное значение; |
|
|
— |
ток комплексный, действующее значение; |
|
Im |
— |
ток, амплитудное значение; |
|
Iном |
— |
номинальный ток; |
|
iуд |
— |
ударный ток КЗ; |
|
iдин |
— |
ток электродинамической стойкости; |
|
Iвкл,iвкл |
— |
ток включения, действующее и мгновенное значения; |
|
Iскв,iскв |
— |
сквозной ток, действующее и мгновенное значения; |
|
Iпр.скв,iпр.скв |
— |
предельный сквозной ток, действующее и мгновенное значения; |
|
Iоткл,iоткл |
— |
отключаемый ток, действующее и мгновенное значения; |
|
Iоткл.ном,iоткл.ном |
— |
номинальный ток отключения электрического аппарата; |
|
It, it |
— |
ток в момент t; |
|
I, i |
— |
ток в момент , |
|
Iтер |
— |
ток термической стойкости; |
|
I |
— |
ток установившегося режима; |
|
Iк |
— |
ток КЗ, общее обозначение |
|
Iп;iп |
— |
периодическая составляющая тока КЗ; |
|
Iа;iа |
— |
апериодическая составляющая тока КЗ (Iа =iа); |
|
Iп0 |
— |
начальное действующее значение периодической составляющей тока КЗ (t= 0); |
|
ia0 |
— |
начальное значение апериодической составляющей тока КЗ (t= 0); |
|
Iп, iа |
— |
периодическая и апериодическая составляющие тока КЗ в момент t =; |
|
IA, IВ, IС |
— |
токи соответственно фаз А, В, С; |
|
IN |
— |
ток в нейтральном проводе; |
|
I1, I2, I0 |
— |
ток соответственно прямой, обратной и нулевой последовательностей; |
|
Iож,iож |
— |
ток, ожидаемый в цепи с токоограничивающим аппаратом; |
|
I |
— |
ток суммарный; |
|
Iпрод.доп |
— |
ток продолжительного режима, допустимый; |
|
Iнорм.расч |
— |
ток нормального режима, расчетный; |
|
Iпрод.расч |
— |
ток продолжительного режима, расчетный; |
|
Id, Iq |
— |
токи соответственно по осям d иq; |
|
I' |
— |
переходный ток; |
|
I" |
— |
сверхпереходный ток; |
|
iпл |
— |
ток плавления вставки предохранителя; |
|
U,и |
— |
напряжение, действующее и мгновенное значения; |
|
Uраб.нб |
— |
наибольшее рабочее напряжение; |
|
Uном |
— |
номинальное напряжение; |
|
U1, U2, U0 |
— |
напряжения соответственно прямой, обратной и нулевой последовательностей; |
|
U |
— |
потеря напряжения; |
|
|
— |
угол сдвига фаз между напряжением и током; |
|
cos |
— |
коэффициент мощности; |
|
E,e |
— |
электродвижущая сила, действующее и мгновенное значения; |
|
Р |
— |
мощность активная; |
|
Q |
— |
мощность реактивная; |
|
S |
— |
мощность полная, модуль; |
|
|
— |
мощность полная, комплексная; |
|
f |
— |
частота колебаний электрической величины; |
|
|
— |
частота колебаний электрической величины, угловая; |
|
R, r |
— |
сопротивление активное; |
|
Х, х |
— |
сопротивление реактивное; |
|
Z |
— |
сопротивление полное, модуль; |
|
|
— |
сопротивление полное, комплексное; |
|
XL |
— |
сопротивление реактивное, индуктивное; |
|
XC |
— |
сопротивление реактивное, емкостное; |
|
Zв |
— |
сопротивление волновое; |
|
ив |
— |
восстанавливающееся напряжение на контактах коммутационного аппарата; |
|
в |
— |
скорость восстановления напряжения; |
|
Uвз,uвз |
— |
возвращающееся напряжение на контактах коммутационного аппарата; |
|
Z1, Z2, Z0 |
— |
сопротивления соответственно прямой, обратной и нулевой последовательностей; |
|
Y |
— |
проводимость электрическая, модуль; |
|
|
— |
проводимость электрическая, комплексная; |
|
g |
— |
проводимость активная; |
|
b |
— |
проводимость реактивная; |
|
L |
— |
индуктивность собственная; |
|
M |
— |
индуктивность взаимная; |
|
Kсв |
— |
коэффициент связи; |
|
|
— |
коэффициент рассеяния; |
|
|
— |
удельное сопротивление; |
|
|
— |
удельная проводимость; |
|
|
— |
температурный коэффициент сопротивления; |
|
|
— |
температурный коэффициент теплоемкости; |
|
Wэ |
— |
энергия электрическая; |
|
Wэм |
— |
энергия электромагнитная; |
|
Н |
— |
напряженность магнитного поля, модуль; |
|
|
— |
напряженность магнитного поля, вектор; |
|
Е |
— |
напряженность электрического поля, модуль; |
|
|
— |
напряженность электрического поля, вектор; |
|
|
— |
проницаемость диэлектрическая абсолютная; |
|
r |
— |
проницаемость диэлектрическая относительная; |
|
0 |
— |
постоянная электрическая; |
|
|
— |
проницаемость магнитная абсолютная; |
|
r |
— |
проницаемость магнитная относительная; |
|
0 |
— |
постоянная магнитная; |
|
|
— |
температура в шкале Цельсия; |
|
T |
— |
температура в шкале Кельвина; |
|
|
— |
превышение температуры; |
|
T |
— |
постоянная времени электрической цепи; |
|
T |
— |
период колебаний электрической величины; |
|
Ta |
— |
постоянная времени затухания апериодической составляющей тока КЗ; |
|
Kуд |
— |
ударный коэффициент; |
|
норм |
— |
нормированное процентное содержание апериодической составляющей в отключаемом токе; |
|
n |
— |
коэффициент трансформации; |
|
n |
— |
отношение числа витков; |
|
N |
— |
число витков обмотки; |
|
С |
— |
емкость; |
|
с |
— |
удельная теплоемкость; |
|
|
— |
плотность материала; |
|
s |
— |
скольжение; |
|
sкр |
— |
скольжение критическое; |
|
S |
— |
сечение проводника; |
|
М |
— |
момент вращающихся масс; |
|
Tj |
— |
постоянная инерции (механическая постоянная); |
|
F |
— |
поверхность; |
|
|
— |
сила, вектор; |
|
F |
— |
сила, модуль; |
|
q |
— |
удельная теплоотдача; |
|
Ф |
— |
тепловой поток; |
|
Е |
— |
модуль упругости; |
|
J |
— |
момент инерции; |
|
W |
— |
момент сопротивления поперечного сечения проводника; |
|
т |
— |
масса; |
|
|
— |
напряжение в материале; |
|
пч |
— |
предел прочности; |
|
пц |
— |
предел пропорциональности; |
|
т |
— |
предел текучести; |
|
Kф |
— |
коэффициент формы; |
|
Kд |
— |
коэффициент добавочных потерь; |
|
Kд |
— |
коэффициент динамической нагрузки; |
|
Kп |
— |
коэффициент поверхностного эффекта; |
|
Kпг |
— |
коэффициент перегрузки; |
|
Вк |
— |
интеграл Джоуля при КЗ; |
|
Втер |
— |
нормированный интеграл Джоуля электрического аппарата для условий КЗ; |
|
tтер |
— |
время термической стойкости электрического аппарата; |
|
tоткл |
— |
время отключения КЗ, расчетная продолжительность КЗ; |
|
tс.в.откл |
— |
собственное время отключения выключателя; |
|
tв.откл |
— |
полное время отключения выключателя; |
|
tр.зmin |
— |
минимальное расчетное время срабатывания релейной защиты; |
|
|
— |
момент начала расхождения дугогасительных контактов коммутационного аппарата; |
|
|
— |
коэффициент динамической нагрузки; |
|
с |
— |
коэффициент расчетного эквивалентного напряжения сети; |
|
а |
— |
расстояние между фазами; |
|
|
— |
логарифмический декремент затухания; |
|
tбт |
— |
бестоковая пауза в цикле АПВ. |
StudFiles.ru
Что такое среднее арифметическое? Как найти среднее арифметическое?
Формула среднего арифметического чисел?
Алекс-89
Среднее арифметическое нескольких чисел — это сумма этих чисел, делённая на их количество.
x ср = S/n
где:
x ср — среднее арифметическое
S — сумма чисел
n — количество чисел.
Например, нам нужно найти среднее арифметическое чисел 3, 4, 5 и 6.
Для этого нам нужно их сложить и полученную сумму разделить на 4:
(3 + 4 + 5 + 6) : 4 = 18 : 4 = 4,5.
Алсу - ш
Мне, как математику, интересны вопросы по данному предмету.
Начну с истории вопроса. Над средними величинами задумывались с древних времмен. Среднее арифметическое, среднее геометоическое, среднее гармоническое. Эти понятия предложены в древней Греции пифагорийцами.
А теперь интересующий нас вопрос. Что же понимается под средним арифметичским нескольких чисел:

Итак, для нахождения среднего арифметического чисел нужно прибавить все числа и разделить полученную сумму на количество слагаемых.
Имеет место формула:
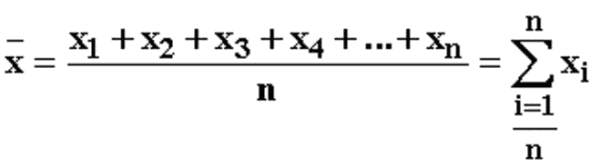
Пример. Найти среднее арифметическое чисел: 100, 175, 325.
Решение.
Воспользуемся формулой нахождения среднего арифметического трех чисел (то есть вместо n будет 3; нужно сложить все 3 числа и разделить полученную сумму на их количество, т.е. на 3). Имеем: х=(100+175+325)/3=600/3=200.
Ответ: 200.
Lady v
Арифметика считается самым элементарным разделом математики и изучает простые действия с числами. Поэтому и среднее арифметическое также находится очень просто. Начнем с определения. Среднее арифметическое - это величина, которая показывает какое число наиболее близко к истине при нескольких последовательных однотипных действиях. Например при беге на сто метров человек каждый раз показывает разное время, но средняя величина будет в пределах например 12 секунд. Нахождение среднего арифметического таким образом сводится в последовательному суммированию всех чисел определенного ряда (результатов забегов) и деление этой суммы на количество этих забегов (попыток, чисел). В виде формулы это выглядит так:
Sариф = (Х1+Х2+..+Хn)/n
Mb78
Среднее арифметическое - это среднее число между несколькими числами.
Например между числами 2 и 4 среднее число 3.
Формула нахождения среднего арифметического такая:
Нужно сложить все числа и разделить на количество этих чисел:
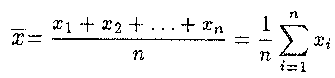
Например у нас 3 числа: 2, 5 и 8.
Находим среднее арифметическое:
X=(2+5+8)/3=15/3=5
Область применения среднего арифметического достаточно широка.
Например можно зная координаты двух точек отрезка найти координаты середины этого отрезка.
Например координаты отрезка: (X1,Y1,Z1)-(X2,Y2,Z2).
Обозначим середину этого отрезка координатами X3,Y3,Z3.
Отдельно находим середину для каждой координаты:
X3=(X1+X2)/2;
Y3=(Y1+Y2)/2;
Z3=(Z1+Z2)/2;
Красивая поляна
Средне арифметическое число, это числа сложенные вместе и деленные на их количество, полученный ответ и есть средне арифметическое число.
Например: Катя положила в копилку 50 рублей, Максим 100 рублей, а Саша положил в копилку 150 рублей. 50 + 100 + 150 = 300 рублей в копилке, теперь делим эту сумму на три (три человека положили деньги). Итак 300 : 3 = 100 рублей. Эти 100 рублей и будет средне арифметически, каждый из них положил в копилку.
Есть такой простой пример: один человек ест мясо, другой человек ест капусту, а средне арифметически они оба едят голубцы.
Таким же образом рассчитывают среднюю зарплату...
Simpl
Среднеарифметическое-это среднее значение из заданных...
Т.е. по простому имеем количество палочек разной длины и хотим узнать их среднее значение..
Логично, что для этого мы их сводим вместе, получая длинную палку, а потом делим её на требуемое число частей..
Вот и выходит среднеарифметическое..
Вот так и выводится формула:Sa=(S(1)+..S(n))/n..
Птичка2014
Среднее арифметическое - это сумма всех значений и деленное на их количество.
Например числа 2, 3 , 5, 6 . Нужно их сложить 2+ 3+ 5 + 6 = 16
16 делим на 4 и получаем ответ 4 .
4 и есть среднее арифметическое этих чисел.
Azamatik
Средним арифметическим называют сумму чисел, разделенное на количество этих самых чисел. А найти среднее арифметическое очень просто.
Как следует из определения мы должны взять числа, сложить их и разделить на их количество.
Приведем пример: дается числа 1, 3, 5, 7 и нам надо найти среднее арифметическое этих чисел.
- сначала складываем эти числа (1+3+5+7) и получаем 16
- полученный результат нам надо разделить на 4 (кол - во): 16/4 и получаем результат 4.
Итак, среднее арифметическое чисел 1, 3, 5 и 7 - это 4.
Tana76
Среднее арифметическое - среднее значение среди заданных показателей.
Оно находится путем деления суммы всех показателей на их количество.
Например, у меня есть 5 яблок весом 200, 250, 180, 220 и 230 грамм.
Средний вес 1 яблока находим так:
- ищем общий вес всех яблок (сумму всех показателей) - он равен 1080 граммов,
- делим общий вес на количество яблок 1080:5 = 216 граммов. Это и есть среднее арифметическое.
Это наиболее часто применяемый в статистике показатель.
Зеленый чебуречек
Это мы знаем со школьной скамьи. У кого был хороший учитель по математике, то запомнить это нехитрое действие можно было с первого раза.
При нахождении среднего арифметического необходимо сложить все имеющиеся числа и разделить на их количество.
Например, я купила в магазине 1 кг яблок, 2 кг бананов, 3 кг апельсинов и 1 кг киви. Сколько килограммов в среднем я купила фруктов.
1+2+3+1=7.
7/4= 1,8 килограммов. Это и будет среднеарифметическим значением.
Бьемон эпу
Помню как итоговую контрольную по математике сдавал
Так там нужно было среднее арифметическое найти.
Хорошо что добрые люди подсказали что делать, иначе беда.
Например у нас 4 числа.
Складываем числа и делим на их количество (в данном случае 4)
Например цифры 2,6,1,1. Складываем 2+6+1+1 и делим на 4 = 2.5
Как видите ничего сложного. Так что среднее арифметическая - это среднее значение всех чисел.
bolshoyvopros.ru
Читайте также
![Обозначение среднего значения Обозначение среднего значения]() Обозначение среднего значения
Обозначение среднего значения![Среднее квадратическое значение применяется для расчета Среднее квадратическое значение применяется для расчета]() Среднее квадратическое значение применяется для расчета
Среднее квадратическое значение применяется для расчета![Как высчитать среднее значение Как высчитать среднее значение]() Как высчитать среднее значение
Как высчитать среднее значение![Среднее значение функции на отрезке Среднее значение функции на отрезке]() Среднее значение функции на отрезке
Среднее значение функции на отрезке![Среднее значение формула Среднее значение формула]() Среднее значение формула
Среднее значение формула![Сущность и значение средних величин Сущность и значение средних величин]() Сущность и значение средних величин
Сущность и значение средних величин![Среднее и действующее значение синусоидального тока Среднее и действующее значение синусоидального тока]() Среднее и действующее значение синусоидального тока
Среднее и действующее значение синусоидального тока![Среднее арифметическое значение формула Среднее арифметическое значение формула]() Среднее арифметическое значение формула
Среднее арифметическое значение формула![Среднее арифметическое значение Среднее арифметическое значение]() Среднее арифметическое значение
Среднее арифметическое значение![Расчет среднего значения Расчет среднего значения]() Расчет среднего значения
Расчет среднего значения![Символ среднего значения Символ среднего значения]() Символ среднего значения
Символ среднего значения![Среднее значение Среднее значение]() Среднее значение
Среднее значение



 Среднее квадратическое значение применяется для расчета
Среднее квадратическое значение применяется для расчета Как высчитать среднее значение
Как высчитать среднее значение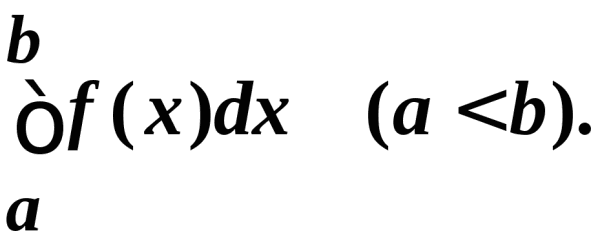 Среднее значение функции на отрезке
Среднее значение функции на отрезке Среднее значение формула
Среднее значение формула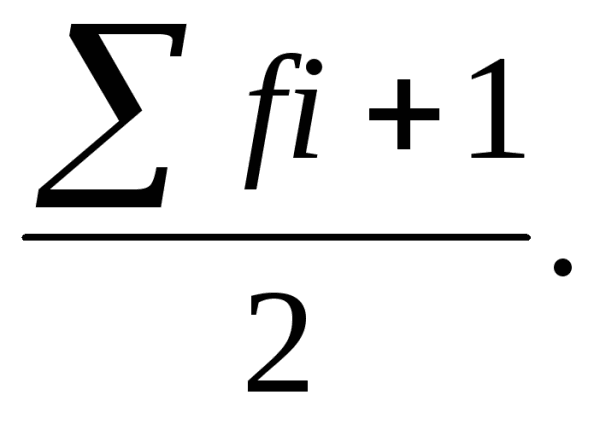 Сущность и значение средних величин
Сущность и значение средних величин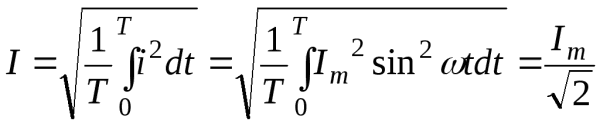 Среднее и действующее значение синусоидального тока
Среднее и действующее значение синусоидального тока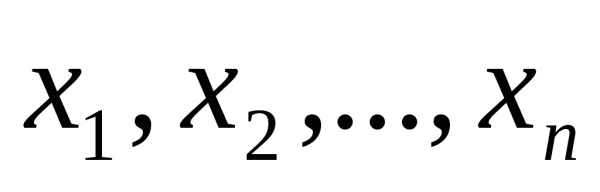 Среднее арифметическое значение формула
Среднее арифметическое значение формула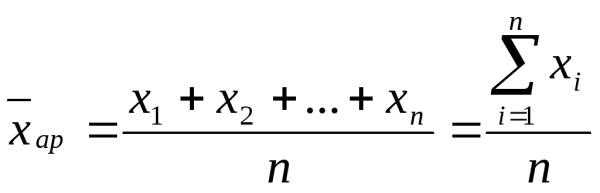 Среднее арифметическое значение
Среднее арифметическое значение Расчет среднего значения
Расчет среднего значения Символ среднего значения
Символ среднего значения Среднее значение
Среднее значение