Коэффициент корреляции
 Коэффициент корреляции – это величина, которая может варьировать в пределах от +1 до –1. В случае полной положительной корреляции этот коэффициент равен плюс 1 (говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной), а при полной отрицательной – минус 1 (свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются).
Коэффициент корреляции – это величина, которая может варьировать в пределах от +1 до –1. В случае полной положительной корреляции этот коэффициент равен плюс 1 (говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной), а при полной отрицательной – минус 1 (свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются).
 Пр1.:
Пр1.:
График зависимости застенчивости и дипресивности. Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны.
 Пр2.: График для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)
Пр2.: График для Застенчивости и Общительности. Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…)
 В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников.
Используется две системы классификации корреляционных связей по их силе: общая и частная.
Общая классификация корреляционных связей:1) сильная, или тесная при коэффициенте корреляции r>0,70;2) средняя при 0,500,70, а не просто корреляция высокого уровня значимости.В следующей таблице написаны названия коэффициентов корреляции для различных типов шкал.
| Дихотомическая шкала (1/0) | Ранговая (порядковая) шкала | Интервальная и абсолютная шкала | |
| Дихотомическая шкала (1/0) | Коэфициент ассоциации Пирсона, коэффициент четырехклеточной сопряженности Пирсона. | Рангово-бисериальная корреляция. | Бисериальная корреляция |
| Ранговая (порядковая) шкала | Рангово-бисериальная корреляция. | Ранговый коэффициент корреляции Спирмена или Кендалла. | Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент |
| Интервальная и абсолютная шкала | Бисериальная корреляция | Значения интервальной шкалы переводятся в ранги и используется ранговый коэффициент | Коэффициент корреляции Пирсона (коэффициент линейной корреляции) |
При r=0линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общими средними, а линии регрессии параллельны осям координат.
Равенство r=0говорит лишь об отсутствии линейной корреляционной зависимости (некоррелированности переменных), но не вообще об отсутствии корреляционной, а тем более, статистической зависимости.
Иногда вывод об отсутствии корреляции важнее наличия сильной корреляции. Нулевая корреляция двух переменных может свидетельствовать о том, что никакого влияния одной переменной на другую не существует, при условии, что мы доверяем результатам измерений.
В SPSS: 11.3.2 Коэффициенты корреляции
До сих пор мы выясняли лишь сам факт существования статистической зависимости между двумя признаками. Далее мы попробуем выяснить, какие заключения можно сделать о силе или слабости этой зависимости, а также о ее виде и направленности. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения — большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.
В качестве коэффициента корреляции между переменными, принадлежащими порядковой шкале применяется коэффициент Спирмена, а для переменных, принадлежащих к интервальной шкале — коэффициент корреляции Пирсона (момент произведений). При этом следует учесть, что каждую дихотомическую переменную, то есть переменную, принадлежащую к номинальной шкале и имеющую две категории, можно рассматривать как порядковую.
Для начала мы проверим существует ли корреляция между переменными sex и psyche из файла studium.sav. При этом мы учтем, что дихотомическую переменную sex можно считать порядковой. Выполните следующие действия:
· Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
· Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
· Щелкните на кнопке Statistics... (Статистика). В диалоге Crosstabs: Statistics установите флажок Correlations (Корреляции). Подтвердите выбор кнопкой Continue.
· В диалоге Crosstabs откажитесь от вывода таблиц, установив флажок Supress tables (Подавлять таблицы). Щелкните на кнопке ОК.
Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:
studopedia.ru
/ Парная корреляция
Парная корреляция
Часто при проведении маркетингового исследования нас интересует связь между двумя метрическими переменными, как, например, в следующих ситуациях.
Насколько сильно связан объем продаж с затратами на рекламу?
Существует ли связь между долей рынка фирмы и численностью ее торгового персонала?
Связано ли восприятие качества товаров потребителями с их восприятием цены?
В таких ситуациях наиболее широко используемой статистикой является коэффициент парной Корреляции, (commercial units moment Correlation r), который характеризует степень тесноты связи между двумя метрическими (измеряемыми с помощью интервальной или относительной шкал) переменными, скажем, Х и Y. Этот коэффициент используют, чтобы определить, существует ли между переменными линейная зависимость. Он показывает степень, в которой вариация одной переменной X связана с вариацией другой переменной Y, т.е. меру зависимости между переменными Х и Y.
Коэффициент парной Корреляции, г (commercial units moment Correlation r)
Статистический показатель, характеризующий степень тесноты связи между двумя метрическими переменными.
Поскольку этот коэффициент первоначально предложил Карл Пирсон, его также называют коэффициентом Корреляции Пирсона. Кроме того, он известен как простой коэффициент Корреляции, линейный коэффициент Корреляции или просто коэффициент Корреляции.
В этих уравнениях X и Y обозначают выборочные средние, а — соответствующие стандартные отклонения; COV представляет собой ковариацию (covari-апсе) между Х и Y, т.е. меру зависимости Xи Y.
Ковариация может быть как положительной, так и отрицательной. Деление на SxS приводит к нормированному виду, так что коэффициент Корреляции г находится в пределах от -1 до +1. Обратите внимание, что коэффициент Корреляции никак не связан с единицами измерения, в которых выражены переменные.
Предположим, что исследователь хочет выяснить, зависит ли отношение респондента к местожительству от длительности его проживания в этом городе. Отношение выражают в 11- балльной шкале (1 — не нравится город, 11 — очень нравится город), а продолжительность проживания измеряют количеством лет, которые респондент прожил в этом городе.
В этом примере г = 0,9361, что близко к 1. Это означает, что отношение респондента к своему городу сильно зависит от времени проживания в нем. Более того, положительный знак г указывает на прямую связь (прямо пропорциональную): чем дольше респондент проживает в городе, тем больше он ему нравится, и наоборот.
Поскольку коэффициент Корреляции показывает меру, в которой вариация значений одной переменной зависит от вариации другой, можно выразить через разложение полной вариации.
Следовательно, г2 показывает, какая доля вариации одной переменной обусловлена вариацией другой. И г, и г2 являются симметричными показателями связи между переменными. Иначе говоря, корреляция между Х и Y та же, что и корреляция между Y и X. Корреляция не зависит от того, какая из переменных взята в качестве зависимой, а какая — в качестве независимой. Коэффициент Корреляции является мерой линейной зависимости, и он не предназначен для измерения силы связи в случае нелинейной зависимости. Таким образом, г = 0 просто означает отсутствие линейной зависимости между Х и Y. Это не означает, что Х и Y не взаимосвязаны. Между ними может существовать нелинейная зависимость, которую нельзя определить с помощью коэффициента Корреляции г.
Если коэффициент Корреляции вычисляют не для выборки, а для всей генеральной совокупности, то он обозначается греческой буквой р (ро). Коэффициент г — это оценка р. Обратите внимание, что расчет г предполагает, что X и Y- метрические переменные, кривые распределения которых имеют одинаковую форму. Если эти допущения не удовлетворяются, то значение г уменьшается и р получается недооцененным. В маркетинговых исследованиях данные, полученные с использованием относительной шкалы при небольшом количестве категорий, могут не быть строго интервальными.



Статистику, лежащую в основе критерия для проверки гипотезы, вычисляют по формуле которая имеет распределение с (п — 2) степенями свободы. Для коэффициента Корреляции, вычисленного на основе данных, а число степеней свободы- 12- 2 = 10. Следовательно, нулевую гипотезу об отсутствии связи между переменными Х и Y отклоняют. Это, наряду с положительным знаком коэффициента Корреляции, показывает, что отношение респондента к своему городу прямо пропорционально зависит от продолжительности проживания в нем. Более того, высокое значение г свидетельствует о том, что эта связь сильная.
При выполнении многомерного анализа данных часто полезно изучить простую Корреляцию между каждой парой переменных. Эти результаты представляют в форме корреляционной матрицы, которая показывает коэффициент Корреляции между каждой парой данных. Обычно рассматривают только самую нижнюю треугольную часть матрицы. Все элементы по диагонали равны 1,00, так как переменная коррелирует сама с собой. Верхняя треугольная часть матрицы — зеркальное отражение нижней треугольной части матрицы, поскольку г — симметричный показатель связи между переменными.
Хотя матрица простых коэффициентов Корреляций позволяет уяснить суть по парных связей, иногда исследователю хочется изучить связи между двумя переменными при условии управления одной или несколькими переменными. В последнем случае следует оценивать частную Корреляцию. В последние годы понятие и применение in vitro — in vivo Корреляции (IVIVC) для фармацевтических дозированных лекарственных форм стали одними из центральных предметов рассмотрения фармацевтической промышленностью, ВУЗами и регулирующими организациями. Поскольку разработка и оптимизация технологических составов (прописей) — неотъемлемая часть производства и анализа рынка любого терапевтического средства, они являются наиболее трудоемкими и дорогостоящими. В процессе оптимизации могут потребоваться изменения технологической части, производства, оборудования или масштабов производства. Если таковые типы изменений применены к технологической прописи, то исследования на здоровых добровольцах необходимо повторять для подтверждения того, что новая пропись биоэквивалентна старой. Безусловно, выполнение этих требований не только тормозит анализ конъюнктуры рынка новой технологической прописи, но также и увеличивает цена ее оптимизации. Таким образом, на сегодняшний день для производителей предпочтительнее и экономически выгоднее разрабатывать тесты in vitro, которые будут адекватно отражать исследования биодоступности.
Регуляторные руководства для дозированных форм как немедленного, так и модифицированного высвобождения, были разработаны FDA. Актуальность их создания заключалась, во-первых, в уменьшении необходимости проведения исследований биодоступности, а вовторых, они требовались для замены устаревших методов разработки и оптимизации технологических прописей.
Как указывалось выше, разработка IVIVC главным образом нацелена на то, чтобы частично или полностью заменить испытания на здоровых добровольцах в течение всего периода создания препарата. В дополнение к этому, IVIVC также можно использовать для изучения IVIVC спецификаций и для валидации методик растворения. Такое применение данного метода заключено в его определении. Данный метод также может стать серьезным подспорьем в процессе контроля качества в случае масштабирования производства (например, для улучшения состава технологической прописи или внесения изменений в производственный процесс) и / или внесения пострегистрационных изменений. При этом следует учитывать, что данные in vitro будут гарантироваться тем, что каждая политическая партияодного и того же препарата будет действовать идентично in vivo.
С быстрым увеличением препаратов с модифицированным высвобождением, существенно повысилась и значимость более глубокого изучения IVIVC. Хотя акцент дискуссии в этом обзоре будет, прежде всего, сосредоточен на технологических формах с модифицированным высвобождением, для которых считается, что IVIVC лучше прогнозируется, также будут рассмотрены некоторые аспекты ее применения и для технологических форм с немедленным высвобождением.
Коэффициент парной корреляции
Коэффициент парной корреляции вычисляется по формуле:
 или
или 
Алгоритм расчета коэффициента парной корреляции:
1) записывают исходные данные в два вариационных ряда – x и y;
2) вычисляют среднюю арифметическую ряда x и y;
3) определяют разность между членом ряда и средними величинами;
4) перемножают разности ряда x и y между собой;
5) находят сумму перемножаемых разностей (с учетом арифметического знака);
6) возводят в квадрат каждую разность (отклонение) ряда х и у;
7) определяют сумму квадратов отклонений (разностей) для ряда х и у отдельно;
8) подставляют полученные данные в исходную формулу и вычисляют коэффициент парной корреляции.
Пример. Определить корреляционную связь между строками введения противодифтерийной сыворотки и летальностью от этого заболевания.
|
День введения сыворотки (х) |
Летальность (у) |
dx |
dy |
dx2 |
dy2 |
dx*dx |
|
1-й |
2,0 |
-2 |
-5 |
4 |
25 |
10 |
|
2-й |
3,0 |
-1 |
-4 |
1 |
16 |
4 |
|
3-й |
7,0 |
0 |
0 |
0 |
0 |
0 |
|
4-й |
9,0 |
+1 |
+2 |
1 |
4 |
2 |
|
5-й |
14,0 |
+2 |
+7 |
4 |
49 |
14 |
|
xx = 3 |
xy = 7.0 |
Sdx=0 |
Sdy=0 |
Sdx2=10 |
Sdy2=94 |
Sdx*dy =30 |
![]()
Коэффициент корреляции равен +0,98. Связь положительная, сильная. Следовательно, между сроками введения сыворотки и летальностью от дифтерии имеется очень тесная зависимость. Число больных в этом примере равно 900.
Можно определить достоверность коэффициента корреляции, вычислив его среднюю ошибку для большого числа наблюдений (n>50) по формуле:
![]() , или при меньшем числе наблюдений:
, или при меньшем числе наблюдений: ![]()
С достаточно большой надежностью можно утверждать, что зависимость неслучайна, если численное значение rxy превышает свою среднюю ошибку не менее чем в 3 раза.
![]()
Т.е. связь между признаками считается статистически значимой, если коэффициент корреляции превышает свою ошибку в 3 и более раз
В том случае, когда отношение коэффициента корреляции к его средней ошибки меньше 3, существование связи между изучаемыми явлениями нельзя признать доказанным.
Для малого числа наблюдений (n£30) степень надежности коэффициента корреляции может определяться по специальной таблице. При этом число наблюдений таблицы К (число степеней свободе n ) равно числу наблюдений в исследовании без двух, т.е. К = n-2. Как правило, коэффициент корреляции рассчитывается при числе коррелируемых пар не менее 5.
В медицинских и биологических исследованиях связь между признаками считается статистически значимой, если величина коэффициента корреляции больше или равна табличной при Р=0,05
Показатели оценки коэффициента корреляции при малом числе наблюдений
|
K |
P |
|||
|
0,1 |
0,05 |
0,02 |
0,01 |
|
|
1 |
0,988 |
0,997 |
0,9995 |
0,99988 |
|
2 |
900 |
950 |
980 |
990 |
|
3 |
800 |
878 |
934 |
959 |
|
4 |
729 |
811 |
882 |
917 |
|
5 |
669 |
754 |
883 |
874 |
|
6 |
662 |
707 |
789 |
834 |
|
7 |
582 |
666 |
750 |
798 |
|
8 |
549 |
632 |
716 |
765 |
|
9 |
521 |
602 |
685 |
735 |
|
10 |
497 |
576 |
658 |
708 |
|
11 |
476 |
532 |
634 |
684 |
|
12 |
458 |
532 |
612 |
661 |
|
13 |
441 |
514 |
592 |
641 |
|
14 |
426 |
497 |
574 |
623 |
|
15 |
412 |
482 |
558 |
606 |
|
16 |
400 |
468 |
542 |
590 |
|
17 |
389 |
456 |
528 |
575 |
|
18 |
378 |
444 |
516 |
561 |
|
19 |
369 |
433 |
503 |
549 |
|
20 |
360 |
423 |
492 |
537 |
|
25 |
323 |
381 |
445 |
487 |
|
30 |
296 |
349 |
409 |
449 |
|
35 |
275 |
325 |
381 |
418 |
|
40 |
257 |
304 |
358 |
393 |
|
45 |
243 |
288 |
338 |
354 |
|
50 |
231 |
273 |
322 |
354 |
|
60 |
211 |
250 |
295 |
325 |
|
70 |
195 |
232 |
274 |
302 |
|
80 |
183 |
217 |
256 |
283 |
|
90 |
173 |
205 |
242 |
267 |
|
100 |
164 |
195 |
230 |
254 |
Пример. В районах изучалась зависимость между охватом населения прививками и уровнем заболеваемости. Полученный коэффициент корреляции по этим двум признакам был равен 0,81. Число наблюдений – 8 районов (пар), следовательно, К равно 6 (8-2). По таблице находим строку 6 и сравниваем полученный коэффициент. При данном числе степеней свободы (К) коэффициент корреляции превышает табличный для вероятности Р=0,05 (графа 3). Отсюда с вероятностью, большей, чем 95%, можно утверждать, что зависимость между охватом населения прививками и заболеваемостью не случайна, и эта связь сильная, т.е. чем больше процент привитых, тем меньше уровень заболеваемости.
Проверка гипотезы о значимости парного коэффициента корреляции.
Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости парного коэффициента корреляции между результативной переменной у и факторной переменной х.
Основная гипотеза состоит в предположении о незначимости парного коэффициента корреляции, т. е.
Н0:rxy=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости парного коэффициента корреляции, т. е.
Н1:rxy
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
При проверке значимости парного коэффициента корреляции критическое значение t-критерия определяется как tкрит(a;n-h), где а – уровень значимости, (n-h) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.
При проверке основной гипотезы вида Н0:rxy=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

где ryx – выборочный парный коэффициент корреляции между результативной переменной у и факторной переменной х, который рассчитывается по формуле:

(ryx) – величина стандартной ошибки парного выборочного коэффициента корреляции.
Показатель стандартной ошибки парного выборочного коэффициента корреляции для линейной модели парной регрессии рассчитывается по формуле:

Если данное выражение подставить в формулу для расчёта наблюдаемого значения t-критерия для проверки гипотезы вида Н0:rxy=0, то получим:

При проверке основной гипотезы возможны следующие ситуации:
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е.
tнабл|>tкрит, то с вероятностью (1-а) или
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|еляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.
Применение t-статистики Стьюдента для проверки гипотезы вида Н0:rxy=0 основано на выполнении двух условий:
1) если объём выборочной совокупности достаточно велик (n
2) коэффициент корреляции по модулю значительно меньше единицы:
0,45
В том случае, если модуль парного выборочного коэффициента корреляции близок к единице, то гипотеза вида Н0:rxy=0 также может быть проверена с помощью z-статистики. Данный метод оценки значимости парного коэффициента корреляции был предложенР. Фишером.
Между величиной z и парным выборочным коэффициентом корреляции существует отношение вида:

В связи с тем, что величина z является нормально распределённой величиной, то проверка основной гипотезы о незначимости парного коэффициента корреляции сводится к провреке основной гипотезы о незначимости величины z:
Н0:z=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости величины z, т. е.
Н1:z
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.
Критическое значение критерия tкрит определяют по таблице нормального распределения (z-распределения) с доверительной вероятностью
При проверке основной гипотезы вида Н0:z=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

где
Показатель стандартной ошибки величины z для линейной модели парной регрессии рассчитывается по формуле:

При проверке основной гипотезы возможны следующие ситуации:
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|>tкрит, то с вероятностью (1-а) или
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|еляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.
Средняя ошибка аппроксимации.
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. ![]() и
и![]() . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:
. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

Существует и другая формула определения средней ошибки аппроксимации:
 , где
, где ![]() .
.
Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.
ГБОУ ВПО
Рязанский государственный Медицинский университет имени академика Павлова
Министерства здравоохранения и социального развития РФ.
Кафедра математики, информатики и медицинской статистики.
Реферат
Коэффициент парной корреляции.
Выполнила:
Студентка 1 курса медико-профилактического факультета 2группы Гордиенко О.Г
Проверила:
Назарова О.А.
Рязань,2012
StudFiles.ru
/ ТСШ Корреляция
n =10
=10
10а0+52а1=100
52а0+356,24а1=702,44
а0=-1,024; а1=2,12

Линейный коэффициент корреляции может принимать значения от -1 до +1
Если r отрицательна – это обратная зависимость между х и у, т.е. с увеличением х уменьшается у и наоборот.
Если r =0 – связь отсутствует между х и у
Если 0 < r < 1 – связь функциональная.
Оценка надежности коэффициента корреляции и коэффициента регрессии
Коэффициент корреляции можно рассчитать и по выборочным данным. В этом случае должна быть рассчитана ошибка коэффициента корреляции μr.
Если n > 50, то этот показатель определяется по формуле ![]() , а сам коэффициент корреляции – в пределах r±3μr.
, а сам коэффициент корреляции – в пределах r±3μr.
Если nr.
1. Если ![]() , то r считается значимым, а связь реальной.
, то r считается значимым, а связь реальной.
2. Если ![]() ,то связь между у и х недоказана, то можно высказать предположение, что значение коэффициента корреляции, отличное от 0, получено случайно.
,то связь между у и х недоказана, то можно высказать предположение, что значение коэффициента корреляции, отличное от 0, получено случайно.
Аналогично определяется и ошибка корреляционного отношения и его значимость. Необходимо отметить, что при различных значениях отобранных единиц в выборочную совокупность, параметры уравнения регрессии также различны.
Следовательно, в каждом конкретном случае, найдя по эмпирическим данным параметры уравнения регрессии, необходимо определить их возможные ошибки и пределы, в которых эти параметры могут находиться, а также определить значимость (существенность) этих параметров.
Рассмотрим ![]() .
.
Средняя ошибка (μ) параметра а0 рассчитывается по формуле:
![]()
где ![]()
(n-2) – число степеней свободы.
![]() можно найти из правила сложения дисперсий
можно найти из правила сложения дисперсий ![]()
Разделим обе части уравнения на общую дисперсию

Средняя ошибка параметра а1

Зная среднюю ошибку параметра и задавшись определенной вероятностью, а следовательно, и коэффициентом доверия (t), можно построить, для каждого параметра доверительные интервалы.
Для коэффициента регрессии:![]()
Значимость (существенность) коэффициента регрессии проверяется путем сопоставления самого параметра (а1), с его средней ошибкой
![]()
По значению t в зависимости от объема наблюдений следят о значимости параметра.
Для n>20, если t>3, параметры считаются значимыми.
Для n
Если tфакт.табл., то параметры считаются значимыми.
Для а1=2,12 средняя ошибка будет равна 
При уровне значимости d=0,05, k=10-2=8, tтабл.=2,306
Т.к. фактически t>табличного, то можно сделать вывод о значимости коэффициента регрессии а1.
Коэффициенты корреляции рангов
Наряду с r и η для измерения тесноты зависимости между коррелируемыми показателями часто используются так называемые эмпирические показатели, которые называются коэффициентом корреляции рангов:
1. Коэффициент Спирмэна (p)
2. Коэффициент Кендэла (τ)
Оба эти показателя основаны на корреляции не самих значений (х и у), а их рангов.
Коэффициент корреляции рангов Спирмэна
Для расчета коэффициентов корреляции рангов Спирмэна значения случайных величин х и у нумеруются (каждое отдельно) в порядке возрастания (или убывания) от 1 до n, т.е. им присваивается определенный ранг (Nх и Nу) – порядковый номер в ряду. Если встречается несколько одинаковых значений х (или у), то каждому значению присваивается ранг, равный частному от деления суммы рангов, приходящихся на эти значения, на число этих равных значений.
Затем ранги отдельных значений факторного признака сопоставляются с рангами результативного признака.
Разность рангов (Nx-Ny) обозначают d. Степень тесноты связи между изучаемыми признаками в этом случае можно определить по формуле Спирмэна
![]()
где d – разность рангов х и у
n – число пар наблюдений.
Коэффициент корреляции рангов Спирмэна р находится в пределах от 0 до ±1. Когда ранги результативного признака полностью совпадают с рангами факторного признака, то каждое значение Nx=Ny и ∑d2=0, тогда р = 1, то можно говорить о почти полной прямой связи. Если ранги идут строго в противоположном направлении, т.е. первому рангу фактора х соответствует n-й ранг (последний) результативного признака у, второму рангу х соответствует n-1 ранг у и т.д., то в этом случае максимальная величина будет равна

может иметь максимальное значение 2.
И тогда по формуле Спирмэна р=-1, что свидетельствует почти о полной обратной связи между х и у.
Если же связь между изменениями х и у отсутствует (р=0), то очевидно, в этом случае должно наблюдаться равенство.
![]()
Этот показатель менее точен по сравнению с r и η. Расчет показателя прост, поэтому ему отдают предпочтение.
Пример.
|
производственные основные фонды, млн.р. х |
валовая продукция, млн.р у |
Nx |
Ny |
d=Nx-Ny |
d2 |
|
60,5 |
836,4 |
11 |
10,5 |
0,5 |
0,25 |
|
40,7 |
836,4 |
10 |
10,5 |
-0,5 |
0,25 |
|
33,8 |
303,0 |
7 |
9 |
-2 |
4 |
|
22,1 |
134,9 |
4 |
1,5 |
2,5 |
6,25 |
|
33,8 |
139,3 |
7 |
3 |
4 |
16 |
|
33,8 |
265,0 |
7 |
7 |
0 |
0 |
|
20,9 |
181 |
1,5 |
4 |
-2,5 |
6,25 |
|
35,9 |
287,2 |
9 |
8 |
1 |
1 |
|
21,6 |
189,9 |
3 |
5,5 |
-2,5 |
6,25 |
|
22,4 |
189,9 |
5 |
5,5 |
-0,5 |
0,25 |
|
20,9 |
134,9 |
1,5 |
1,5 |
0 |
0 |
|
∑ |
40,5 |
Находим коэффициент Спирмэна ![]()
Зависимость между стоимостью основных фондов и выпускаемой продукции сильная.
Коэффициент Кендэла (τ)
Для расчета значения ранжируются. Затем определяют меру соотношения последовательности рангов у последовательности рангов х.
При этом для каждого ранга у определяют число следующих за ним значений рангов, превышающих его величину. Сумму чисел таких превышений обозначаем Р и будем считать со знаком (+). Аналогично для каждого ранга (у) определяют число следующих за ним рангов, имеющих значение меньше его величины. Сумма чисел таких случаев обозначаем через Q и будем считать со знаком (-).
Очевидно, что Р достигает максимума в том случае, если ранги у точно совпадают с рангами х. Если число пар рангов равно n, то максимальное значение слагаемого Р будет равно:
Рmax=(n-1)+(n-2)+…+3+2+1=n(n-1)/2
Соответственно слагаемое Qmax тоже имеет максимум абсолютного значения,
если последовательность вариантов у имеет обратную тенденцию по отношению к последовательности рангов вариантов х.
![]()
Коэффициент Кендэла (τ) предполагает измерение меры соот-ия последовательности рангов двух переменных путем сравнения общего итога ∑ положительных и отрицательных баллов (S=P+Q) с максимальным значением одного из слагаемых, т. е. ![]()
Пример:
|
Производ. фонды, млн.р. х |
валовая продукция, млн.р. у |
Nx |
Ny |
d=Nx-Ny |
d2 |
|
1,2 |
2,8 |
1 |
1 |
0 |
0 |
|
1,6 |
4,0 |
2 |
3 |
-1 |
1 |
|
2,5 |
3,8 |
3 |
2 |
1 |
1 |
|
3,8 |
6,5 |
4 |
4 |
0 |
0 |
|
4,3 |
8,0 |
5 |
5 |
0 |
0 |
|
5,5 |
10,1 |
6 |
7 |
-1 |
1 |
|
6,0 |
9,5 |
7 |
6 |
1 |
1 |
|
8,0 |
12,5 |
8 |
8 |
0 |
0 |
|
9,1 |
18,3 |
9 |
9 |
0 |
0 |
|
10,0 |
24,5 |
10 |
10 |
0 |
0 |
|
n=10 |
4 |
![]()
Рассчитаем коэффициент Кендэла
у: Р= 9+7+7+6+5+3+3+2+1=43
х: Q=0+(-1)+0+0+0+(-1)+0+0+0=-2
S=43-2=41
Тогда ![]()
Получаемый коэффициент свидетельствует о значительной тесноте зависимости между изменениями значений х и у.
Данная формула применима для тех случаев, когда отдельные значения признака (х и у) не повторяются и следовательно, их ранги не объединены.
Коэффициент Фехнера
Он строится на сравнении поведения отклонений отдельных вариантов от своей средней величины по каждому признаку. При этом принимается во внимание не величина самих отклонений, а их знаки. Найдя отклонение от средней в каждом ряду, сравнивают знаки и досчитывают число совпадений и несовпадений знаков.
Если совпадения знаков обозначить символом С, а несовпадения – Н, то коэффициент Фехнера можно записать как ![]()
|
х |
у |
|
|
|
1,2 |
2,8 |
- |
- |
|
1,6 |
4,0 |
- |
- |
|
2,5 |
3,8 |
- |
- |
|
3,8 |
6,5 |
- |
- |
|
4,3 |
8,0 |
- |
- |
|
5,5 |
10,1 |
+ |
+ |
|
6,0 |
9,5 |
+ |
- |
|
8,0 |
12,5 |
+ |
+ |
|
9,1 |
18,3 |
+ |
+ |
|
10,0 |
24,5 |
+ |
+ |
|
|
|
![]()
Число совпадений 9, число несовпадений 1.
Применение корреляционно-регрессивного анализа связи
Рассмотрим влияние вариации факторного показателя х на результативный у.
Пример.
Имеется следующая информация по однотипным предприятиям о возрасте (продолжительности эксплуатации) силового оборудования и затратах на его ремонт.
|
№ предприятия |
возраст оборудования, лет. |
затраты на ремонт, т.р. |
|
1 |
4 |
1,5 |
|
2 |
5 |
2,0 |
|
3 |
5 |
1,4 |
|
4 |
6 |
2,3 |
|
5 |
8 |
2,7 |
|
6 |
10 |
4,0 |
|
7 |
8 |
2,3 |
|
8 |
7 |
2,5 |
|
9 |
11 |
6,6 |
|
10 |
6 |
1,7 |
В условиях использования ЭВМ выбор адекватной математической функции осуществляется перебором решений наиболее часто применяемых.
Наиболее часто встречается прямолинейная зависимость.
ух=а0+а1х
Для определения параметров уравнения

Расчетная таблица.
|
№ |
у |
х |
х2 |
ху |
|
1 |
1,5 |
4 |
16 |
6 |
|
2 |
2,0 |
5 |
25 |
10 |
|
3 |
1,4 |
5 |
25 |
7 |
|
4 |
2,3 |
6 |
36 |
13,8 |
|
5 |
2,7 |
8 |
64 |
21,6 |
|
6 |
4,0 |
10 |
100 |
40 |
|
7 |
2,3 |
8 |
64 |
18,4 |
|
8 |
2,5 |
7 |
49 |
17,5 |
|
9 |
6,6 |
11 |
121 |
72,6 |
|
10 |
1,7 |
6 |
36 |
10,2 |
|
∑ |
27 |
70 |
536 |
217,1 |
а0=(27*536-217,1*70)/(10*536-70*70)=-1,576
а1=(10*217,1-70*27)/460=0,611
Зависимость расходов на ремонт от возраста оборудования.
ух=-1,576+0,611х
Проверим эту формулу на типичность:

Для определения ![]() на основе формулы определяем выравненные значения ухi
на основе формулы определяем выравненные значения ухi
ух1=-1,576+0,611*4=0,868
ух2,3=-1,576+0,611*5=1,479
ух4,10=-1,576+0,611*6=2,09
ух5,7=-1,576+0,611*8=3,312
ух6=-1,576+0,611*10=4,534
ух8=-1,576+0,611*7=2,701
ух9=-1,576+0,611*11=5,145
Расчетная таблица
|
№ |
у |
х |
ух |
у-ух |
(у-ух)2 |
|
( |
у2 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
1,5 |
4 |
0,868 |
0,632 |
0,399 |
-3 |
9 |
2,25 |
|
2 |
2,0 |
5 |
1,479 |
0,521 |
0,271 |
-2 |
4 |
4,0 |
|
3 |
1,4 |
5 |
1,479 |
-0,079 |
0,006 |
-2 |
4 |
1,96 |
|
4 |
2,3 |
6 |
2,09 |
0,21 |
0,044 |
-1 |
1 |
5,29 |
|
5 |
2,7 |
8 |
3,312 |
-0,612 |
0,374 |
1 |
1 |
7,29 |
|
6 |
4,0 |
10 |
4,534 |
-0,534 |
0,285 |
3 |
9 |
16,0 |
|
7 |
2,3 |
8 |
3,312 |
-1,012 |
1,024 |
1 |
1 |
5,29 |
|
8 |
2,5 |
7 |
2,701 |
-0,201 |
0,040 |
0 |
0 |
6,25 |
|
9 |
6,6 |
11 |
5,145 |
1,455 |
2,117 |
4 |
16 |
43,56 |
|
10 |
1,7 |
6 |
2,09 |
-0,39 |
0,152 |
1 |
1 |
2,89 |
|
∑ |
27 |
70 |
27,01 |
х |
4,712 |
х |
46 |
94,78 |

В экономико-статистических исследованиях принято, что уровень значимости а=0,05 и число степеней свободы k=10-2, то табличное критическое значение tk= 5,32.
Сравнение фактических и табличных значений t-критерия
ta0>tka1
Это позволяет признать вычисленные по уравнению параметры типичными.

Полученная величина R=0,756 означает, что в соответствии со шкалой Чеддока установленная по уравнению регрессии связь между затратами на ремонт и возрастом оборудования высокая.
Оценка значимости коэффициента корреляции осуществляется по t-критерию. Фактическое значение этого критерия

При критическом значении tk=2,3 получается, что tr>tk. Вычисленный коэффициент корреляции признается существенным.
Множественная (многофакторная) регрессия
Изучение связи между тремя и более связанными между собой признаками носит название множественной регрессии. Задача состоит в определении аналитического выражения связи между результативным признаком (у) и факторным признаками (х1,х2,х3…хn) .
![]()
Построение моделей множественной регрессии включает несколько этапов:
- выбор формы связи (уравнение регрессии)
- отбор факторных признаков
- обеспечение достаточного объема совокупности для получения несмещенных оценок.
Рассмотрим каждый из них:
1. Выбор формы связи.
Наиболее применимый способ – это метод перебора различных уравнений. Сущность метода заключается в том, что большое число уравнений, отобранных для описания связи какого-либо социально-экономического явления или процесса, реализованного на ЭВМ с помощью специально разработанных программ перебора с последующей статистической проверкой на основе t-критерия Стьюдента и F-критерия Фехнера – Снедекора. Этот способ очень трудоемкий. Практика построения многофакторных моделей показывает, что все реально существующие зависимости между социально-экономическими явлениями можно описать 5 типами моделей.
1. Линейная
![]() 1,2…n=a0+a1x1+a2x2+…+anxn
1,2…n=a0+a1x1+a2x2+…+anxn
StudFiles.ru
Коэффициент корреляции
Две случайные величины х и у находятся в корреляционной зависимости, если изменение одной из величин влечет за собой изменение закона распределения другой. Для характеристики зависимости между случайными величинами вводят понятие корреляционного момента или ковариации. Корреляционным моментом случайной величины х и у называется математическое ожидание произведения отклонений этих величин от их математических ожиданий
Корреляционные зависимости
 ,
,
Для дискретной случайной величины (отношение) ковариация вычисляется
 (1)
(1)
 (2)
(2)  (3)
(3)
Для непрерывных случайных величин
 (4)
(4)
 (5)
(5)
 (6)
(6)
Из формулы (4) можно получить более простую формулу.



Получим
 (7)
(7)
Теорема №1 Если случайные величины х и у независимы то их cov(x;y)=0
Доказательство: для непрерывной величины.

в формуле 4 заменим


центральный момент первого порядка равен нулю, следовательно и выражение равно нулю. Для независимых случайных величин необходимо чтобы cov=0, но обратно не верно.
Если ковариация двух случайных величин отлична от нуля - это есть признак зависимости между ними. cov характеризует не только зависимость величинами , но и их рассеивание. Если одна из величин весьма мало отклоняется от своего математического ожидания , то есть почти неслучайно, то cov – будет мала, какой бы тесной зависимостью не были бы связаны эти величины. Поэтому между случайными величинами вводят безразмерный коэффициент корреляции.
Коэффициентом корреляции случайных величин х и у называется отношение их ковариации к произведению средних квадратических отклонений их величин. Корреляция - есть безразмерная величина. Поэтому величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин( в этом состоит преимущество коэффициента перед ковариацией) .
 .
.
Свойства коэффициента корреляции:
1. Коэффициент корреляции независимых случайных величин равен нулю .
Это свойство вытекает из определения коэффициента корреляции . Таким образом, т.к. из независимости случайных величин следует их некоррелированность, то отличие коэффициента корреляции от нуля свидетельствует о наличии зависимости между величинами.
Как же именно коэффициент корреляции характеризует зависимость между случайными величинами?
Оказывается , что коэффициент корреляции является мерой линейной зависимости между величинами ( говорят также , мерой прямолинейности) :показывает , насколько хорошо в среднем может быть представлена каждая из величин в виде линейной функции от другой. Это видно из следующих свойств коэффициента корреляции.
2. Для любых величин 
Доказательство:
 ,
,
 ,
,
 ,
,
 .
.
3. Если коэффициент корреляции положительный, то связь между переменными также положительна и значение переменной увеличивается и уменьшается одновременно.
Если r - имеет отрицательное значение, то при уменьшении одной переменной уменьшаются и другие.
4. Коэффициент корреляции не зависит от выбора начала отсчета и единицы измерения, то есть от любых постоянных а1 b1, а2 b2.
r(а1х+b1;a2x+b2)=r(x;y) a1,a2>0, таким образом переменные х и у можно уменьшать или увеличивать в а-раз, а также вычитать и прибавлять одно и тоже число b, в результате величина коэффициента корреляции не изменяется.
5. Если случайные величины х и у линейно зависимы, т.е. существует между ними соотношения у=ах+b, то |rху|=1
Пример: Дана таблица, закон распределения двумерной случайной величины
| у\х |  , ,  , ,  , , |
||
| 0,12 | 0,18 | 0,1 | |
| 0,1 | 0,11 | 0,39 |
D[x]=M[x2]-M2[x]
Вывод: коэффициент корреляции есть показатель того, насколько связь между случайными величинами близка и строгой линейной зависимости.
Он отмечает и слишком большую долю случайности. Существуют также случайные величины, для которых коэффициент корреляции является достаточно полным показателем зависимости. Сюда относятся в первую очередь величины, между которыми заранее, из общих соображений , можно предсказать линейную зависимость.
Например: измеряя в электрической цепи одновременно напряжение и силу тока, мы ( по закону Ома) должны ожидать между ними линейной зависимости ( пропорциональности) . Поэтому сильное отличие коэффициента корреляции от 1 будет свидетельствовать о недостатках измерительных приборов или о наличии переменного сопротивления в цепи.
Сильно повышается ценность коэффициента корреляции для величин, собственные случайные колебания которых подчиняются нормальному закону. Для таких величин равенство коэффициента корреляции нулю означает отсутствие всякой зависимости.
Последнее свойство особенно важно, т.к. при обработке наблюдений преимущественно сталкиваемся с нормальным распределением.
studopedia.ru
Коэффициент корреляции
Наиболее точный способ определения тесноты и характера корреляционной связи - нахождение коэффициента корреляции. Коэффициент корреляции есть число определяемое по формуле:

где rху— коэффициент корреляции;
xi—значения первого признака;
уi—значения второго признака;
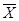 —средняя арифметическая значений первого признака
—средняя арифметическая значений первого признака
 средняя арифметическая значений второго признака
средняя арифметическая значений второго признака
Для пользования формулой (32) построим таблицу, которая обеспечит необходимую последовательность в подготовке чисел для нахождения числителя и знаменателя коэффициента корреляции.
Как видно из формулы (32), последовательность действий такая: находим средние арифметические обоих признаков х и у, находим разность между значениями признака и его средней (хі- 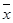 ) и уі-
) и уі-  ), затем находим их произведение (хі-
), затем находим их произведение (хі- 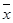 ) (уі-
) (уі-  ) – суммa пocлeдних дает числитель коэффициента корреляции. Для нахождения его знаменателя следует разности (xi—
) – суммa пocлeдних дает числитель коэффициента корреляции. Для нахождения его знаменателя следует разности (xi— 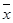 )и (уі -
)и (уі -  ) возвести в квадрат, найти их суммы и извлечь корень квадратный из их произведения.
) возвести в квадрат, найти их суммы и извлечь корень квадратный из их произведения.
Так для примера 31 нахождение коэффициента корреляции в соответствии с формулой (32) можно представить следующим образом (табл. 50).
Полученное число коэффициента корреляции дает возможность установить наличие, тесноту и характер связи.
1. Если коэффициент корреляции равен нулю, связь между признаками отсутствует.
2. Если коэффициент корреляции равен единице, связь между признаками столь велика, что превращается в функциональную.
3. Абсолютная величина коэффициента корреляции не выходит за пределы интервала от нуля до единицы:
0xy|
Это дает возможность ориентироваться на тесноту связи: чем величина коэффициента ближе к нулю, тем связь слабее, а чем ближе к единице, тем связь теснее.
4. Знак коэффициента корреляции «плюс» означает прямую корреляцию, знак «минус»—обратную.
Таблица50
| хі | уі | (хі- 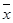 ) ) |
(уі-  ) ) |
(хі- 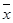 )(уі- )(уі-  ) ) |
(хі- 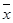 )2 )2 |
(уі-  )2 )2 |
| 14,00 | 12,10 | —1,70 | —2,30 | +3,91 | 2,89 | 5,29 |
| 14,20 | 13,80 | —1,50 | —0,60 | +0,90 | 2,25 | 0,36 |
| 14,90 | 14,20 | —0,80 | —0,20 | +0,16 | 0,64 | 0,04 |
| 15,40 | 13,00 | —0,30 | —1,40 | +0,42 | 0,09 | 1,96 |
| 16,00 | 14,60 | +0,30 | +0,20 | +0,06 | 0,09 | 0,04 |
| 17,20 | 15,90 | +1,50 | +2,25 | 2,25 | ||
| 18,10 | 17,40 | +2,40 | +2,00 | +4,80 | 5,76 | 4,00 |
| 109,80 | 101,00 | 12,50 | 13,97 | 13,94 |
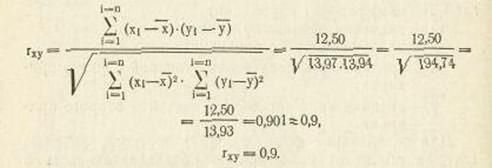
Таким образом, вычисленный в примере 31 коэффициент корреляции rxy = +0,9. позволяет сделать такие выводы: существует корреляционная связь между величиной мышечной силы правой и левой кистей у исследуемых школьников (коэффициент rxy =+0,9 отличен от нуля), связь очень тесная (коэффициент rxy =+0,9 близок к единице), корреляция прямая (коэффициент rxy = +0,9 положителен), т. е. с увеличением мышечной силы одной из кистей увеличивается сила другой кисти.
При вычислении коэффициента корреляции и пользовании его свойствами следует учесть, что выводы дают корректные результаты в том случае, когда признаки распределены нормально и когда рассматривается взаимосвязь между большим количеством значений обоих признаков.
В рассмотренном примере 31 анализированы только 7 значений обоих признаков, что, конечно, недостаточно для подобных исследований. Напоминаем здесь еще раз, что примеры, в данной книге вообще и в этой главе в частности, носят характер иллюстрации методов, а не подробного изложения каких-либо научных экспериментов. Вследствие этого рассмотрено небольшое число значений признаков, измерения округлены — все это делается для того, чтобы громоздкими вычислениями не затемнять идею метода.
Особое внимание следует обратить на существо рассматриваемой взаимосвязи. Коэффициент корреляции не может привести к верным результатам исследования, если анализ взаимосвязи между признаками проводится формально. Возвратимся еще раз к примеру 31. Оба рассмотренных признака представляли собой значения мышечной силы правой и левой кистей. Представим себе, что под признаком xi в примере 31 (14,0; 14,2; 14,9... ...18,1) мы понимает длину случайно пойманных рыб в сантиметрах, а под признаком уі (12,1; 13,8; 14,2... ...17,4) —вес приборов в лаборатории в килограммах. Формально воспользовавшись аппаратом вычислений для нахождения коэффициента корреляции и получив в этом случае также rxy =+0>9, мы должны были заключить, что между длиной рыб и весом приборов существует тесная связь прямого характера. Бессмысленность такого вывода очевидна.
Чтобы избежать формального подхода к пользованию коэффициентом корреляции, следует любым другим методом — математическим, логическим, экспериментальным, теоретическим — выявить возможность существования корреляционной связи между признаками, то есть обнаружить органическое единство признаков. Только после этого можно приступать к пользованию корреляционным анализом и устанавливать величину и характер взаимосвязи.
В математической статистике существует еще понятие множественной корреляции — взаимосвязи между тремя и более признаками. В этих случаях пользуются коэффициентом множественной корреляции, состоящим из парных коэффициентов корреляции, описанных выше.
Например, коэффициент корреляции трех признаков—хі, уі, zі — есть:
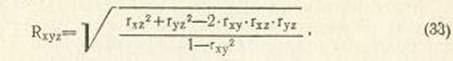
где Rxyz—коэффициент множественной корреляции, выражающий, как признак хi зависит от признаков уі и zi;
rxy —коэффициент корреляции между признаками xi и yi;
rxz—коэффициент корреляции между признаками Xi и Zi;
ryz—коэффициент корреляции между признаками yi, zi
studopedia.ru
Читайте также
![Коэффициент корреляции может принимать значения Коэффициент корреляции может принимать значения]() Коэффициент корреляции может принимать значения
Коэффициент корреляции может принимать значения![Значения коэффициентов корреляции графиков нагрузки потребителей Значения коэффициентов корреляции графиков нагрузки потребителей]() Значения коэффициентов корреляции графиков нагрузки потребителей
Значения коэффициентов корреляции графиков нагрузки потребителей![Значение коэффициента корреляции Значение коэффициента корреляции]() Значение коэффициента корреляции
Значение коэффициента корреляции![Коэффициент абсолютной ликвидности нормативное значение Коэффициент абсолютной ликвидности нормативное значение]() Коэффициент абсолютной ликвидности нормативное значение
Коэффициент абсолютной ликвидности нормативное значение![Корреляция значения Корреляция значения]() Корреляция значения
Корреляция значения![Коэффициент корреляции генеральной совокупности определение Коэффициент корреляции генеральной совокупности определение]() Коэффициент корреляции генеральной совокупности определение
Коэффициент корреляции генеральной совокупности определение![Рекомендуемое значение коэффициента текущей ликвидности Рекомендуемое значение коэффициента текущей ликвидности]() Рекомендуемое значение коэффициента текущей ликвидности
Рекомендуемое значение коэффициента текущей ликвидности![Оптимальное значение коэффициента автономии Оптимальное значение коэффициента автономии]() Оптимальное значение коэффициента автономии
Оптимальное значение коэффициента автономии![Расчет коэффициента детерминации невозможен без значения коэффициента Расчет коэффициента детерминации невозможен без значения коэффициента]() Расчет коэффициента детерминации невозможен без значения коэффициента
Расчет коэффициента детерминации невозможен без значения коэффициента![Коэффициент финансового рычага нормативное значение Коэффициент финансового рычага нормативное значение]() Коэффициент финансового рычага нормативное значение
Коэффициент финансового рычага нормативное значение![Коэффициент финансовой независимости нормативное значение Коэффициент финансовой независимости нормативное значение]() Коэффициент финансовой независимости нормативное значение
Коэффициент финансовой независимости нормативное значение![Коэффициент концентрации привлеченного капитала нормативное значение Коэффициент концентрации привлеченного капитала нормативное значение]() Коэффициент концентрации привлеченного капитала нормативное значение
Коэффициент концентрации привлеченного капитала нормативное значение
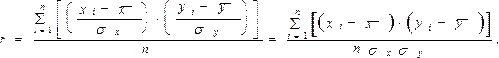 Коэффициент корреляции может принимать значения
Коэффициент корреляции может принимать значения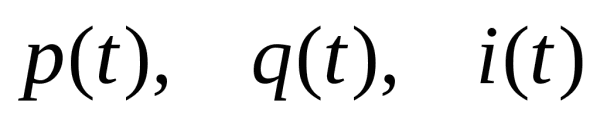 Значения коэффициентов корреляции графиков нагрузки потребителей
Значения коэффициентов корреляции графиков нагрузки потребителей Коэффициент абсолютной ликвидности нормативное значение
Коэффициент абсолютной ликвидности нормативное значение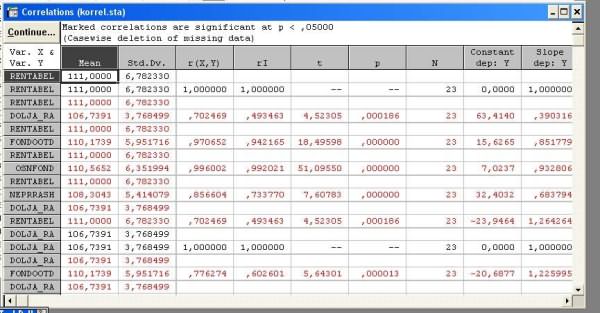 Корреляция значения
Корреляция значения Коэффициент корреляции генеральной совокупности определение
Коэффициент корреляции генеральной совокупности определение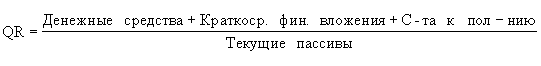 Рекомендуемое значение коэффициента текущей ликвидности
Рекомендуемое значение коэффициента текущей ликвидности Оптимальное значение коэффициента автономии
Оптимальное значение коэффициента автономии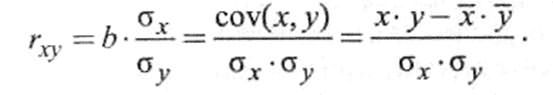 Расчет коэффициента детерминации невозможен без значения коэффициента
Расчет коэффициента детерминации невозможен без значения коэффициента Коэффициент финансового рычага нормативное значение
Коэффициент финансового рычага нормативное значение Коэффициент финансовой независимости нормативное значение
Коэффициент финансовой независимости нормативное значение Коэффициент концентрации привлеченного капитала нормативное значение
Коэффициент концентрации привлеченного капитала нормативное значение